船用挖掘机机械臂刚柔耦合动力学及特性研究

李发宗，童水光，王相兵，程晓民

（1.浙江大学 能源工程学系，杭州 3100271；2.宁波工程学院 机械学院，浙江 宁波 315016）

桁架式船用挖掘机因臂架长、承载大，在回转或变幅过程中易产生变形［1］。对此种挖掘机的动力学研究属刚柔耦合系统动力学范畴。文献［2－5］在机械臂动力学建模、运动学与轨迹规划、动力学及控制取得不少研究成果。然而已有机械臂动力学研究大都基于瞬态结构假设及单独考虑刚体运动与柔性变形，忽略刚柔耦合产生的非线性动力学效应，未考虑柔性变形对整个系统动态特性影响。对类似船用挖掘机机械臂的动力学性能分析均由试验获取，在动力学方程建模、数值求解及仿真分析上仍处于探索阶段［6－8］。计算机仿真横拟及数值求解技术的飞速发展为机械臂进行刚柔耦合动力学分析提供强有力的技术手段。

本文以WDZ600桁架式船用挖掘机为对象，考虑机械臂轴向变形，选里兹基函数RayleighRitz为模态基函数［9］描述机械臂变形模式。用拉格朗日定理［10］建立机械臂刚柔耦合动力学方程，用数值求解方法获得机械臂固有频率与相关参数的变化关系。用NASTRAN、ADAMS等软件建立柔性臂架、柔性变幅绳、柔性抓斗提升钢丝绳、刚性支架、刚性回转平台的船用挖掘机虚拟样机模型并进行仿真分析，获得系统位移、速度、加速度、连接点铰接力及机械臂动态应力等特性。

1 机械臂刚柔耦合多体动力学建模

1.1 机械臂机构系统广义坐标系建立

船用挖掘机WDZ600由双足支架装置、平台系统、回转机构及动臂系统等组成。通过回转机构、提升机构及变幅机构配合实现回转、提升、变幅等动作进行物料转移。臂架采用桁架结构形式，由4根方钢主弦、多条角钢腹杆等焊接而成，分臂头、顶节、标准节、底节四部分，承担主要载荷。变幅系统可通过调整变幅钢丝绳长度改变臂架仰角实现。机械臂系统通过回转支承及平台与船体连接实现回转运动。船用挖掘机工作装置部件三维装配见图1。据图1建立臂架系统机构广义坐标系见图2。为方便分析，选船用挖掘机机械臂与回转工作平台联接铰点为坐标原点建立惯性坐标系。建立机械臂大范围刚性转动的坐标系1∑1O1x1y1；坐标原点O1同O0。坐标平面x1O1y1与平面xoy重合，xl轴与 x轴成 θ（θf1）角。选广义坐标 qf＝［θf1qf2qf3］T，θf1、qf2、qf3分别表示点 O1处转角、点 B沿 x向位移、点 B沿y向位移（挠度），R为柔性梁任一点P在动坐标系∑1O1x1y1下位移；N为变幅钢丝绳与双足支架铰点。选柔性机械臂模态基函数为

图1 船用挖掘机工作装置三维装配组成Fig.1 Dimensional assembly constitute of marine excavator’s working device

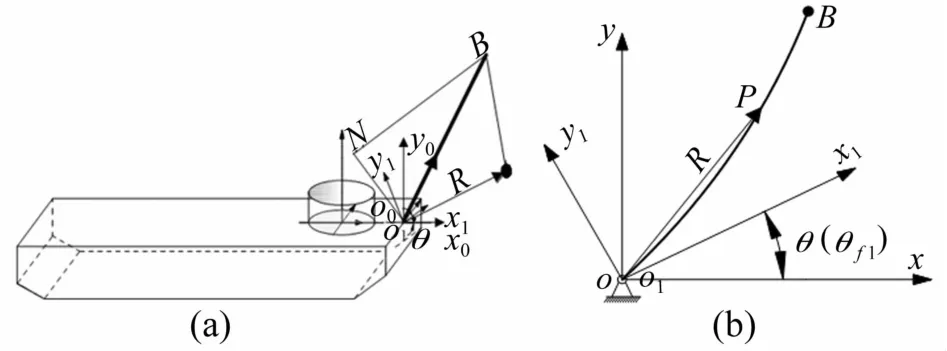
图2 大型船用挖掘机臂架系统机构广义坐标系Fig.2 Generalized coordinate system of large marine excavator’s boom mechanism

为能准确表示大范围刚性转动的悬臂梁任一点弹性位移，引入耦合项wc，令耦合基函数为c，在小变形条件下，c为

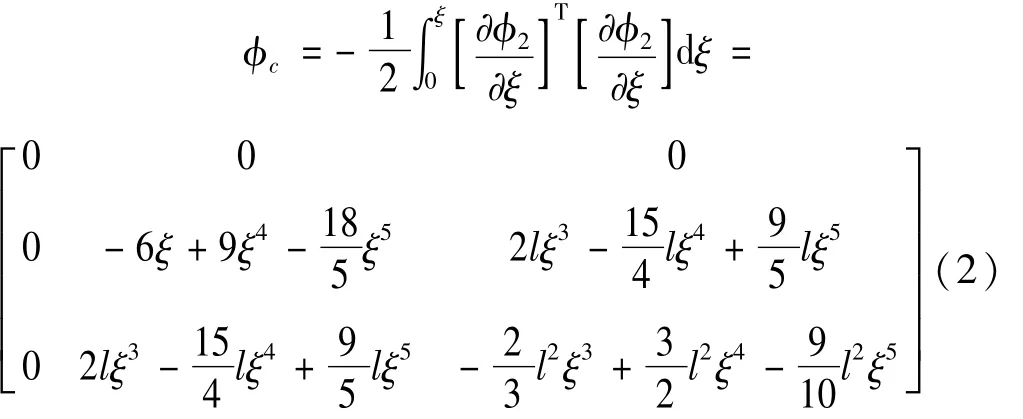
1.2 船用液压挖掘机臂系统动力学控制方程

忽略阻尼C，据拉格朗日乘子法（Lagrange）机构约束方程为

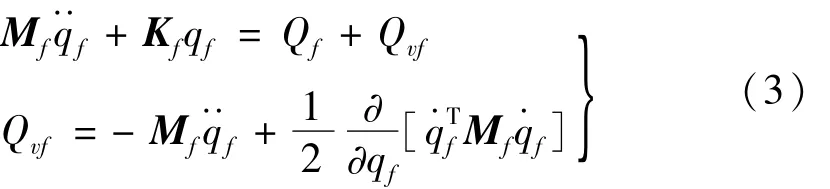
式中：Qvf为由速度二次项对应的广义力弹性分量；Qf为广义外力对应的弹性分量；Mf为机构质量矩阵；Kf为刚度矩阵。

1.2.1 质量矩阵确定

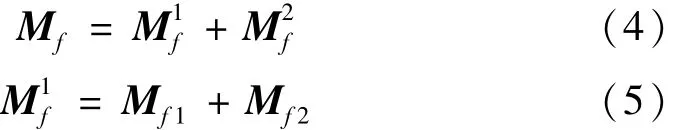
式中：为机械臂广义弹性质量矩阵；为未端集中质量广义弹性质量矩阵；为不考虑耦合变形的弹性质量矩阵；为耦合变形贡献的弹性质量矩阵。各表达式为

同理，末端集中质量广义弹性质量矩阵为

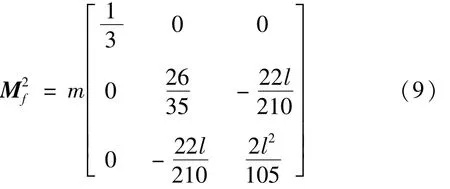
柔性梁机械臂系统质量矩阵为

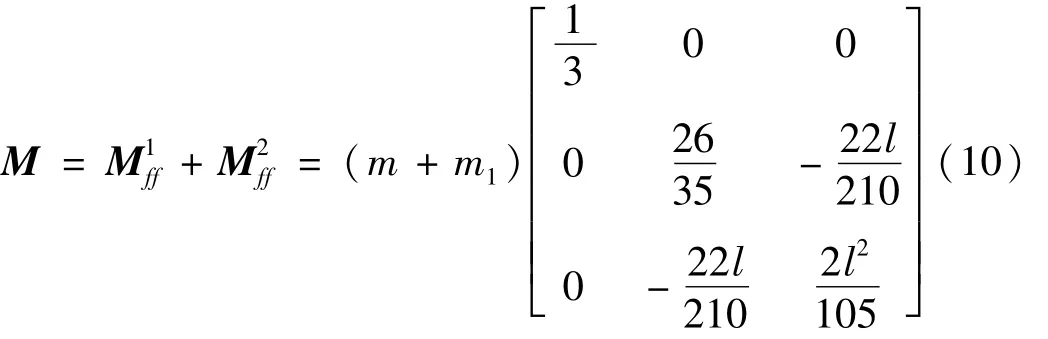
1.2.2 刚度矩阵确定

机械臂刚度矩阵由两部分组成，即

式中：Kf为弹性刚度矩阵；Kd为大范围运动产生的动力刚度矩阵。

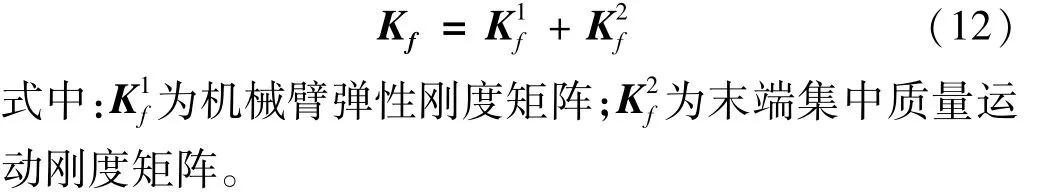
机械臂弹性刚度矩阵可通过相对动坐标系的弹性变形势能求得

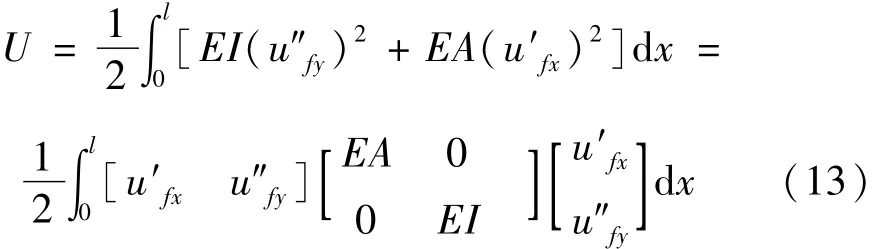
式中：uy为机械臂中性轴横向位移；ux为机械臂中性轴轴向位移。

机械臂末端质量贡献刚度矩阵为

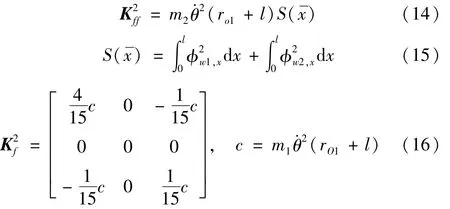
式中：Sx）为耦合形函数；ro1为机械臂基座铰点至变幅卷筒中心距离。

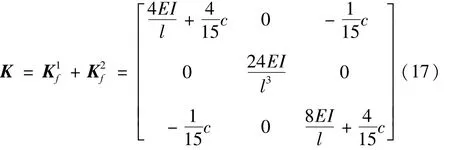
1.2.3 广义力列阵确定

式（3）中Qvf与悬臂梁转动角速度·θ有关，从相对运动动力学角度看，相当于离心惯性力与科氏惯性力，即

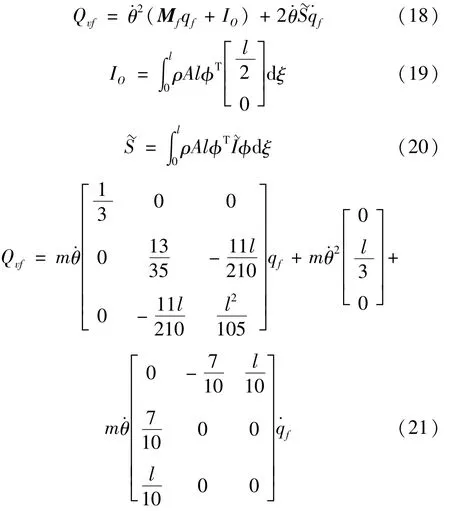
式中：IO为机械臂转动惯量；S槇为单元形函数。

求解式（3）中Qf与臂架及抓斗重力Qf1及钢丝绳内力 Qf2，即

式中：lt为t时刻钢丝绳长度；rD为点O至点C的位移矢量为点B在动坐标系1下变形及未变形位移矢量；为点C在动坐标系1下位移矢量；N为点B所在单元变形函数。

钢丝绳内力虚功δWe为

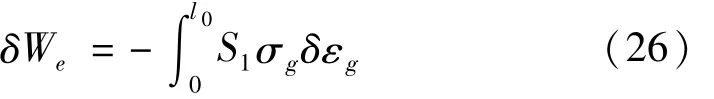
式中：S1为钢丝绳截面积；σg为钢丝绳应力。

钢丝绳广义内力列阵为

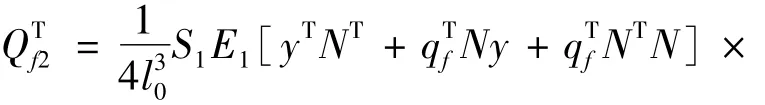
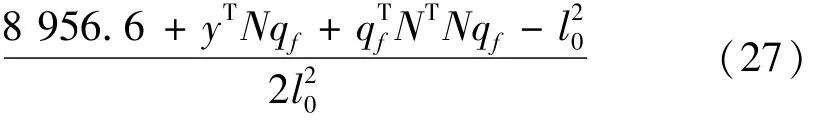
式中：E1为钢丝绳弹性模量。

2 工作装置机械臂动力学数值求解

船用挖掘机机械臂动特性能参数对结构参数的灵敏度矩阵表达式［11－13］为

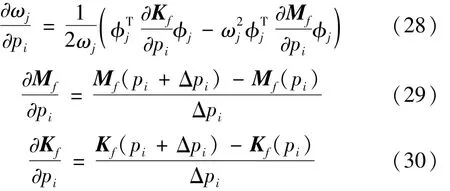
式中：ωj为相关部件第 j阶固有频率；j为第 j阶固有振型。

由式（30）知，模态频率对性能参数灵敏度与质量、阻尼、刚度矩阵灵敏度及振动速度、激励频率、结构物理参数相关。WDZ600型船用挖掘机机械臂长l＝23 m，平均质量m＝480 kg／m，弹性模量 E＝2.0×1011N／m2，截面惯性矩 S＝0.055 6 m4，机械臂绕定轴转动最大角速度·θ＝0.36 rad·s－1。据式（10）、（17）动力学方程系数矩阵及式（27）～式（29），利用MATLAB编程进行数值求解得相关几何参数的一阶固有频率灵敏度。B处沿X、Y向振动固有频率值随机械臂转动角速度变化曲线见图3、图4。由两图看出，B处沿yl方向振动固有频率随机械臂绕O1转动角速度增加略有增大，考虑数量级为10－4，可忽略；B处沿xl方向振动固有频率基本无变化。

忽略式（4）、（10）中 Mf2，Kf，即不考虑刚柔耦合所得机械臂刚体运动的固有频率关系，得B处沿X、Y向振动固有频率值随机械臂长度变化曲线见图5、图6。由两图看出，机械臂绕O1转动、B处沿xl方向振动固有频率随机械臂长度增加略有增大，而B处沿yl方向振动固有频率呈下降趋势，且考虑刚柔耦合运动后所得机械臂振动固有频率低。

图3 机械臂在B处沿X向振动频率随角速度变化曲线Fig.3 Relation curve of mechanical arm vibration frequency changed with angular velocity along with X direction at B point

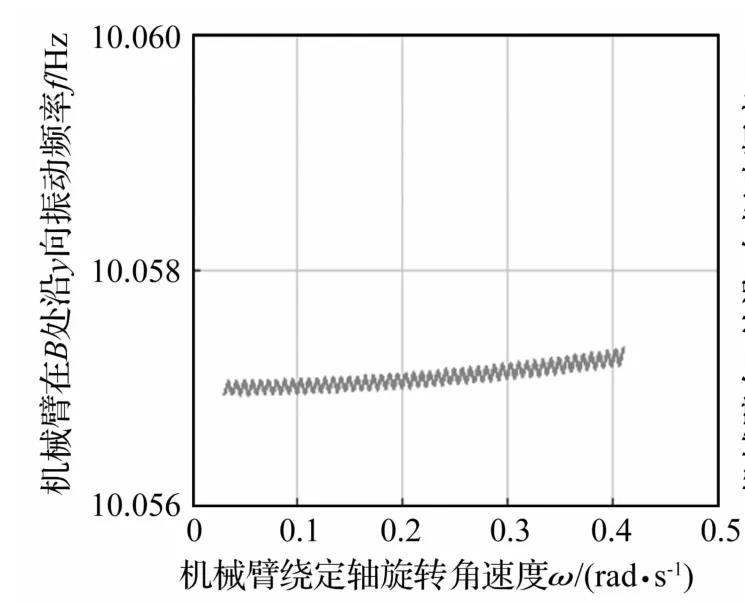
图4 机械臂在B处沿Y向振动频率随角速度变化曲线Fig.4 Relation curve of mechanical arm vibration frequency changed with angular velocity along with Y direction at B point

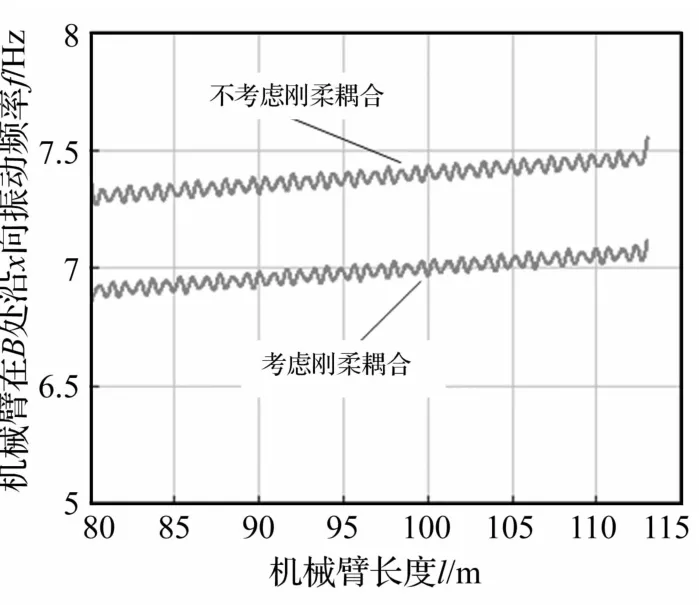
图5 机械臂在B处沿X向振动频率随机械臂长变化曲线Fig.5 Relation of vibration frequency along with X direction at B point changed with the arm length for the mechanical arm

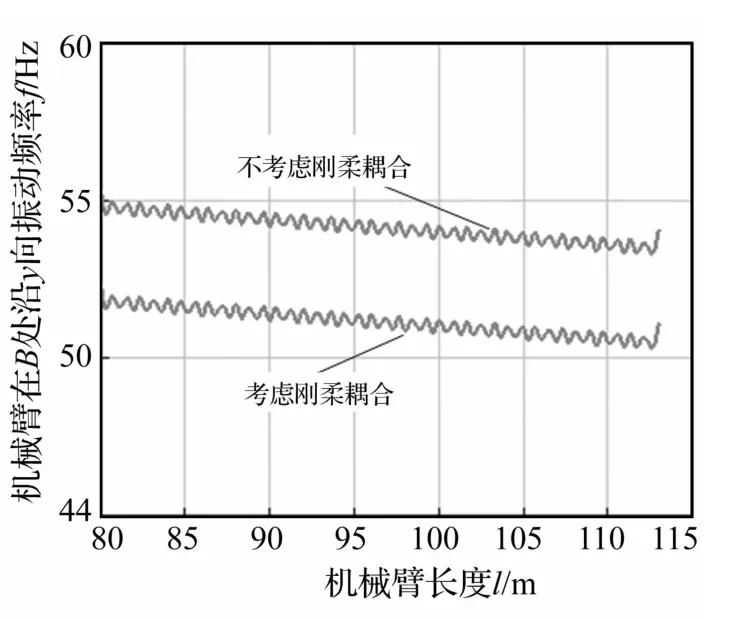
图6 机械臂在B处沿Y向振动频率随机械臂长变化曲线Fig.6 Relation of vibration frequency alongwith Y direction at B point changed with the arm lengthfor the mechanical arm

3 船用挖掘机机械臂刚柔耦合动力学仿真

WDZ600型船用液压挖掘机工作装置机械臂的刚柔耦合动力学仿真过程为：在UG中建立船用挖掘机工作装置动臂、回转支承、平台、双足支架三维实体模型。调出 Parasolid（.x＿t或.x＿b文件）格式文件导入 ADAMS中进行位置调整，保证装配正确［14］。在ADAMS中相应空间位置建立32个圆柱体小段，小段间用bushing轴套力连接，设置刚度、阻尼系数，完成钢丝绳建模。对臂架柔性体进行模态分析，生成柔性体模态中性文件.mnf，该文件含柔性体质量、质心、转动惯量、频率、振型及对载荷的参与因子等信息。将.mnf文件导入ADAMS中替换相应刚性体，建立船用挖掘机工作装置刚柔耦合虚拟样机模型见图7。船用挖掘机动臂柔性体模态分析结果见图8。

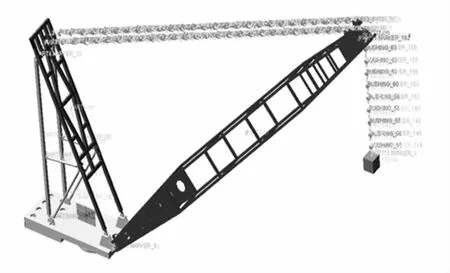
图7 船用控掘机刚柔耦合虚拟样机模型Fig.7 Rigid coupling virtual prototype model of marine excavator’s moving arm

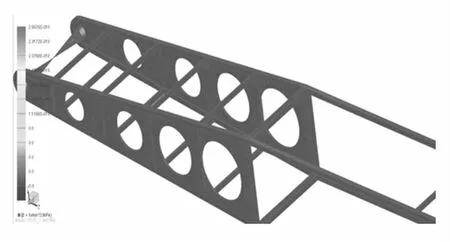
图8 船用挖掘机动臂柔性体模态分析结果Fig.8 Flexible body modal analysis results of marine excavator’s moving arm

3.1 起臂工况仿真

在起臂工况仿真过程中分别对臂架底节与中间节连接处、臂架重心处、顶节与中间节连接处三个较危险位置上弦杆进行分析，得各处应力曲线。图9表示起臂过程中不同臂节重心处应力变化曲线，不同起臂速度时主臂重心处应力曲线见图10。由图9看出，应力最大值出现在起臂初始阶段，且随主臂仰角增加而减小。主臂重心处应力400 MPa明显高于其它位置处应力，底节与中间节连接处应力最小172 MPa。因此对重心处应力进行重点分析。对起臂速度分别为15 mm／s、25 mm／s、60 mm／s时主臂重心处应力进行分析，由图10看出，应力最大值随起臂速度增加而增加。速度突变时应力值出现峰值；设定速度变化时间大于10 s时，应力峰值会小于不变速时应力峰值。因此，可通过适当改变起臂速度改进臂架受力，以保证较高的起臂效率。

3.2 突然卸载工况仿真

研究挖掘机在突然卸载 0.125 s、0.25 s、0.375 s时的动态特性，对比分析挖掘机动态响应值卸载后的时间历程中动态响应最大值，即加载点1的X、Y方向位移、速度、加速度、单根变幅拉索拉力及臂架顶节点动态应力。不同时间历程下动态响应分析结果见图11～图14。不同卸载时间各动力学响应最大值对比见表1。

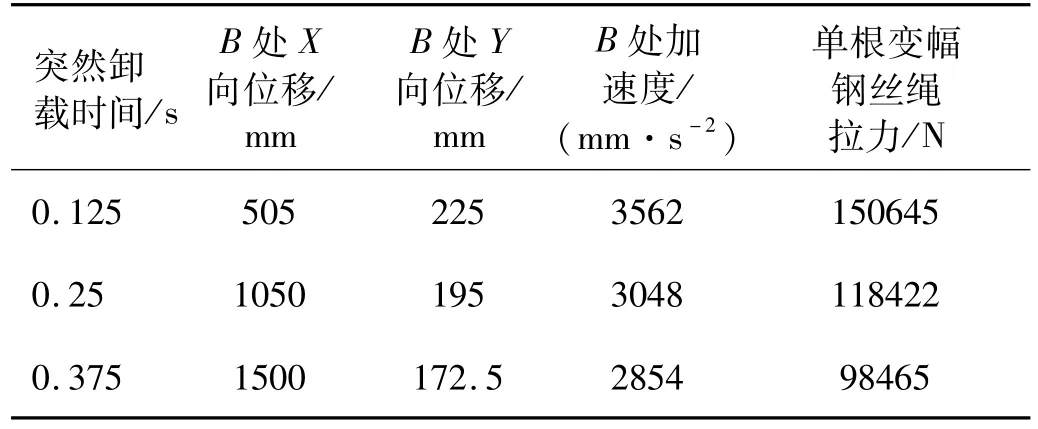
表1 不同卸载时间各动力学响应最大值对比Tab.1 Maximum comparison of each dynamicresponse valuefor the different unloading time

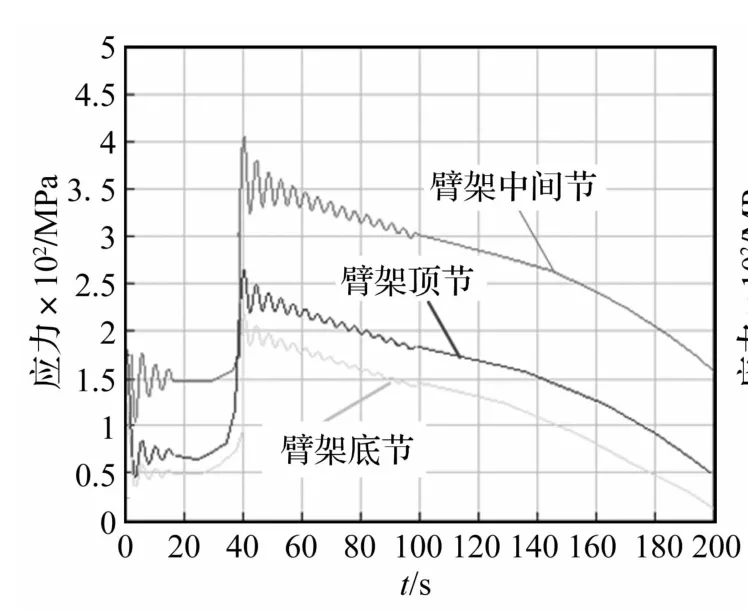
图9 起臂过程中不同臂节重心处应力变化曲线Fig.9 Variable spline of stress at the center of boom gravity at different arm sections during rising boom

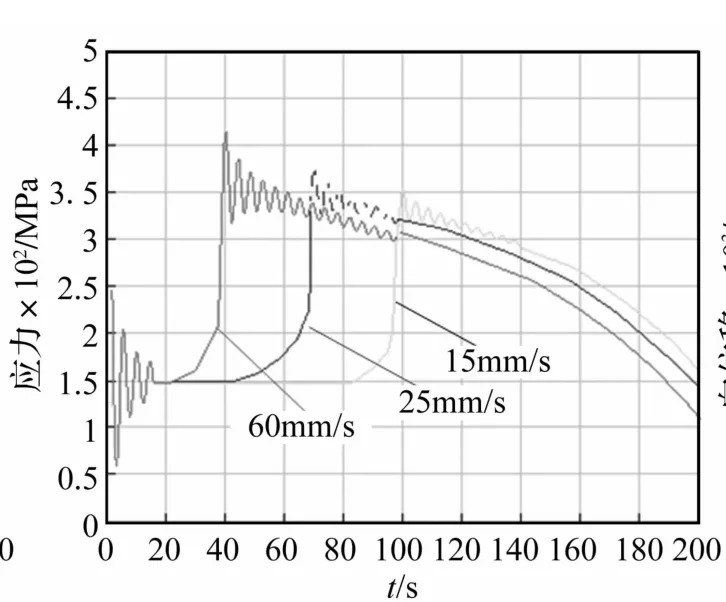
图10 不同起臂速度时臂架主臂处应力曲线Fig.10 Spline of stress during rising boom at main arm during the different boom rising speed

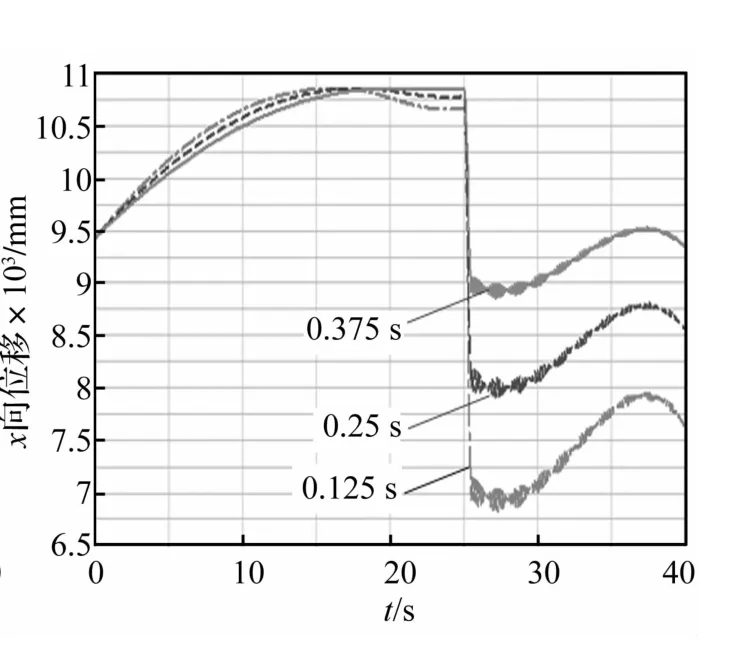
图11 突然卸载不同时间历程B处X方向位移曲线Fig.11 X direction displacement curve at B point suddenly unstallingduringthe different time course

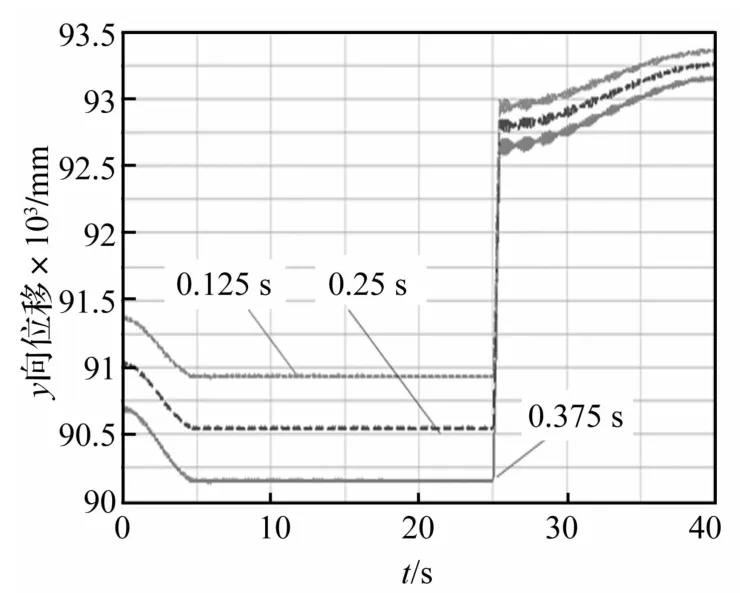
图12 突然卸载不同时间历程B处Y向位移曲线Fig.12 Y direction displacement curve at B point suddenly unstallingduringthe different time course

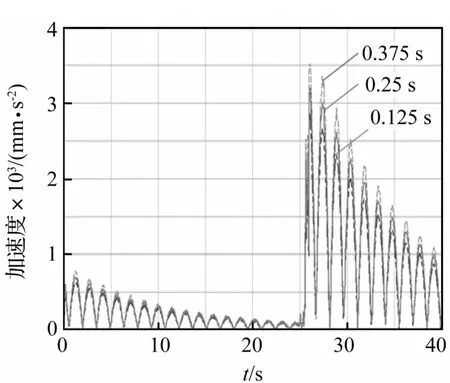
图13 突然卸载不同时间历程B处加速度曲线Fig.13 Acceleration curve at B point suddenly unstalling during the different time course

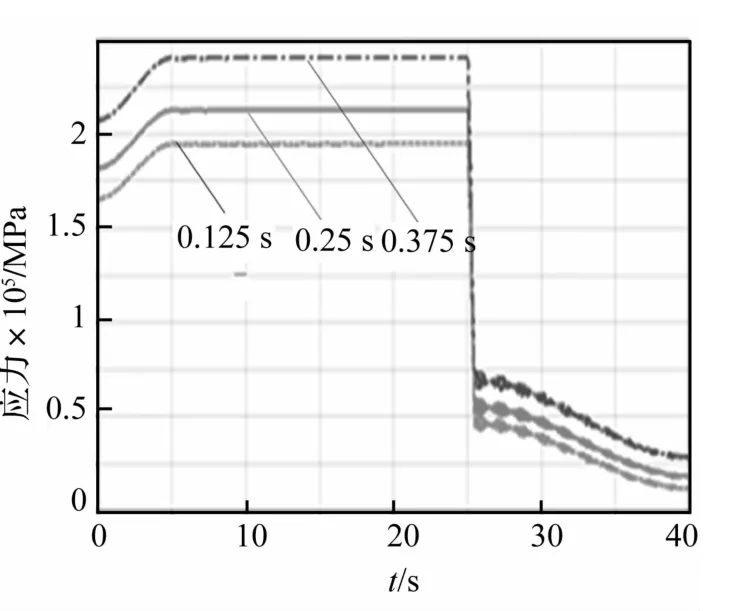
图14 突然卸载不同时间历程变幅钢丝绳拉力曲线Fig.14 Pullup curve of luffing rope suddenly unstalling during the different time course

对比仿真结果知，随卸载时间增加节点应力值、加载点位移值、速度及加速度值、变幅钢丝绳内力及动臂与平台的铰接力均减小。突然卸载时间延长能显著减少对整机瞬间冲击作用，改善动臂振动情况，降低动应力，变幅钢丝绳受力显著减少，降低损耗。因此，在大型船用挖掘机抓斗卸载物料过程中，在保证工作效率前提下，适当延长物料卸载时间可提高挖掘机的动态性能。

4 结果对比论证

4.1 固有频率特性的结果比较

利用上节臂架柔性体的模态中性文件中的有限元结果文件，将臂架长度依次设为23 m、20 m、17 m分别进行有限元模态计算，并与数值求解分析结果对比，见表2。由表2看出，有限元分析与数值结果较接近，从而验证刚柔耦合动力学理论建模的正确性。

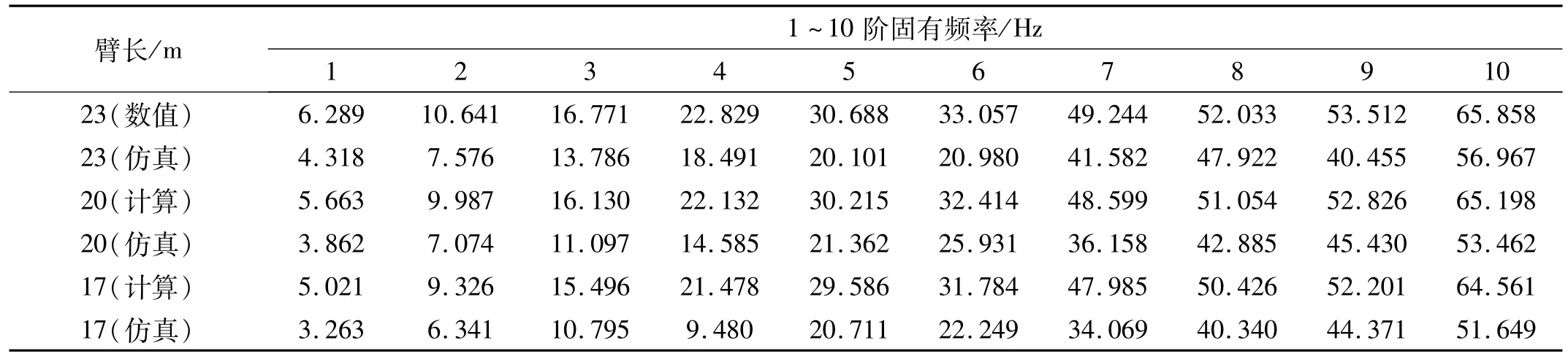
表2 机械臂1～10阶固有频率数值与仿真结果对比（Hz）Tab.2 Natural frequency comparison of numerical solution and simulation solution for mechanical arm

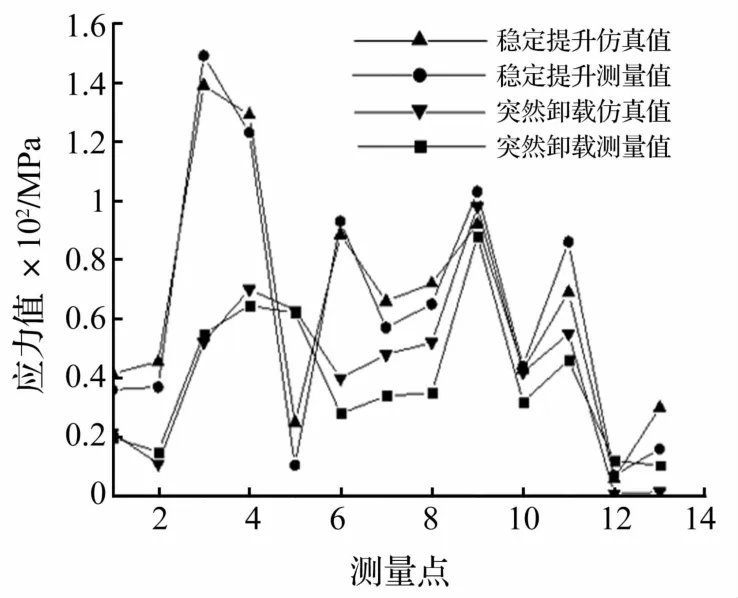
图15 测试值与计算值对比Fig.15 Comparison of test and calculated values

4.2 动力学特性实验验证

采用与动力学仿真相同工况，结合实际经验，对臂架顶端至底端在不同臂节连接处、各臂节中心处及其它危险点共13处进行应力测试。13处应力测试结果与计算值对比见图15。由图15看出，稳定提升时最大应力为139.44 MPa，位于上臂架顶端外侧第3测点。实验值与计算值大小及变化趋势基本一致，误差在8%以内。突然卸载时最大应力测量值为83.12 MPa，位于缓冲杆附近第7测点，计算值88.71 MPa，误差6.33%，其余测点误差均在10%以内。

对船用挖掘机工作过程中臂架变形最大位移用视频图像测量技术［15］进行测量。测试用摄像机分辨率1 280×720，拍摄速率30帧／s，利用Matlab软件处理所得水平、竖直方向位移时间图，测点突然卸载后的最大位移为ΔX＝92 mm，ΔY＝157 mm，与仿真值误差在15%以内。通过应力、位移测试并与臂架刚柔耦合仿真结果对比知，仿真模型的准确性获得验证。

5 结 论

基于柔性梁多体理论对船用挖掘机机械臂的运动过程分析推导建立动力学微分方程，用数值求解方法获得机械臂振动固有频率与相关参数的变化关系。应用NASTRAN、ADAMS等软件对船用挖掘机机械臂机构进行刚柔耦合动力学仿真，获得典型工况的动力学响应曲线，并进行动力学特性分析，结论如下：

（1）由于刚柔耦合特性，船用挖掘机机械臂刚柔耦合动力学方程的质量、刚度矩阵高度耦合。

（2）由于机械臂刚柔耦合运动影响，计算结果较用结构动力学方法忽略刚柔耦合作用所得结果固有频率值低。

（3）通过动力学方程的数值求解及仿真分析，可研究影响机械臂结构动力学特性影响因素，发现结构薄弱环节，提出改进意见。

（4）建模及分析方法可为进一步研究船用挖掘机工作装置机械臂虚拟样机模型及运动的精确控制提供依据。

［1］杨辉.刚－柔耦合动力学系统的建模理论与实验研究［D］.上海：上海交通大学，2002.

［2］Basher H A.Modeling and simulation of flexible robot manipulator with a prismatic joint［C］.Proceedings，IEEE Southeast Con，2007.

［3］刘杰，戴丽，赵丽娟，等.混凝土泵车臂架柔性多体动力学建模与仿真［J］.机械工程学报，2007，43（1）：131－134.LIU Jie，DAI Li，ZHAO Lijuan，et al.Modeling and simulation of flexible multibody dynamics of concrete pump truck arm［J］.Chinese Journal of Mechanical Engineering，2007，43（1）：131－134.

［4］宋建龙.柔性机械臂动力学建模与仿真研究［D］.天津：天津大学，2001.

［5］Leung A Y T，Wu G Z，Zhong W F.Nonlinear dynamic analysis of flexible multibody system［J］.Acta Mechanica Solida Sinica，2004，17（4）：330－336.

［6］黎业飞，邱清盈，冯培恩.基于刚柔混合建模的时变结构动力学分析［J］.浙江大学学报（工学版），2007，16（2）：311－314.LI Yefei，QIU Qingying，FENG Peien.Dynamicanalysis of timevarying structure based on rigidflexible hybrid modeling［J］.Journal of Zhejiang University（Engineering Science），2007，16（2）：311－314.

［7］杨为，王家序，秦大同.液压挖掘机工作装置固有频率的试验灵敏度［J］.农业机械学报，2006，37（2）：21－24.YANG Wei，WANG Jiaxu，QIN Datong.Investigation on experimental sensitivity of work device natural frequency of hydraulic excavator［J］.Transactions of the Chinese Society for Agricultural Machinery，2006，37（2）：21－24.

［8］He Qinghua，Ghang Daqing，Hao Peng，et al.Modeling and control of hydraulic excavator＇s arm［J］.Journal of Central South University of Technology，2006，13（4）：422－427.

［9］徐彦，刘杰，孙光复，等.刚柔耦合运动对起重机吊臂振动固有频率的影响［J］.机械工程学报，2006，42（8）：142－145.XU Yan，LIU Jie，SUN Guangfu，et al.Influence of rigid bodyand deformation couplingonthe vibrating natural frequencies of the boomina crane［J］.Chinese Journal of Mechanical Engineering，2006，42（8）：142－145.

［10］王相兵，童水光.基于刚柔耦合的液压挖掘机机械臂非线性动力学研究［J］.振动与冲击，2014，33（1）：63－70.WANG Xiangbing，TONG Shuiguang.Nonlinear dynamical behavior analysis for rigidflexible coupling［J］.Journal ofVabration and Shock，2014，33（1）：63－70.

［11］唐冕.大跨度自锚式悬索桥的静动力性能研究与参数敏感性分析［D］.长沙：中南大学，2007：46－49.

［12］张令弥，何柏庆，袁向荣.设计灵敏度分析的迭代模态法［J］.南京航空航天大学学报，1994，26（3）：320－321.ZHANG Lingmi，HE Baiqing，YUAN Xiangrong.Interative modal method for sensitivity analysis of design parameters［J］. Journal of Nanjing University of Aeronautics＆Astronautics，1994，26（3）：320－321.

［13］Jones K，Turcotte J.Finite element model updating using antiresonant frequencies［J］.Journal of Sound and Vibration，2002，252（4）：717－727.

［14］丁国富.液压挖掘机虚拟样机的实现方法和技术研究［D］.杭州：浙江大学，2001.

［15］李玲，涂熙，王磊，等.桁梁局部破断实验中动位移的数字图像测量［J］.结构工程师，2010（1）：113－117.LI Ling，TU Xi，WANG Lei，et al.Digital image processing technique for dyamic displacement in trussbeam local failure test［J］.Structural Engineerings，2010（1）：113－117.