列车－桥梁－汽车耦合振动仿真分析

陈上有，路 萍，刘 高，夏 禾

（1.中交公路规划设计院有限公司，北京 100088；2.中交公路长大桥建设国家工程研究中心有限公司，北京 100088；3.中交水运规划设计院有限公司，北京 100007；4.北京交通大学 土木建筑工程学院，北京 100044）

随铁路的高速化、重载化，对列车与桥梁动力相互作用已有大量研究，建立不同的力学分析模型，研究成果已用于工程实践［1－8］。而特大跨径公路桥的车－桥耦合振动颇受关注，尤其强风作用的汽车－桥梁耦合振动研究较多［9－11］。针对跨江、河公轨、公铁两用桥梁，已开展跨座式轻轨车与汽车同时作用的公轨两用特大桥梁动力响应及行车舒适性研究［12－13］。而进行公铁两用桥梁的车－桥耦合振动仿真分析时，汽车通常采用静轴重加载计及其影响［14］，将汽车视为动力子系统的文献极少［15］。显然，考虑汽车与桥梁的动力耦合效应更符合实际，利于准确评价列车、汽车的运行安全性及舒适性。

基于此，本文视汽车为动力子系统，同时考虑列车子系统与桥梁子系统、汽车子系统与桥梁子系统间的相互作用，建立列车－桥梁－汽车耦合振动分析模型，推导系统运动方程，编制仿真分析软件，并用该软件对某公铁两用桥进行列车－桥梁－汽车耦合振动仿真分析。为公铁（轨）两用桥梁车－桥耦合振动仿真分析提供借鉴。

1 列车－桥梁－汽车耦合系统

1.1 列车车辆模型

二系悬挂的单节车辆模型由1个车体、2台转向架、4个轮对组成。每个车体有横摆Yc、沉浮Zc、侧滚θc、点头φc及摇头ψc5个自由度；每台转向架有横摆Yt、沉浮 Zt、侧滚 θt、点头 φt及摇头 ψt5个自由度；每个轮对有横摆Yw、沉浮Zw、侧滚θw及摇头ψw4个自由度。车体与前后转向架之间、转向架与各轮对之间由线性弹簧及粘滞阻尼器相连。单节车辆动力分析模型见图1。列车子系统运动方程可表示为

式中：Mc，Cc，Kc，Xc分别为列车子系统总体质量、阻尼、刚度矩阵及位移向量；Fc为列车子系统所受外力向量。

由于忽略各节车间相互作用力，上述各动力矩阵可由各节车辆的动力矩阵以对角线排列方式组成。单节车辆质量、阻尼、刚度矩阵可据Lagrange方程求得。

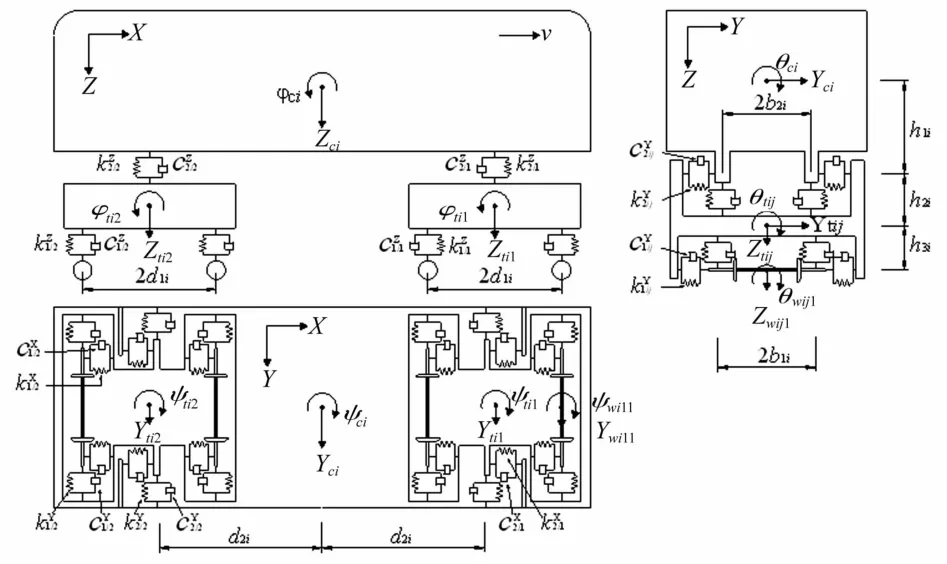
图1 列车车辆动力模型Fig.1 Dynamic model of train vehicle

1.2 汽车车辆模型

汽车车辆通常有三轴六轮及两轴四轮。三轴车辆动力分析模型由1个车体与6个车轮组成，见图2。车体有横摆 Yv、沉浮 Zv、侧滚 θv、摇头 ψv及点头 φv5个自由度，每个车轮有横摆Ys、沉浮Zs2个自由度。两轴四轮车辆可在三轴六轮车辆基础上通过删去多余自由度获得。

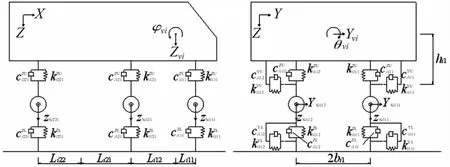
图2 汽车车辆动力模型Fig.2 Dynamic model of road vehicle

汽车子系统运动方程可表示为

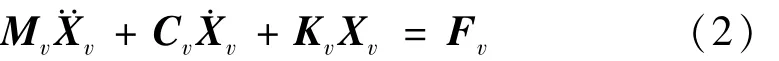
式中：Mv，Cv，Kv，Xv分别为汽车子系统的总体质量、矩阵、刚度矩阵及位移向量；Fv为汽车子系统所受外力向量。

由于各汽车车辆间无相互作用，各动力矩阵可由各车辆的动力矩阵以对角线排列方式组成。单辆汽车车辆质量、阻尼、刚度矩阵可据Lagrange方程求得。

1.3 桥梁有限元模型

桥梁采用有限单元方法模拟，桥梁子系统动力方程可表示为

式中：Mb，Cb，Kb，Xb分别为桥梁子系统的总体质量、阻尼、刚度矩阵及位移向量；Fb为桥梁子系统所受外力向量。

1.4 轨道不平顺与桥梁不平顺

轨道不平顺为轨道左、右轨中心点与理论位置的距离。轨道不平顺作为系统激励输入可按轨道不平顺谱模拟的随机函数，也可据实测轨道不平顺值。桥面不平顺也是如此。本文轨道、桥面不平顺值按不平顺谱用谐波合成法模拟生成。

1.5 列车车辆轮轨接触模型

轮轨间竖向作用力由密贴理论确定，横向作用力由Kalker蠕滑理论确定，轮轨间相互作用力作用于左右轮轨接触点。轮轨间相互作用关系见图3。

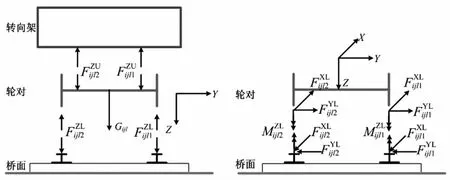
图3 轮轨间相互作用关系Fig.3 Wheelrail interaction diagram

由轮轨位移协调关系，轮轴中心竖向位移Zbcijl及轮轴扭转角θbcijl与桥梁子系统位移关系表示为

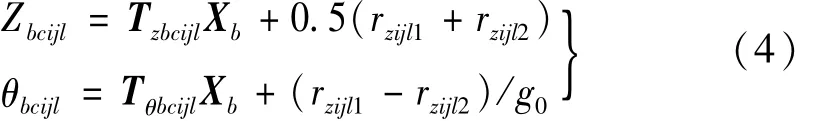
式中：下标ijlk表示第i节车第j个转向架第l个轮对第k（k＝1或2，1表示右、2表示左）侧（下同）；下标 c表示列车；下标b表示桥梁（下同）；rzijl1，rzijl2为右、左接触点处轨道不平顺；Tz，Tθ为桥梁竖向、扭转位移对应的形函数向量；g0为轨距。

据轮对受力平衡，轮轨间竖向作用力FZijlIk及轮对、转向架之间的竖向作用力FZijlUk关系可表示为

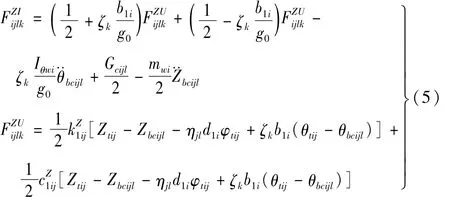
式中：d1为车辆轴矩之半；b1为一系悬挂横向跨矩之半；ηjl为轮对位置函数（ηj1＝1，ηj2＝－1）；ζk为接触点位置函数（ζ1＝1，ζ2＝－1）；mw，Iθw为轮对质量及质量惯性矩；Gc为静轮重；k1Zij，c1Z

ij分别为一系悬挂竖向弹簧刚度及阻尼。

式中：f11，f22，f23，f33为蠕滑系数；v为列车运行速度；Y·bcijl为轮轨左右接触点位置桥梁横向速度附加不平顺变化速度。

为提高模型求解效率，设：① 轮轨接触点处轮对踏面为1∶20的圆锥面，轮轨接触点在轨头区域，此区域钢轨为半径300 mm圆柱体［16］；② 以静轴重作为轮轨间法向力确定蠕滑系数［17］。据上述假设，蠕滑系数对给定半径的轮对而言为常数，此时车－桥耦合系统可处理为线性系统。此简化对桥梁动力学分析影响不大。由于无法考虑轮轨间可能的动态脱离，会影响极端工况下列车轮重减载率、脱轨系数等安全性指标，应引起注意。

1.6 汽车车辆与桥面接触模型

设汽车车轮与公路桥面间为点接触且不分离，则该接触点的横向位移Ybvijlk及竖向位移Zbvijlk与桥梁子系统位移关系可表示为

式中：T为桥梁位移形函数向量；rYijlk为桥面不平顺；下标Y，Z代表横向、竖向。

汽车车轮与桥面间相互作用力可表示为

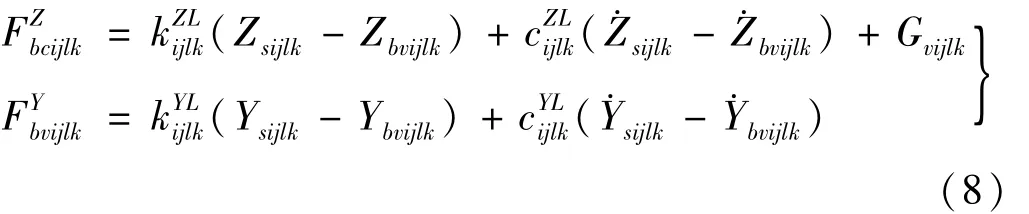
式中，，为轮胎与路面接触的竖向、横向弹性系数及阻尼；Gv为汽车车轮静轴重。

1.7 列车－桥梁－汽车耦合运动方程及数值求解

将列车、桥梁及汽车子系统运动方程联立，可得列车－桥梁－汽车耦合运动方程。为方便求解，据各子系统间相互作用关系删去非独立自由度，并将力向量中含车辆或桥梁动力响应项移至方程左边，右端力向量只保留与轨道、桥面不平顺及车辆、桥梁常参数相关项，推导得列车－桥梁－汽车耦合运动方程为

式中：cc，vv，bb表示列车、汽车、桥梁子系统自相关部分；cb或bc表示列车与桥梁子系统相互影响部分；vb或bv表示汽车与桥梁子系统相互影响部分。限于篇幅，不再给出各子矩阵详细表达式。

列车、汽车过桥过程中随车辆位置的改变，式（9）左端质量、刚度、阻尼矩阵随时间发生变化，式（9）为线性时变系数的二阶微分方程组，可用Newmark－β积分法求解。

1.8 公铁两用桥梁车桥耦合振动分析软件

基于上述分析模型及运动方程，编制仿真分析软件VBI模拟单一车种、多车种车－桥耦合振动。该软件可进行多条线路、不同数目及车型的车队在不同车速及不同桥面、轨道不平顺下的多工况车－桥耦合振动仿真分析计算。

2 计算分析

2.1 某公路铁路两用桥方案

某公、铁两用桥方案为双塔三索面斜拉桥，主跨504 m，上层为6车道公路，下层为4线铁路。斜拉桥主梁为板桁结合钢桁梁。有限元建模中钢桁梁、主塔、边墩及辅助墩用空间梁单元模拟，斜拉索用空间杆单元模拟，正交异性板或结合板用梁格法等效成纵横梁用空间梁单元模拟。共6 268个节点，11 147个单元，自由度总数37 506，见图4。

图4 某公铁两用桥方案有限元模型Fig.4 Finite element model of the bridge

用VBI进行桥梁模态分析，结果与商业软件Ansys结果完全吻合，前5阶振型、频率见表1。

2.2 计算工况

考虑列车与汽车同时上桥运行模式。列车编组为1节ICE机车＋14节高速车辆＋1节ICE机车；汽车用两轴重车模型，20辆车为一车队，按10 m等间距布置。本文计算的4种车辆运行工况，列车速度为250 km／h，汽车速度为80 km／h。

（1）单线列车＋单线汽车（SCSV）。单线列车在铁路轨道L2行驶，单线汽车在公路桥面行车道R2与列车同向行驶，见图5，其中L为左行车道，R为右行车道。

表1 大桥自振频率及振型特点Tab.1 Natural frequencies of the bridge

图5 列车、汽车行驶工况示意图Fig.5 Running condition

（2）单线列车＋双线汽车（SCDV）。单线列车在铁路轨道L2行驶，双线汽车分别在公路桥面行车道R2、R3与列车同向行驶。

（3）双线列车＋单线汽车（DCSV）。双线列车在铁路轨道L1、L2对开行驶，单线汽车在公路桥面行车道R2从左向右行驶。

（4）双线列车＋双线汽车（DCDV）。双线列车在铁路轨道L1、L2对开行驶，双线汽车在公路桥面行车道R2、R3自左向右同向行驶。

2.3 计算结果及分析

利用VBI软件对公铁两用桥方案4种工况下列车－桥梁－汽车耦合振动进行分析。轨道不平顺谱用德国高速铁路低干扰轨道谱，桥面不平顺谱用国际化标准协会的 ISO SCI／WC 4标准［11］。桥梁系统阻尼按Rayleigh阻尼考虑，阻尼比取0.005。积分时间步长为0.05 s。部分系统动力响应时程结果见图6～图9。

4种工况下主跨跨中横向竖向位移及加速度最大值、主塔塔顶纵向横向位移及加速度最大值、列车（机车及车辆）竖向横向加速度及运行安全性以及舒适性指标（脱轨系数、轮重减载率、轮轨横向作用力最大值、舒适度指标SPRING）、汽车车体竖向加速度最大值见表2。由表2看出，4种工况的桥梁考察点纵、横及竖向位移均较小，横、竖向加速度均小于0.5 g。说明桥梁总体竖、横向刚度较大。上桥车队增多时，竖向位移明显增加，原因为竖向位移主要由重力加载引起，而跨中横向位移变化不明显，因横向位移由横向不平顺随机激励引起。机车、车辆横、竖向加速度较小，机车、车辆的Spring指标、脱轨系数、轮重减载率、轮轨横向力均较小，说明车辆运行平稳性好，列车运行安全。汽车横、竖向加速度最大值小于3 m／s2，车辆运行较平稳，说明大桥整体刚度较大。分析中所得轮重减载率、脱轨系数的极值较小，说明轮轨间未发生脱离，所用轮轨接触模型合适。特别指出，对特大型公铁两用桥梁而言，更准确、可靠的列车过桥安全性评价需建立更完备的系统动力学模型，分析各种可能的运营工况，确保桥梁行车安全。

图6 主梁跨中挠度时程Fig.6 Vertical displacement histories of bridge girder

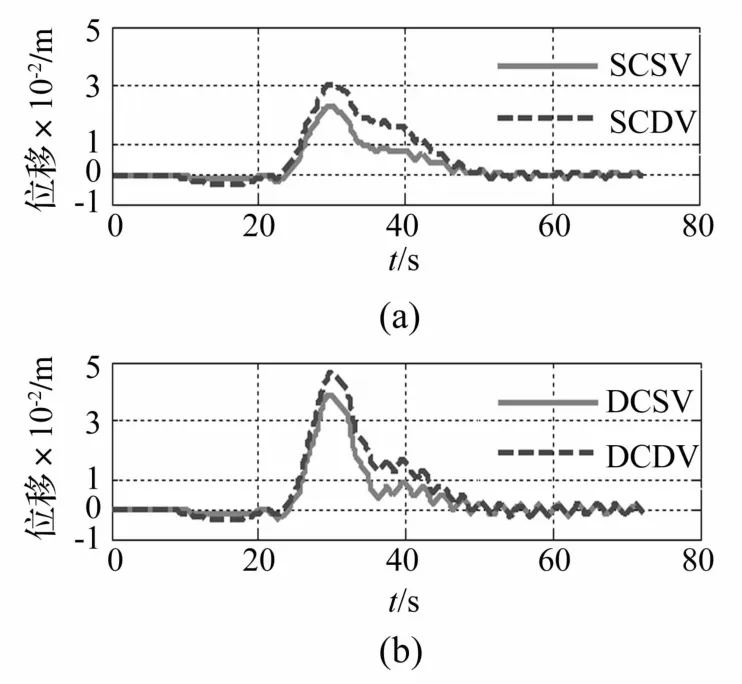
图7 塔顶纵向位移时程Fig.7 Longitudinal displacement histories of bridge tower

随桥上汽车车队增多（SCDV与SCSV比较，DCSV与DSDV比较），列车机车与车辆的竖向加速度最大值、脱轨系数最大值、轮重减载率最大值明显增大，说明汽车车辆过桥对列车运行安全性具有不利影响。列车与汽车同时过桥时，汽车动力所致桥梁振动对列车而言，相当于附加特殊的不平顺激励，列车对此较敏感，等同于运行路况更差。

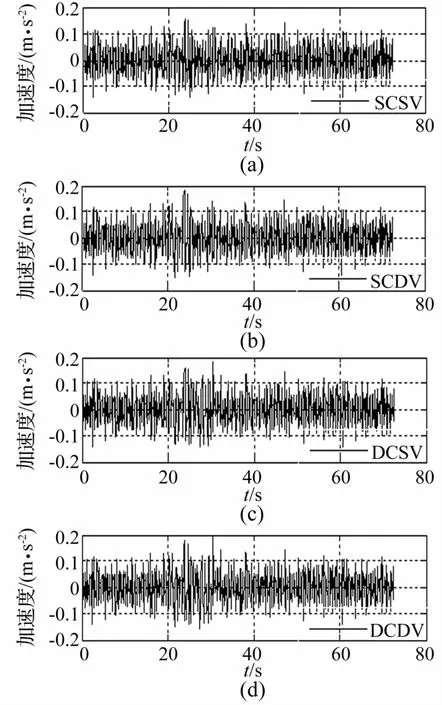
图8 轨道L2列车机车竖向加速度时程Fig.8 Vertical carbody acceleration time histories of the locomotive on L2 railway

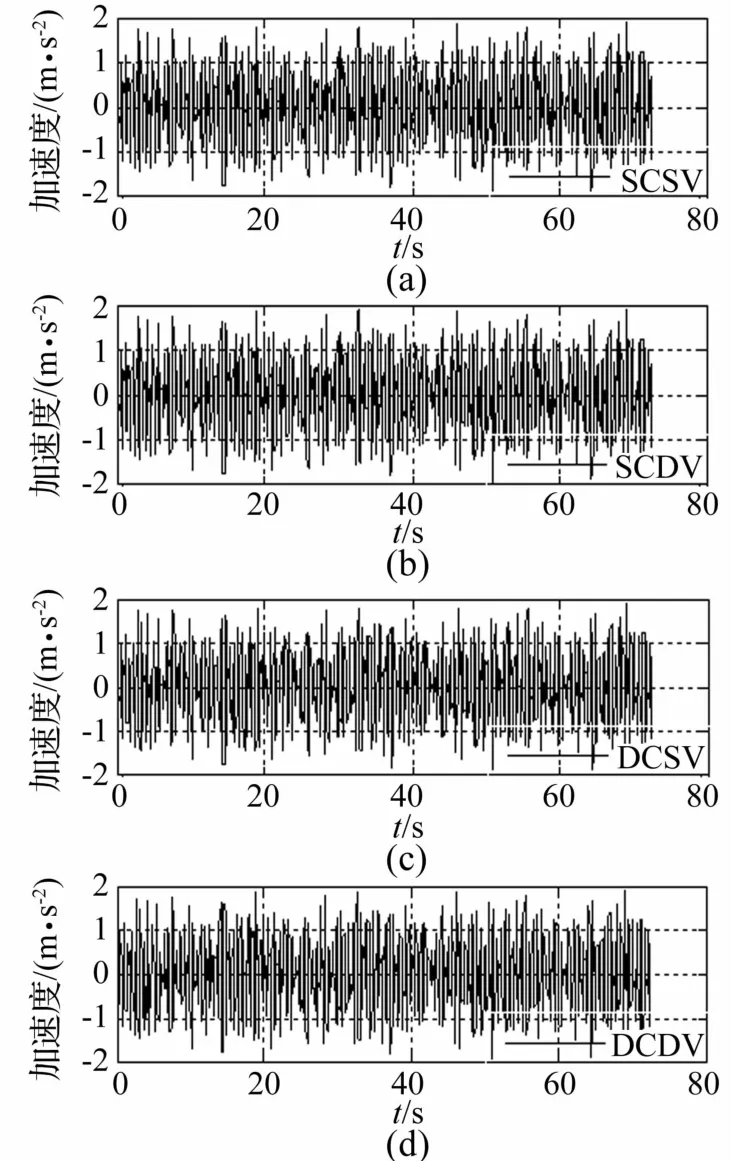
图9 行车道R2汽车队首车竖向加速度时程Fig.9 Vertical carbody acceleration time histories of the first road vehicle on R2 roadway

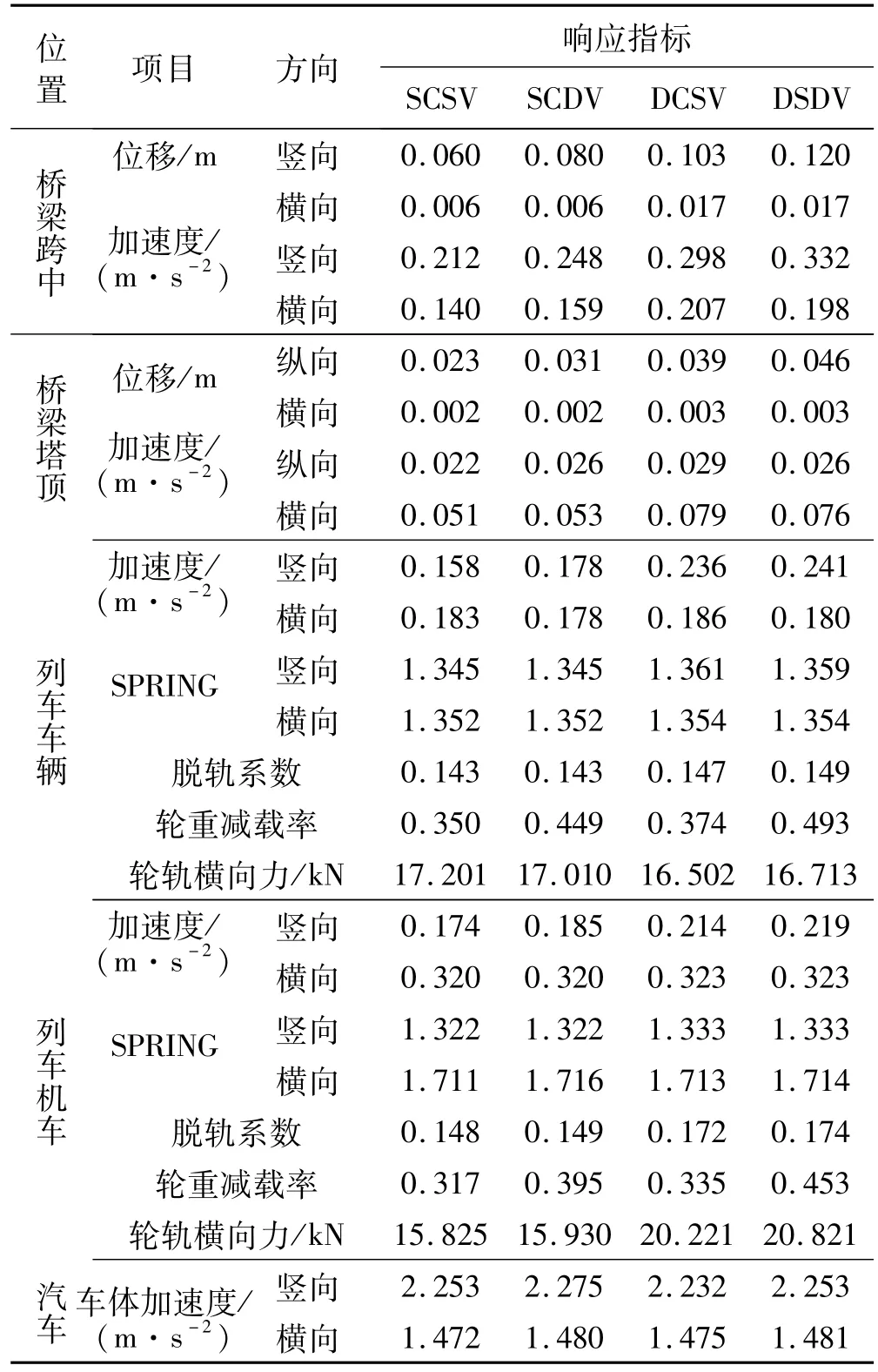
表2 桥梁与车辆响应及运行安全性、舒适性指标Tab.2 Maximum of bridge and vehicle responses and operational safety and comfort index

由于车－桥耦合振动问题的复杂性，很难从理论上直观分析哪种情况考虑汽车车辆动力作用，哪种情况下可不考虑，因此进行特大跨度公铁两用桥梁车－桥耦合振动分析时，建议建立列车－桥梁－汽车耦合振动分析模型，模拟各种可能的列车、汽车同时过桥工况，确保列车运行安全。

3 结 论

（1）视汽车为动力子系统，同时考虑列车子系统与桥梁子系统，汽车子系统与桥梁子系统间动力相互作用，建立公铁两用桥梁列车－桥梁－汽车耦合振动分析模型，为准确描述汽车车辆及铁路车辆同时通过公铁两用桥梁时车辆及桥梁子系统运动状态、准确评价该桥的行车安全性及舒适性提供新的模式。

（2）编制公铁两用桥梁列车－桥梁－汽车耦合振动仿真分析软件，利用该软件对某公铁两用大桥方案进行铁路列车与公路汽车同时过桥时车－桥耦合振动仿真计算结果表明，方案桥总体竖向、横向刚度较大，车辆运行平稳性较好，车辆运行安全。

（3）通过数值算例知，列车与汽车同时过桥时，随桥上汽车车队增多，列车机车及车辆的竖向加速度最大值、脱轨系数最大值、轮重减载率最大值明显增大，汽车对列车运行安全性影响不利。进行特大跨度公铁两用桥梁车－桥耦合振动分析时，建议建立列车－桥梁－汽车耦合振动分析模型，对各种列车与汽车同时过桥工况进行模拟，确保列车运行安全。

［1］Fryba L.Dynamics of railway bridges（2ndED）［M］.London：Telford，1996.

［2］夏禾，张楠.车辆与结构动力相互作用［M］.北京：科学出版社，2005.

［3］曾庆元，郭向荣.列车过桥时变系统振动分析理论与应用［M］.北京：中国铁道出版社，1999.

［4］Yang Y B，Yau J D.Vehiclebridge interaction for dynamic analysis［J］.Journal of Structural Engineering，ASCE，1997，123（11）：1512－1518.

［5］高芒芒.高速铁路列车－线路－桥梁耦合振动及列车走行性研究［D］.北京：铁道部科学研究院，2001.

［6］何发礼，李乔.曲率和超高对曲线梁桥车桥耦合振动的影响［J］.桥梁建设，1999，3：5－7.HE Fali，LI Qiao.Curvature and super elevation effects on coupled vibration of vehicle and curved bridge［J］.Bridge Construction，1999，3：5－7.

［7］吴定俊.提速线上桥梁振动理论与横向动力性能的研究［D］.上海：同济大学，2005.

［8］郭薇薇，夏禾，De Roeck Guido.意大利高速铁路Sesia大桥的动力特性及车桥耦合振动分析［J］.振动与冲击，2013，32（15）：82－88.GUO Weiwei， XIA He， De Roeck Guido. Dynamic characteristics and coupling vehiclebridge vibration anlysis of the high speed railway Sesia bridge in Italy［J］.Journal of Vibration and Shock，2013，32（15）：82－88.

［9］Cai C S，Chen S R.Framework of vehiclebridgewind dynamic analysis［J］.Journal of wind Engineering and Industrial Aerodynamics，2004，92：579－607.

［10］Han Wanshui，Chen Airong.Threedimensional coupling vibration of windvehiclebridge systems［J］.China Civil Engineering，2007，40（9）：53－58.

［11］陈艾荣，王大磊，庞加斌.跨海长桥风致行车安全研究［J］.桥梁建设，2006，3：1－4.CHEN Airong，WANG Dalei，PANG Jiabin.Study of windrelated riding safety on long seacrossing bridge［J］.Bridge Construction，2006，3：1－4.

［12］司学通.轻轨车辆与斜拉桥动态耦合系统的数值模拟方法及应用［D］.广州：中南大学，2007.

［13］Chen Shangyou，Liu Gao，Lu Ping.Simulation and analysis of coupled vibration of monorail trainbridgeroad vehicle system［C］.／／ZHAI Wanming.Advances in environmental vibration［A］.Beijing：Science Press，2011：494－502.

［14］李小珍，强士中.大跨度公铁两用斜拉桥车桥动力分析［J］.振动与冲击，2003，22（1）：6－9.LI Xianzhen，QIANG Shizhong.Vehiclebridge dynamic analysis for long span highway and railway bipurpose cablestayed bridge［J］.Journal of Vibration and Shock，2003，22（1）：6－9.

［15］刘海涛.强风作用下列车－汽车－桥梁时变系统的动力响应及行车安全性舒适性研究［D］.广州：中南大学，2011.

［16］王福天.车辆系统动力学［M］.北京：中国铁道出版社，1994.

［17］Zhang Nan，Xia He，Guo Weiwei，et al.A vehiclebridge linear interacted model and its validation［J］.International Journal of Structural Stability and Dynamics，2010，10（2）：335－361.