基于机床刀具加工变形研究的铣削工艺参数优化方法

迟玉伦，李郝林

（上海理工大学 机械工程学院，上海 200093）

数控铣削加工过程中在切削力作用下机床刀具变形引起的刀具与工件间相对位置变化成为影响机床加工精度的重要因素。已有对铣削刀具变形建模补偿进行的诸多研究［1－8］。张臣等［2］以球头铣刀为研究对象，建立球头铣刀刀具变形引起的加工误差仿真预测模型。Denkena等［3］提出适应主轴系统铣削加工过程中对刀具静、动态变形进行补偿并取得较好效果。Habibi等［4］通过对铣削刀具切削变形建模，经数控系统程序对刀具切削路径进行补偿，并实验证明该方法的有效性；但铣削刀具变形补偿研究中建模控制过程复杂，难以实际应用。因此，本文提出通过优化铣削工艺参数减小刀具变形量、提高加工精度方法。

本文据铣床刀具系统动刚度测量计算及铣削力模型，提出基于遗传算法的铣削工艺参数优化方法。通过阶跃响应实验获得机床刀具系统动刚度，并利用正交实验法准确获得铣削力模型；对实验机床铣削工件主轴转速、进给速度、切削宽度及切削深度等工艺参数进行数学优化；开发设计在线测量刀具变形及铣削力实验装置，并分别对优化前后工艺参数进行实验验证，结果证明该方法有效、实用。

1.1 机床刀具系统动刚度模型

1 机床铣削工艺参数优化模型

图1的机床－刀具系统可简化为X，Y方向相互垂直的二自由度振动系统［9］，即

式中：Mx，My分别为X、Y方向机床－刀具系统质量；Cx，Cy分别为 X、Y方向机床 －刀具系统阻尼；Ksx，Ksy分别为X、Y方向机床－刀具系统刚度；Fx，Fy分别为X、Y方向刀具切削力分力。

经拉普拉斯转换可得

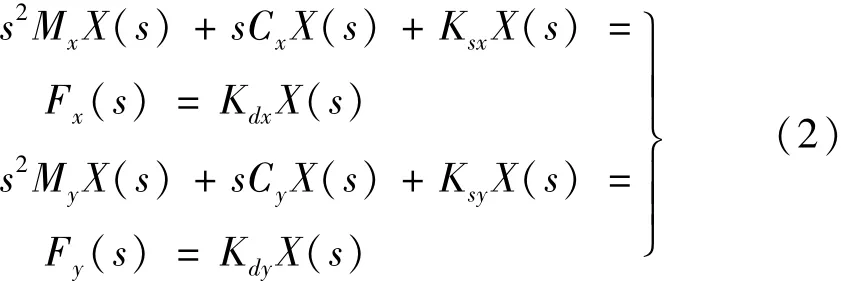
式中：Kdx，Kdy分别为 X、Y方向机床 －刀具系统动刚度［10］，可表示为

式中：Ksx，Ksy分别为X、Y方向机床 －刀具系统静刚度；ξx，ξy分别为 X、Y方向机床 －刀具系统阻尼比；λx，λy分别为 X、Y方向机床 －刀具系统交变频率 ω与固有频率 ω 之比，ω＝， j为铣刀齿数，v为主轴ns转速。

图1 铣削刀具系统动力学模型Fig.1 Milling tool system dynamic model

1.2 铣削力模型

式中：vs为刀具主轴转速；fw为工件进给速度；ae为刀具切削深度；N为刀具齿数；Ktc为刀具切向切削力系数；Krc为刀具径向切削力系数；Kte为刀具切向刃口力系数；Kre为刀具径向刃口力系数；Kac为刀具轴向切削力系数；Kae为刀具轴向刃口力系数；ex为切出角；st为切入角。

顺铣时，切入、切出角可表示为

逆铣时，切入、切出角可表示为

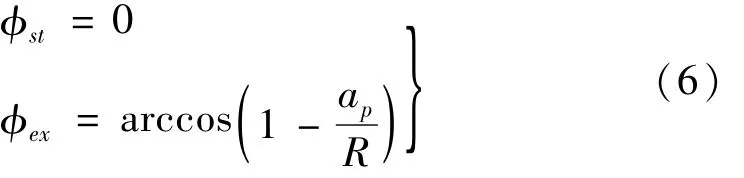
式中：ap为刀具切削宽度；R为切削铣刀半径。

1.3 铣削工艺参数优化方法

由加工工艺参数可确定铣刀X，Y方向铣削力大小。结合式（3）、（4）可求出在一定切削工艺参数下铣削刀具X，Y向的动态变形量为

结合铣削加工效率及尺寸要求，即可分析在铣削工艺参数vs，ap，fw，ae下铣削刀具最大切削变形量。本文利用遗传算法对铣削工艺参数进行优化［12］。设主轴转速为vs，切削宽度为ap，工件进给速度为fw，刀具切削深度为 ae；每齿切削量 ft＝fw／（jvs）的约束条件为vsmin≤vs≤vsmax，apmin≤ap≤apmax，fwmin≤fw≤fwmax，aemin≤ae≤aemax，ftmin≤ft≤ftmax，对应任一组参数｛vs，ap，fw，ae，｝，据式（7）可计求出铣削刀具的总变形铣削材料去除率Q＝apfwae大于Q1（Q1为设定的去除率值），建立目标优化函数 δmin，Qmax为

设世代数为n，个体数为k，变量个体位长为l，交叉率为m1，突然变异率为m2。将所得遗传算法优化后主轴转速vs，切削宽度ap，工件进给速度fw，刀具切削深度ae作为机床加工工艺参数。

2 实验研究

2.1 铣床刀具系统静刚度测量计算

本实验在沈阳机床厂VMC1165B立式加工中心，工件材料45钢，铣刀型号MG－2EA35M－D10－M。实验过程见图 2（a），压力传感器型号 KISTLER 9323AA，量程设为1 kN，灵敏度 －9.6 pc／N；电涡流位移传感器型号为MICRO－EPSILON eddyNCDT 3010，量程1 mm，分辨率小于0.05μm。通过力传感器对刀具刀尖位置施加X方向力F1，电涡流位移传感器测出刀具刀尖变形量Δx，求出刀具系统在X方向静刚度为Ksx＝＝3.46×106N／m；同样得刀具系统在Y方向静刚度为 Ksy＝3.32×106N／m。

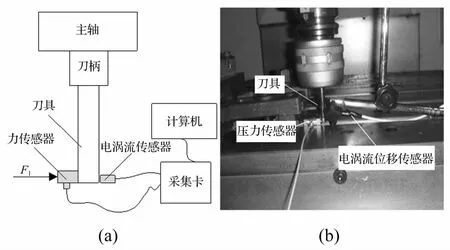
图2 铣削刀具静刚度测量Fig.2 Milling tool static stiffness measurement

2.2 铣床刀具系统固有频率及阻尼比测量计算

实验过程见图3，压力传感器型号为 KISTLER 9301B，量程设为2 kN，灵敏度－4 pc／N。在刀具X方向施加拉力F2＝100 N作为系统输入信号；用剪刀将细绳瞬间剪断，利用电涡流位移传感器获得刀具位移振动输出信号。为减小拉绳弹性影响应尽量缩短细绳长度或其它部分改用刚性较大钢丝绳（图3（b）中白色钢丝绳）。利用阶跃响应频响函数求出机床－刀具系统 X方向固有频率 ωnx＝890 Hz，阻尼比 ξx＝0.002 27；同样可得刀具系统Y方向固有频率ωny＝886 Hz，阻尼比 ξy＝0.003 42。

图3 铣削刀具动刚度测量Fig.3 Milling tool dynamic stiffness measurement

据刀具系统各方向静刚度、固有频率及阻尼比测量结果，可得刀具系统X，Y方向动刚度关系为

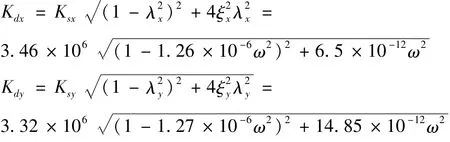
2.3 铣床力模型系数测量计算

用正交实验与偏最小二乘回归法［13］确定铣削力模型中各系数值以获得准确的铣削力模型。实验见图4。用KISTLER 9257B三向测力仪对铣削加工进行测试，选L9（34）正交试验方案安排各种测试。

选主轴转速、进给速度、铣削深度及铣削宽度等工艺参数不同数值作为该正交实验因素水平，见表1。

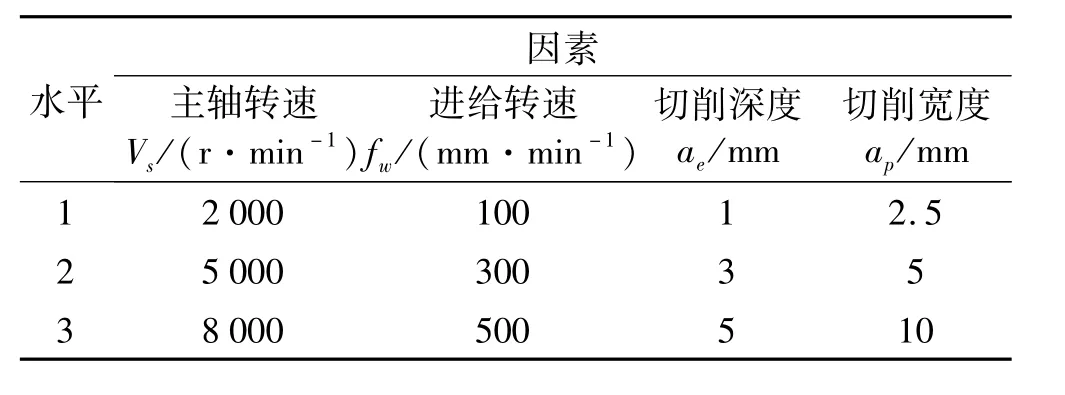
表1 正交试验因素水平表Tab.1 The orthogonal experiment parameters

在每组正交设计实验中用三向测力仪测得X，Y方向铣削力见表2。

表2 正交试验设计表Tab.2 Orthogonal experimental design

利用偏最小二乘回归法将铣削力模型与实验测量数据拟合求得铣削力模型各系数值为刀具切向切削力系数 Ktc＝1 865.1，刀具径向切削力系数 Krc＝736.2，刀具切向刃口力系数Kte＝113.5，刀具径向刃口力系数Kre＝158.7，由此获得较可靠的铣削力数学模型。

2.4 铣削工艺参数优化结果

设铣削各工艺参数约束条件为主轴转速1 000 r／min≤vs≤8 000 r／min，切削宽度 0.1 mm≤ap≤10 mm，工件进给速度 100 mm／min≤fw≤500 mm／min，刀具切削深度0.1mm≤ae≤5 mm，每齿切削量0.01 mm据式（8）目标优化函数为

选世代数30，个体数100，变量个体位长l＝9，交叉率0.6，突然变异率0.001。得铣削工艺参数优化结果为主轴转速 vs＝7 500 r／min，切削深度 ae＝3.2 mm，切削宽度 ap＝7.5 mm，工件进给速度 fw＝301 mm／min。

2.5 实验验证

为验证铣削工艺参数优化方法的有效性、实用性，本文设计的在线测量铣削刀具变形及铣削力装置可同时测量铣削刀具变形及铣削力。采用2个电涡流位移传感器与KISTLER 9257B三向测量仪在线测量铣削刀具加工过程中变形量及铣削力，实验方案见图5。

图5 在线测量铣削刀具变形及铣削力Fig.5 Milling tool deformation and force online measurement

通过专用夹具将电涡流位移传感器1、电涡流位移传感器2固定在刀具处，利用电涡流非接触式原理在线测量刀具位置变形量。电涡流传感器1测量刀具X向变形，电涡流传感器2测量刀具Y向变形。两电涡流位移传感器测量信号、铣削力信号通过数据采集卡由计算机获得，采样频率设为2 000 Hz。据两电涡流位移传感器测量结果，利用悬臂梁挠度计算式计算刀具刀尖变形量。将优化前后两组参数分别进行实验验证，结果见表3。由表3已证明工艺参数优化方法的有效性。

表3 实验验证结果Tab.3 The verification results of experiment

3 结 论

（1）针对铣削加工过程中刀具变形问题本文据机床刀具系统动态特性及铣削力模型提出基于遗传算法的铣削工艺参数优化方法。

（2）本文设计的机床刀具系统静、动刚度求解阶跃响应实验方法，据实验测量数据确定铣削力模型系数，基于实验测量结果对该机床铣削工艺参数进行优化。

（3）为验证铣削工艺参数优化方法的有效性，提出在线测量铣削刀具变形及铣削力实验方法，分别对优化前、后工艺参数在线测量刀具变形及铣削力，实验结果已验证优化方法的有效性、实用性。

（4）由于本文优化数学模型未考虑颤振因素，故该方法仅适用非颤振铣削开环系统的工艺参数优化。

［1］Prickett P W，Johns C.An overview of approaches to end milling tool monitoring［J］.International Journal of Machine Tools＆Manufacture，1999，39：105－122.

［2］张臣，周水来，安鲁陵，等.刀具变形引起的球头铣刀加工误差建模［J］.南京航空航天大学学报，2008（2）：94－99.ZHANG Chen，ZHOU Shuilai，AN Luling，et al.Modeling of bal lend milling cutter deflectioninduced machining error［J］. Journal of Nanjing University of Aeronautics＆Astronautics，2008（2）：94－99.

［3］Denkena B，G mmer O，Will C，et al.Compensation of static and dynamic tool deflections during milling processes by an adaptronic spindles system［C］.2ndInternational Conference Innovative Cutting Processes＆Smart Machining，2008.

［4］Habibi M，Arezoo B，Nojedeh M V.Tool deflection and geometrical error compensation by tool path modification［J］.International Journal of Machine Tools＆Manufacture，2011，51：439－449.

［5］Saffar R J，Razfar M R，Salimi A H，et al.Optimization of machining parameters to minimize tool deflection in the end milling operation using genetic algorithm［J］.World Applied Sciences Journal，2009，6（1）：64－69.

［6］Ding Ye， Zhu Limin，Zhang Xiaojian，et al. A fulldiscretization method for prediction of milling stability［J］.International Journal of Machine Tools＆Manufacture，2010，50：502－509.

［7］Li X P，Nee A Y C，Wong Y S，et al.Theoretical modeling and simulation of milling forces［J］.Journal of Materials Processing Technology，1999，89／90：266－272.

［8］Liu Yanming Wang Chaojun.A modified genetic algorithm based optimization of milling parameters［J］.Int J Adv Manuf Technol，1999，15：796－799.

［9］刘强，李忠群.数控铣削加工过程仿真与优化［M］.北京：航空工业出版社，2011.

［10］Jenkins H E，Kurfess T R.Dynamic stiffness implications for a multiaxis grinding system［J］.Journal of Vibration and Control，1997，3：297－313.

［11］Budak E.Analytical models for high performance milling.part I： cutting forces， structural deformations and tolerance integrity［J］.International Journal of Machine Tools＆Manufacture，2006，46：1478－1488.

［12］富宏亚，韩振宇.智能加工技术与系统［M］.哈尔滨：哈尔滨工业大学出版社，2006.

［13］尹力，刘强.基于偏最小二乘回归方法的铣削力模型系数辨识方法［J］.机械科学与技术，2005（24）：269－272.YI Li，LIU Qiang.Study on the identification of the milling force parameter model based on partial least square regression and application［J］.Mechanical Science and Technology，2005（24）：269－272.