基于EEMD子带提取相关机械振动信号单通道盲源分离

孟 宗，蔡 龙

（燕山大学 电气工程学院，河北 秦皇岛 066004）

由于现代化工业生产不断发展，机械设备故障诊断技术备受关注。独立分量分析（Independent Component Analysis，ICA）为较新的信号处理方法［1］。而基于独立分量分析的盲源分离（Blind Signal Separation，BSS）方法在机械设备故障诊断及状态监测中已获得成功应用［2］。该方法大多局限于超定或正定假设条件，即观测信号数目（传感器个数）需多于或等于源信号数目，且源信号需满足统计独立要求；但在实际机械设备故障检测中某部件的故障信息常受同一设备不同组件振动激励影响，时域上表现为信号具有一定相关性；且机械故障源数并非已知，观测信号数目不少于源信号数目假设难以满足，因此用标准的ICA方法不能准确分离源信号。

为解决传统机械故障盲源分离方法在欠定条件下（观测信号个数少于源信号个数）的失效问题，Li等［3－4］对基于系数表示的欠定盲源分离方法进行研究；Fabian等［5］提出基于中值的聚类算法，可实现欠定状况下盲分离。以上算法基础为源信号的稀疏表示。信号稀疏性较差时则不能实现好的分离效果。毋文峰等［6］将经验模态分解（Empirical Mode Decomposition，EMD）与盲源分离结合用于机械故障诊断，不仅实现单观测通道下机械振动信号盲分离，亦能克服源信号稀疏性限制。该方法因在源信号相互统计独立前提下实现，故存在模态混叠缺陷［7］。对统计相关源的盲源分离问题，张延良等［8］采用“两步法”对瞬时混合的相关源信号进行盲分离，但该算法要求在某些时刻空间仅存在一个源信号；周晓峰等［9］提出基于小波包分解的相关机械振源盲源分离方法，亦存在波包分解层数确定问题；Li等［10］将相关源信号分成若干组后进行处理，虽组内源信号可以相关，但信号间需保证相互统计独立。相关源盲分离方法多在超定或正定假设条件下进行，对欠定或单观测通道条件下相关源盲分离问题研究较少。

虽EMD自适应分解性等优点使其在机械故障诊断领域得以应用［11］，但亦存在模态混叠现象。对此Wu等［12］提出总体经验模态分解 （Ensemble Empirical Mode Decomposition，EEMD）方法。即将噪声辅助分析用于EMD以促进抗混分解，能有效抑制混叠现象。本文结合EEMD算法优点，在相关振源信号部分子带满足统计独立假设前提下提出基于EEMD子带提取的相关机械振动信号单通道盲源分离方法，对单通道观测信号进行EEMD分解及源数估计；选择若干独立性较强子带分量重组观测信号；对新观测信号进行盲分离，并用于旋转机械振动信号分离。以某故障轴承为研究对象分析分离信号频谱特征，进行故障诊断。

1 盲源分离模型

盲源分离为在混合系统结构未知情况下仅由观测信号恢复出源信号过程。设s（t）为m个未知的独立源信号；x（t）为源信号经未知信道传输后由n个传感器采集的n维观测矢量；A为未知的n×n维混合矩阵。

无噪声时n维观测矢量x（t）为 s（t）的线性组合，用矩阵表示为

盲源分离目的为在源信号统计独立的假设前提下，据独立性测度函数寻求最优分离矩阵W，分离观测信号中独立分量，获得源信号最优估计y（t），即

大多BSS算法均针对源信号相互独立情况，对由相关源混合成的观测信号不能直接应用。若将该信号分成不同类或不同子带，子带间相互独立，可在该子带内用BSS算法。观测信号数目与源信号数目相等时，式（1）可改写为

设相关源信号s（t）存在若干相互独立子带，第i子带内相互独立，则可在该子带内用标准的独立分量分析获得 si（t）估计 yi（t），即

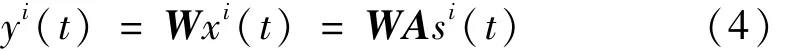
设独立子带 xi（t）由 x（t）通过线性滤波 Hi获得，则 xi（t）可表示为 si（t）的线性混合为

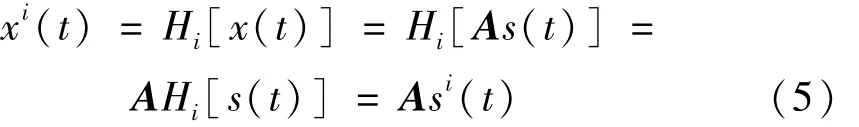
由式（4）、（5）看出，对源信号存在相关源的盲源分离问题，其混合矩阵A与分离矩阵W可通过对独立子带观测信号进行独立分量分析获得。

2 基于EEMD的子带分解

EEMD算法为改进的EMD算法，亦称噪声支持的经验模态分解，不仅能有效抑制模态混叠现象，使分解出的固有模态分量（Intrinsic Mode Function，IMF）具有确定的物理意义，且可将待分解信号与极小幅度白噪声视为整体进行EMD分解。白噪声均匀分布特性可使信号不同频率尺度投射在白噪声建立的均匀分布随机尺度上，能有效抑制IMF的不连续性。EEMD算法步骤如下：

（1）向被分解信号x（t）中加入均值0、幅值标准差为常数的高斯白噪声，进行信号归一化处理；

（2）用EMD算法分解归一化信号，获得各阶IMF分量；

（3）重复上两步骤n次，要求每次加入的随机白噪声服从正态分布；

（4）对EMD分解所得n组IMF分量集总平均。据不相关随机序列统计均值为0原理，去除人为加入高斯白噪声对真实IMF分量影响，获得x（t）的EEMD分解，即

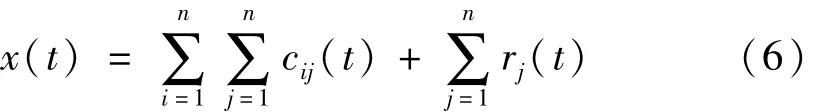
式中：cij（t）为第 j次分解所得第 i个 IMF分量；rj（t）为第j次分解所得余项。

EEMD算法可据被分析信号特征，将含相关源在内的信号分解成一系列线性、平稳的IMF分量，即将多变量信号分解成若干单分量调幅、调频信号之和。该过程可视为线性滤波。IMF分量集合可视为观测信号的子带集合。EEMD将观测信号分解p个子带分量后可表示为

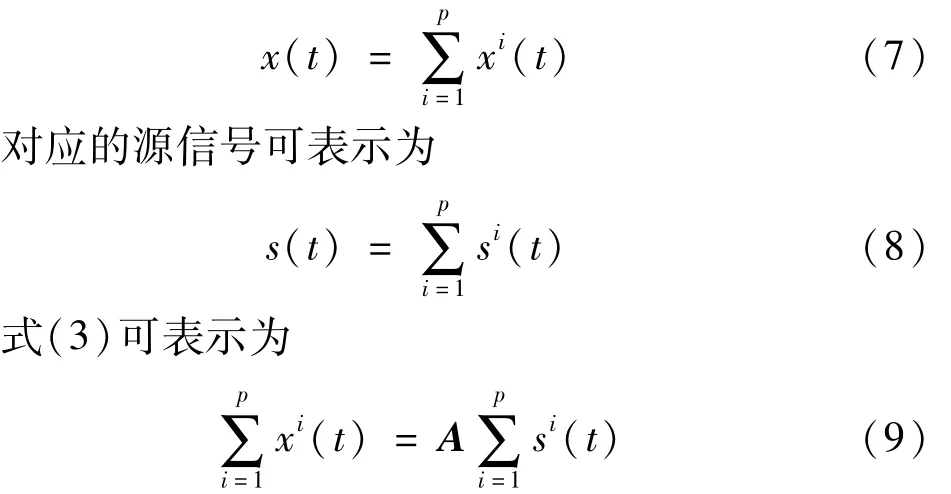
EEMD分解中加入的高斯白噪声大小直接影响其分解信号效果。加入白噪声目的为避免模态混叠，但加入白噪声太大，会影响信号中有效高频成分极值点间隔的分布特性；加入白噪声太小则无法影响信号低频极值点选取，失去尺度补充作用。因此，EEMD算法中加入白噪声准则［13］为

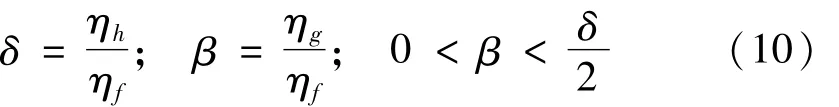
式中：ηh为分解信号有效高频成分幅值标准差；ηg为加入高斯白噪声幅值标准差；ηf为分解信号幅值标准差。一般β＝δ／4即可有效避免模态混叠。

3 基于EEMD的相关源单通道盲分离

大多盲源分离方法均需满足观测信号数目n不少于源信号数目m的假设。而对机械故障诊断中单观测通道盲源分离与源信号数目未知情况则无法直接对系统线性求逆。即使混合矩阵A已知，分离系统的解也不具备唯一性。为解决单通道下传统盲源分离算法失效问题，需估计源信号数目并对观测信号进行升维处理，以满足盲源分离假设。

EEMD分解所得子带分量可将单通道传感器观测信号拓展为含多个源信号的特征组合。若用EEMD将采集的单通道机械振动观测信号分解，选合适子带分量组成新观测信号，直至维数与源信号数目相同，即能解决观测信号数目小于源信号数目难题。

3.1 源数估计

为实现单通道机械振动信号盲分离，需估计系统中源信号数目。对单通道观测信号x（t）进行EEMD分解，获得子带分量 ci（t）（i＝1，2，…，d）及余项 rd（t）。再将x（t）与分解所得子带分量组成多维观测信号ximf（t）＝（x（t），c1（t），…，cd（t），rd（t））T。

ximf（t）相关矩阵定义为

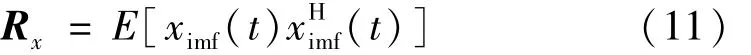
式中：“H”为复数共轭变换。

噪声为空间白色信号时，式（11）的Rx可改写为

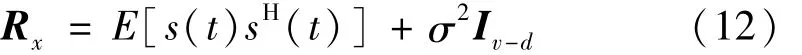
式中：v为信号 ximf（t）＝（x（t），c1（t），…，cd（t），rd（t））T的维数；Iv－d为单位矩阵；σ2为噪声功率。

对Rx进行奇异值分解，得

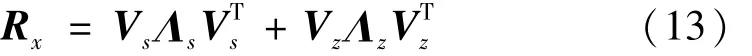
式中：Λs＝diag｛λ1，…，λd｝为 d个按递减顺序排列的主特征值；Λz＝diag｛λd＋1，…，λv｝为 v－d个噪声特征值，且 Λz＝σ2I。

理论上Rx的v－d个最小特征值等于噪声功率σ2。因此在精确估计协方差矩阵并设噪声方差相对小的前提下，可通过判断Rx最小特征值个数确定其噪声子空间维数，进而达到估计源信号个数目的；但在实际操作中Rx最小特征值不可能完全相等，且主特征值与噪声特征值间设定阈值较困难，无法准确判断噪声子空间维数。为解决阈值设定问题，采用Bayesian信息准则（BIC）估计信号与噪声子空间维数。BIC信息准则可对非高斯源信号进行源数估计，适用于机械振动信号。BIC信息准则为在Minaka Bayesian选择模型（MIBS）基础上建立的源数估计方法。MIBS可用BIC信息准则近似为

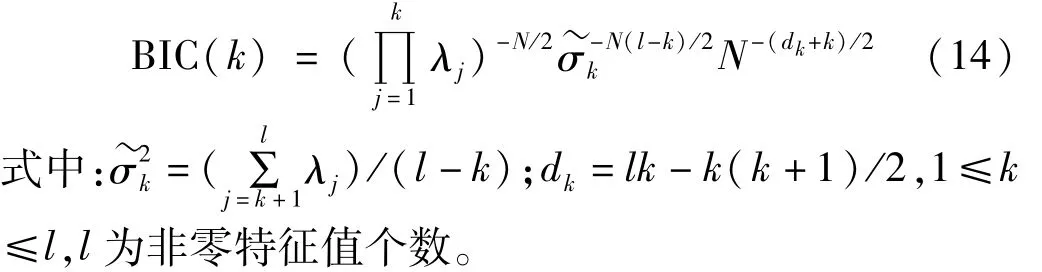
MIBS目标为寻找能使代价函数最大的序号k＝m，m即为估计的源信号个数。

3.2 互信息准则与独立子带选取

为克服模态混叠，本文用EEMD对观测信号x（t）进行子带分解。为选择合适子带分量重构成新观测信号，需选取EEMD分解所得子带。考虑EEMD分解x（t）所得子带能体现源信号信息，据式（4）、（5）知，若单一子带分量统计独立性越高该子带越能清晰体现源信号独立子带成分，越适合组成子带观测信号进行盲分离。因互信息作为衡量一组随机变量间独立性重要尺度，故将其作为子带选取准则。互信息值为非负，当一组随机变量相互统计独立时互信息趋于零。互信息值可通过互累积量近似获得［14］，即

已知源信号个数m时，据互信息标准，观测信号重构步骤为：

（1）用EEMD将单通道观测信号x（t）进行子带分解，得子带分量集合 CJ（J＝1，2，…，u）；

（2）按式（15）分别计算CJ中每个分量的归一化互信息；

（3）选取CJ中归一化互信息最小的m个子带分量组成新观测信号 xR（t），即

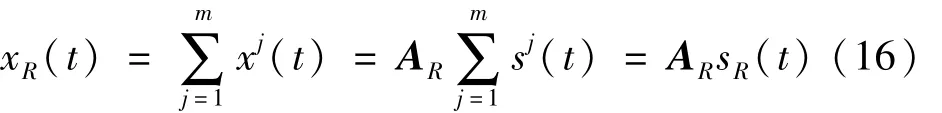
式中：sR（t）为与 xR（t）对应的重构独立源信号；AR为正定情况下新m×m混合矩阵。

3.3 预白化

白化过程能使盲源分离问题大幅简化，其本质为去相关及压缩。白化后信号只需通过正交变换即能恢复源信号。白化过程描述：定义 RxR＝E［xR（t）xHR（t）］为重构的观测信号自相关函数，与xR（t）对应源信号为sR（t），AR为m×m混合矩阵。由于RxR为对称正定矩阵，故存在特征值分解为

式中：Λx＝diag（λ1，λ2，…，λm）为 RxR特征值由大到小排列组成的对角矩阵；Vx＝［d1，d2，…，dm］为与 Λx对应的特征向量组成的正交矩阵。则白化矩阵为w0＝Λ。设 z（t）为白化后观测信号，标准白化过程可表示为

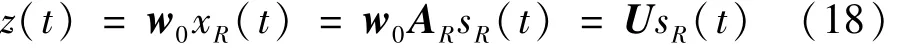
白化最终目的为使变换后随机变量z（t）自相关函数为单位矩阵 Rz＝E［z（t）zH（t）］＝I，故 U为酉矩阵。由此，通过白化处理求混合矩阵A过程转化成寻找酉矩阵U过程。

3.4 联合对角化白化后观测信号

本文盲源分离过程用特征矩阵近似联合对角化（Joint Approximate Diagonalization of Eigenmatrices，JADE）方法［15］。设 M为任意 N阶矩阵，z（t）的四阶累积矩阵Qz（M）定义为

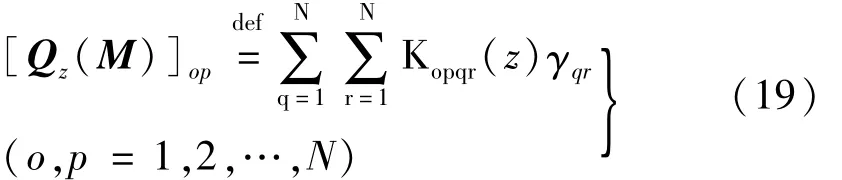
式中：Kopqr（z）为 z（t）中第 o，p，q，r分量的四阶累积量；γqr为 M第 q，r个元素。

式（18）可改为

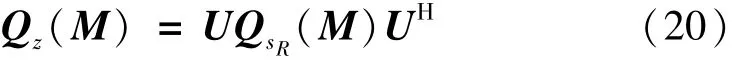
由于sR（t）中各分量相互统计独立，故其四阶累积量QsR（M）为对角阵。即矩阵U的确定可通过Qz（M）联合对角化实现；但实际操作中若只取一个M矩阵，较难获得理想结果。通常取一组矩阵M＝［M1，M2，…，MK］，并对 M中每个分量求取 Qz（MI），（I＝1，2，…，K），将问题转化为K个N×N四阶累积量矩阵近似对角化，并用UHQz（MI）U中对角元素的平方和作为对角化过程参照函数，即

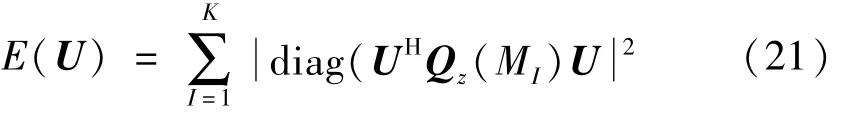
通过优化算法最小化E（U）获得酉矩阵U，即可获得源信号估计，即

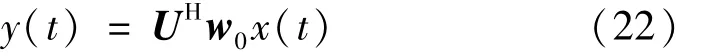
4 仿真实验

为验证本文方法分离信号的有效性及可行性，构造3个振源信号为

式中：f0＝80 Hz；s1（t），s2（t），s3（t）组成源信号s（t）。

设采样频率1 024 Hz，采样点数512，源信号时域波形见图1。为获得虚拟观测信号，任选3×3随机矩阵作为混合矩阵，即

据式（1）盲源分离模型获得3路观测信号x（t）。设监测条件受限，仅采集到1路观测信号x1（t），其时域波形见图2。由于观测信号只有1个，源信号有3个，且 s1（t），s2（t）为相关源信号，属单观测通道条件下相关源信号盲源分离问题，用本文算法进行处理。

图1 相关源信号时域波形Fig.1 Timewave of the correlated source signals

图2 单通道观测信号时域波形Fig.2 Timewave of the singlechannel observed signal

4.1 源数估计

对单通道观测信号x1（t）进行EEMD分解，获得子带分量 c1（t），…，c8（t）及残余分量 r8（t）。将 x1（t）、子带分量及残余分量组成新的多维信号 ximf（t）＝（x1（t），c1（t），…，c8（t），r8（t）），计算其相关矩阵 Rx＝E［ximf（t）xH

imf（t）］；再对 Rx进行奇异值分解，获得特征值由大到小排列的矢量 Λ＝diag｛λ1，…，λ10｝，见表1。基于相关矩阵特征值估计源信号数目为3，进一步由Bayesian信息准则计算获得源信号个数为3。

表1 相关矩阵特征值Tab.1 The eigenvalues of correlation matrix

图3 EMD分解所得子带观测信号Fig.3 The subband observed signals decomposed by EMD

图4 分离信号时域波形［16］Fig.4 Timewave of the separated signals［16］

图5 EEMD分解所得子带观测信号Fig.5 The subband observed signals decomposed by EEMD

4.2 基于EEMD的相关源盲分离

为凸显EEMD有效克服模态混叠优势，本文用EMD、EEMD算法同时对单通道观测信号x1（t）进行分离。EMD算法分解所得子带观测信号见图3。限于篇幅，据上节估计的源信号数目只选互信息最小的前3个子带分量。由图3看出，c1对应调幅信号s1（t），c2对应调幅信号 s2（t），c3对应正弦信号 s3（t）。由于相关信号源的引入c2与c3出现模态混叠。用欠定盲源分离方法（简称 EMDBSS）［16］估计源信号，结果见图 4。由图4看出，EMDBSS的分离信号能实现源信号辨识，但分离精度欠佳。此因子带分量偏离观测信号固有模式，直接影响后续盲源分离过程。由于盲源分离存在不确定性，导致分离信号与源信号存在排列顺序、幅值差异，但不影响分离结果识别。

用本文方法进行分离，EEMD分解子带见图5（此处仅给出互信息最小的前3个子带），c2对应调幅信号s1（t），c3对应调幅信号 s2（t），c5对应正弦信号 s3（t）。对比图3、图5看出，EEMD算法的子带分量能更好展现仿真信号频率组成成分、相位及周期变化等信息，并能有效抑制模态混叠。将EEMD分解所得c2，c3，c5分量重构新观测信号，白化后进行联合对角化，获得源信号估计y（t），其时域波形见图6。对比图4、图6看出，本文算法的分离效果优于EMDBSS。

图6 分离信号时域波形（本文算法）Fig.6 Timewave of the separated signals（by proposed method）

为定量评价分离效果，用源信号与分离信号相似系数作为分离的性能指标。相似系数定义：设si为源信号s的第i个分量，yj为经盲源分离的与si对应的分离量，则si与yj的相似系数为

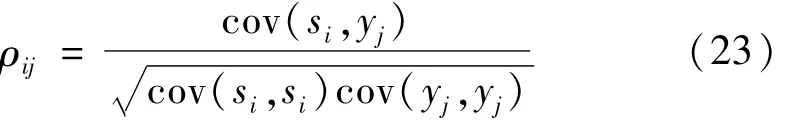
式中：cov为协方差；0≤ ρij≤1，ρij越接近于1说明盲分离算法分离的信号及与之对应的源信号越相似。

相似系数可抵消因盲分离不确定性造成的幅值尺度差异、避免源信号与分离信号幅值尺度不相同影响。两算法分离信号与源信号相似系数对比见表2。为方便对比，表中已变换分离信号排列顺序。由表2看出，本文算法分离信号与源信号相似系数更接近1，说明本文算法分离精度优于EMD－BSS算法，对频带交叠信号能实现较有效分离。此因EEMD算法将信号在固有模态子空间进行分解，将频带交叠信号分解在其它子带中。EEMD的优秀特性使算法具有更强的抗干扰性、鲁棒性。

表2 两种算法相似系数Tab.2 The similarity coefficients of the two methods

综合仿真结果，与EMD相比EEMD分解所得子带分量能避免模态混叠，物理意义更明显，且EEMD算法不存在小波分解方法的基函数选择，与盲源分离结合能克服传统独立分量分析只限于源信号相互独立、平稳、观测信号数目不少于源信号数目的局限性。可保证分离结果能充分保留源信号的非平稳特征。

5 实验研究

作为旋转机械重要组成部分的轴承运转时，因内、外圈及滚动体等各部件间相互关联，其振源间存在较强相关性。受限实验条件仅监测1路观测信号。用本文方法对内、外圈及滚动体耦合故障进行检测。实验数据源自某旋转机械故障模拟实验台，被测试轴承型号为6205－2RS SKF，为支撑电机转动轴的深沟球轴承。测试用轴承规格参数见表3。

表3 轴承规格参数Tab.3 The specification of bearing

电动机转速1 772 r／min，得转轴基频 fr＝29.5 Hz。用电火花技术加工轴承的单点故障，据轴承结构尺寸及转速，计算得轴承内圈故障特征频率fi＝159.9 Hz，外圈故障特征频率f0＝105.9 Hz，滚动体故障特征频率f0＝141.1 Hz，采样长度 2 048，采样频率 fs＝12 000 Hz。轴承运转时，通过振动传感器测得含内、外圈及滚动体故障信息的单通道观测信号见图7。

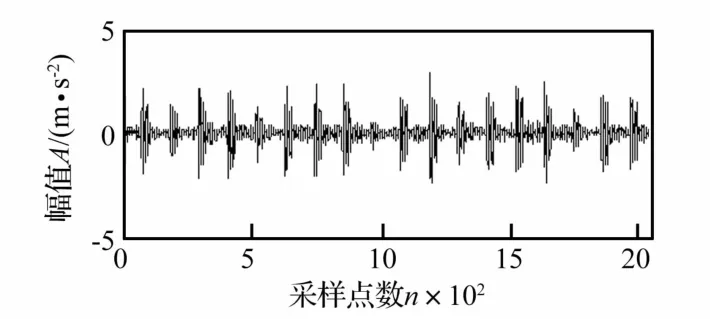
图7 单通道观测信号时域波形Fig.7 Timewave of the singlechannel observed signal

用本文方法对观测信号进行处理，获得估计源信号时域波形见图8，但由图8不能确定内、外圈故障信息。对估计源信号进行频域分析，包络谱见图9。由图9（a）看出，除58.6 Hz峰值处对应基频的二倍频外，在160.2 Hz处出现峰值。与轴承内圈故障理论频率值159.9 Hz较接近。由于实际测量环境及客观因素影响，计算值与真实值会有微小差异，但完全可断定160.2 Hz对应内圈故障特征频率。由图9（b）看出，在105.5 Hz处出现峰值，与外圈故障特征频率105.9 Hz吻合。在210.9 Hz、58.6 Hz处出现的峰值分别对应外圈故障特征频率的二倍频与基频的二倍频。由图9（c）看出，141.3 Hz处峰值与滚动体故障特征频率对应。为比较，用EMD－BSS算法对该单通道混叠信号进行分离，获得分离信号频谱见图10。对比图9、图10可知，本文方法能更好展现相关源信号的频率分布特性。由此可见，实测的轴承故障数据较理想，该方法的有效性、实用性得到验证。

图8 分离信号时域波形Fig.8 Timewave of the separated signals

图9 分离信号频谱图（本文算法）Fig.9 The frequencydomain chart of the separated signals（by proposed method）

图10 分离信号频谱图（EMDBSS算法）Fig.10 The frequencydomain chart of the separated signals（by EMDBSS）

6 结 论

（1）本文针对传统盲源分离方法难以解决实际机械故障诊断中存在的相关源、单观测通道等问题，在分析EEMD算法原理基础上，集合EEMD与盲源分离各自优势，提出基于EEMD子带提取的相关机械振源单通道盲分离方法。

（2）为满足传统盲源分离方法观测信号数目不少于源信号数目的假设将单通道观测信号进行EEMD分解，据最小互信息准则，选择相关性较小子带分量组成的新观测信号具有线性、平稳特性，符合传统独立分量分析的前提条件。

（3）通过用本文方法对仿真信号与实测轴承故障信号的分离，验证该方法可行性及优越性，亦为机械故障诊断技术提供新方法。

［1］李斌，郭瑜，刘亭伟，等.基于独立分量分析与包络阶比分析的齿轮箱多振源特征提取［J］.振动与冲击，2012，31（19）：68－72.LI Bin，GUO Yu，LIU Tingwei，et al.Multiple vibration sources characteristics extraction of a gearbox based on independent component analysis and envelope order analysis［J］.Journal of Vibration and Shock，2012，31（19）：68－72.

［2］潘楠，伍星，迟毅林，等.基于频域盲解卷积的机械设备状态监测与故障诊断［J］.振动与冲击，2012，31（12）：34－41.PAN Nan，WU Xing，CHI Yilin，et al.Mechanical equipment condition monitoring and fault diagnosis based on frequencydomain blind deconvolution［J］.Journal of Vibration and Shock，2012，31（12）：34－41.

［3］Li Y Q，Amari SI，Andrzej C，et al.Probability estimation for recoverability analysis of blind source separation based on sparse representation［J］.IEEE Transactions on Information Theory，2006，52（7）：3139－3152.

［4］Li Y Q，Amari S I，Andrzej C，et al.Underdetermined blind source separation based on sparse representation［J］.IEEE Transactions on Signal Processing，2006，54（2）：423－437.

［5］Fabian J T，Carlos G P，Elmar W L.Medianbased clustering for underdetermined blind signal processing［J］.IEEE Signal Processing Letters，2006，13（2）：96－99.

［6］毋文峰，陈小虎，苏勋家.基于经验模式分解的单通道机械信号盲分离［J］.机械工程学报，2011，47（4）：12－16.WU Wenfeng，CHEN Xiaohu，SU Xunjia.Blind source separation of singlechannel mechanical signal based on empirical mode decomposition［J］.Journal of Mechanical Engineering，2011，47（4）：12－16.

［7］程军圣，张亢，杨宇，等.局部均值分解与经验模式分解的对比研究［J］.振动与冲击，2009，28（5）：13－16.CHENG Junsheng，ZHANG Kang，YANG Yu，et al.Comparison between the methods of local mean decomposition and empirical mode decomposition［J］.Journal of Vibration and Shock，2009，28（5）：13－16.

［8］张延良，楼顺天，张伟涛.用于统计相关源信号的盲分离方法［J］.西安电子科技大学学报（自然科学版），2009，36（3）：401－405.ZHANG Yanliang，LOU Shuntian，ZHANG Weitao.Blind source separation method applicable to dependent sources［J］.Journal of Xidian University（Natural Science Edition），2009，36（3）：401－405.

［9］周晓峰，杨世锡，甘春标.相关机械振源的盲源分离方法［J］.振动与冲击，2012，31（14）：60－63.ZHOU Xiaofeng，YANGShixi，GAN Chunbiao.Blind source separation of statistically correlated sources［J］.Journal of Vibration and Shock，2012，31（14）：60－63.

［10］ Li R.Dependent component analysis：concepts and main algorithms［J］.Journal of Computers，2010，5（4）：589－597.

［11］程军圣，于德介，杨宇.EMD方法在转子局部碰摩故障诊断中的应用［J］.振动、测试与诊断，2006，26（1）：24－27.CHENG Junsheng，YU Dejie，YANG Yu.Application of EMD to local rubimpact fault diagnosis in rotor systems［J］.Journal of Vibration，Measurement＆Diagnosis，2006，26（1）：24－27.

［12］Wu Z H，Huang N E.Ensemble empirical mode decomposition：a noiseassisted data analysis method［J］.Advances in Adaptive Data Analysis，2009，1（1）：1－41.

［13］陈略，訾艳阳，何正嘉，等.总体平均经验模式分解与1.5维谱方法的研究［J］.西安交通大学学报，2009，43（5）：94－98.CHEN Lue，ZI Yanyang，HE Zhengjia，et al.Research and application of ensemble empirical mode decomposition principle and 1.5 dimension spectrum method［J］.Journal of Xi’an Jiaotong University，2009，43（5）：94－98.

［14］Cardoso J F.Dependence，correlation and gaussianity in independent component analysis［J］.Journal of Machine Learning Research，2003（4）：1177－1203.

［15］Cardoso J F，Souloumiac A.Blind beamforming for nonGaussian signals［J］.Radar and Signal Processing，IEE Proceedings F，1993，140（6）：362－370.

［16］李志农，吕亚平，范涛，等.基于经验模态分解的机械故障欠定盲源分离方法［J］.航空动力学报，2009，24（8）：1886－1892.LI Zhinong，LYaping，FAN Tao，et al.Underdetermined blind source separation method of machine faults based on empirical mode decomposition［J］.Journal of Aerospace Power，2009，24（8）：1886－1892.