自然光反射折射偏振态的光矢量分析
苏景顺 马丽红
(河北建筑工程学院数理系,河北 张家口 075000)
0 引 言
在光学教程中[1],自然光入射到两种媒质分界面发生反射、折射时的偏振规律是人们所熟知的:反射光为垂直极化波占优势的部分偏振光,折射光为平行极化波占优势的部分偏振光.仅当入射角i等于布儒斯特角iB时,反射光是由垂直极化波构成的完全偏振光,折射光是平行极化波占优势的部分偏振光.布儒斯特角iB由下式确定.
自然光反射、折射时的偏振状态通常用作图法表示.作图法简单、直观,但只能定性地表示反射光、折射光的偏振化程度.需要明确的是,作图法绘出的是光矢量,而非光强.用作图法定性地表示反射光、折射光的偏振化程度,重要的在于表示垂直极化波与平行极化波的相对关系.下面根据菲涅耳公式,定量分析自然光射向非铁磁性媒质界面时反射光、折射光的偏振状态,特别是垂直极化波与平行极化波的相对关系,并指出作图法表示偏振光应注意的几个问题.
1 以入射角、折射率表示的菲涅耳公式

(1)
(2)
(3)
(4)
(5)
(6)

(7)
结合折射定律
(8)
可以将式(1)、式(2)、式(4)、式(5)表示的反射系数和透射系数改用入射角i与媒质的折射率n表示.垂直极化波的反射系数Γc、透射系数Tc分别为
(9)
(10)
垂直极化波的反射系数Γc与透射系数Tc满足关系
1+Γc=Tc
平行极化波的反射系数Γp、透射系数Tp分别为
(11)
(12)
平行极化波的反射系数Γp与透射系数Tp满足关系
1+Γp=nTp
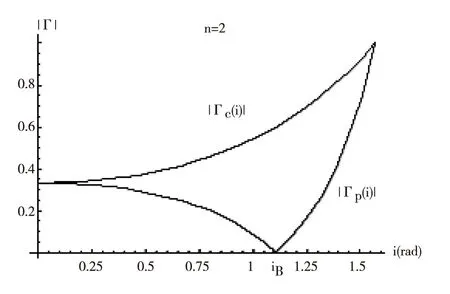
图1
式(9)~式(12)即是垂直极化波和平行极化波从空气入射到非铁磁性材料界面时的菲涅耳公式.显然,在入射波从空气射向非铁磁性材料界面的条件下,无论是垂直极化波,还是平行极化波,反射系数Γ、透射系数T均为实数,且由入射角i和媒质的折射率n决定.
自然光可以看作是垂直极化波与平行极化波两种成分相等的光波.下面用式(9)~式(12)表示的菲涅耳公式分析自然光从空气射向非铁磁性介质表面发生反射、折射时的偏振规律.
2 反射光中两种极化波与入射角的关系
当自然光从空气射向非铁磁性材料界面发生反射时,根据式(9)、式(11)可以绘出反射光中垂直极化波反射系数Γc、平行极化波反射系数Γp的绝对值随入射角i变化的规律,如图1所示(菲涅耳公式中的反射系数取负值表示方向,分析量值关系取绝对值.为突出主要特征,设媒质的折射率n=2).
分析式(9)、式(11)和图1可得出以下结论:
(1)平行极化波的反射系数以布儒斯特角iB为转折点,先减小,再较快地增大.而垂直极化波的反射系数则随入射角i单调增大.
(2)当入射角等于布儒斯特角iB时,平行极化波的反射系数为零,平行极化波完全不能反射.这时反射光由垂直极化波构成,即反射光为垂直入射面振动的平面偏振光.
(3)需要指出的是:自然光以布儒斯特角iB入射,反射光是完全偏振光,但其光强与媒质的折射率有关.例如,垂直极化波从空气射向折射率n=1.5253的冕玻璃时,iB=56.3°,反射系数约为0.384,光强约反射15%;当垂直极化波从空气射向折射率为n=2.0的红锆石时,iB=63.5°,反射系数约为0.6009,光强约反射36%;随着媒质折射率的增大,反射光强也增加.而多数教科书[3]忽略了折射率对反射光强的影响,认为“以起偏角入射,反射光虽然是完全偏振光,但光强较弱”,这是欠准确的.
用作图法表示反射光的偏振态,重要的在于表示平行极化波与垂直极化波的相对关系.为了了解这种相对关系,根据式(9)、式(11)可以得到反射光中平行极化波反射系数Γp与垂直极化波反射系数Γc绝对值的比值为
(13)
根据式(13)可绘出图2(设自然光从空气射向n=1.5253的冕玻璃).

图2
分析式(13)和图2可得出以下结论:
(1)反射光中平行极化波的反射系数Γp与垂直极化波的反射系数Γc绝对值的比值以布儒斯特角iB=0.990488(约56.75°)为转折点,形成V型反转.这说明当入射角接近布儒斯特角时,反射光的偏振化程度提高;远离布儒斯特角时,反射光的偏振化程度降低.
(2)由于
这说明自然光接近垂直入射或接近水平掠射时,反射光中平行极化波与垂直极化波两种成分相等,反射光基本上仍然是自然光.
表1列出了自然光从空气射向冕玻璃(n=1.5253)时,反射光中平行极化波与垂直极化波的比值为某些特殊值所对应的入射角,可供参考.

表1
3 折射光中两种极化波与入射角的关系
根据式(10)、式(12)可绘出自然光从空气射向非铁磁性介质折射时,垂直极化波透射系数Tc、平行极化波透射系数Tp的绝对值随入射角i的变化规律,如图3所示(菲涅耳公式中的反射系数取负值表示方向,分析量值关系取绝对值.为突出主要特征,设媒质的折射率n=2).

图3
分析式(10)、式(12)和图3可得出以下结论:
(1)折射光中无论是垂直极化波的透射系数,还是平行极化波的透射系数,都将随入射角i的增大而减小.然而平行极化波的透射系数始终不小于垂直极化波的透射系数.这说明折射光始终是平行极化波占优势.
(2)当入射角较小时,两种极化波的透射系数较大,折射光强较强;当入射角较大,特别是接近90°水平掠射时,两种极化波的透射系数接近为零,折射光强很弱.
为了了解折射光中平行极化波与垂直极化波的相对关系,根据式(10)、式(12)可以得到平行极化波透射系数Tp与垂直极化波透射系数Tc绝对值的比值为
(14)
根据式(14)可绘出图4(设自然光从空气射向n=1.5253的冕玻璃).
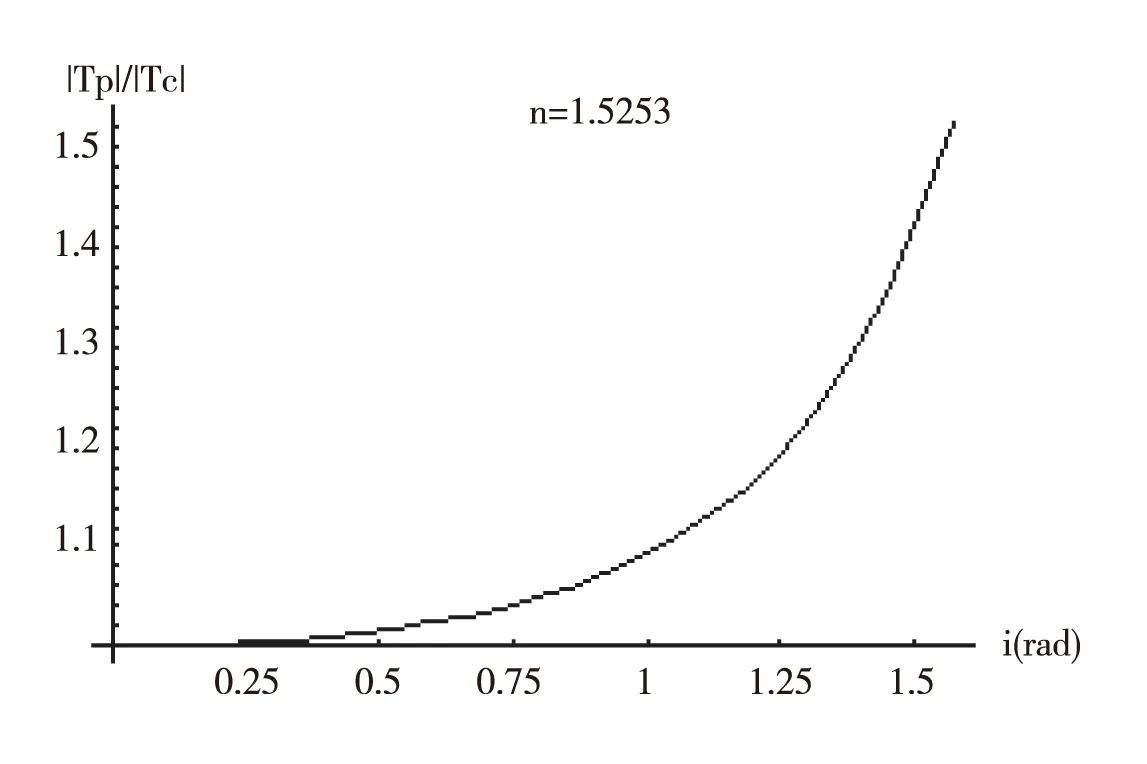
图4
分析式(14)和图4,可得出以下结论:
(1)折射光中平行极化波的透射系数与垂直极化波的透射系数的比值随着入射角i的增加而单调地增加,这一结论与文献[4]的研究结果是一致的.当入射角i较小时(i<0.397335 rad,约22.76°),平行极化波的透射系数与垂直极化波的透射系数基本相等(相差<1%),这时折射光的偏振化程度较低;当入射角i较大时,平行极化波的透射系数明显地大于垂直极化波的透射系数,折射光的偏振化程度提高.
(2)自然光以布儒斯特角iB入射,反射光的偏振化程度最高,但折射光的偏振化程度并不一定很高,而是与媒质的折射率有关.例如,自然光从空气射向折射率n=1.5253的冕玻璃时,
iB=arctann=arctan1.5253=0.990488(rad)
(15)
这时的折射光是平行极化波略占优势的部分偏振光,偏振化程度很低;当自然光从空气射向折射率为n=2.0的红锆石时,
iB=arctann=arctan2.0=1.10828(rad)
这时折射光的偏振化程度则有所提高.这说明自然光以布儒斯特角iB入射,折射光的偏振化程度随着媒质折射率的增大而提高.因此,一些教科书[5]认为“自然光以起偏角入射,反射光的偏振程度最高,折射光的偏振程度也最高”是不妥的.或在一些教科书[6]中忽略了折射率的影响,简单地认为“自然光以起偏角入射,折射光的偏振化程度却不高”的表述也是欠准确的.
(3)由于
这表明折射光的偏振化程度虽然随入射角i的增加而提高,但平行极化波的透射系数与垂直极化波的透射系数的比值不大于媒质的折射率n. 例如,自然光从空气射向折射率n=1.5253的冕玻璃,平行极化波与垂直极化波的比值不大于1.5253.而在一些教科书[7]中表示折射光偏振化程度的图示往往夸大了平行极化波的成分.
表2列出了自然光从空气射向n=1.5253的冕玻璃时,折射光中平行极化波与垂直极化波的比值为若干特殊值及其对应的入射角,可供参考.

表 2
综上所述,自然光反射、折射时的偏振态取决于平行极化波与垂直极化波的相对关系.了解这种相对关系随入射角、折射率的变化规律,不仅可以对反射、折射时的偏振态有较清晰的认识,而且在用作图法表示偏振光时所绘图示更为合理.
参 考 文 献
[1]姚啓钧.光学教程[M].北京:人民教育出版社,1981.281
[2]谢处方,饶克谨.电磁场与电磁波[M].北京:电子工业出版社,1999.177
[3]张三慧.大学物理学(3)[M].北京:清华大学出版社,2000.223
[4]王静,宋连科,等.自然光在多层介质分界面上折射时的偏振度[J].大学物理,2006.4:36~38
[5]严导淦.物理学(下册)[M].北京:北京邮电大学出版社,2008.6.196
[6]赵近芳.大学物理学(下)[M].北京:清华大学出版社,2000.223
[7]程守洙,江之永.普通物理学(3)[M].北京:高等教育出版社,1998.251

