强迫激励下CFRP斜拉索面内分叉特性*
康厚军,赵跃宇,朱志辉,解维东
(1.湖南大学 土木工程学院,湖南 长沙 410082; 2.中南大学 土木工程学院,湖南 长沙 410075)
CFRP(Carbon Fiber Reinforced Polymer)斜拉桥是近几年来出现的一种具有相当发展前景的新型大跨度桥梁,国内外已建成CFRP斜拉索斜拉桥6座.CFRP是一种增强型的碳纤维复合材料,被广泛应用于航空航天和机械工程等领域.CFRP斜拉索能克服传统钢质拉索的锈蚀、疲劳、极限长度小和承载效率低等问题,它轻质(容重约为钢材的1/5)、高强(弹性模量最高可达1 000 GPa,抗拉强度可达2 700 MPa[1])和耐腐蚀等特点,使得它作为斜拉索具有相当大的竞争力,并且随着斜拉桥跨度的增大,这种优势将越来越明显.
目前,国内外对于CFRP斜拉索动力学特性的研究还比较少,主要基于各向同性假设的传统拉索理论,利用有限元方法对其动力学问题开展研究.张新军等[2]基于斜拉桥和悬索桥的有限元模型,研究了相同刚度的CFRP索和钢索在两种桥型中的空气动力稳定问题,发现CFRP索在悬索桥中由于其较大的扭转频率而具有更好的空气动力稳定性.张鹤和谢旭[3-4]基于各向同性假设,采用有限元方法研究了车辆荷载作用下大跨度斜拉桥中CFRP拉索的非线性振动行为,发现在车辆荷载下,CFRP斜拉索的振动比刚索大;在横向风荷载作用下,CFRP拉索的横向变形基本上与钢索相同.后来,谢旭等[5]应用柔性拉索的非线性振动理论,研究了横向脉动风荷载作用及支点激励下的CFRP拉索非线性振动,研究结果表明,脉动风虽然导致拉索出现不规则的竖向和横向水平振动,但不会改变拉索的参数振动特性.另外,Xiong等[6]和Fang等[7]利用有限元方法和实验对CFRP斜拉桥的特征频率和模态等基本动力学性能进行了研究.
对于CFRP拉索的非线性振动问题,目前国内外的研究也主要基于传统拉索的各向同性动力学理论.梅葵花等[8]建立了CFRP拉索的非线性参数振动模型,对相同条件下的CFRP拉索和钢拉索,采用数值方法分析了频率匹配比、拉索静拉力、激励幅值以及阻尼等因素对拉索参数振动特性的影响.吴晓等[9]对比研究碳纤维缆索悬索桥与钢缆索悬索桥的竖向非线性自由振动,利用Galerkin方法及L-P法求出了悬索桥竖向非线性自振的近似解,研究表明温度升高使悬索桥非线性自振频率降低.Kang等[10]研究了在参数激励下CFRP拉索和钢质拉索的主共振和亚谐波共振,发现CFRP拉索弹性模量取值不同,对拉索的非线性振动性能有较大的影响,可以改变拉索的软硬弹簧特性,这有利于拉索的减振设计.
近几年来,对CFRP斜拉索动力学特性的研究,开始考虑其材料各向异性的问题.李志江[11]采用各向异性的材料本构关系,考虑了弯曲刚度、剪切刚度和扭转等因素影响,推导出了对 CFRP 材料斜拉索分析具有针对性而且计算精度较高的梁模型方程,研究了在外部激励荷载作用下CFRP斜拉索主参数共振时的非线性动力学特性.该方面的研究工作才刚刚起步,还有待进一步揭示CFRP拉索的非线性动力学特性和机理,以期为大跨度索支撑桥梁的设计和建造提供理论支撑和有建设性的建议.
本文基于CFRP斜拉索的各向异性材料特性和斜拉索的基本力学性能,将其假定为横向各向同性材料,建立了其非线性动力学控制偏微分方程.将风对拉索的涡激等作用简化为简谐强迫激励,通过龙格-库塔法对CFRP斜拉索在主共振和亚谐波共振时的动力学行为进行了研究.研究结果表明,在强迫激励下CFRP斜拉索有较为丰富的非线性动力学行为.
1 CFRP斜拉索面内运动方程
斜拉索在风、桥塔和桥面激励作用下会产生大幅振动,给桥梁安全造成隐患.CFRP斜拉索由于其自重更轻、跨度更大,在风荷载作用下,其非线性动力学特性将可能更为突出.因此,对其非线性动力学特性开展深入系统的研究具有重要的理论和实际意义.对CFRP斜拉索的研究,特做以下基本假设:截面满足平截面假设、不考虑材料的非线性、将各向异性材料假定为横向各向同性、在重力作用下垂度曲线近似为抛物线.由于抗弯刚度对拉索的模态频率和相互作用(特别是高阶模态)有较大影响[12],因此,在动力学运动控制微分方程的推导过程中,考虑了CFRP拉索抗弯刚度和温度的影响.
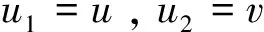
根据应变和位移的关系以及应力应变关系,可以得到CFRP斜拉索的势能为:
(1)

动能和外力做功分别为:
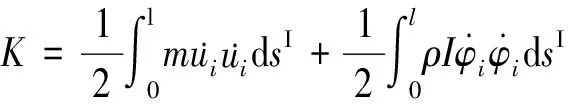
(2)

(3)
其中m为单位长度的质量;μi为拉索的黏弹性阻尼;ρ拉索的密度;pi为在x,y和z方向的分布荷载.
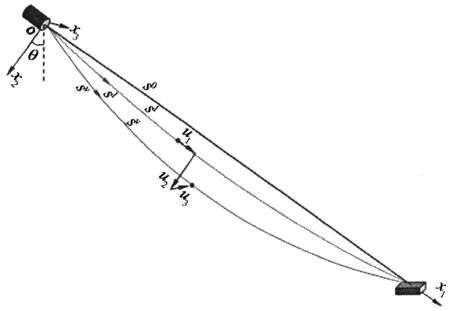
图1 CFRP斜拉索的静动态构形
根据Hamilton变分原理,

(4)
可得到CFRP斜拉索的空间运动偏微分控制方程为:
(5)
(6)

(7)

(8)

(9)
其中

(10)
由于拉索运动时纵向变形远小于其横向变形,且在考虑拉索低阶模态的横向振动时,横向模态和纵向振动模态不存在相互作用. 因此,忽略拉索的纵向惯性力、阻尼力和激励力的影响,方程(7)可以改写为:

(11)
考虑方程(10), 可以得到:

(12)
为研究拉索的面内强迫振动问题,忽略面外横向振动的影响和不考虑转动惯量的影响,由方程(5)和(8)可以得CFRP斜拉索面内运动的偏微分控制方程:

(13)
该方程通过退化处理可得到一般钢质拉索的非线性动力学运动控制微分方程.
2 无量纲化及Galerkin离散
引入以下无量纲量:
则方程(13)改写为:

(14)
类似地,式(12)改写为:

(15)
为研究CFRP斜拉索在强迫激励下面内一阶模态的振动问题,这里采用Galerkin方法对上述方程(14)和(15)进行处理.
假定振动函数:
v=φ(x)g(t)
(16)
则式(15)改写为:
ε(t)=B1g(t)+B2g2(t)
(17)
其中
将式(15)和(16)代入式(14),并进行Galerkin积分有:
a3g3(t)+f(t)=0
(18)
其中

式(18)即为CFRP斜拉索在强迫激励下的非线性振动常微分控制方程.
3 算例分析
以目前工程中最长拉索为基础设计CFRP斜拉索,CFRP斜拉索材料根据相关研究其纵向弹性模量Ex可在100~1 000 GPa变化,本文取Ex=137 GPa, 横向弹性模量为10.2 GPa.其余主要参数为:l=500 m,m=99.92 kg/m,A=0.001 718 9 m2,G=3.75 GPa,θ=22.5°,初始张拉力T0=570 t, 阻尼比取0.003. 进行无量纲参数分析时,在此基础上根据工程实际做适当变化.采用龙格-库塔法对常微分方程(18)求解,求得拉索在面内横向强迫激励下响应的时间历程图、相图、功率谱图和分叉图,从而对系统的非线性动力学特性进行研究. 为确保计算结果的正确,分叉图经过频闪法和Poincare截面法两种方法进行计算和相互验证.
图2为激励幅值f=0.001时,CFRP斜拉索稳态响应随激励频率变化的分叉图.从图中可以看出,随着激励频率的增大,系统经历了一个较为复杂的变化过程,总体表现为硬弹簧特性.当激励频率较小时(ω<0.026),系统表现出多周期小幅振动;在0.026<ω<0.175时,系统表现出单周期的稳态振动,但在此激励频率区间出现多次跳跃,响应幅值并不一定随着激励频率增大而增大,有时会逐渐变小;当激励频率大于0.118时,系统的响应幅值才随激励频率的增大而增大,当激励频率达到0.305时,通过单周期运动转换为多周期运动,同时响应幅值急剧减小,进入较为复杂的多周期运动;随着激励频率的进一步增加,多周期运动通过一小段的双周期运动过度为单周期运动,响应幅值进一步趋于零.

ω
图3为激励幅值f=0.002时,CFRP斜拉索稳态响应随激励频率变化的分叉图.与图2比较可以看出,由于激励幅值的增加,系统的响应变得越来越复杂,但总体上仍表现为硬弹簧特性.系统大幅振动的频率区间上限从0.305增大到0.343 5,当ω> 0.343 5时,系统进入混沌运动阶段,最后通过一小段频率带的双周期运动变为单周期运动.

ω
图4为激励幅值分别为0.003,0.004,0.005时,CFRP斜拉索稳态响应随激励频率变化的分叉图.从图中可以看出,不同激励幅值不能改变CFRP斜拉索的软硬弹簧特性,仍就表现出硬弹簧特性.随着激励幅值的增加,系统的分叉行为变得越来越复杂,当激励幅值达到0.005时,周期运动的频率区间越来越小,单周期稳态振动仅在0.118至0.130 5和0.137 5至0.229之间存在,其余频率域均变为多周期甚至混沌运动,混沌运动的频率区间变大.另外,拉索大幅响应的频率区间随激励幅值的增加也随之增大,同时响应的最大幅值也随之变大.
图5描述了在激励幅值为0.005时不同激励频率下CFRP斜拉索的时间历程、相图和功率谱图.从图中可以看出,在不同的激励频率下,系统表现出不同的运动状态,在激励频率为0.15时,系统处于混沌运动状态,形成连续谱成分,但以激励频率响应为主.当激励频率增大为0.17时,从相图和时间历程图可以看出系统做单周期稳态振动,但从功率谱图可以看出,其中仍含有较少成分的其它周期运动,并且这些离散谱峰倍频成分明显,只是对振动的贡献较小.这也说明结合多种方法分析系统的运动情况更为精确.激励频率增大到0.19时,系统表现出双周期运动.但是,与此同时也可以从功率谱图中观察到倍频成分,这些成分对振动的贡献几乎为零.

图4 系统随激励频率变化分叉图
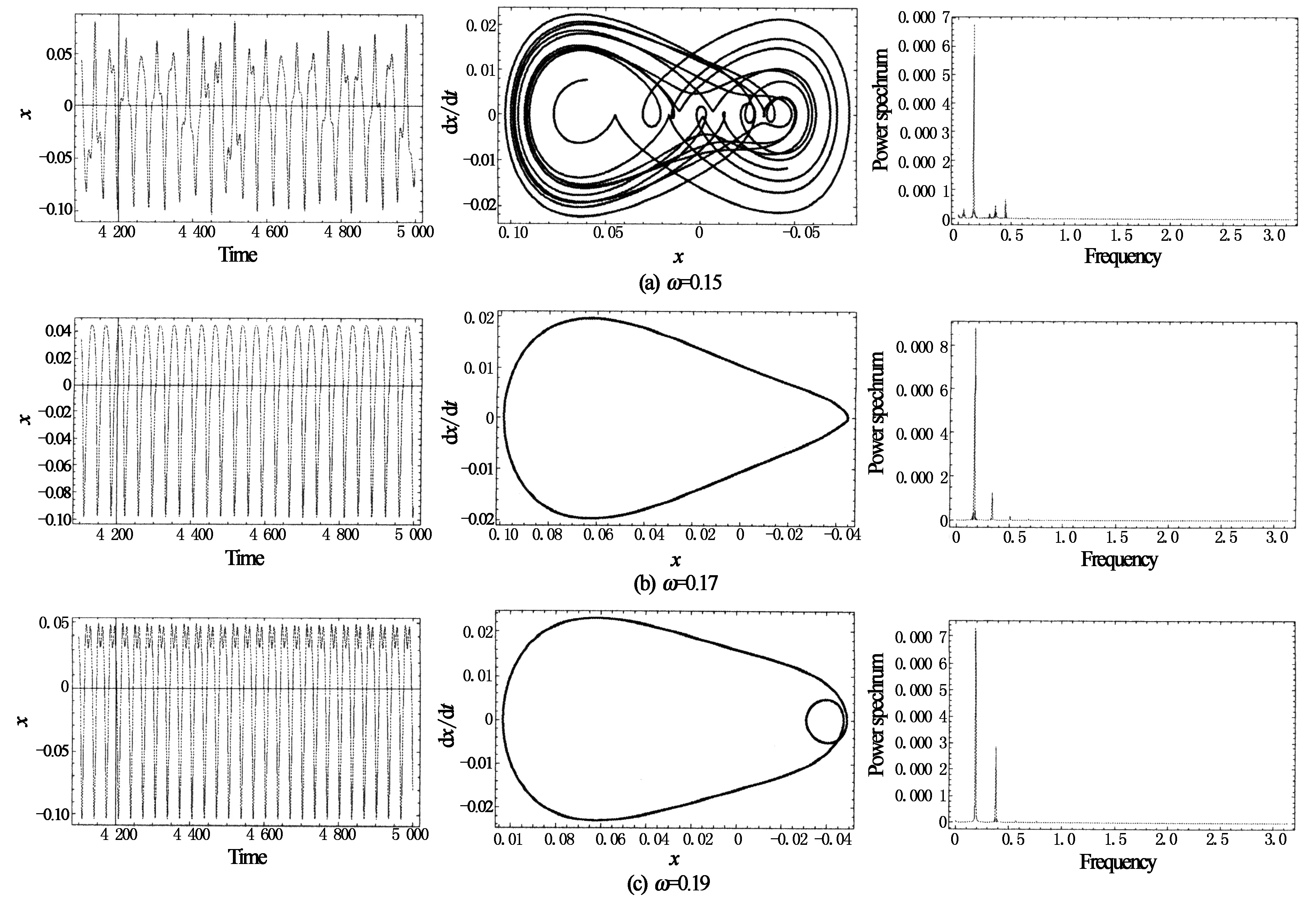
图5 不同激励频率时系统的时间历程、相图和功率谱图(f=0.005)
图6为主共振时系统随激励幅值变化的分叉图.可以看出,随着激励幅值的增加系统以单周期稳态振动为主,只在部分幅值区间出现多周期运动,如:双周期运动(0.000 74 图7为亚谐波共振时系统随激励幅值变化的分叉图. 比较图6可以看出,CFRP斜拉索在强迫振动情况下的亚谐波共振的响应幅值几乎都有一定程度的增大,但相对于发生参强激励的情况(亚谐波共振的响应幅值比主共振有数量级的提高)要小很多.由此说明,CFRP强迫振动时亚谐波共振和主共振的响应幅值在同一量级.从图7中可以看出,随着激励幅值的增加,单周期稳态振动的响应幅值同时增大.当激励幅值达到0.001 34时,系统的响应转变为双周期稳态运动,且响应幅值突然增大(响应出现跳跃现象).当激励幅值达到0.001 97时,双周期稳态运动再次转变为单周期运动.随着激励幅值的进一步增大,在0.004 058与0.004 203之间,由单周期运动转变为3周期运动,同时振动幅值伴有跳跃现象.当激励幅值大于0.004 203时,系统又回到稳态的单周期运动.最后,当激励幅值达到0.004 671时,系统转变为4周期运动,直到激励幅值达到0.003 24时,系统由4周期运动转变为8周期运动,进一步增加激励幅值,系统进入混沌运动.当激励幅值大于0.005 4时,系统突然由混沌运动转变为稳态的单周期运动. f f 通过对CFRP斜拉索面内强迫振动分叉行为的理论研究和算例分析,发现了丰富的非线性动力学现象,同时得到一些有意义的结论. 1)CFRP斜拉索面内强迫振动亚谐波共振的振幅虽然相对主共振时有一定程度的增加,但相对于参强共振时的情况,亚谐波共振危险性有可能和主共振为同一个量级. 2)通过对CFRP斜拉索面内响应随激励频率变化的分叉行为分析,系统具有非常丰富的非线性动力学特性:观察到了由倍周期分叉进入混沌的现象,最后混沌运动突然转变为双周期运动,进而转变为单周运动的现象. 3)当激励频率不变时,激励幅值越大,对应同一激励频率区间系统的运动可能会越来越复杂,同一激励频率下的单周期运动可能变为双周期多周期甚至是混沌运动. 4)在同一激励频率下,随着激励幅值的增大,CFRP斜拉索的响应幅值并不一定随着增大,可能在某一区间段响应幅值越来越小,最后可能通过跳跃行为,响应幅值突然有超过100%的增加. 5)亚谐波共振时,随着激励幅值的增加,发现CFRP斜拉索通过双周期分叉使响应幅值发生跳跃的现象,最后又转变为单周期稳态运动. [1]ACI. Prestressing concrete structures with FRP tendons[S]. MI,USA:Farmington Hills,American Concrete Institute. ACI,2004 . [2]ZHANG X J,YING L D. Aerodynamic stability of cable-supported bridges using CFRP cables[J]. Journal of Zhejiang University Science A, 2007,8(5):693-698. [3]张鹤, 谢旭. 车辆荷载作用下大跨度斜拉桥钢和CFRP拉索的非线性振动[J]. 工程力学, 2009,26(8): 123-130. ZHANG He, XIE Xu. Nonlinear vibration of steel and CFRP cables of long span cable-stayed bridge under vehicular loads[J]. Engineering Mechanics, 2009,26(8): 123-130 .(In Chinese) [4]谢旭,张鹤,朱越峰,等. CFRP拉索在横向风荷载作用下的振动特性[J].浙江大学学报:工学版,2008, 42(1): 145-151. XIE Xu, ZHANG He, ZHU Yue-feng,etal.Dynamic characteristics of CFRP cables under lateral wind load[J]. Journal of Zhejiang University: Engineering Science, 2008, 42(1): 145-151. (In Chinese) [5]谢旭,张治成,中村一史,等. 考虑脉动风影响的斜拉索在支点激励下的非线性振动[J]. 土木工程学报, 2008,41(12): 66-72. XIE Xu, ZHANG Zhi-cheng, NAKAMURA H,etal. Nonlinear vibration of stay cables under fluctuating wind load and support excitation[J]. China Civil Engineering Journal, 2008,41(12): 66-72 .(In Chinese) [6]XIONG W, CAI C S, ZHANG Y,etal. Study of super long span cable-stayed bridges with CFRP components[J]. Engineering Structures,2011,33:330-343. [7]FANG Z, FAN F, REN L. Performances of super-long span prestressed cable-stayed bridge with CFRP cables and RPC girder[J]. Engineering Sciences, 2013,11(5): 70-76. [8]梅葵花,陆志涛,孙胜江. CFRP拉索的非线性参数振动特性[J]. 中国公路学报, 2007,20(1):52-57 . MEI Kui-hua, LU Zhi-tao, SUN Sheng-jiang. Property of nonlinear parametric vibration of CFRP cables[J]. China Journal of Highway, 2007, 20(1): 52-57. (In Chinese) [9]吴晓,杨立军,孙晋. 碳纤维缆索悬索桥竖向非线性自由振动研究[J]. 动力学与控制学报, 2010,8(1): 67-73. WU Xiao, YANG Li-jun, SUN Jin. Vertical nonlinear free vibration of suspension bridges using carbon fiber cables[J]. Journal of Dynamics and Control, 2010,8(1): 67-73. (In Chinese) [10]KANG H J, ZHU H P, ZHAO Y Y,etal. In-plane non-linear dynamics of the stay cables[J]. Nonlinear Dynamics, 2013,73(3): 1385-1398. [11]李志江. 碳素纤维复合材料(CFRP)斜拉索非线性振动特性和参数激励研究[D]. 武汉:华中科技大学土木工程学院, 2011:20-60. LI Zhi-jiang. Study on nonlinear vibration properties and parametric excitations of CFRP stayed cables[D]. Wuhan: School of Civil Enginering & Mechamics,Huazhong University of Science and Technology,2011:20-60.(In Chinese) [12]赵跃宇,周海兵,金波,等.考虑弯曲刚度的斜拉索内共振分析[J]. 湖南大学学报:自然科学版,2007,34(5): 1-5 . ZHAO Yue-yu, ZHOU Hai-bing, JIN Bo,etal.Internal response of inclined cable considering bending rigidity[J]. JournaI of Hunan University: Natural Sciences, 2007,34(5): 1-5.(In Chinese)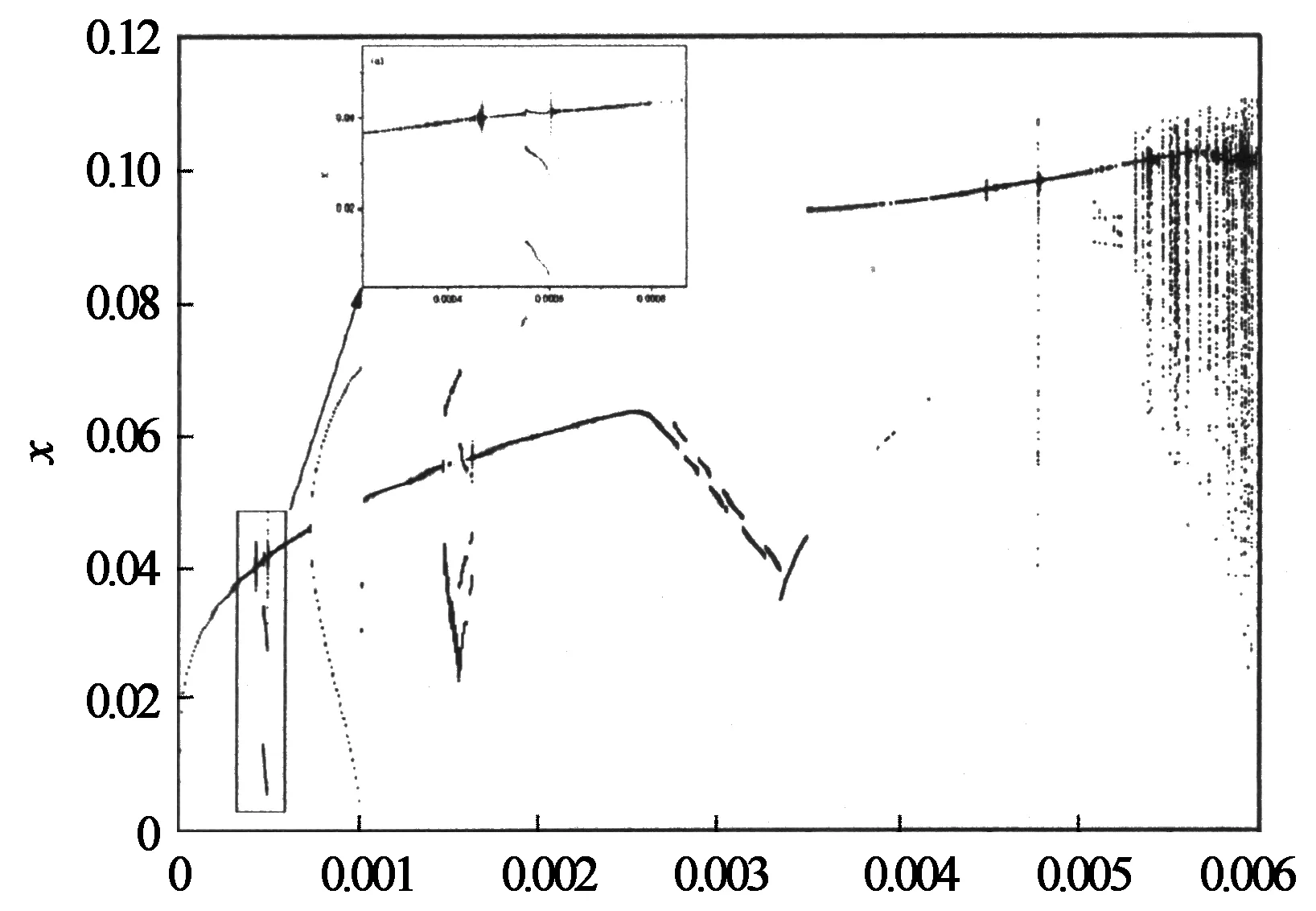

4 结 论

