相对论效应在分子结构教学中的案例分析*

张晨曦 王彦茗 杜俊 王雪峰

(同济大学化学系 上海200092)

量子力学和相对论是近代微观物理世界的两大支柱。因此，包含相对论效应的量子力学是了解化学现象尤其是分子结构的理论基础。由于现代量子化学计算的迅猛发展以及对重金属元素(如Au、Ru、Rh以及Pd等)催化过程的深入研究，重元素及其化合物的许多“反常”现象均需要用相对论效应给予合理的解释。之前有关相对论效应的讨论主要集中于量子化学计算方法的讨论［1］、光谱性质［2］、惰性电子对、镧系收缩以及Au和Hg物理性质的介绍［3］。就笔者所知，目前国内教科书中还没有针对相对论效应在重金属分子构型的影响进行讨论。

本文首先介绍相对论效应对成键轨道的影响;其次，在之前研究工作的基础上［4］，选取第ⅥB族金属氢化物为研究对象，讨论相对论效应对第ⅥB族金属氢化物结构变化趋势的影响以及UH6正八面体构型的成因。希望通过本文的探讨，能够使学生认识到利用相对论效应这一基本物理学规律，可以帮助解释许多过渡金属化合物结构及成键中的“反常现象”。

1 相对论效应简介

1.1 直接相对论效应

离核越近的电子受到核的吸引越强，其平均速度越大;当其平均运动速度较光速不能忽略时，其相对论效应便越发显著。相对论效应引起核外电子的质量增大，轨道半径相应减小，能级减小。以Au为例，其1s电子由于相对论效应的影响，m=1.23m0。由于1s轨道的玻尔半径和质量m成反比，随着m增大，Au的1s轨道半径减小近20%。按照原子轨道的正交性，1s轨道收缩，必然引起2s、3s、4s、5s以及6s等n s轨道收缩，其能级也相应减小。

1.2 间接相对论效应

因为对称性的差异，n s轨道的收缩不会引起d、f等轨道的收缩。相反，收缩的s轨道会增加对核的屏蔽效应，使穿透本领很低的外层d和f轨道有效核电荷减小。因此，和无相对论效应相比，d和f轨道径向分布出现膨胀，能级升高。外层d和f轨道的相对论性膨胀与外层s轨道的相对论性收缩差不多一样大小［6］。与此同时，外层d和f轨道的膨胀削弱了它们自身的屏蔽作用，增大了外层s轨道的有效核电荷，进一步促进了s轨道的收缩。

从上述讨论可以得出，直接相对论效应与间接相对论效应相互促进，在价层电子成键过程中:外层s轨道收缩，能级降低;内层d、f轨道膨胀，能级升高。随着原子序数增大，相对论效应对成键和分子结构方面的影响越发显著，分子构型会出现一些反常性质。下面使用相对论效应解释其对第ⅥB族金属氢化物结构变化趋势的影响以及UH6正八面体构型的成因(图1)。

2 相对论效应在杂化轨道理论中的应用

随着现代量子化学的发展和计算机计算水平的提高，目前对重金属化合物结构与性质的讨论通常使用量子化学计算的方法进行。本文选取第ⅥB族金属氢化物对其分子结构进行讨论，一方面由于第ⅥB族金属氢化物的分子结构已有详实的理论和实验研究，大量的计算数据可供参考，另一方面由于氢作为配体不包含孤对电子，可以不考虑配体间的相互排斥作用，因而其分子构型可以较好地反映中心原子杂化轨道的形状，有利于成键分析。

笔者曾讨论了WH6畸变三角锥构型的成因(图2)［4］:由于d轨道参与成键轨道杂化，使得原先规则的sp等性杂化向畸变的sd不等性杂化轨道转变［7-8］。杂化是指原子在化合生成分子的过程中，根据原子成键的要求，在周围原子影响下将原有的原子轨道进一步线性组合成新的分子轨道的过程［9］。杂化轨道的形成需要满足一个基本条件:只有能量相近的轨道才能发生杂化［10］。参与杂化的s，p，d等成分若相同，则称为等性杂化;若不相同，即不等性杂化。其中，不等性杂化成因有两类，一是由于在参与杂化的轨道中含有成对电子对，例如NH3中心原子N为sp3不等性杂化，有一个杂化轨道的能量较低，被一对孤对电子所占据，另外3个杂化轨道能量较高，为单电子所占据。另一类是由于参与杂化的原子轨道能量差异较大，为满足各个轨道最大程度参与成键，形成了不同等性杂化轨道间的组合［9］。本文主要探讨不含孤对电子时相对论效应对杂化轨道的影响。

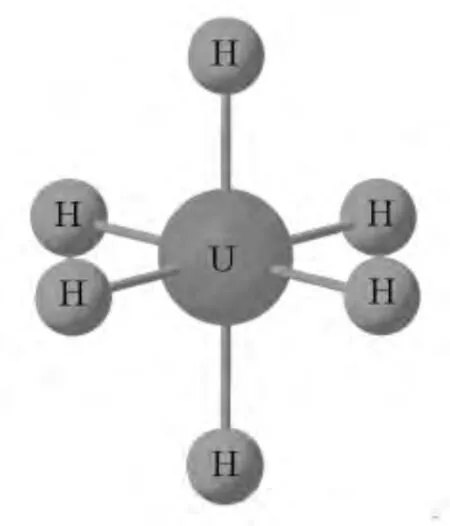
图1 UH 6的Oh构型

图2 WH 6的C3v构型

在教学中所涉及的杂化轨道一般局限于主族元素中，仅是s和p轨道之间的杂化。由于相邻的s和p轨道之间的能量差较小，形成的sp杂化轨道一般是等性的。然而，进入过渡金属区域后，杂化轨道转变为sd杂化，由于相邻s轨道和d轨道之间的能量差较大，所有轨道无法形成等性杂化。以下讨论中所罗列的计算数据均来自近期高水平量子化学计算结果［11-13］。

对于6配体的分子构型，正八面体结构(Oh)对称性最强，属于典型的等性杂化;与此对应，畸变的C3v分子构型通过不等性杂化满足第ⅥB族金属d轨道最大程度成键。因此，能量较高的Oh构型与稳定构型C3v之间的能量差可以直观地反映出中心原子产生等性杂化的难易程度。由表1可得，由Cr到Mo规则构型与畸变构型的能量差增大，而从Mo到W规则构型与畸变构型的能量差却减小。这说明了在Cr、Mo和W 3个过渡金属中，Mo中心原子最难形成等性杂化，也表明4d与5s轨道间能量差最大。

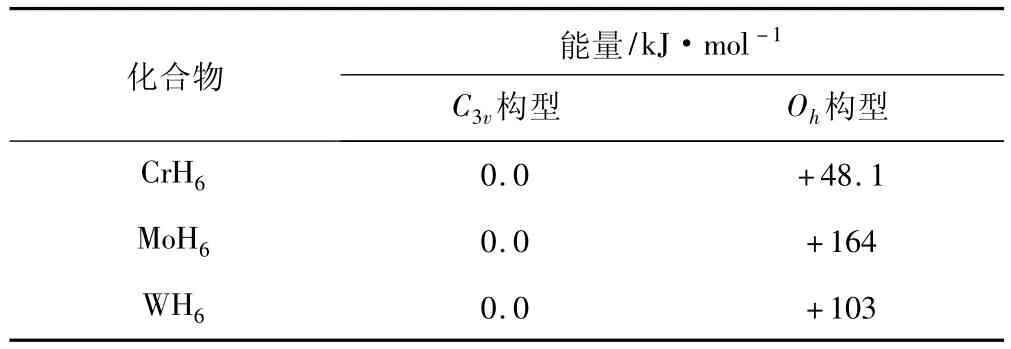
表1 第ⅥB族金属氢化物C3v与Oh构型能量对比

相对论效应可以合理解释这一现象:在同一族元素中，由于受到屏蔽效应及钻穿效应的综合影响，随着周期数增大，s和d轨道之间的能量差也随之增大。这可以合理地解释Mo的4d与5s轨道间能量差大于3d与4s轨道间能量差。然而，随着原子序数增大，相对论效应越发明显。6s轨道由于直接相对论效应，轨道收缩能级降低;与此同时，5d轨道由于间接相对论效应，轨道膨胀能级升高。两者的相互作用使6s与5d轨道间的能量差小于5s与4d轨道间的能量差。因此，W相比Mo来说更容易实现等性杂化。对比分析可知，由于相对论效应使6s轨道收缩而5d轨道膨胀，两者之间的能量差减小，杂化更为容易，其杂化形式由不等性杂化逐渐趋向于等性杂化。

第ⅥB族金属氢化物畸变构型(C3v)的成因在于最大程度满足d轨道成键，以使整个体系的能量最为稳定。由表2可知，NBO分析表明Mo的d轨道含量最大，这也可以合理地解释MoH6的Oh构型与C3v构型能量差最大。由于相对论效应的影响，d轨道膨胀而能级升高，s轨道收缩而能级降低。这使s轨道更容易参与杂化轨道成键。对比分析包含和不包含相对论效应的WH6中心原子W的成键也可以看出，相对论效应提高了s轨道的含量而降低了d轨道的参与程度。

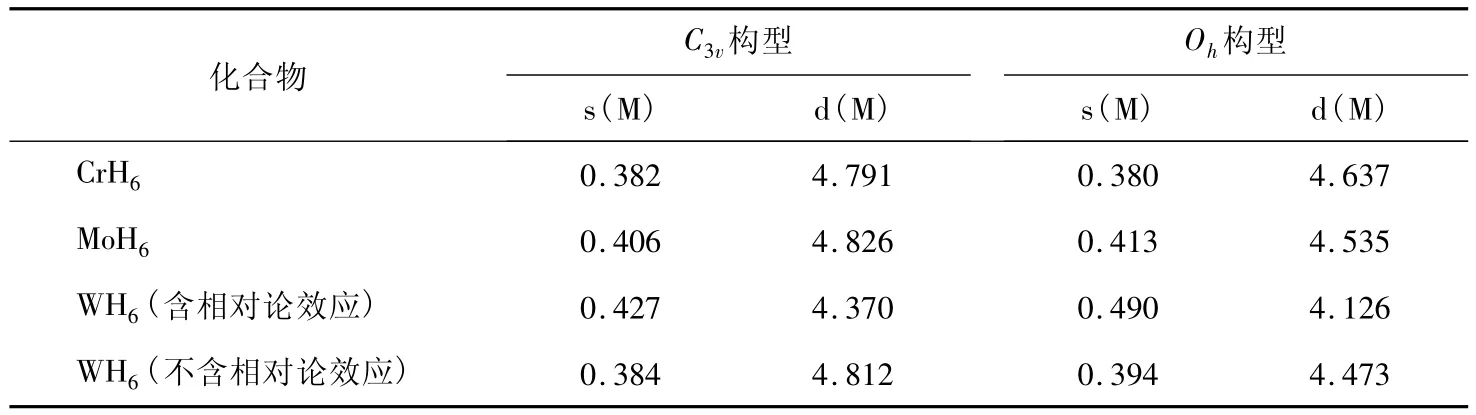
表2 第ⅥB族金属氢化物C3v与Oh成键分析

另一极端的例子是UH6。U的原子序数为92，相对原子质量高达238，因此，其相对论效应更为显著。对于UH6分子(图1)，在实验中还很难观察到其最为稳定的构型，但是通过量子化学计算(表3)，得到其稳定构型为正八面体(Oh)。由于H配体不含孤对电子并且与中心原子形成σ键，因此，Oh构型很好地反映了中心原子U的杂化形式。对于UH6分子而言，在以下两个方面与WH6不同:一是由于相对论效应在此非常明显，s轨道收缩能级降低并且d和f轨道膨胀能级升高，形成杂化轨道的能级差减小，杂化更为充分，呈现出等性杂化。另外，中心原子的杂化方式不同。U原子含有f轨道参与杂化，并使其最大程度重叠。由于f轨道的伸展不同于花瓣状的d轨道，其杂化轨道的形状趋于正八面体的规则构型。

表3 UH 6能量与成键分析

3 结语

由上述分析可知，不等性杂化并不是仅仅存在于含有未成键孤对电子的分子，第ⅥB族氢化物的C3v构型正是很好的不等性杂化的案例，由于3d和4s轨道的能级差距较大，出现了能级分裂的情况，形成了上下不对称的杂化轨道形状以使d轨道最大程度成键。另外，相对论效应在重金属成键过程中起到了举足轻重的作用。相对论效应在化学结构与成键方面的主要作用是s轨道的收缩与d、f轨道的膨胀，使s与d、f轨道的能级更为接近，使得各个轨道间杂化更为容易并且使得第ⅥB族金属氢化物由不规则的不等性杂化向规则的等性杂化转变。

［1］戴树珊，马忠新.化学通报，1988(9):1

［2］冯平义，王岩，廖沐真.化学通报，1998(5):25

［3］周公度.大学化学，2005，20(6):50

［4］张晨曦，王雪峰.大学化学，2012，27(4):79

［5］周公度.大学物理，2005，24(12):8

［6］严成华.化学通报，1983(1):42

［7］Kaupp M.Angew Chem Int Ed，2001，40:3534

［8］Bayse C A，Hall M A.J Am Chem Soc，1999，121:1348

［9］周公度，段连运.结构化学基础.第4版.北京:北京大学出版社，2007

［10］宋天佑，程鹏，王杏乔.无机化学(上册).北京:高等教育出版社，2004

［11］Straka M，Hrobarik P，Kaupp M.J Am Chem Soc，2005，127:2591

［12］Tanpipat N，Baker J.J Phys Chem，1996，100:19819

［13］Kaupp M.J Am Chem Soc，1996，118:3018