一种基于NSCT和PCNN的图像融合算法

石瀚洋，杨 静，赵 焱

(太原理工大学信息工程学院，山西太原 030024)

图像融合是信息融合的重要组成部分，它帮助研究人员得到更清晰、可靠、高理解度的高质量图片，是图像处理的基础。随着电子技术和传感器技术的快速发展，图像融合技术在医疗、生物、工程检测、军事、等方面都发挥了重要的作用。近年来，在目标识别、人脸识别、目标检测、目标跟踪、医疗成像、对地观测和计算机视觉等领域更是如此。图像融合是将两个或两个以上的传感器在同一时间或不同时间获取的关于某个具体场景的图像或图像序列信息加以综合，以生成新的有关场景解释的信息处理过程［1］。图像融合通常在像素级、特征级和决策级三个层级中展开［2］。其中，像素级融合是核心也是基础。

在图像融合的诸多方法中，基于多尺度分解的图像融合尤为重要。其中，小波变换的时－频特性优良，展现出很好的多分辨率特性。可需要说明的是，其分解出的方向特性信息有限(横向、纵向和对角线方向)。因此，在研究者们通过不断的努力下，新的图像尺度分解方法不断被提出(如脊波变换、曲波变换)这些图像变换方法都有各自的优点，可是应用效果总是不尽如人意。Do等人在2002年提出了Contourlet变换［3］，解决了方向性和多分辨率特性的问题，是一种有效的图像多尺度表示方法。研究证明基于Contourlet变换的融合算法是优于上述那些算法的。但是下采样被应用在变换过程中，使其没有体现出平移不变性。这会使得伪吉布斯现象出现，从而影响融合效果。由A.L.Cunha于2006年等提出的NSCT(Nonsubsample Contourlet Transform)改变了这一局面，它不但与Contourlet变换一样，拥有多尺度、多方向特性，它还具有平移不变性，这样从根本上消除了伪吉布斯现象。

PCNN是上世纪末Eehorn等提出的第三代人工神经网络神经网络，它是模拟猫大脑皮层的生物学特性提出的，它具有全局耦合性和脉冲同步性，对图像的每个像素的特性与全局特性能够做到兼顾。本文在分析NSCT的基础上，针对多聚焦图像在融合时需要着重考虑清晰度的问题，将NSCT和PCNN组合应用，在NSCT变换域提出基于PCNN和清晰度融合规则相结合的多聚焦融合方法。

1 非下采样Contourlet变换(NSCT)

NSCT是由Contourlet变换改进衍生而来的，它具有Contourlet变换所见长的多尺度、多方向特性。与此同时，为了防止伪吉布斯现象的出现，NSCT采用非下采样金字塔(NSP)分解和非下采样方向滤波器组(NSDFB)来实现逐层的图像分解。NSP分解在低通分量上进行，每一级都获得一对子带图像(低通子带图像和高通子带图像)。由此，图像在通过级NSP分解之后，一共得到了1个低通和k个高通图像，共k+1个子带图像被分解出来，这组子带图像的尺寸和大小与源图像相同。NSDFB是一组二通道非采样滤波器组，频率响应特性为扇形。它的构建基础是在Bamberger所设计的扇形方向滤波器组。与后者不同的是，前者移除了方向滤波器组中的下采样部分。如果对某子带图像做n级方向分解，2n个方向子带图像可以被得到，这些图像的尺寸和大小同样与源图像相同，如图1所示。

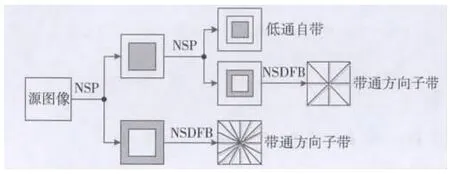
图1 NSCT分解示意图

2 脉冲耦合神经网络(PCNN)

PCNN是一个神经网络，它是由多个神经元组成的。由于PCNN相对复杂，人们提出了一些简化模型。但是，无论如何简化，接收域、制域调和脉冲产生器是每个神经元必须包括的3个部分。本文采用的是其中一种简化模型［4］

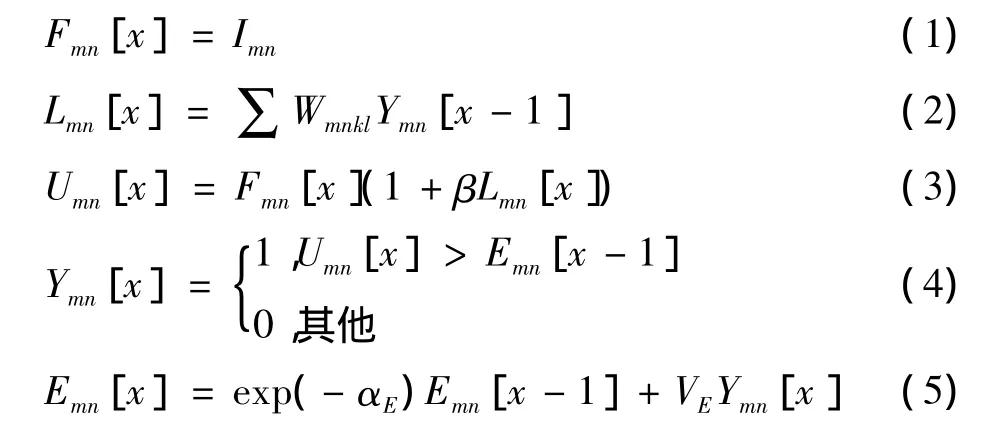
式中:I为输入激励，通常是点(i，j)的像素灰度值，每个像素对应一个神经元;F是神经元的输入部分，L是连接输出;U对应神经元内部活动项;Y是输出;E为动态阈值;W是神经元的内部连接矩阵。在此简化模型中，有4个参数 W，β，aE，VE，其中，神经元 (i，j)同神经元 (k，l)的连接权Wijkl取值为

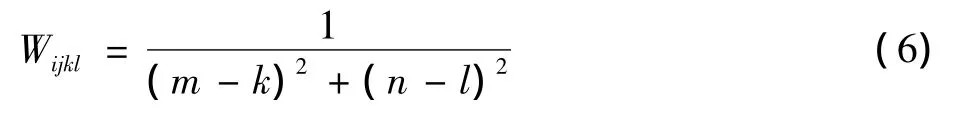
PCNN的整个工作过程为:脉冲输出在某个神经元发生时，这个神经元的动态门限会突然增大，这样脉冲输出不会在第二次输入时产生，于是门限开始衰减。一旦其内部活动项大于不断衰减的门限值时，就会再次产生脉冲和周期变化。这里脉冲产生被研究者称为点火。

3 基于清晰度和PCNN的NSCT多聚焦图像融合

3.1 融合步骤

首先，通过NSCT分解对待融合图像进行处理，然后对低频信息和高频信息分别融合处理。融合规则充分考虑到多聚焦图像的特点，最大限度地保留待融合图像的互补信息以及特有信息，可以得到更高的融合质量。最后在NSCT反变换后得到融合图像(见图2)。

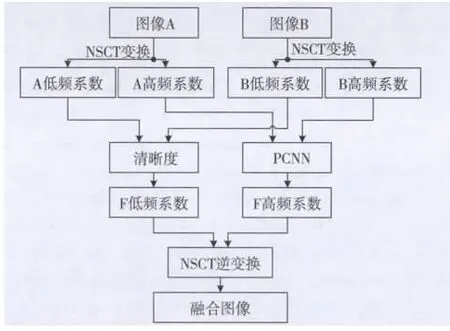
图2 本文算法流程图

具体融合过程如下:

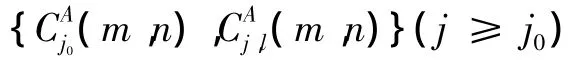
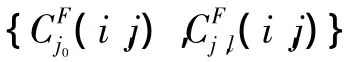
3)对融合后的系数进行NSCT逆变换，算法结束，获得融合结果F。

3.2 低频子带系数融合规则

图像的低频部分集中了图像的主要能量。目前的低频子带融合规则一般包含简单的平均法、绝对值取大法、区域能量法等。由于这些方法没有同时考虑到图像的清晰度信息和边缘信息，所以就会在一定程度上损失图像的信息，降低图像的清晰度和对比度，影响融合图像的视觉效果。因此，本文对低频子带系数提出一种结合文献［5］和文献［6］的融合规则。

1)对源图像A的低频子带系数定义一个变量EA，称之为边缘区域能量

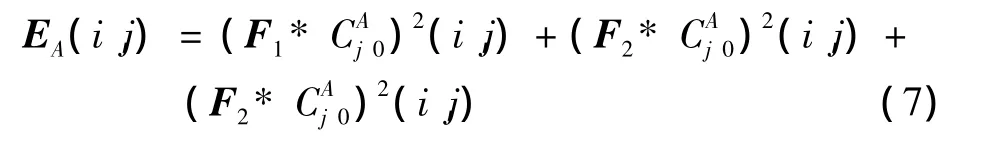
同时，对图像B定义变量EB，变量E反映了图像的边缘综合信息，其方向为水平、垂直和对角线方向。

2)根据清晰度的概念给出局部清晰度G(m，n)。

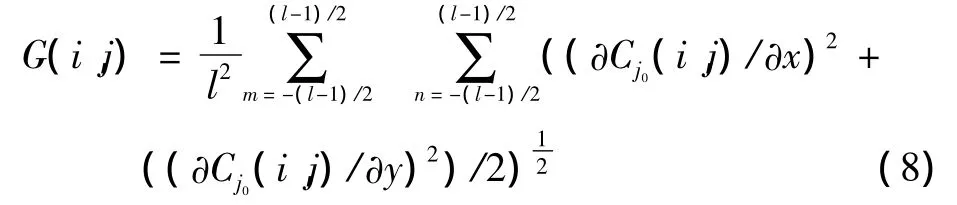
式中:∂Cj0(i，j)/∂x，∂Cj0(i，j)/∂y)分别表示点 (m，n)处沿x，y方向的微分，在图像中表示为相邻像素系数的变化率。l×l为以点(i，j)为中心的区域大小，本文取3×3的正方形区域。

3)经过下式判别得到融合后的判别因子

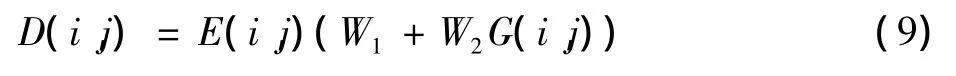
式中:W1，W2为大于0的常数，用来调整两项指标的权重，本文取W1=0，W1=1 。

本文低频子带系数选用判别因子D较大的尺度系数，让边缘和清晰度信息得以最大程度地在融合图像中体现。融合函数表达为

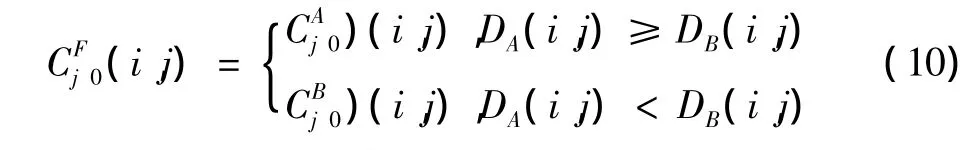
3.3 高频子带系数融合规则

高频系数在图像中所对应的是细节信息(如边缘和纹理)，人眼对这部分的信息识别最敏感，所以高频融合规则的选取显得尤为重要。为了使源图像的特征信息得以充分保留，本文应用基于自适应PCNN的融合方法对高频系数进行处理。融合过程如下:

1)分解最高层分尺度J以外的其他J－1层，本文选用高频系数作为PCNN的触发神经元。空间频率与图像的活跃程度有着成正比的关系，也就是说，图像越清晰，那么它的空间频率也就越大。本文对对应的神经元的链接强度采取应用拓延后的空间频率［7］方式。这种空间频率定义为

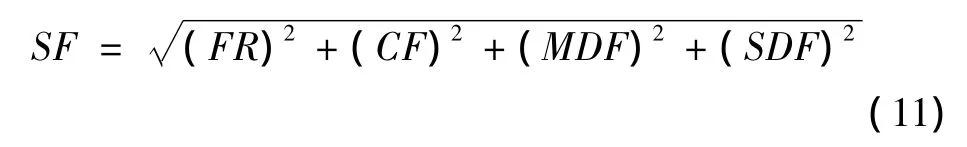
式中:RF为行频率，CF为列频率，MDF表示主对角频率，SDF表示次对角频率。

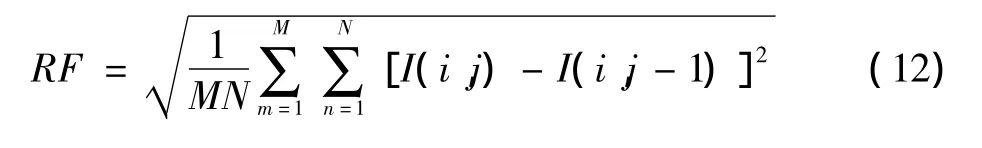
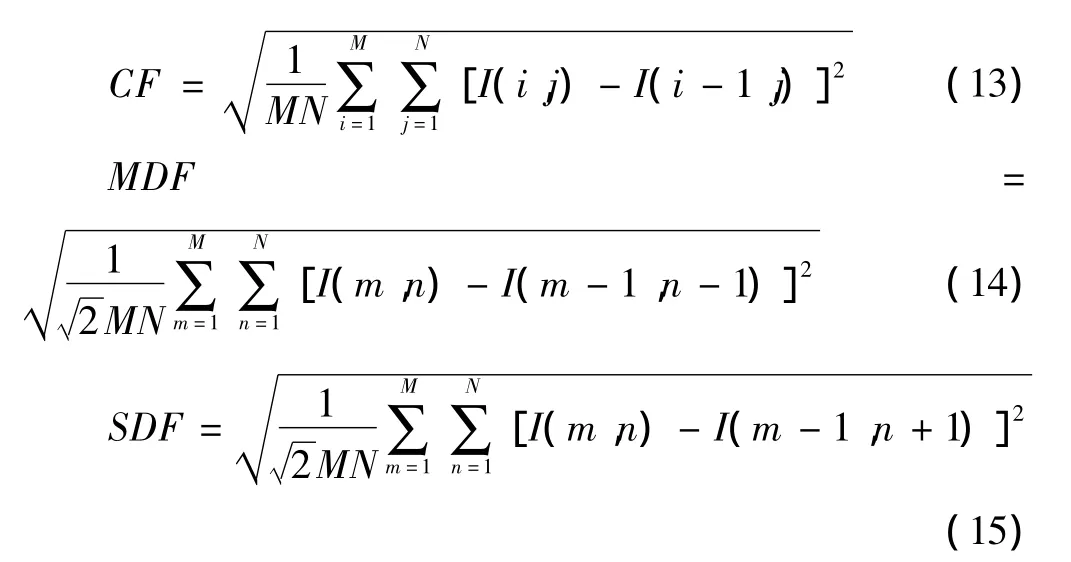
在PCNN系数中，链接强度β对于图像融合起到关键的作用，其余参数的影响不大。链接强度表示为

式中:η为大于零的常数，用于调节β的取值。

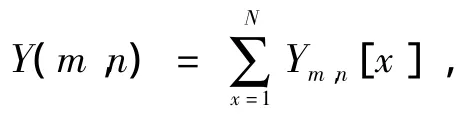
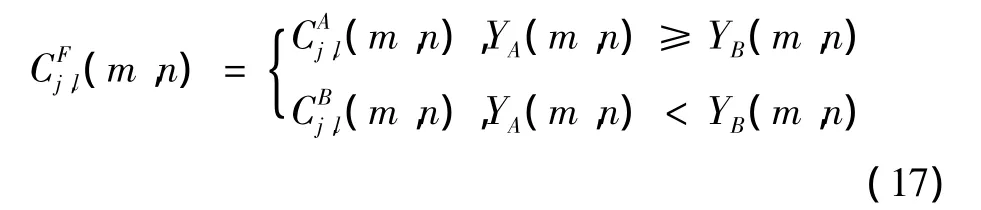
2)分解最高层分尺度J的高频系数，本文采用系数绝对值取大法

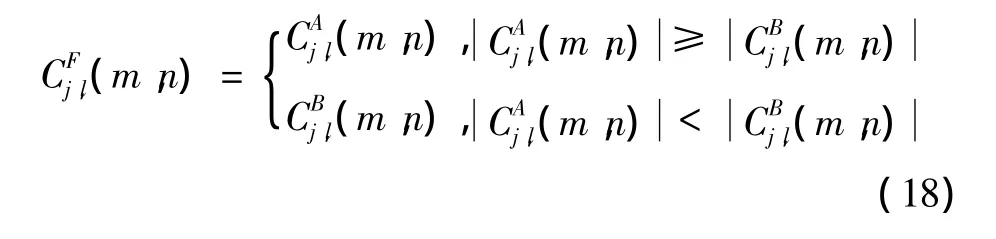
4 实验结果分析

4.1 融合实验

本文在MATLAB7.0环境下，实验数据采用PEPSI左右聚焦测试卡的图像，图像灰度为256级，大小为512×512，对本文提出的融合方法进行融合实验，其中a=0.1，V=20，N=2 000。同时与目前常用的几种融合方法进行了对比实验，以证明本文方法的优越性。方法一为小波变换融合，方法二为Contuorlet变换融合，方法三为NSCT简单融合，其主要融合方法为简单的系数取大法、均值法、区域方差法。公式实验结果见图3。

4.2 融合结果评价

主观评价:从视觉效果来看，方法一视觉效果模糊，不能分辨出右上角字迹，右边条形码严重失真;方法二视觉效果明显提高，字迹依稀可见，但是不够清晰;方法三可以很容易地辨认出右上角与罐体上字迹，但是字迹边角不够圆滑。本文方法实验效果最好，罐体上和测试卡清晰可见，字迹圆滑，条形码可以清晰辨认。

图3 融合图像实验图

客观评价:本文选用信息熵、清晰度、交叉熵、平均梯度4个评价参数对以下几种方法的图像融合性能做出了定量的比较，如表1所示。

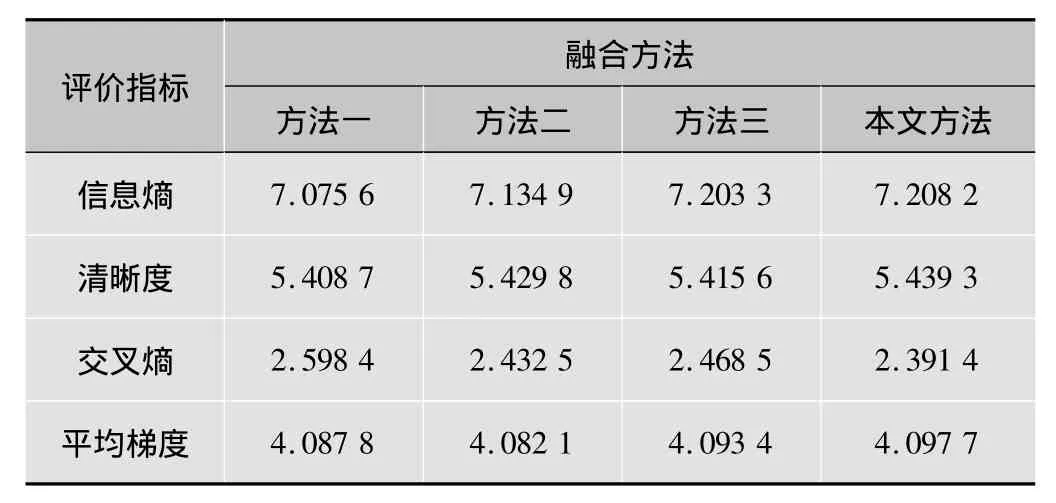
表1 多聚焦图像不同融合算法性能比较

表1可以看出，本文算法大部分指标优于对比融合算法。其中，平均梯度、信息熵和清晰度越大，图片质量越好，交叉熵越小，图片损失的信息越少，图片质量越好。从4种评价指标来看，本文方法是4种方法中最好的。

结合主观和客观两个方面，说明本文算法是一种可行的融合方案。

4.3 与近年研究比较

近年来有许多文献对以NSCT－PCNN为基础的图像融合方法进行了研究［8－10］，它们都有自己的特点和不足，其中文献［8］的方法没有采用拓延的空间频率，不能体现对角线方向的图像信息;文献［9］的方法在低频分量没有兼顾边缘信息和清晰度;文献［10］的方法没有对PCNN作自适应处理，使得PCNN参数需要凭经验配置。

5 结束语

针对清晰度的高低反映了多聚焦图像融合的融合效果好坏的特性，在NSCT变换域提出了一种基于清晰度和PCNN的融合算法。在对2幅图像进行NSCT变换之后，应用本文的算法对不同的子带系数进行融合处理。然后对上述处理后的系数进行NSCT逆变换，得到最终的融合结果。最后对本文提出的算法进行主客观的分析。实验表明，本文算法无论从主观还是客观，均比常用算法的融合质量好，使得融合后的图像清晰度提高。

:

［1］敬忠良，肖刚，李振华.图像融合理论与应用［M］.北京:高等教育出版社，2007.

［2］吴仰玉，纪峰，常霞，等.图像融合研究新进展［J］.科技创新导报，2013(1):49－54.

［3］DO M N，VETTERLI M.The contourlet transform:an efficient directional multiresolutionimage representation［J］.IEEE Transactions on Image Processing，2005，14(12):2091－2106.

［4］苗启广，王宝树.一种自适应PCNN多聚焦图像融合新方法［J］.电子与信息学报，2006，28(3):466－470.

［5］晁锐，张科，李言俊.一种基于小波变换的图像融合算法［J］.电子学报，2004，32(5):750－753.

［6］王俊文，刘光杰，戴跃伟，等.基于非抽样Contourlet变换的图像模糊取证［J］.计算机研究与发展，2009(9):1549－1555.

［7］ZHENG Y，ESSOCK E A，HANSEN B C，et al.A new metric based on extended spatial frequency and its application to DWT based fusion algorithms［J］.Information Fusion，2007，8(2):177－179.

［8］傅圣雪，林忠宇.基于NSCT_PCNN算法的雷达图像融合研究［J］.现代电子技术，2012，35(12):82－86.

［9］符强，任风华，纪元法，等.基于NSCT和自适应PCNN的遥感图像融合方法［J］.计算机测量与控制，2012，20(5):1344－1346.

［10］李红，吴粉侠，赵蔷.基于NSCT与PCNN的图像融合［J］.航空计算技术，2013，43(1):58－64.