Multi－h CPM信号的减少状态多符号差分非相干检测

钟 声，谢顺钦，张 健，杨 春

(中国工程物理研究院电子工程研究所，四川绵阳 621900)

多指数连续相位调制(Multi-h CPM)是一种有记忆的、高效的、恒包络的非线性调制技术，它所具备的高效频谱效率，并且对功放和信道的非线性特性不敏感等性质，使其在无线通信系统和数字卫星广播通信系统中有着广泛的应用前景［1-3］。若干随时间循环变化的调制指数不仅可以提高抗误码能力［4］，还可以使频谱更加紧凑、带外滚降更快，提高其频谱利用率。在带宽和功率受限的条件下，Multi-h CPM有着比单指数CPM更加优异的传输性能。但随着进制数、部分响应长度、调制指数数量的增加，使得接收端的网格状态数和匹配滤波器数都呈指数形式增加，同时Multi-h CPM特殊的表达形式使得其载波相位恢复困难且算法复杂度较高。因此，在降低实现复杂度的同时如何有效地避免载波相位对Multi-h CPM信号检测的影响成为了Multi-h CPM研究的关键。文献［5］给出了一种基于复合网格处理的CPM信号的非相干检测算法，通过在复合网格图的单元网格之间引入状态耦合转移，实现了对载波初相和频偏的跟踪，但是引入复合网格图增加了实现复杂度。文献［6］给出了Turbo码与CPFSK级联的SCCPM的非相干检测算法，通过迭代译码提高了CPM信号的检测性能。文献［7］研究了CPM信号的多符号分组的非相干检测算法，通过以连续多个符号为观察窗计算分支度量的增量以完成CPM的检测。文献［8］给出了二进制CPM的多分支多比特差分检测算法，通过对不同分数比特区间差分信号合并判决改善了信噪比，但是该算法不适用于多进制的Multi-h CPM信号。

本文提出了一种适用于Multi-h CPM信号的减少状态多符号差分非相干检测算法，通过对接收信号前后码元符号差分消除了载波初相对解调影响的同时，引入了参考相位信号，实现了对残留载波频偏的校正，然后结合逐幸存处理技术(Per-Survivor Processing，PSP)利用网格上每个网格状态对应的幸存路径上的假设判决码元信息估计出维特比算法中影响分支度量计算的未知状态项，从而减少了网格状态数，使得接收端能以较小的性能损失获得复杂度的降低。并且通过利用搜索维特比译码时不同调制指数序列所对应的分支度量实现了接收端调制指数估计与同步，而不需要额外的调制指数同步模块，从而简化了Multi-h CPM接收机的结构，有利于系统的实现。最后给出了文章算法的计算机仿真验证结果。(为便于表述，下文中x～和^x分别表示x的假设值和估计值，*表示求共轭，H表示求共轭转置，Re(·)表示求实部)

1 Multi-h CPM信号模型

Multi-h CPM的复基带解析式为

2 差分非相干序列检测

2.1 接收信号模型

假设信道为高斯加性白噪声信道，则经过数字下变频、载波频偏校正和符号定时同步后接收的Multi-h CPM信号的复基带可以表示为

式中:n(t)为功率谱密度为N0的零均值复高斯白噪声;θ0为信道引入的载波初相(对某次接收而言，θ0的取值固定);φ(t)为数字下变频和载波频偏校正后的残留载波频偏Δf所引入的时变载波相位，且φ(t)可以表示为

式中:τ表示时间增量［9］。

2.2 分支度量的计算

在非相干检测中，常用前后符号差分消除载波初相和部分残留载波频偏对解调的影响。对于Multi-h CPM信号，一方面通过增加差分间隔的符号数量可以减小噪声对差分非相干检测的随机性干扰从而提高其检测性能，另一方面差分间隔的符号数的增加使得实现复杂度呈指数形式增加的同时又人为地增加了其部分响应长度，从而造成对多符号差分检测相对1符号差分检测对残留载波频偏更加敏感，后续的仿真结果也验证了这一点。因此，本文主要研究Multi-h CPM信号的1符号差分检测和2符号差分检测。

接收信号r(t)经过N符号间隔差分后的差分信号可以表示为

式中:nNd(t)为N符号间隔差分后产生的噪声项;2πΔfNT为残留载波频偏Δf引入的残留载波相位偏差;ΔψNd(t，α)为N符号间隔差分后的差分相位可表示为

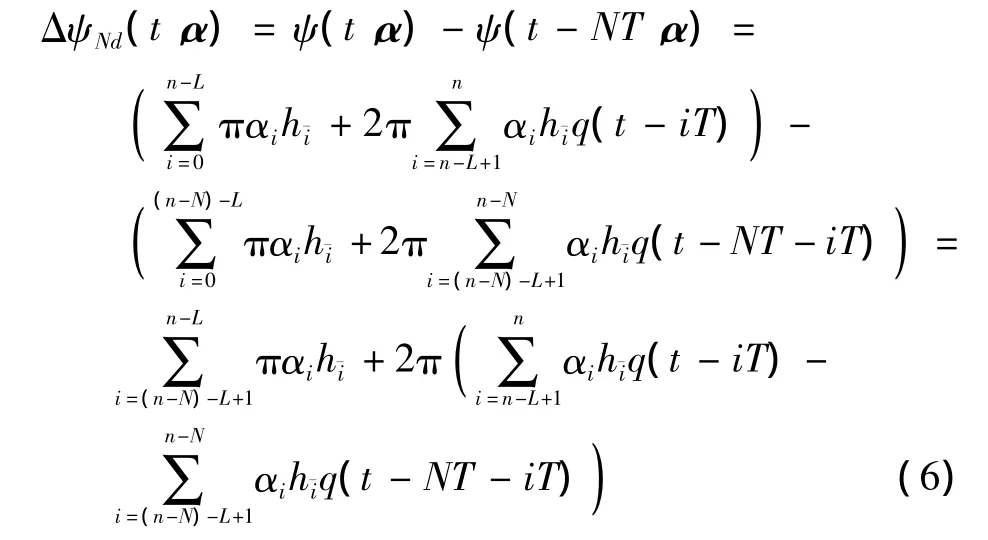
则在nT时刻，经过N符号间隔差分后的Multi-h CPM信号的网格状态σNdn可表示为

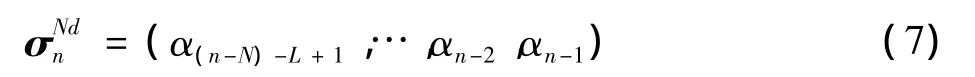
且共有ML+N－1个网格状态项。

由于r(t)是恒包络信号，那么差分信号rNd(t)仍然是恒包络信号，根据非相干最大似然序列检测理论，最大化对数似然函数等价于最大化，则Multi-h CPM信号的N符号差分检测的分支度量可以表示为

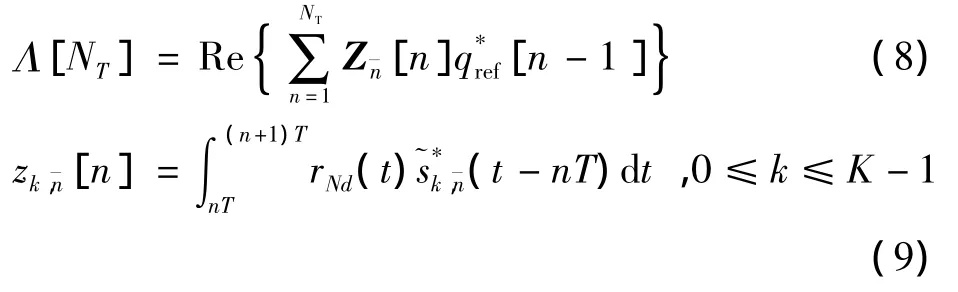
式中:NT为序列检测的符号长度;qref［n－1］为参考相位，表示对式(5)中的残留载波相位偏差2πΔfNT的估计;(t)表示状态网格中的第k个支路的参考差分信号，在N符号差分检测的状态网格中共有K=ML+N个支路;矢量表示匹配滤波器的输出。

则分支度量的增量可表示为

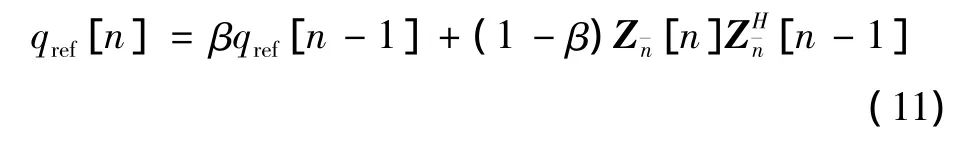
式中:β为遗忘因子，且0≤β＜1。

2.3 减少网格状态数量

从式(7)可知，部分响应长度L、进制数M、差分的符号间隔数N决定了文中算法的网格状态数量，以M=4，L=3，h={4/16，5/16}升余弦成形的 ARTM Tier2信号为例，1符号差分检测时共有64个状态，2符号差分时共有256个状态，与其相干最佳解调的512状态相比，1符号差分检测和2符号差分检测的状态数量虽然有一定程度的减少，但是其实现复杂度仍然是相当大的。为此运用文献［10］中的PSP处理技术利用网格上每个网格状态对应的幸存路径上的假设判决码元估计出维特比算法中影响分支度量计算的未知状态项，从而减少网格状态的数量。如可将网格状态中的(α(n－N)－L+1)作为未知状态，用每一条幸存路径的判决结果对该幸存路径上的α(n－N)－L+1值进行估计，再将估计所得的作为已知量代入分支度量计算。

以ARTM Tier2信号的1符号差分检测为例，将状态项(αn－3)作为未知参数后，则网格状态中只剩下16个状态项，即

式中:是通过幸存路径上的假设判决码元判决反馈得到。同理，也可把 (αn－3，αn－2)同时作为未知状态项，则网格状态中只存在4个状态的相关状态项αn－1，即

图1给出了Multi-h CPM信号的减少状态多符号差分非相干检测器的结构框图。

图1 Multi-h CPM信号的减少状态多符号差分非相干检测器结构框图

3 调制指数的估计与同步

在合作通信模式下，虽然接收信号的调制指数h¯n被限定属于一个有限且已知调制指数集合Π，但是Multi-h CPM信号的若干调制指数周期循环变化，因此Multi-h CPM信号检测器需准确地判断出当前接收信号相邻码元符号之间调制指数周期循环变化的顺序，即调制指数的估计与同步。以ARTM Tier2信号为例，假设一个任意固定的kT时刻作为某次ARTM Tier2信号接收的起始时刻，那么在nT时刻，接收的码元符号 {αk，…，αn－1，αn}所对应的调制指数序列H¯n有2种可能，即={…，4/16，5/16}或={…，5/16，4/16}，由于 ARTM Tier2信号的调制指数以Nh=2周期循环变化，若nT时刻的调制指数序列H¯n已知，那么该次完整接收的调制指数序列便可知。为了便于分析，可分别记这2种可能的调制指数序列为H(0)={4/16，5/16}或H(1)={5/16，4/16}。

但是Multi-h CPM信号的调制指数的同步，其实现复杂度是相当巨大的［11-12］。根据最大似然序列检测理论，当接收信号与本地恢复信号完全相参时，其网格中的分支度量才会达到最大值，那么接收端可以遍历当前接收信号所有可能的调制指数序列，然后判定最大分支度量值所对应的调制指数序列为其实际接收信号调制指数序列的估计值。设t=N0为某次Multi-h CPM信号的N符号差分检测的起始时刻且该差分信号的实际调制指数序列为H，那么在nT时刻，接收端就有Nh种可能的调制指数序列，即

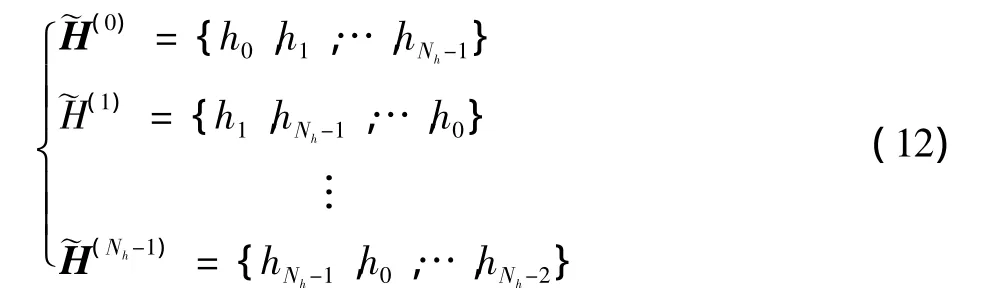
设检测器分别按照Nh种可能的调制指数序列，，…，生成所对应的参考N符号差分信号和网格状态转移图对接收信号进行匹配滤波和分支度量计算，经过Ne个符号间隔的路径度量计算后，检测器搜索Nh种可能的调制指数序列所对应的分支度量值，只有与实际接收信号的调制指数序列H一致的所对应的分支度量值达到最大值，该值即为实际接收信号调制指数序列H的估计值。为了便于分析，设取自一个有限的离散集合，则通过分支度量估计调制指数序列H的表达式为

值得注意的是，观察符号间隔长度Ne的值决定了调制指数序列估计值的精度。但随着Ne的增加，其计算量也呈指数形式增加，为了达到计算量和估计精度的折中，Ne的取值应小于2 000。

4 性能仿真与分析

为了衡量所提出算法的性能，利用MATLAB软件对文中算法进行仿真，Multi－h CPM信号体制为ARTM Tier2信号，符号速率为5 Mbaud，过采样倍数为4，维特比译码的回溯深度为16个符号，信道为加性高斯白噪声信道。

图2和表1分别给出了接收端已完成调制指数同步时，ARTM Tier2信号的1符号差分检测(1DN－全状态)、2符号差分检测(2DN－全状态)以及其减少状态差分检测(DN－PSP)的误比特率性能和实现复杂度比较。从图表中可以看出，当误比特率为10－4时，与相干检测相比，1DN－全状态差分检测和2DN－全状态差分检测别损失约5.8 dB和3.8 dB，可见随着差分间隔数的增加，其检测性能随之增加且实现复杂度也呈指数形式增加。

图2 ARTM Tier2信号的多符号差分检测性能

表1 ARTM Tier2信号的多符号差分检测的复杂度比较

与全状态差分检测相比，由于引入PSP处理减少其网格状态数量，只存在一个未知状态项的1DN－PSP－16状态差分检测与2DN－PSP－64状态差分检测的网格状态分别从原来的64和256减少到16和64，且其检测性能分别仅损失约0.2 dB和0.17 dB;同时存在两个未知状态项的1DN－PSP－4状态差分检测与2DN－PSP－16状态差分检测的网格状态分别减少到4和16，且其检测性能分别损失约1.2 dB和0.6 dB，这说明PSP处理能有效地减少其网格状态数量且性能损失较小，同时随着未知状态项数量的增加，造成其欧氏距离减少，从而使得其检测性能随之进一步恶化。虽然减少状态差分检测的性能略差于全状态差分检测，但减少状态差分检测的网格状态数量却大幅度降低，对于其中的未知状态项的估计，仅需要利用当前幸存路径的判决结果便能实现对其估计，所付出的代价是很小的。总体而言，与相干检测相比，多符号差分检测及其减少状态差分检测的性能有一定程度的恶化，但是其不需要恢复信号的载波相位，这对载波相位恢复相对困难的ARTM Tier2信号是较为有利的。

图3接收端已完成调制指数同步且归一化残留载波频偏ΔfT=0.01时，ARTM Tier2信号的1符号差分检测、2符号差分检测以及其减少网格状态差分检测的误比特率性能。从图3中可以看出，当误比特率为10－4时，与其无载波残留频偏时(ΔfT=0)的差分检测相比，1DN－全状态差分检测和2DN－全状态差分检测分别损失约为0.08 dB和0.7 dB，1DN－PSP－16状态差分检测和2DNPSP－64状态差分检测分别损失约为0.2 dB和1.6 dB。可见随着差分间隔数的增加，其抗残留载波频偏的性能随之下降且减少状态差分检测的性能损失要比其相应的全状态差分检测的性能损失要大。

图3 存在残留载波频偏时，ARTM Tier2信号的多符号差分检测性能

图4给出基于多符号差分检测的ARTM Tier2信号的调制指数估计的性能。从图中可以看出，在中高信噪比阶段2符号差分检测的估计性能明显优于1符号差分检测的估计性能。总体来看，对于不同状态数量的差分检测算法其调制指数估计性能均有较好的仿真结果。在比特信噪比为12 dB时，其估计正确概率均能达到1，在实际应用中其性能也是较为优异且能够满足其实际应用。

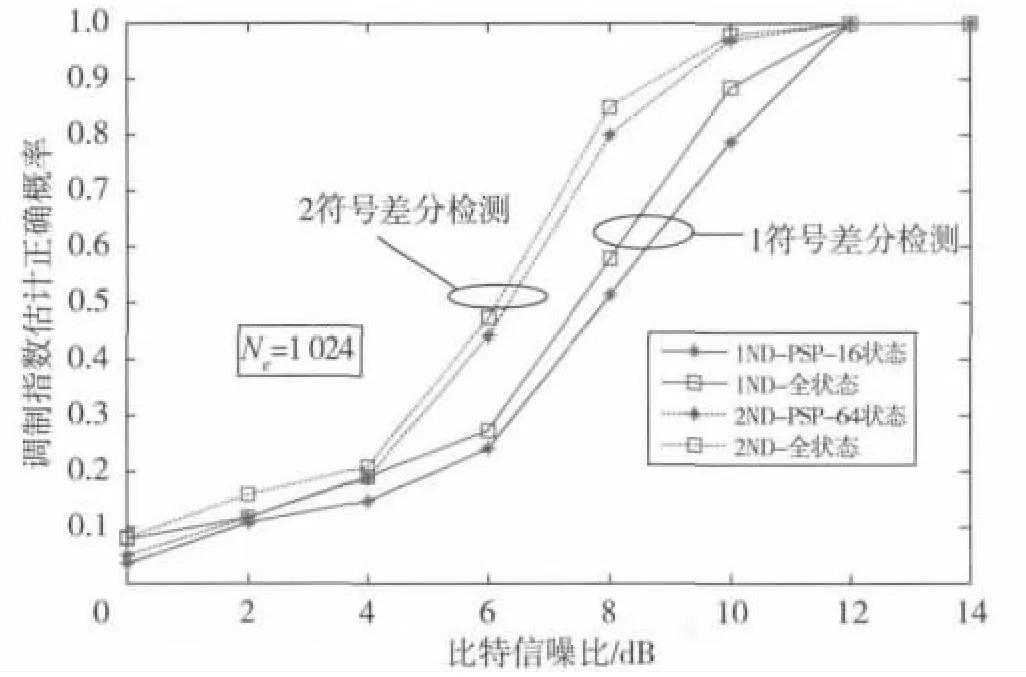
图4 ARTM Tier2信号的调制指数估计性能

5 小结

文中提出了一种适用于Multi－h CPM信号的减少状态多符号差分非相干序列检测算法。在利用逐幸存处理技术减少网格状态的基础上，该算法采用多符号差分信息和参考相位信号实现了具有残留载波频偏校正的差分非相干序列检测，使接收端能以较小的性能损失获得复杂度的降低。同时文中算法利用维特比译码的分支度量实现其调制指数的估计与同步，而不需要额外的调制指数同步模块，从而简化了Multi－h CPM接收机的结构，有利于系统的实现。

:

［1］刘春江，吴志跃，郭沛宇，等.数字卫星广播中CPM与OPSK调制性能仿真与分析［J］.电视技术，2009，33(S1):4－5.

［2］ZHOU H，BRUCK J.Efficient generation of random bits from finite state Markov chains［J］.IEEE Trans.Information Theory，2012，58(4):2490－2506.

［3］PIMENTEL C，VALDEMAR C.On the power spectral density of constrained sequences［J］.IEEE Trans.Communications，2007，55(3):409－416.

［4］SALEEM S，STUBER G L.Trellis termination of Multi－h CPM and Diophantine frobenius problem［J］.IEEE Trans.Communications，2011，59(8):2196－2205.

［5］周家喜，李辉，戴旭初，等.连续相位调制的非相干符号网格解调算法［J］.电子与信息学报，2009，3(9):2137－2142.

［6］VALENTI M.C，CHENG S，TORRIERI D.Iterative multisymbol noncoherent reception of coded CPFSK［J］.IEEE Trans.Communications，2010，58(7):2046－2054.

［7］杨友福，刘建伟，张其善，等.基于多符号分组的CPM软输出非相干检测算法［J］.通信学报，2012，33(8):114－117.

［8］孙锦华，吴小钧.CPM信号的多分支分数多比特差分检测［J］.西安电子科技大学学报:自然科学版，2010，37(3):423－428.

［9］DEMIR A，MEHROTR A，ROYCHOWDHURY J.Phase noise in osillators:a uniftying theory and numerical methods for characterization［J］.IEEE Trans.Circuits Systems，2000，47(5):655－674.

［10］RAHELI R，POLYDOROS A，TZOU C K.Per－survivor processing:a general approach to MLSE in uncertain enviroments［J］.IEEE Trans.Communications，1995，43(2):354－364.

［11］BIANCHI P，LOUBATON P.Non－data aided estimation of the modulation index of continuous phase modulations［J］.IEEE Trans.Signal Processing，2004，52(10):2847－2861.

［12］NAPOLITANO A，SPOONER C.Cyclic spectral analysis of continuousphase modulated signals［J］.IEEE Trans.Signal Processing，2001，49(1):30－44.