BP神经网络在油液污染与磨损预测中的应用

田勇，廉书林，，陈闽杰

(1.河南工业大学机电工程学院，河南郑州450007;2.广州机械科学研究院设备润滑与磨损状态监测中心，广东广州510701)

现代化工业技术的不断发展，机械设备日趋大型化、智能化、自动化、复杂化和连续化，一旦发生故障，将会给生产、甚至人们的生命财产造成不可挽回的损失。因此，利用技术手段对机械设备的状态监测和故障诊断，具有重要的现实意义［1－2］。如果能够利用有效的数学方法，建立油液污染与磨损之间的关系，那么将能够为设备的下一步的维护提供可靠的依据，也将会加快“定期维护”到“视情维护”转变的步伐，同时，也将为企业节约大量的人力、物力资源，保护生态环境，实现可持续发展。

作者在大量检测数据的基础上，利用人工神经网络技术，采用共轭梯度法与Levenberg-Marquardt法建立油液污染与机械磨损模型，获取污染与磨损之间的规则，并判别该方法的可行性。通过对比传统神经网络与改进型神经网络所得到的试验结果，说明改进的神经网络在油液污染与磨损的预测方面比传统的神经网络具有更好的泛化能力，旨在为油液污染与机械磨损的判别提供一种新的思路［3］。

1 BP神经网络算法改进

Back Propagation Network，简称为BP神经网络，是基于误差反向传播算法的多层前馈网络，它具有模拟人类大脑神经处理信息的特殊性，且拥有强大的学习能力和大规模计算功能，能够解决很多传统方法难以解决的问题。由于BP神经网络具有自学习、非线性映射、自适应能力等优点，同时能够较好地实现各指标与评价结果之间非线性关系的映射，具有很好地函数逼近能力，所以该网络也是目前应用最广泛和最成功的一种神经网络［4－6］。

1.1 共轭梯度法

针对传统的BP神经网络算法收敛速度慢的特点，提出了共轭梯度法。这种方法的第一步是沿着负梯度方向进行搜索，然后沿着当前搜索的共轭方向进行搜索，可以迅速的达到最优解。以X(k)代表网络所有权值和阈值所组成的向量，η(k)表示在S(X(k))的方向上，使f(X(k+1))达到极小的步长。具体描述如下:

第一次迭代的搜索方向确定为负方向，如式(1)所示:

其后迭代方向为:

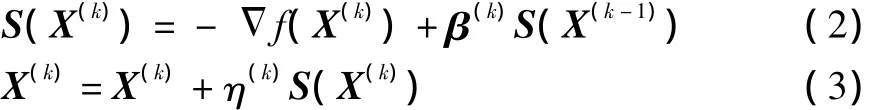
在实际运用过程中根据β(k)的不同所取的形式不同，常见的一般有两种形式:

文中采用式 (4)。但是，在实际应用中还会不可避免地出现陷入局部最小值的局面。因此，考虑采用附加动量法对权值进行修正，即加入动量因子mc，这样使网络的训练自动地避免陷入局部最小，具体的方法是将权值公式调整为

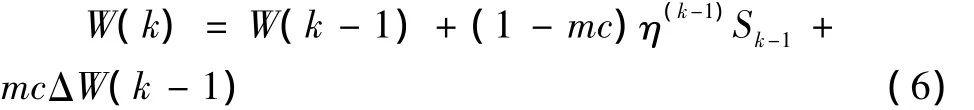
1.2 Levenberg-Marquardt法

鉴于梯度下降法在开始几步下降速度快，但随着接近最佳目标值，梯度会逐渐趋近于0，使得目标函数的下降缓慢;而高斯－牛顿法可以在接近目标值的情况下产生一个最佳的搜索方向，提出Levenberg-Marquardt法 (以下简称L-M法)。L-M法是梯度下降法和高斯－牛顿法的结合。由于L-M算法利用了近似的二阶导数信息，通过自适应调整阻尼因子来达到本身的收敛特性，所以这种方法具有更高的迭代收敛速度，既有梯度法的全局特性，又有高斯－牛顿法的局部收敛性。L-M法的搜索方向为:

如果令 η(k)=1，则 X(k+1)=X(k)+S(X(k))。在开始计算时如果取η是一个相对来说很大的数，则相当于梯度下降法以很小的步长开始计算，每迭代成功一次η的值就会减小一点，随着最优解的接近，η就会减小到0，此时S(X(k))将会从负梯度的方向转向牛顿法的方向。由于BP神经网络在训练目标函数时常常具有平方和的形式，因此，式 (7)用到的Hessian矩阵可以通过包含网络误差对权值和阈值一阶导数的Jacobian矩阵进行近似计算，即H=JTJ。

2 实例应用

2.1 样本处理

数据来源于广州机械科学研究院设备状态检测研究所2011-2012年度对华润水泥控股有限公司部分机组 (编号为1线1#、2线2#的水泥磨主减速机和1线、2线的回转窑主减速机)齿轮箱油液的检测结果。根据油液检测的基本理论知识，以Al、Cu、Fe、Sn、大、小磨粒读数DL、DS作为齿轮箱的磨损指标，同时也作为BP神经网络的输入;将油液的污染程度分为正常、注意、警告，作为输出。由于网络的各个输入具有不同的物理意义和不同量纲和数量级，为了使各个参量能够得到平等使用，避免因函数变换出现的误差，在数据写入程序前首先利用Matlab工具箱中的Premnmx()函数把数据归一到 ［－1，1］之间［6］。表1是未经归一化的部分数据。对数据归一化后，考虑到样本中可能存在冗余的数据最终会影响测试结果，因此提出一种离散度―新陈代谢法对数据进行处理。即计算出归一化后每一组数据的离散度，去掉离散度最大的前3组数据，然后加入新的数据，并与前者进行对比。

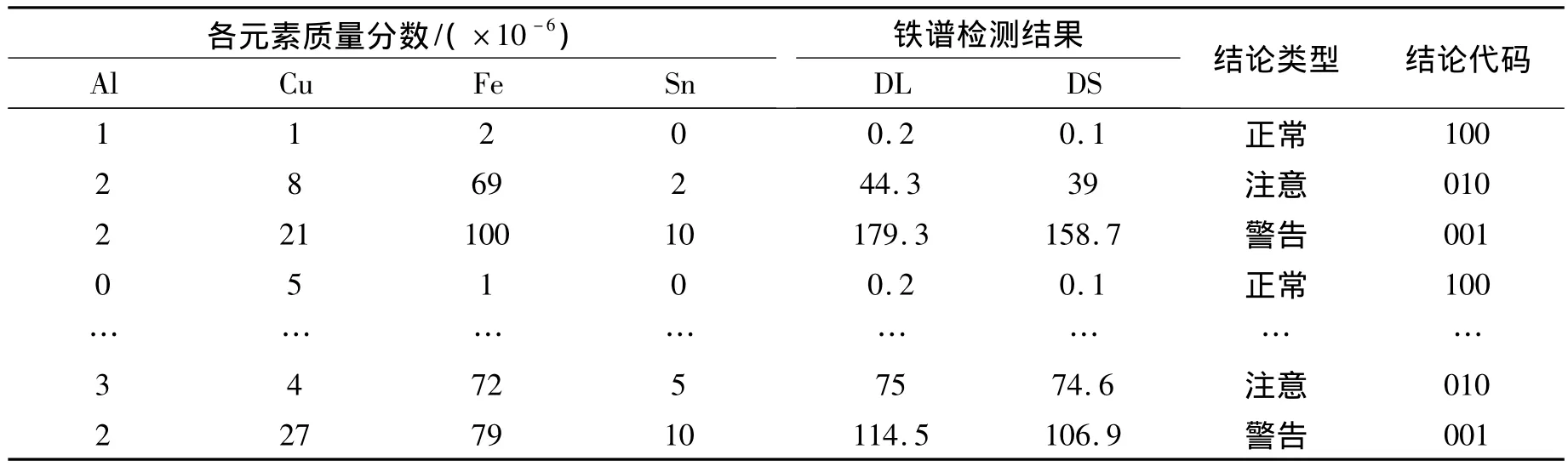
表1 部分样本数据

2.2 网络构建

由于一个三层BP神经网络能够完成任意的n维到m维的映射，文中所设计的网络采用单隐含层的BP网络进行训练和预测，选取满足条件的60组数据进行网路的训练，6组数据对训练后网路的置信度进行测评。由于输入样本为六维的输入向量，因此输入层一共含有6个神经元;对于网络输出为了便于统计和分析，将正常定义为100，注意定义为010，警告定义为001，这样输出变为3个单元。对于各隐层神经元个数的选取，目前还没有统一的方法，本文根据逐增步长的方法最终确定隐层神经元个数，经过反复的训练，网络的结构最终确定为6×12×3;隐含层和中间层的的传递函数分别采用Tansig和Logsig，输出层函数根据方法的不同而选取不同的函数，最大训练次数为1 000，期望误差设为0.01。

图1 快速下降法训练误差曲线

图2 共轭梯度法训练误差曲线

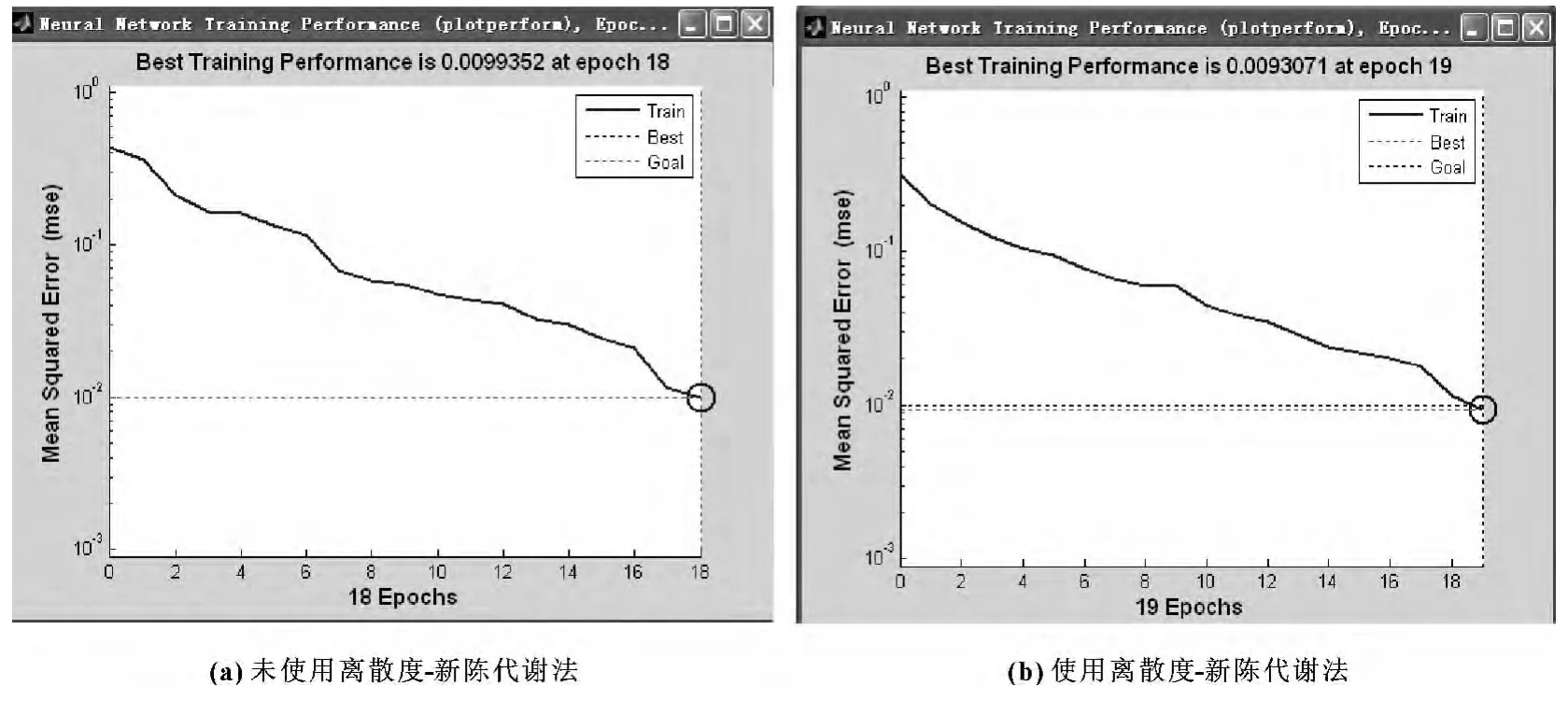
图3 L-M法训练误差曲线

表2 预测结果

2.3 结果与分析

对表1中的数据分别用传统神经网络法、共轭梯度法与L-M法三种神经网络进行对比分析。图1、图2、图3分别是3种方法的训练误差曲线，图 (a)表示没有使用离散度―新陈代谢法进行数据处理的误差曲线图，图 (b)表示使用离散度―新陈代谢法进行数据处理的误差曲线图。表2是3种方法预测的结果。由图1、2、3可知，共轭梯度法和L-M法与传统的BP网络法相比具有更小的误差，并且在训练速度上有了很大提高。从图形曲线的走势可以看到，改进后的神经网络误差曲线更加平滑，这也体现出了改进后的网络跳出局部极小值的能力有明显的增强。从预测结果来看，经过改进后的神经网络预测结果的精度明显的高于前者，具有更好的泛化能力。

3 结论

(1)分别构建了传统神经网络法、共轭梯度法、L-M法3种方法下的齿轮箱油液污染与磨损关联度模型，从预测结果可以看到，应用BP神经网络对油液污染与磨损之间相关关系的评价是合理可行的。

(2)通过传统BP神经网络算法与改进BP网络算法的对比，改进后的BP神经网络算法在污染与磨损关联的预测上具有更高的精度。

(3)通过3种方法图 (a)与图 (b)以及表2预测结果的对比，可以看到使用离散度－新陈代谢法对数据进行处理后BP神经网络的预测精度和预测速度都有所提高。

【1】崔东文．基于改进BP神经网络模型的云南文山州水资源脆弱性综合评价［J］．长江科学学院院报，2013，30(3):1－7．

【2】张德丰．MATLAB神经网络应用设计［M］．北京:机械工业出版社，2012．

【3】宋海军，陈步英，李洪燕，等．基于BP神经网络的煤矿机械故障诊断专家系统的开发［J］．煤矿机械，2012，33(8):1－7．

【4】OUAZZANE A K，CASTAGNER J L，JANKOWSKI H，et al．Characterization of the Coal Fly ash for the Purpose of Improvement of Industrial on-line Measurement of Unburned Carbon Content［J］．Fuel，2004，83(13):1847 －1853．

【5】兰远东，邓辉舫．一种改进离散度的特征选择方法［J］．计算机系统应用，2012，21(7):215 －218．

【6】谢东，陈国荣，施金良，等．基于BP神经网络数控机床切削能耗的研究［J］．机床与液压，2012，40(1):54－57．

【7】刘维群，李元臣．BP网络中隐含层节点优化的研究［J］．交通与计算机，2005，23(2):83 －86．