分数阶异结构超混沌系统完全同步与反相同步控制*

董俊 张广军 姚宏 王珏 许根

(1．空军工程大学理学院，西安 710051)(2．西安交通大学生命科学与技术学院生物医学工程研究所，西安 710049)(3．空军第一航空学院，信阳 464000)

分数阶异结构超混沌系统完全同步与反相同步控制*

董俊1，3张广军1，2†姚宏1王珏2许根1

(1．空军工程大学理学院，西安 710051)(2．西安交通大学生命科学与技术学院生物医学工程研究所，西安 710049)(3．空军第一航空学院，信阳 464000)

以分数阶Lü混沌系统和分数阶Chen超混沌系统为例，研究了维数不同、分数阶次不相等的异结构的混沌系统和超混沌系统的完全同步和反相同步．首先，基于分数阶系统稳定性理论和非线性动力学理论，构造出相应的非线性控制器，实现了两个维数不同，分数阶次不相等异结构混沌系统与超混沌系统的完全同步和反相同步;其次，基于分数阶稳定性理论，对上述两类同步给出了严格的数学证明;最后，借助于预估－校正算法，利用数值模拟验证了所提方法的有效性．

分数阶， 超混沌系统， 完全同步， 反相同步， 非线性控制器

引言

混沌现象是非线性动力学系统所特有的一种复杂运动形式，是自然界普遍存在的复杂现象．近年来，混沌研究是非线性科学领域的热点问题之一，而混沌同步由于其在工程、信息处理、生命科学等领域的潜在应用价值而得到人们的广泛关注［1－2］．近来，除了最初的完全同步人们又提出了许多种混沌同步，如广义同步、相同步、投影同步等［3－5］，当前又有学者提出反相同步的问题，并将此应用到通信领域［6－7］．

分数阶微积分和整数阶微积分几乎具有同样长的发展历史，人们发现:整数阶微积分是分数阶微积分的特例，整数阶混沌系统都是对实际混沌系统的理想化处理［8］．若将分数阶微分算子引入到超混沌系统中，则分数阶超混沌系统能产生更为复杂的动态行为，具有非常强的随机性和不可预测性．分数阶超混沌系统的同步与反相同步控制由于在保密通信、信号处理和系统控制及其他领域比整数阶混沌系统拥有更突出、更诱人的应用前景，从而促进了分数阶超混沌系统的应用研究以及分数阶微积分理论的发展［9］．

由于实际应用中不同结构混沌系统的广泛存在，对于不同结构混沌系统之间的同步与反相同步的研究已取得了一些研究成果．例如，蔡娜［10］等采用主动控制方法，实现了系统参数已知时不同结构混沌系统之间的同步与反相同步;闵富红［11］等利用线性系统稳定性理论，结合反馈控制，实现四维超混沌系统的同结构及异结构的广义投影同步;文献［12］中研究了分数阶Liu混沌系统和统一混沌系统的动力学行为，利用主动控制方法实现了分数阶Liu系统与分数阶Lorenz系统及分数阶Lü系统的异结构同步，该性质对混沌保密通信具有一定的理论意义．根据目前相关文献报道，在维数相同的情况下，异结构整数阶混沌系统之间的同步与反相同步问题的研究已经比较成熟［13－15］;在维数相同、分数阶次相等的情况下，异结构分数阶混沌系统之间的同步与反相同步的问题在近年来也有了一定的研究［16－17］;然而，在工程实际应用中，系统之间的维数往往是不相同的，不仅仅是低维系统之间的同步，更高维数系统之间的同步更能反映出混沌保密特性．本文认为文献［12］中仅考虑了维数相同的分数阶混沌系统之间的异结构同步，并且在研究混沌系统异结构同步中仅考虑了分数阶次相等的情况;对维数不同，分数阶次不相等的情况下，混沌系统之间的同步的问题没有做进一步研究，同时对分数阶混沌系统之间的反相同步的研究也没有做相关报道．在实际应用中驱动系统和响应系统的结构复杂化更利于安全通信，因此考虑在维数不同、分数阶次不相等的情况下，分数阶超混沌系统的完全同步与反相同步的研究具有重要的实际意义．本文主要是基于以上研究成果，利用分数阶系统稳定性理论和非线性动力学理论，构造出相应的非线性控制器，实现了在维数不同、分数阶次不相等的情况下，三维分数阶混沌系统与四维分数阶超混沌系统之间的完全同步与反相同步．该方法具有适用范围广、以及易于实现等优点，扩展了同步与反相同步的应用范围，并在理论分析的基础上，通过数值仿真验证了该方法的有效性．

1 分数阶微分的定义

在分数阶微积分的研究过程中，对微分和积分的概念提出了许多种定义［18－19］，但是在实际应用中使用较多的是分数阶Riemann－Liouville定义和Caputo 定义，本文采用的是 Caputo 定义［18－19］．

定义 一元函数f(x)的q阶微分Caputo定义为:

其中n是不小于q的最小整数(n－1＜q≤n);a，t分别为积分的下限和上限;q为微分阶数，Γ(n－q)为Gamma函数，f(n)(x)是f(x)的n阶导数．

2 分数阶系统分析、完全同步及反相同步描述

2．1 分数阶混沌系统分析

武相军、王兴元等研究了式(2)所示的分数阶Lü系统:

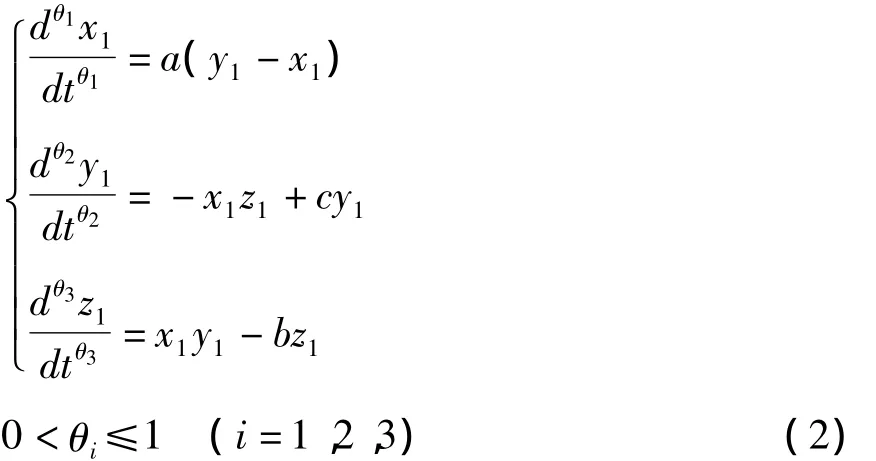
由文献［20］可知，当参数取a=36，b=3，c=20 时，且 θ1+θ2+θ3≥2．5 时，分数阶 Lü 系统(2)处于混沌状态．

我们取参数a=36，b=3，c=20，令 θ1=0．9，θ2=0．94，θ3=0．96 时，采用预估-校正算法［21－22］对分数阶Lü系统(2)进行数值仿真，所得相图如图1所示，与文献［20］中结论相同，可见分数阶Lü系统(2)此时确实处于混沌状态．

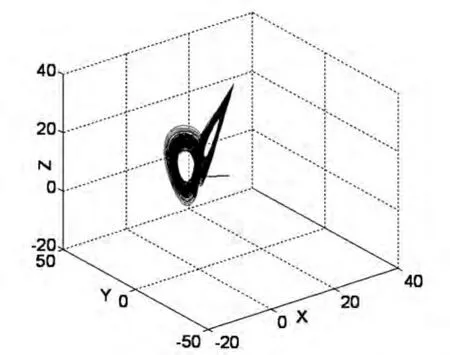
图1 分数阶Lü混沌系统的相图Fig．1 The phase diagram for the fractional－order Lü chaotic system

2．2 分数阶超混沌系统分析

分数阶超混沌Chen系统:

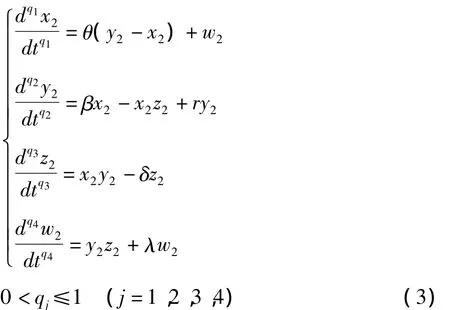
由文献［23］可知，当参数取 θ=35，β=7，r=12，δ=3，λ =0．5 时，0．18 ＜qj＜1(j=1，2，3，4)，分数阶Chen系统(3)是超混沌的．

采用预估-校正算法对分数阶Chen系统(3)数值仿真，当参数取 θ=35，β =7，r=12，δ=3，λ =0．5时，令q1=0．9，q2=0．94，q3=0．96，q4=0．98 时，分数阶超混沌Chen系统相图如图2所示，所得数值解与文献［21］中结论相比较，两者结论相同．

2．3 完全同步与反相同步描述

假设存在如下的驱动系统和响应系统:

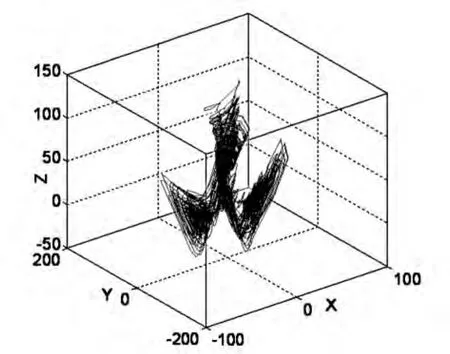
图2 分数阶Chen超混沌系统的相图Fig．2 The phase diagram for the fractional－order Chen hyper－chaotic system

3 分数阶Lü混沌系统与分数阶超混沌Chen系统完全同步控制

本文以分数阶Lü混沌系统(2)为驱动系统，相应的分数阶超混沌Chen系统(3)为受控的响应系统，有:

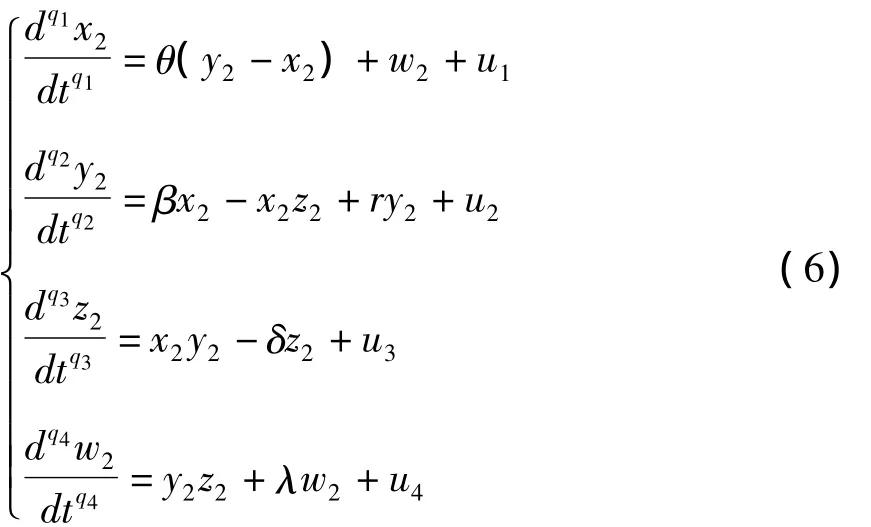
系统(6)中ui(i=1，2，3，4)为非线性控制器．令系统(6)与系统(2)的同步误差为e1=x2－x1，e2=y2－y1，e3=z2－z1，e4=w2－w1，其中w1=0．这里为了方便计算误差系统，将q1= θ1，q2= θ2，q3= θ3，q4= θ4，a=36，b=3，c=20，θ=35，β =7，r=12，δ=3，λ=0．5．可得到如下的误差系统:

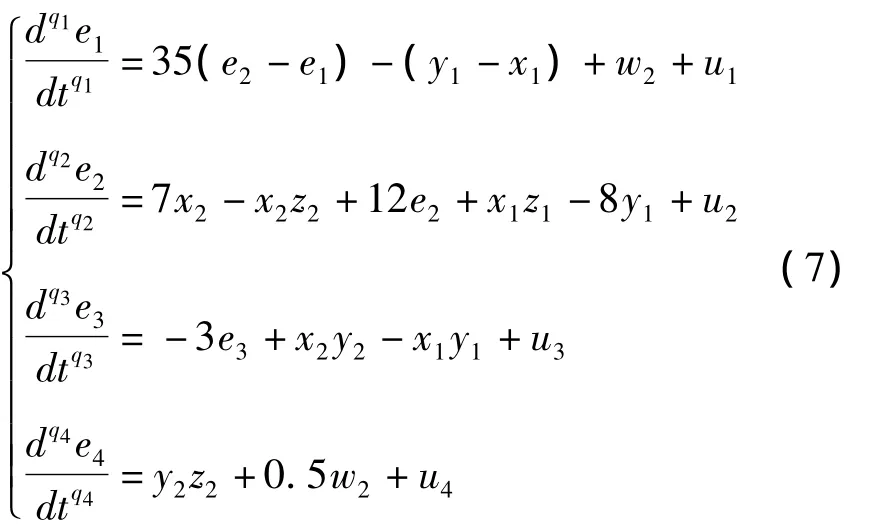
构造相应的非线性控制器，得:

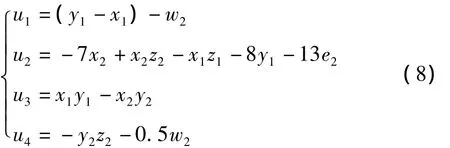
将式(8)代入误差系统(7)，得:

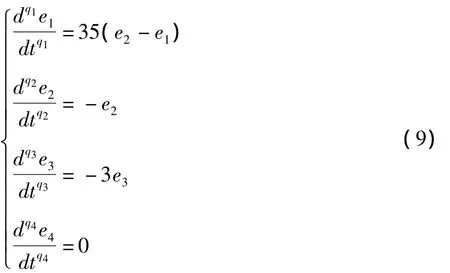
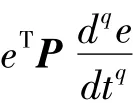
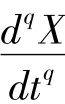
胡建兵［25］等提出了该引理，并对其进行严格的数学证明，指出了该引理既适用于分数阶线性系统也适用于非线性系统的稳定性分析，下面将通过引理来证明定理1．

证明: 由引理推导定理1，如果

成立，分数阶系统(9)稳定．即有

因为矩阵Q为半正定矩阵，故对任意的误差状态变量e:

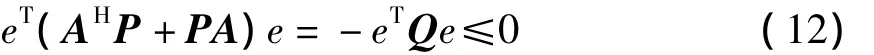
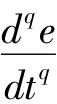
因为矩阵P为实对称正定矩阵，所以有:

从上述证明过程可以看出:由引理推导到定理1，引理成立，故定理1也成立．

根据定理1构造函数:

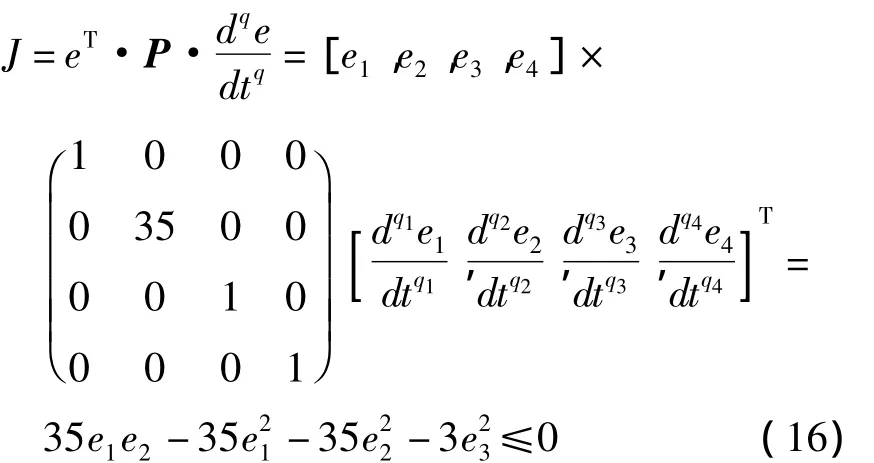
显然式(16)满足定理1，分数阶误差系统(9)的平衡点为(0，0，0，0)，故同步误差e1，e2，e3，e4随着时间渐近趋于零．即在非线性控制器式(8)的作用下，系统(6)与系统(2)在对应的时间序列可以达到完全同步．(证毕)

4 分数阶Lü混沌系统与分数阶超混沌Chen系统反相同步控制

仍然以分数阶Lü混沌系统(2)为驱动系统，相应的分数阶超混沌Chen系统(6)为受控的响应系统，令系统(6)与系统(2)的反相同步误差为e1=x2+x1，e2=y2+y1，e3=z2+z1，e4=w2+w1，其中w1=0．为了方便计算误差系统，将q1=θ1，q2= θ2，q3=θ3，q4=θ4，a=36，b=3，c=20，θ=35，β =7，r=12，δ=3，λ =0．5．可得到如下的误差系统:

构造相应的非线性控制器，得:

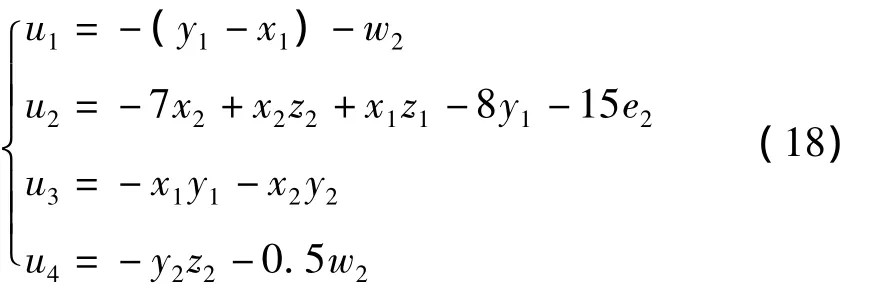
将式(12)代入误差系统(11)，得:

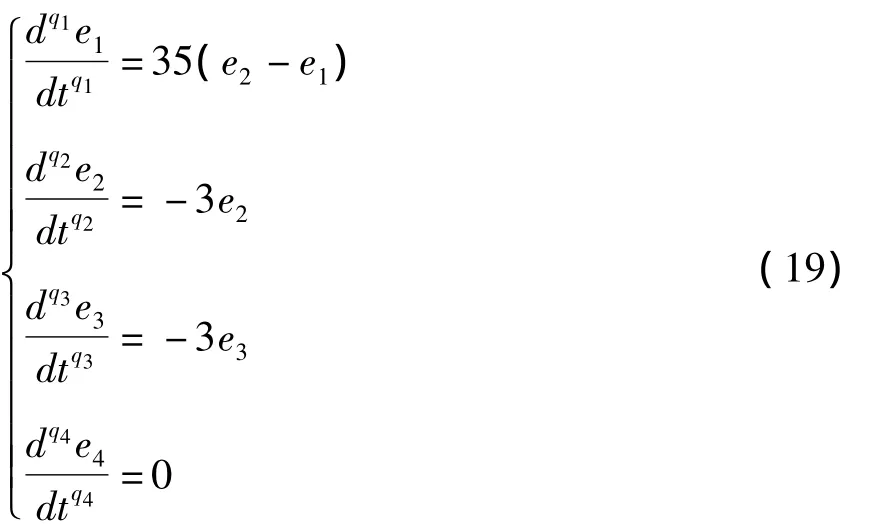
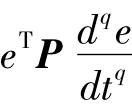
证明: 由引理推导定理2过程与上述引理推导定理1类似，从略．根据定理2构造函数:

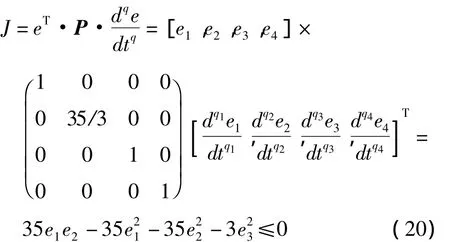
显然式(20)满足定理2，分数阶误差系统(19)的平衡点为(0，0，0，0)，故同步误差e1，e2，e3，e4随着时间渐近趋于零．即在控制器式(18)的作用下，系统(6)与系统(2)在对应的时间序列可以达到反相同步．(证毕)

5 数值仿真分析

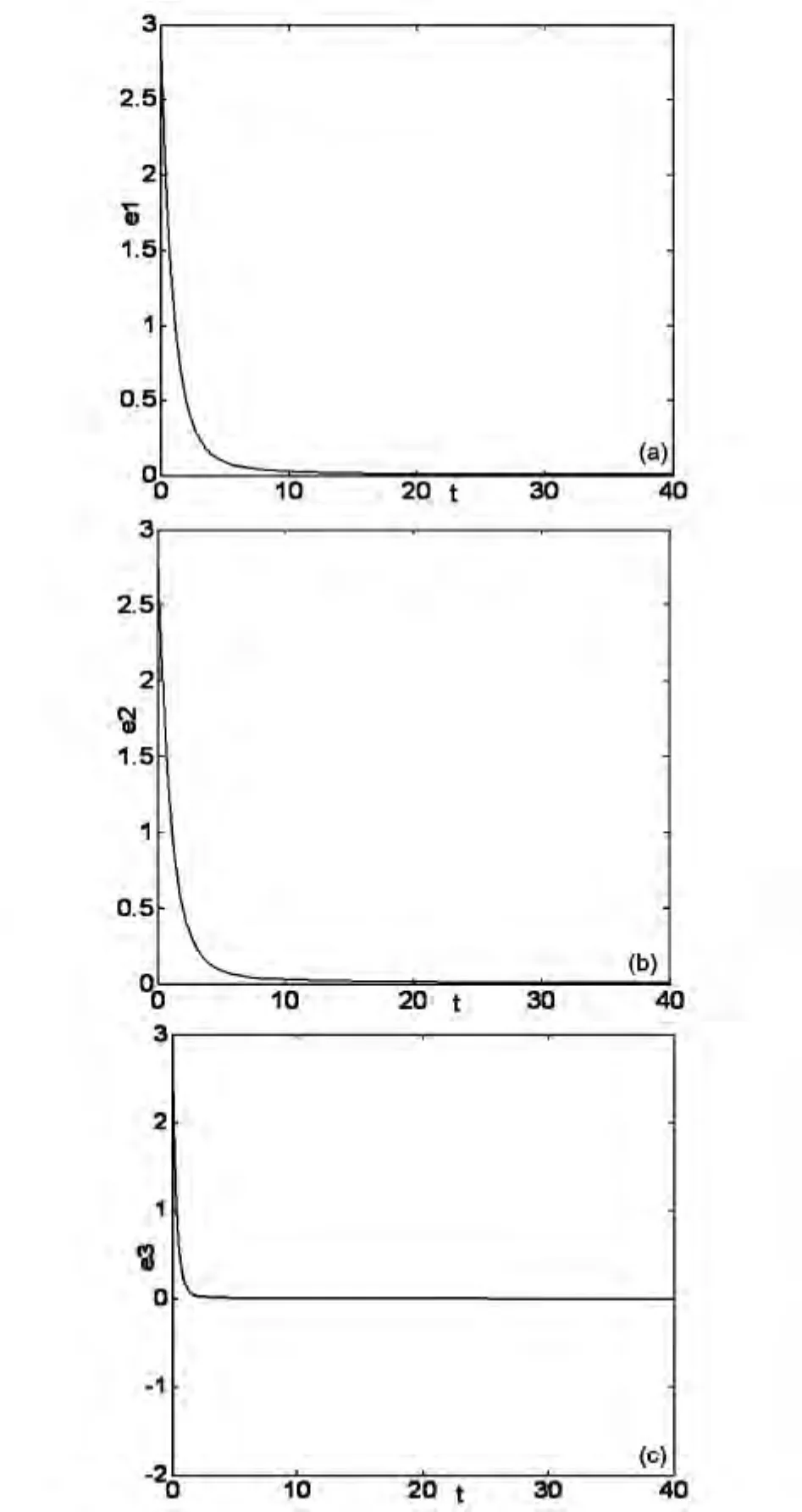
图3 完全同步误差随时间变化的历程图(a)e1(t)～t;(b)e2(t)～t;(c)e3(t)～tFig．3 Time history diagram of the complete synchronization errors:(a)e1(t)～t;(b)e2(t)～t;(c)e3(t)～t

为了验证上述方法的有效性，我们需要解出分数阶的微分方程(2)和(6)，然后计算两个分数阶微分方程解的误差．分数阶微分方程的解法通常有两种途径:解析解法和数值解法．一般来说解析解法有很大的局限性，只能求解一些较简单的方程，在实际应用中广泛采用的是数值解法．分数阶微分方程的数值解法主要有频域解法［26］、时间离散的预估-校正算法［21－22］、Adomian(ADM)分解算法［27］．频域解法在工程中应用较多，但是有较大的局限性，这种算法对系统的定性性质有一定的干扰，文献［28］研究了频域中近似系统与原系统相比较，对存在的缺陷做出了详细的报道．文献［29］对以上三种算法进行了比较:预估-校正算法是一种时间离散算法，与频域算法相比，这种算法精度较高;ADM算法在解分数阶微分方程是一种十分优秀的算法，与预估-校正算法相比，两种算法计算精度接近，运算效率上高于预估-校正算法．本文中在运算效率上没有做过多要求，而对计算精度有一定的要求，因此在解分数阶微分方程均采用预估-校正算法．

图4 反相同步误差随时间变化的历程图:(d)e1(t)～t;(e)e2(t)～t;(f)e3(t)～tFig．4 Time history diagram of the anti－phase synchronization errors:(d)e1(t)～t;(e)e2(t)～t;(f)e3(t)～t

我们采用预估-校正算法对分数阶超混沌Chen系统(6)与分数阶Lü混沌系统(2)的异结构完全同步与反相同步进行了数值仿真．在仿真计算中，我们选取参数a=36，b=3，c=20，θ=35，β =7，r=12，δ=3，λ =0．5 时，令q1= θ1=0．9，q2= θ2=0．94，q3= θ3=0．96，q4=θ4=0．98 时，步长为 0．005，随机选取系统(2)的状态初始值为:x1(0)=1，y1(0)=2，z1(0)=3，系统(6)的状态初始值为:x2(0)=4，y2(0)=5，z2(0)=6，w2(0)=7．得到两个分数阶微分方程的解后，我们根据式(9)计算了两个系统的同步误差，其完全同步误差仿真结果如图3所示．由图3所示，系统状态误差曲线e1(t)，e2(t)，e3(t)很快都趋于零，即两系统达到了完全同步．

对于系统反相同步数值仿真，我们选取相同的参数、计算步长和状态初始值，得到两个分数阶微分方程的解后，我们根据式(19)计算了两个系统的反相同步误差，计算结果如图4所示．由图4可以看出，系统状态误差曲线 很快都趋于零，即系统达到了反相同步．

6 结论

本文以分数阶Lü混沌系统和分数阶Chen超混沌系统为例，研究了维数不同、分数阶次不同的异结构分数阶混沌系统的完全同步与反相同步问题．首先，基于分数阶系统稳定性理论和非线性动力学理论，构造出一种相应的非线性控制器，实现了在维数不相等、分数阶次不相等的情况下，三维分数阶混沌系统与四维分数阶超混沌系统之间的完全同步与反相同步．其次，基于分数阶系统稳定性理论和非线性系统性质定理对三维分数阶混沌系统与四维分数阶超混沌系统的完全同步和反相同步进行了数学证明，结果表明完全同步的误差系统和反相同步的误差系统都在原点渐近稳定，实现了完全同步和反相同步．最后，在理论分析的基础上，利用预估－校正算法对三维分数阶混沌系统与四维分数阶超混沌系统的完全同步误差和反相同步误差进行了数值仿真，仿真结果与理论分析的结果一致，证明了该方法的有效性．该方法可以进一步推广到高维分数阶混沌系统与高维分数阶混沌系统之间的同步与反相同步，具有收敛速度快、应用范围广、易于实现等优点，在工程领域研究中具有一定的理论意义和较广的应用价值．

1 王光瑞，于熙龄，陈式刚．混沌的控制、同步与利用．北京:国防工业出版社，2001(Wang G R，Yu X L，Chen S G．Chaotic control、synchronization and utilizing．Beijing:National defence industry press，2001(in Chinese))

2 冯朝文，蔡理，康强，张立森．一种新的三维自治混沌系统．物理学报，2011，60(3):030503～7(Feng C W，Cai L，Kang Q，Zhang L S．A novel three－dimensional autonomous chaotic system．Acta Physica Sinica，2011，60(3):030503～7(in Chinese))

3 董俊，张广军，姚宏等．异结构超混沌系统的完全同步与反相同步控制．空军工程大学学报(自然科学版)，2012，13(05):90 ～94(Dong J，Zhang G J，Yao H，et al．The control of complete synchronization and anti－phase synchronization for hyper－chaotic systems of different structures．Journal of Air Force Engineering University(Natural Science Edition)，2012，13(05):90～94(in Chinese))

4 贾贞，陆君安，邓光明．不确定混沌系统的混合投影同步．数学杂志，2011，31(2):275～283(Jia Z，Lu J A，Deng G M．Hybrid projective synchronization of uncertain chaotic systems．Journal of Mathematics(P R C)，2011，31(2):275～283(in Chinese))

5 郑皓洲，胡进峰，徐威，刘立东，何子述．一类新型超混沌系统的非线性反馈同步研究．电子与信息学报，2011，33(4):844～848(Zheng H Z，H J F，Xu W，Liu L D，He Z S．Study on synchronization of a new class of hyper－chaotic systems using nonlinear feedback control．Journal of Electronics＆Information Technology，2011，33(4):844～848(in Chinese))

6 罗小华，薛飞，何伦．非自治异结构混沌系统同步及其在保密通信中的应用．重庆邮电大学学报(自然科学版)，2011，23(3):323～327(Luo X H，Xue F，He L．Synchronization between two non－autonomous chaotic systems with different configuration and its application in secure communication．Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition)，2011，23(3):323～327(in Chinese))

7 李农，李建芬，刘宇平．不确定混沌系统的反同步与参数辨识．物理学报，2010，59(9):5954～5958(Li N，Li J F，Liu Y P．Anti－synchronization of uncertain chaotic system and parameters identification．Acta Physica Sinica，2010，59(9):5954～5958(in Chinese))

8 刘崇新．一个超混沌系统及其分数阶电路仿真实验．物理学报，2007，56(12):6865～6873(Liu C X．A hyperchaotic system and its fractional order circuit simulation．Acta Physica Sinica，2007，56(12):6865 ～6873(in Chinese))

9 刘丁，闫晓妹．基于滑模控制实现分数阶混沌系统的投影同步．物理学报，2009，58(6):3747～3752(Liu D，Yan X M．Projective synchronization of fractional order chaotic systems based on sliding mode control．Acta Physica Sinica，2009，58(6):3747～3752(in Chinese))

10 蔡娜，井元伟，张嗣瀛．不同结构混沌系统的自适应同步和反同步．物理学报，2009，58(2):0802～0813(Cai N，Jing Y W，Zhang S M．Adaptive synchronization and anti－synchronization of two different chaotic systems．Acta Physica Sinica，2009，58(2):0802 ～0813(in Chinese))

11 闵富红，王执铨．新型超混沌系统同结构与异结构广义同步．电子与信息学报，2008，30(12):3031～3034(Min F H，Wang Z Q．Generalized synchronization for two same or different new hyper－chaotic systems．Journal of Electronics＆Information Technology，2008，30(12):3031～3034(in Chinese))

12 张成芬，高金峰，徐磊．分数阶Liu系统与分数阶统一系统中的混沌现象及二者的异结构同步．物理学报，2007，56(9):5124～5130(Zhang C F，Gao J F，Xu L．chaos in fractional－order Liu system and fractional－order unified system and the synchronization between them．Acta Physica Sinica，2007，56(9):5124 ～ 5130(in Chinese))

13 李华青，廖晓峰，黄宏宇．基于神经网络和滑模控制的不确定混沌系统同步．物理学报，2011，60(2):020512～5(Li H Q，Liao X F，Huang H Y．Synchronization of uncertain chaotic systems based on neural network and sliding mode control．Acta Physica Sinica，2011，60(2):020512～5(in Chinese))

14 王兴元，王明军．三种方法实现超混沌Chen系统的反同步．物理学报，2007，56(12):6843～6850(Wang X Y，Wang M J．Three methods of anti－synchronization of hyperchaotic Chen system．Acta Physica Sinica，2007，56(12):6843～6850(in Chinese))

15 吕翎，夏晓岚．非线性耦合时空混沌系统的反同步研究．物理学报，2009，58(2):0814～0818(Lü L，Xia X L．Anti－synchronization of nonlinear－coupled spatiotemporal chaotic systems．Acta Physica Sinica，2009，58(2):0814～0818(in Chinese))

16 曹鹤飞，张若洵．基于滑模控制的分数阶混沌系统的自适应同步．物理学报，2011，60(5):050510～5(Cao H F，Zhang R X．Adaptive synchronization of fractional－order chaotic system via sliding mode control．Acta Physica Sinica，2011，60(5):050510～5(in Chinese))

17 闵富红，王执铨．分数阶混沌系统同结构与异结构广义同步．控制与决策，2008，23(9):1025～1029(Min F H，Wang Z Q．Generalized synchronization for fractionalorder chaotic systems with same or different structure．Control and Decision，2008，23(9):1025 ～ 1029(in Chinese))

18 Podlubny I．Fractional differential equations．New York:Academic Press，1999

19 邓伟华．分数阶微分方程的理论分析和数值计算［博士学位论文］．上海:上海大学，2007(Deng W H．Theoretical analysis and numerical computation for fractional differential equations［PhD Thesis］．Shanghai:Shanghai University，2007(in Chinese))

20 武相军，王兴元．分数阶Lü系统中的混沌及其控制．计算机科学，2007，34(12):204～210(Wu X J，Wang X Y．Chaos in the fractional order Lü system and its control．Journal of Computer Science，2007，34(12):204 ～210(in Chinese))

21 Diethelm K，Ford N J，Freed A D．A predictor－crrector approach for the numerical solution of Fractional differential equations．Nonlinear Dynamics，2002，29:3 ～22

22 Li C P，Peng G J．Chaos in Chen＇s system with a fractional order．Chaos Solitons＆Fractals，2004，22(2):443～450

23 刘福才，李俊义，臧秀凤．基于自适应主动及滑模控制的分数阶超混沌系统异结构反同步．物理学报，2011，60(3):030504～10(Liu F C，Li J Y，Zang X F．Anti－synchronization of different hyperchaotic systems based on adaptive active control and fractional sliding mode control．Acta Physica Sinica，2011，60(3):030504 ～10(in Chinese))

24 胡建兵，韩焱，赵灵冬．基于Lyapunov方程的分数阶混沌系统同步．物理学报，2008，57(12):7522～7526(Hu J B，Han Y，Zhao L D．Synchronizing fractional chaotic systems based on Lyapunov equation．Acta Physica Sinica，2008，57(12):7522 ～7526(in Chinese))

25 胡建兵，韩焱，赵灵冬．一种新的分数阶系统稳定理论及在back－stepping方法同步分数阶混沌系统中的应用．物理学报，2009，58(04):2235～2239(Hu J B，Han Y，Zhao L D．A novel stablility theorem fractional systems and its applying in synchronizing fractional chaotic system based on back－stepping approach．Acta Physica Sinica，2009，58(04):2235 ～2239(in Chinese))

26 Charef A，Sun H H，Tsao Y Y el at．Fractal system as represented by singularity function．IEEE Transaction on Automatic Control，1992，37(9):1465 ～1470

27 Adomian，G．A review of the decomposition method and some recent result for nonlinear equation．Mathematical and Computer Modelling，1990，13(7):17～43

28 Tavazoei M S，Haeri M．Unreliability of frequency－domain appoximation in recognising chaos in fractional－order systems．IET Signal Process，2007，1(4):171 ～181

29 刘勇．分数阶模型神经元的动力学特性及其同步［硕士学位论文］．西安:西安交通大学，2010(Liu Y．Dynamiccal characteristics of the fractional－order model neuron and its synchronization［Master Degree Dissertation］．Xi＇an:Xi＇an Jiao tong University，2010(in Chinese)

*The project supported by the National Natural Science Foundation of China(10872156，81071150)，and the Aviation Foundation of China(20111396011)

† Corresponding author E－mail:zhanggj3@126．com

THE CONTROL OF COMPLETE SYNCHRONIZATION AND ANTI-PHASE SYNCHRONIZATION FOR FRACTIONAL-ORDER HYPER-CHAOTIC SYSTEMS OF DIFFERENT STRUCTURES*

Dong Jun1，3Zhang Guangjun1，2†Yao Hong1Wang Jue2Xu Gen1
(1．College of Science，Air Force Engineering University Xi'an710051，China)(2．School of Life Science and technology Xi'an Jiao tong University Xi'an710049，China)(3．The First Aeronautical Institute of Air Force，Xinyang464000，China)

In this paper，the complete synchronization and anti－phase synchronization between the 3－dimensional chaotic system and 4－dimensional hyper－chaotic system with different dimension and fractional order are researched in which the fractional－order Lü chaotic system and the fractional－order Chen hyper－chaotic system are as an example．First，Based on the fractional theory of stability and nonlinear dynamic theory．the nonlinear controller is designed，and by the nonlinear controller the complete synchronization and anti－phase synchronization between different the 3D fractional－order chaotic system and 4D fractional－order hyper－chaotic system with different dimension and fractional order are realized．Second，based on the fractional－order theory of stability the two kind of synchronization are respectively proved strictly in mathematics．Finally，by the Predictor－Corrector scheme numerical simulation，the validity of the method presented in this paper is verified．

fractional－order， hyper－chaotic system， complete synchronization， anti－phase synchronization，nonlinear controller

14 September 2012，

1 April 2013．

10．6052/1672－6553－2013－065

2012－09－14 收到第 1 稿，2013－04－01 收到修改稿．

*国家自然科学基金资助项目(10872156，81071150)，航空基金资助项目(20111396011)

E－mail:zhanggj3@126．com