热致轴向窜动引发的双盘转子扭转振动分析*
潘健智 曹登庆 初世明
(哈尔滨工业大学航天学院137信箱,哈尔滨 150001)
热致轴向窜动引发的双盘转子扭转振动分析*
潘健智 曹登庆†初世明
(哈尔滨工业大学航天学院137信箱,哈尔滨 150001)
以航空发动机整机系统的结构特点及复杂的运行环境为研究背景,运用Lagrange方法建立双盘转子在不平衡激励和轴向窜动影响下的弯扭耦合动力学模型;针对温度非均匀分布以及热膨胀性质引起的转轴轴向窜动,导出转/静盘面接触时环带面摩擦力与摩擦力矩表达式;最后采用4阶Runge-Kutta方法对系统进行数值求解.对系统进行动力学分析的结果表明,对于非对称双盘转子结构,热膨胀所积蓄的温度内力引发的转子轴向窜动将改变转子系统的固有特性,所产生转静件盘面环带面摩擦力与力矩,是造成转轴扭转振动的关键因素之一.
双盘转子, 摩擦振动, 环带面摩擦力矩, 扭转振动, 转子动力学
引言
转子系统是航空发动机等高速旋转机械中的核心部件,在工作状态下往往处于高温、高压、时变温度场以及多场耦合下的复杂环境,同时受到工艺水平的限制转子系统本身也常常存在着诸如不平衡、不对中等问题,致使转子系统产生不同程度的振动.因此转子系统作为发动机研发工作的主体,对其振动特性的分析,及其合理的结构设计以及有效的理论分析在发动机设计与故障排除中都是必不可少的[1-5].
转子碰摩行为是由其他故障所引起的常见次生故障,伴随转静件碰撞-摩擦-形变耦合的复杂动力学过程,则使转子振动异常、转静件磨损、重则会导致转轴扭曲形变、转轴永久热弯曲,甚至破机械破坏失效的重大安全事故.因此对转子系统碰摩振动问题的研究,了解发动机整机振动的动力学特性具有重要的意义.
扭转振动是旋转机械的典型动力学现象之一,也是转子动力学学科研究领域的主要分支之一.对于实际工程问题中的等截面杆件以及等截面细长构件,当它所受到的外力作用在垂直于杆件(细长体构件)轴线平面内的力偶作用时,杆件将发生扭转变形.对于横截面为圆的发动机转子系统的主轴,当发生扭转形变时,转轴的物理性质和横截面几何形状仍旧保持规则性与对称性,在动力学建模与求解上可以适当的进行简化处理并运用材料力学的相关方法予以分析.
迄今为止,国内外学者已对转子系统的扭转振动进行了大量的研究工作.大量实验与理论研究工作表明发动机转子系统的主轴系扭转振动的危害主要表现为以下三个方面:激励扭矩频率接近系统的某阶固有频率时产生共振并破坏轴系;激励扭矩突变时将在转轴局部产生过大扭振冲击应力,损坏轴系;轴系长期承受复杂的不平衡扭矩作用,致使轴系发生扭振疲劳破坏[6-8].文献[9]研究了温度分布对汽轮发电机组转子扭转振动的影响,计算了考虑温度分布后轴系扭振各阶固有频率以及相应的变化情况,分析了这些变化对轴系安全的影响.文献[10]研究了冲击力矩作用下转子的扭转振动.复杂的温度环境将产生结构形变并引发多样的激振力,引起整机不同形式的振动,如弯曲振动、扭转振动、拉压振动、回转涡动以及复杂的耦合振动[11].
本文考虑非均匀温度环境所带来的影响,在文献[12-13]建立热膨胀引发的转/静件挤压面摩擦力模型的基础上,对文献[14]的转子动力学模型进行简化,建立温度非均匀分布环境中双盘转子-支承动力学模型;将Hertz点接触挤压模型改进为环带面接触挤压模型,用以表征轴向窜动引发的环带面接触摩擦过程,建立转/静件挤压引发的面摩擦力与面摩擦矩动力学模型,随后将全周面摩擦力与摩擦扭矩作用引入双盘转子系统的弯扭耦合振动,并分析其产生的影响;采用数值积分法研究了面摩擦作用下双盘转子系统的动力学特征.最后阐明了新模型对于研究分析转子摩擦故障的可行性和针对性.新模型反映了实际的转子结构及其运行特征并且能够较好地适应现有的基础理论与计算方法,减少计算工作量与计算误差;为发动机转子系统故障诊断、维修与结构优化奠定理论基础.
1 盘面摩擦力与摩擦力矩
考虑到发动机转子的结构非对称性以及固有的制造误差,假设两转盘所在的位置将整个转轴分为三个不等长轴段,如图1所示,各轴段长度分别为l1,l2和l3,且l=l1+l2+l3;设转子的左、右轴承处等效支承刚度为kb,质量为mb1与mb2;转子自转转速为Ω;转轴面二次极矩为Ip,剪切模量为G,杨氏模量为E,转轴截面径向惯性主矩为I;转盘i(i=1,2)处的等效质量为mri,偏心距为ei,转盘i的半径为Ri;转动惯量为Ii,封严内半径可近似为Rseal;以左端轴承处集中质量为中心,建立笛卡尔坐标系o-xyz,xy平面平行于转盘平面,oz轴与转轴中线重合.
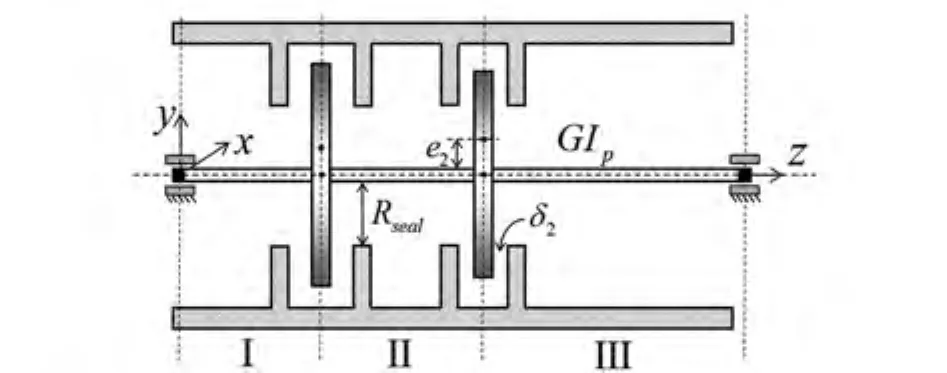
图1 双盘转子-轴承系统的扭转振动模型Fig.1 Model of double-disk rotor-bearing system for torsional vibration
由于温度的非均匀性,使得高速运转的转子系统产生非均匀温度应力,导致转盘产生由高温部分向低温部分的轴向窜动,且窜动位移量与转、静件初始轴向间隙往往为同一个量级,严重情况下会产生转静子盘面挤压.在计算盘面摩擦力与力矩时,不考虑扭转振动、弯曲振动与拉压振动之间的耦合关系.
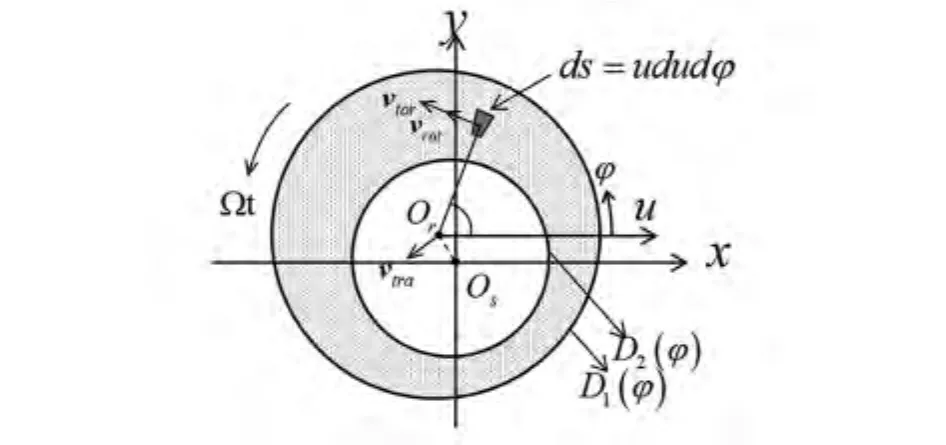
图2 面接触摩擦示意图Fig.2 Schematic diagram of surface contact rubbing
在前述假设下,轴向碰摩近似为两平面的接触挤压,轴向单位面积接触等效刚度ka为一个与材料属性有关的常量,摩擦系数为μ.由文献[12-13]分析可知,受温度环境的影响,转子主轴在热膨胀作用下将产生窜动位移,使得盘面将朝向低温段方向窜动.盘处产生的挤压量δi≥0时,发生轴向环带面接触,其中阴影部分S={(u,φ)|0≤φ≤2π,D2≤u≤D1}为接触面或挤压面.在图2所示的转盘随体极坐标架Oruφ下,D2与D1为对应的内外边界方程,微元ds的速度包含三部分:随转盘质心的刚体平动速度vtran、随转盘自转的速度vroto和盘面扭转速度vtors,微元总速度vds在惯性坐标系o-xyz下的形式为:
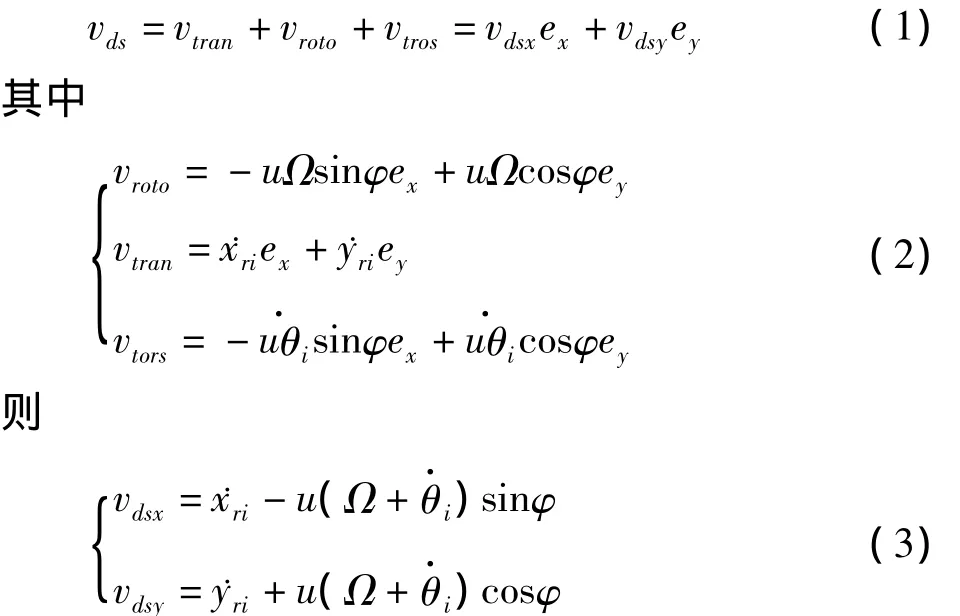
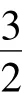
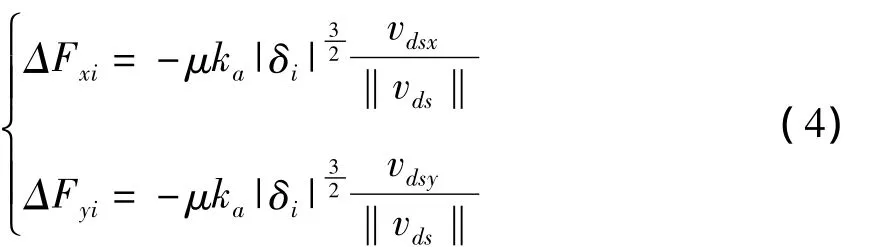
由于盘面接触而附加在盘心上的轴向环带面摩擦力分量为:
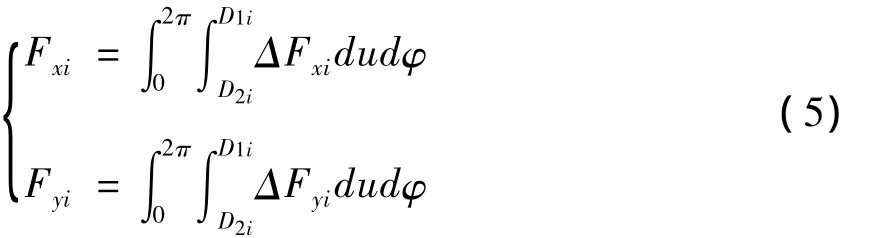
面摩擦产生的作用在转盘i中心上的摩擦扭矩Mzi为:
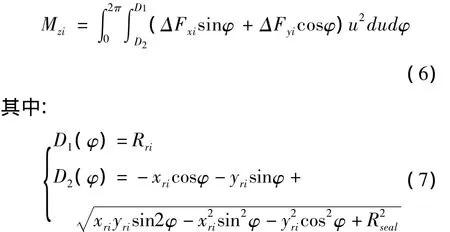
这里vtran=xriex+yriey为发生面接触处的转盘中心速度,是由于转盘的不平衡量在转动时引发的偏心周期激励所产生.
2 双盘转子扭转振动动力学建模
为研究转轴扭转振动,将转盘与轴承处的相对转角变化θ1和θ2取为扭转模型的广义坐标,如图3所示,系统扭转振动的动能:

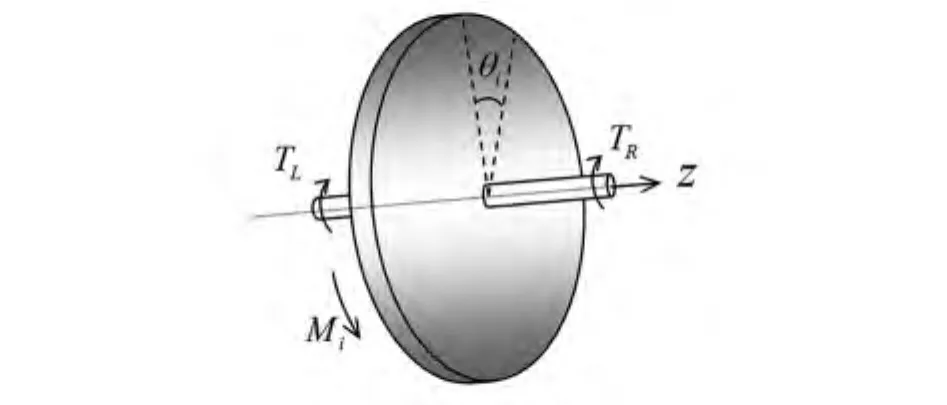
图3 转盘扭转角坐标Fig.3 Torsion angle coordinate of the ith disk
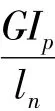
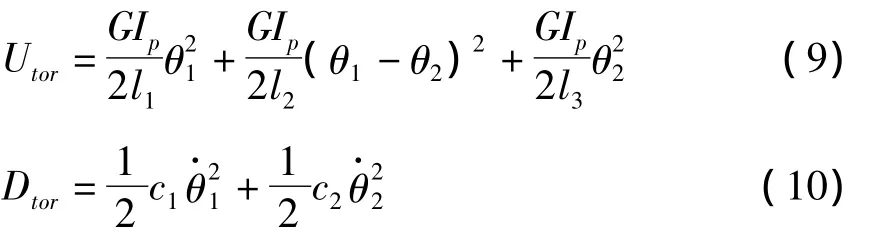
作用在系统双盘处的广义力为:

采用Lagrange法可以整理得到双盘转子系统的扭转振动微分方程为:
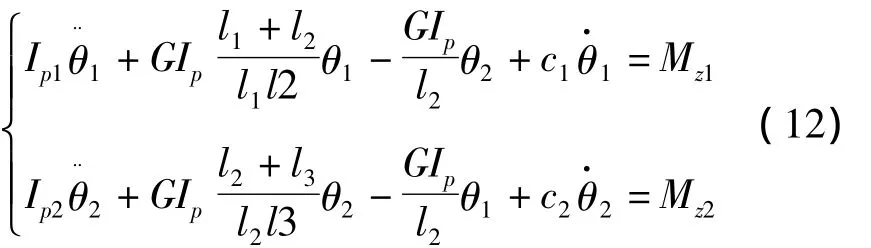
其中Mz1和Mz2为面摩擦引起的周期扭矩激励,形式如方程(6)所表述.
3 双盘转子弯扭耦合振动微分方程
航空发动机在通常的运行情况下,转轴将会发生扭转与弯曲组合变形.本节将建立转子主轴在该组合变形下双盘转子系统的动力学模型,并讨论相关的动力学特性.取(θ1θ2xr1xr2yr1yr2xb1xb2yb1yb2)为广义坐标,采用柔度影响系数法与 D'Alember原理建立系统的运动微分方程.
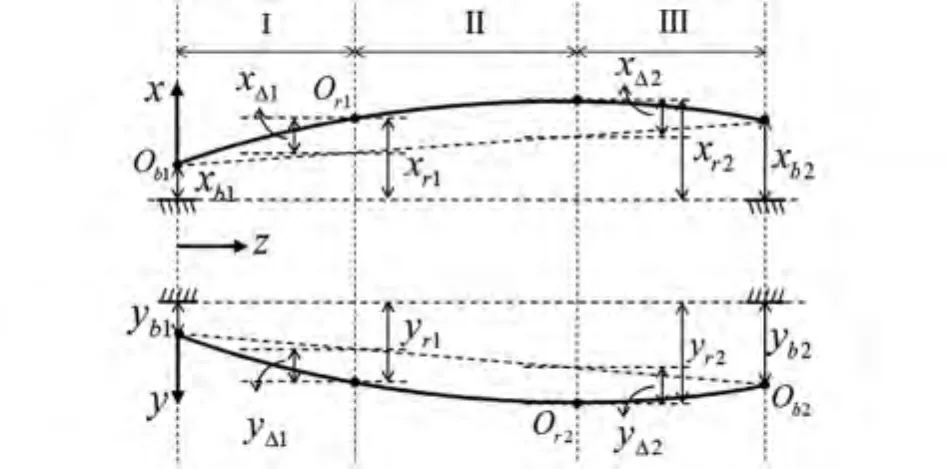
图4 OXZ与OYZ面内转轴弯曲示意图Fig.4 The Shaft bending schematic diagram in OXZ and OYZ
转轴在oxz与oyz面内的弯曲如图4所示:考虑oxz面内的弯曲变形(oyz内的情况类同),设转轴上转盘形心在ox方向上的弯曲柔度矩阵为H=(hij),H-1即为转轴弯曲刚度矩阵.应用弯曲变形理论可计算出H的分量为:
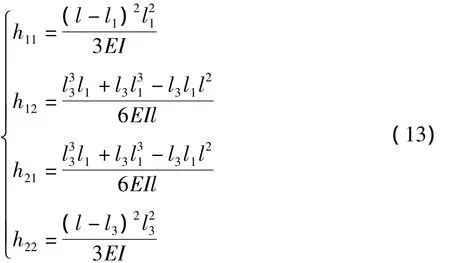
转盘处的运动微分方程为:
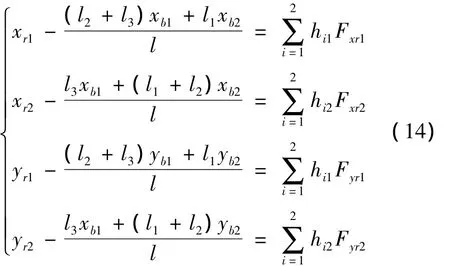
其中:
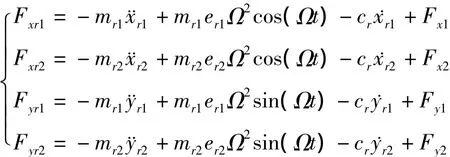
Fx1,Fx2,Fy1,Fy2为转盘所受到的外激励.轴承的平衡关系为:
方程(15)中系统由转轴弯曲所累积的势能总和Ufle为:
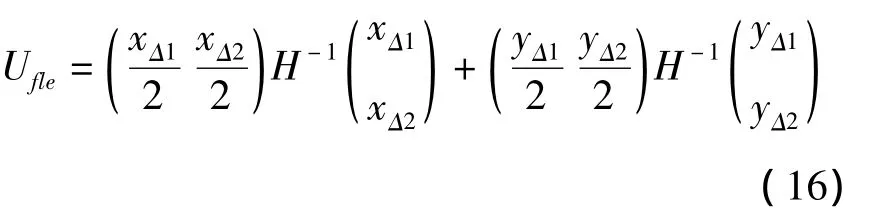
方程(15)可进一步写为
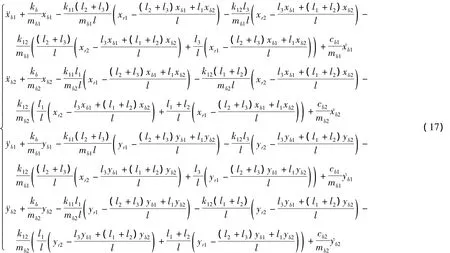
记ω0为系统基频,Rl为转轴半径,引入无量纲参量:
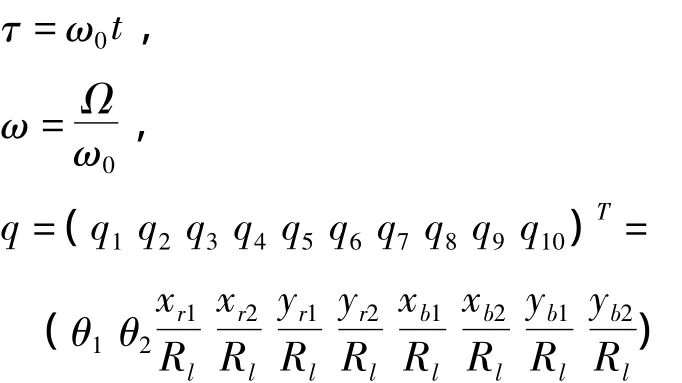
代入运动方程(12)、(14)和(17),整理可无量纲运动微分方程:
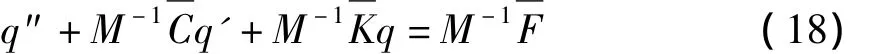
式中,q'为变量q对无量纲时间τ求导.方程(18)中的无量纲刚度矩阵为:

其中无量纲广义力向量为的分量为:
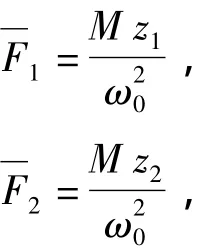
无量纲刚度矩阵分量为:
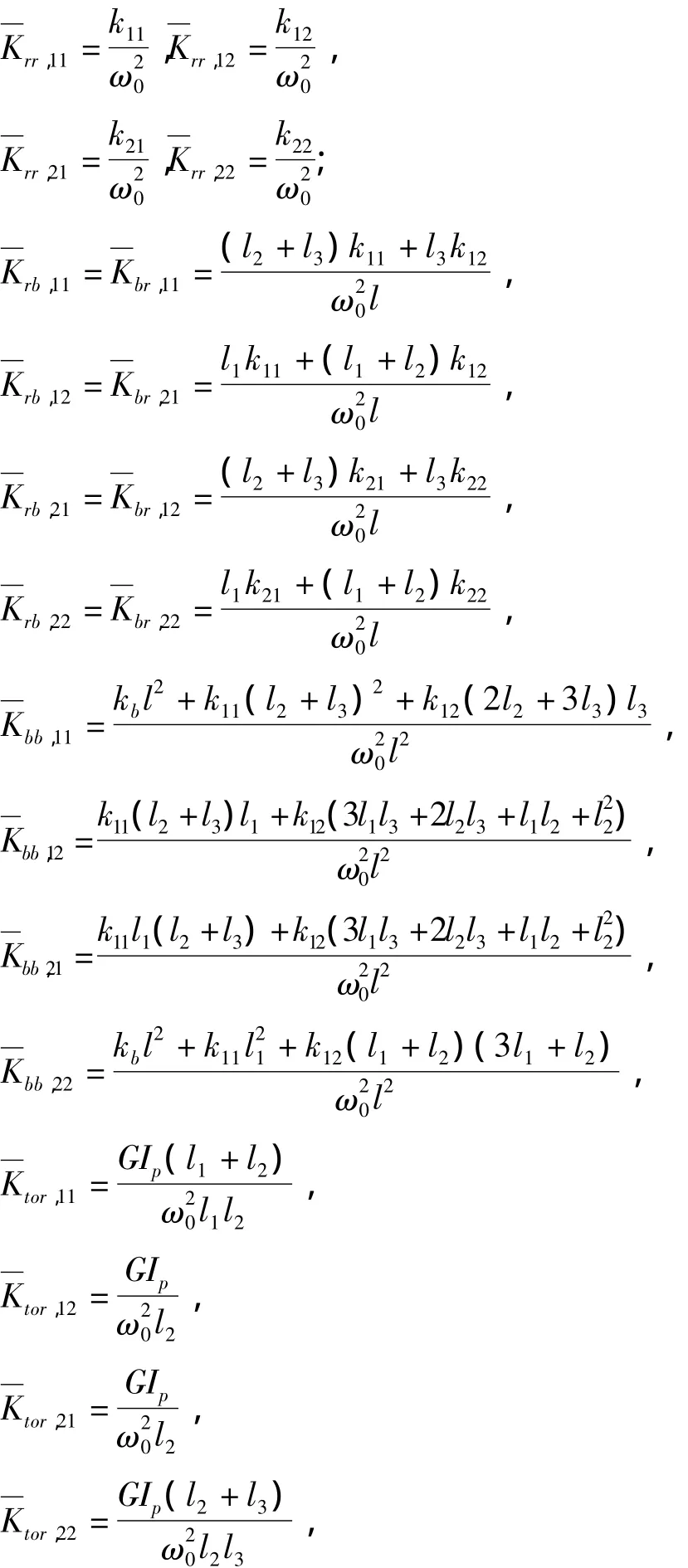
4 面摩擦力矩对扭振的影响
较大的温度梯度所引发的转子轴向窜动可能导致转静件盘面接触以及挤压,由此产生的盘面摩擦力是改变整个系统动力学行为的重要因素.当转盘i处的挤压量δi≥0时(δi=0仅发生盘面接触,摩擦力为零),在该转盘处将发生转静盘面接触挤压与摩擦.同时产生作用在转盘形心并与轴向方向平行的周期激励扭矩,引起转轴的扭转振动.

表1 转子系统参数Table 1 Parameters of rotor system
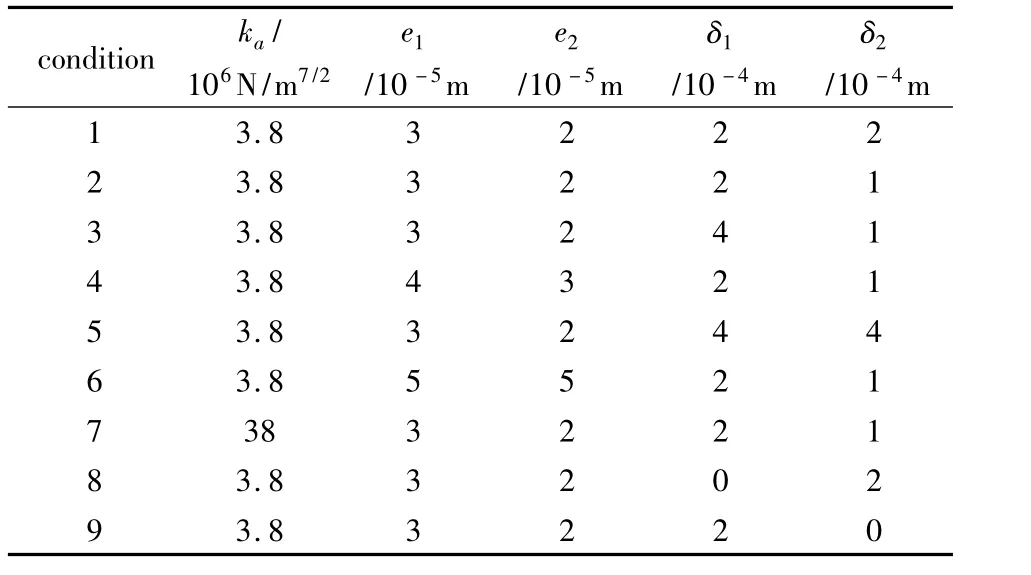
表2 不同工况下双盘转子系统的参数选取Table 2 Parameter selection of double-disk rotor system in different working condition
为了考察不同工作参数对双盘转子系统扭转振动的影响,采用四阶Runge-Kutta积分法对转子动力学无量纲运动微分方程进行数值求解.选取系统参数如表1所示,这里针对不同工况分9组(见表2)分别进行计算.定义响应s(t)的幅值为:
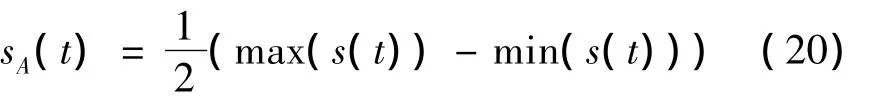
响应s(t)的振动平均位置smean(t)为:
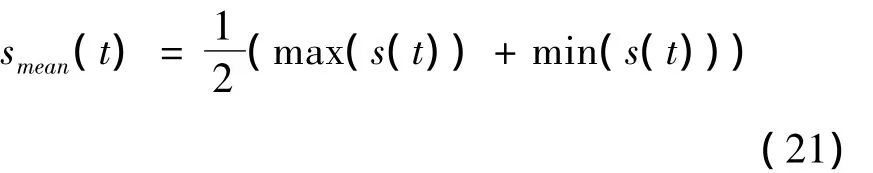
则各工况下扭振响应的幅值与平均位置可以通过数值积分得到,其结果列于表3.
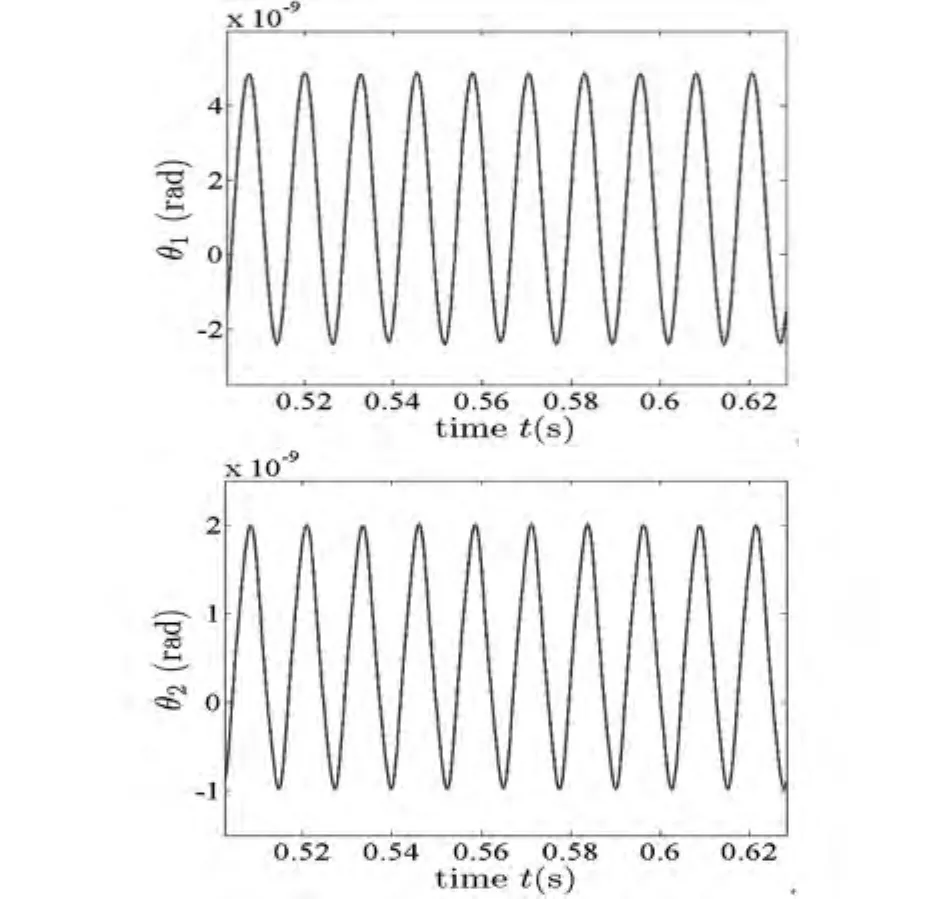
图5 转盘扭转振动的稳态相应(工况1)Fig.5 Response of torsional vibration of disks(working condition 1)
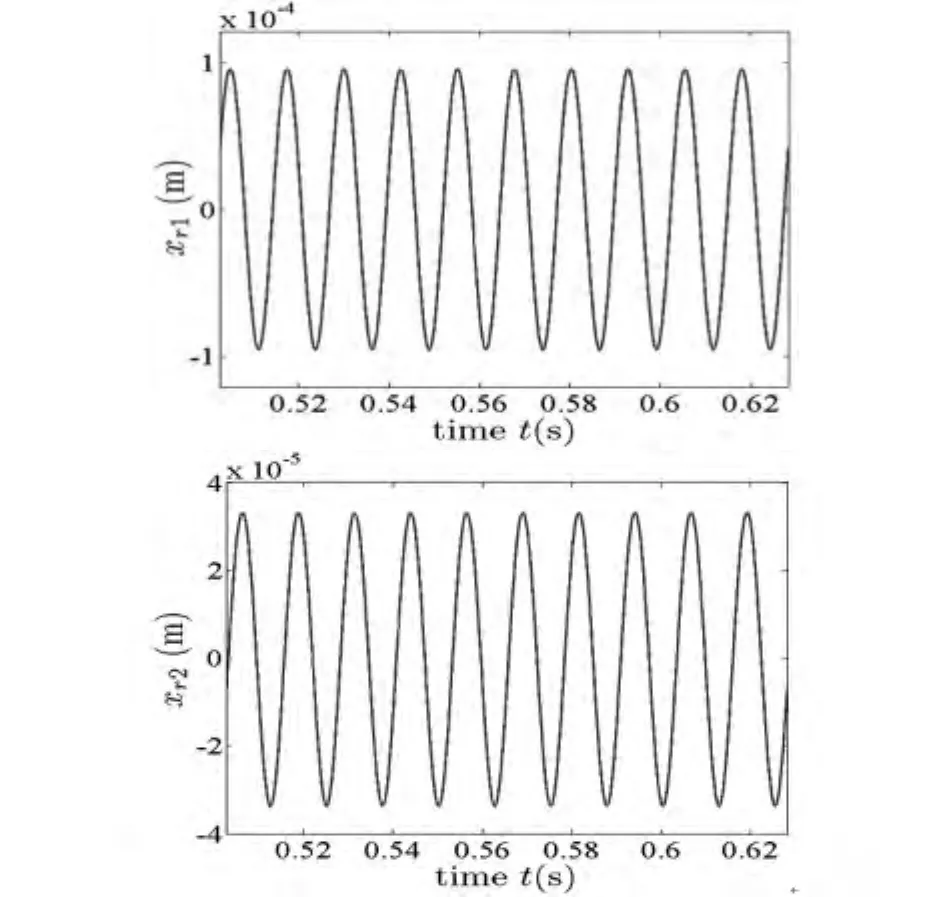
图6 转盘中心的弯曲振动稳态相应(工况1)Fig.6 Flexural vibration of disks(working condition 1)
从转盘处的振动响应(图5、图6)图上可以看出扭转响应的量级是毫秒级,而弯曲振动响应的幅值是丝米级,相比而言扭转振动响应的影响很小.图7给出了给定挤压量条件下由于轴向窜动而引起的摩擦力矩.从表3-4可以看出:比较数组1与数组2,增加转盘2处的挤压量将增加2处摩擦扭矩,进而增加了该处的扭振幅值,而转盘1处的扭振影响较小;比较数组2、3,当转盘1处的挤压量较大时,转盘1与2处扭振的幅值与平衡位置均随之增加,且对转盘1处的影响较明显;比较数组2、4与6,当转盘处的偏心距增加时,偏心激振力增加,将影响双盘转子系统弯曲振动,间接地改变扭矩激励,但对转盘扭转振动的影响较小.
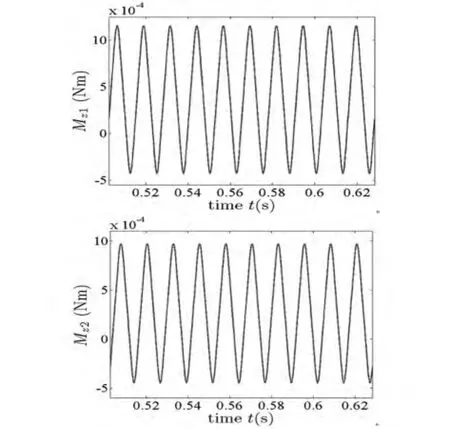
图7 转盘中心处受到的扭矩激励(工况1)Fig.7 Moment exciting on disk center(Working condition 1)
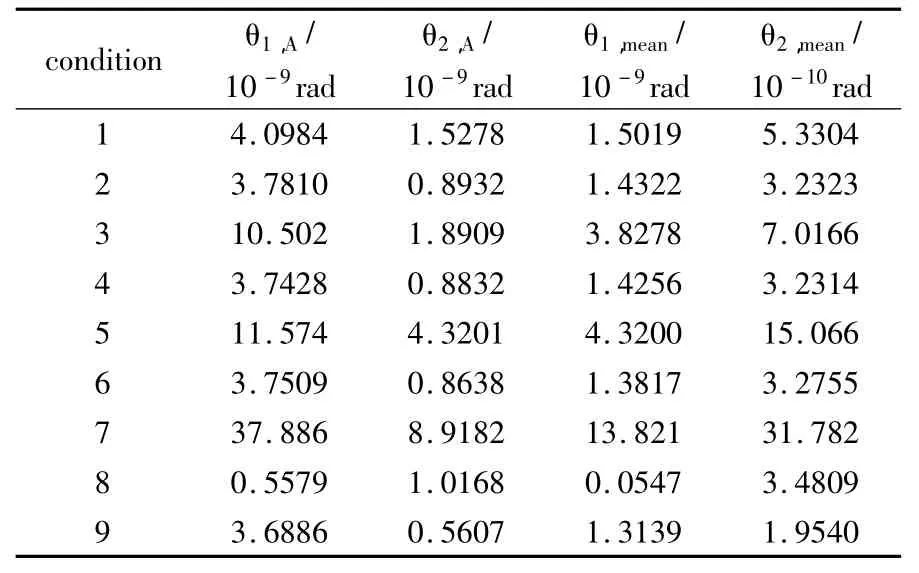
表3 不同工况下扭振对照Table 3 Torsional vibration comparation of different working condition
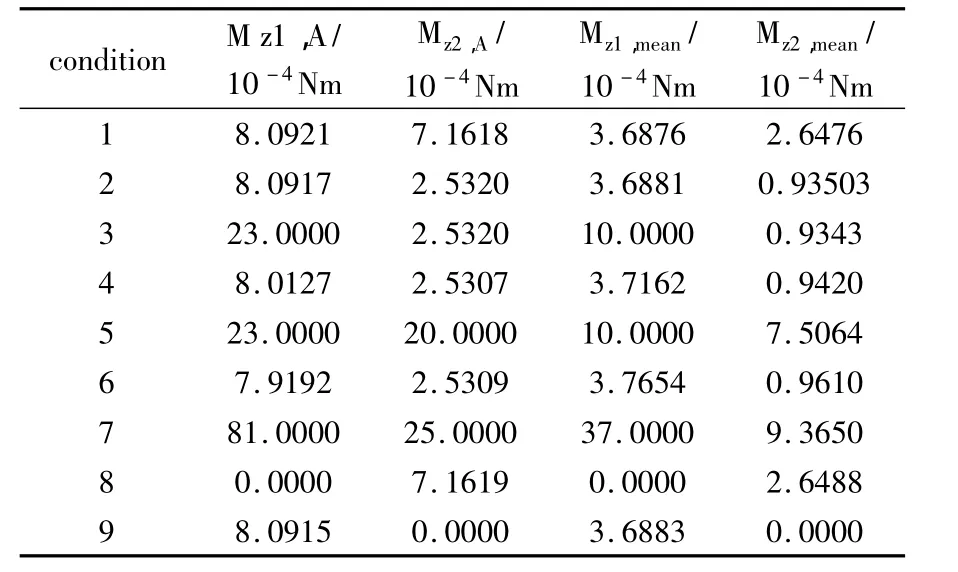
表4 不同工况下的扭矩对照Table 4 Torsional moment comparation of different working condition
比较数组2、5与7,当增加面接触刚度,或转静盘面处挤压量值较大时,摩擦扭矩随之加大,将造成较为严重的扭转振动;从数组8与9可以看出,当仅仅一个转盘发生摩擦,另一处扭矩为零时,扭转振动的幅度较小,且无摩擦扭矩的转盘将产生被动扭振,扭振幅值较存在摩擦的转盘约小一个量级,故其影响可以忽略.因此扭转振动的幅值随周期摩擦激励的增加而增加.
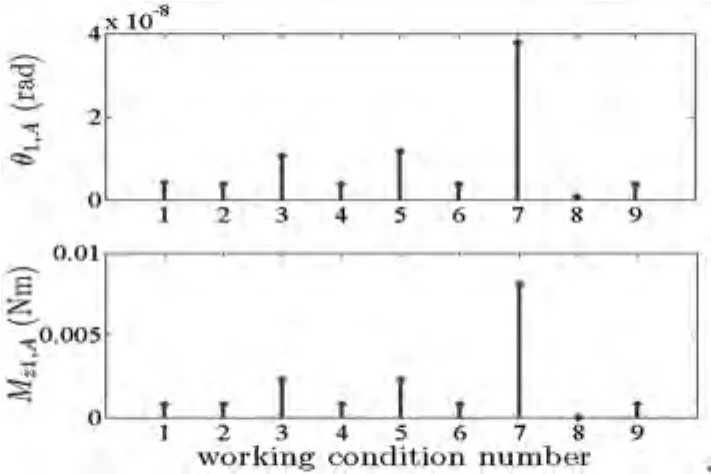
图8 扭振响应与扭矩激励响应幅值(转盘1)Fig.8 Amplitude values of torsional response and moment exciting(disks-1)
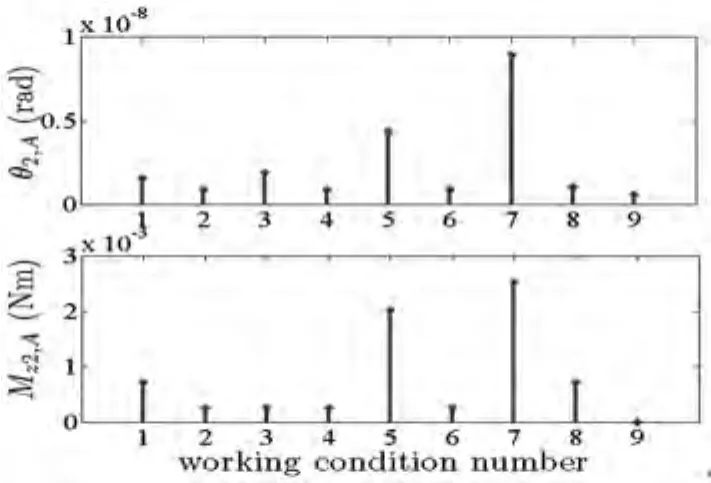
图9 扭振响应与扭矩激励响应幅值(转盘2)Fig.9 Amplitude values of torsional response and moment exciting(disks-2)

图10 扭振响应与扭矩激励均值(转盘1)Fig.10 Mean values of torsional response and moment exciting(disks-1)
比较图8~11,可以看出扭转振动的幅值与均值,与其相对应的摩擦扭矩具有同步变化规律,扭振的平均位置受该处摩擦扭矩的均值制约,即当忽略掉轴承处的扭矩而将两端视为扭转固定端时,双转盘处受扭矩均值的作用将对轴系产生静扭转量,直观上造成双盘的扭转搓动效果.
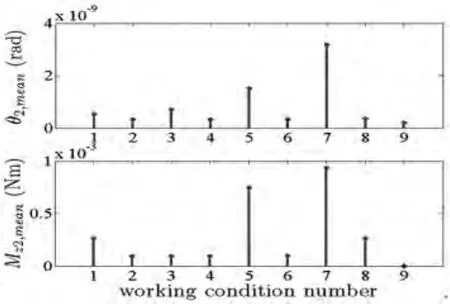
图11 扭振响应与扭矩激励均值(转盘2)Fig.11 Mean values of torsional response and moment exciting(disks2)
5 结论
温度非均匀分布是航空发动机转子的典型运行环境.转静部件的热膨胀系数不一致以及非均匀温度场,导致转盘轴向位移以及转静件轴向间隙的改变是产生轴向碰摩的重要因素之一.本文将航空发动机主转子结构近似为双盘转子-支承系统,并研究了不平衡激振力与盘面摩擦力、摩擦力矩对转子系统扭转振动的影响.
通过对参数化转子系统的动力学仿真分析,验证了转轴轴向热变形产生的盘面接触与摩擦是导致转子轴系产生扭转振动的关键因素;并阐明了基于转盘轴向窜动的面摩擦作用下双盘转子模型所具有的工程意义,利用本文所推导的动力学模型可以估算扭转振动的幅值以及平衡位置.在温度梯度一定的条件下,合理的轴向间隙设计可以控制轴向窜动与摩擦振动,降低转轴的扭转疲劳程度、延长整机机组使用寿命、避免机械失效与经济损失.为旋转机械转子系统的结构设计提供理论支持和安全保障,也拓宽了摩擦转子系统的研究领域.
1 刘长福,邓明.航空发动机结构分析.西安:西北工业大学出版社,2006:1~5(Liu C F,Deng M.Structural analysis of aero engines.Xi’an:Northwestern Polytechnical University Press,2006:1~5(in Chinese))
2 Guha A.Optimization of aero gas turbine engines.The Aeronautical Journal,2001,105(1049):340 ~358
3 Cumpsty N A.Jet propulsion.Cambridge University Press,1997
4 Gordon C Oates.Aircraft propulsion systems technology and design.AIAA Education Series,1989
5 Lee C W.Vibration analysis of rotors.Kluwer Academic Publishers,1993
6 李渤仲等.内燃机轴系扭转振动.北京:国防工业出版社,1984(Li B Z,et al.Torsional vibration of the internal combustion engine.Beijing:National Defense Industry Press,1984(in Chinese))
7 刘英哲.汽轮发电机组扭振.北京:中国电力出版社,1997(Liu Y Z.Turbine generator torsional vibration.Beijing:China Electric Power Press,1997(in Chinese))
8 廖伯瑜,周新民,尹志宏.现代机械动力学与工程应用.北京:机械工业出版社,2003(Liao B Y,Zhou X M,Yin Z H.Modern mechanical dynamics and engineering applications.Beijing:Machinery Industry Press,2003(in Chinese))
9 晏水平,黄树红.汽轮发电机组转子温度分布对其扭转振动的影响.中国电机工程学报,2000,20(11):0010~0013(Yan S P,Huang S H.Impact of temperature distribution on the torsional vibration of turbo generator rotors.Proceedings of the CSEE,2000,20(11):0010~0013(in Chinese))
10 马建敏,韩平畴.柔性联轴器刚度非线性对扭转振动的影响.振动与冲击,2005,24(4):0006~0008(Ma J M,Han P T.Flexible coupling stiffness of nonlinear effects on torsional vibration.Journal of Vibration and Shock,2005,24(4):0006~0008(in Chinese))
11 Lefebvre A H.Gas turbine combustion.McGraw-Hill Co,1983
12 潘健智,曹登庆,初世明等.热膨胀诱导的转子轴向窜动与摩擦振动.航空动力学报,2013,28(5):0989~0999(Pan J Z,Cao D Q,Chu S M et al.Axial displacement and rubbing vibration of rotor system caused by thermal expansion.Journal of Aerospace Power,2013,28(5):0989~0999(in Chinese))
13 Pan J Z,Cao D Q,et al.Analysis on axial displacements of an engine main shaft in complex temperature environments.Applied Mechanics and Materials,2012,226 ~228:714~719
14 张昆鹏,丁千.轴向摩擦转子的弯扭耦合振动分析.中国机械工程,2009,20(21):2526~2531(Zhang K P,Ding Q.Lateral and torsional vibrations of a two-disk rotorstator system with axial contact/rubs.International Journal of China Machanical Engineering,2009,20(21):2526~2531(in Chinese))
*The project supported by the Natural Science Foundation of China(91216106)
† Corresponding author E-mail:dqcao@hit.edu.cn
FLEXURAL-TORSIONAL VIBRATION ANALYSIS OF A DOUBLE-DISK ROTOR CAUSED BY THERMAL EXPANSION INDUCED AXIAL MOVEMENT*
Pan Jianzhi Cao Dengqing†Chu Shiming
(Harbin Institute of Technology,PO Box137,Harbin150001,China)
Taking the structural characteristics and the complexity operating environment of the whole aero-engine system as the research background,the Lagrange approach was employed to establish the flexural-torsional dynamic model for a double-disk rotor subjected to the influence of imbalance exciting force and axial movement caused by the thermal expansion.Due to the axial movement of the shaft caused by the non-uniform distribution of temperature and thermal expansion properties,the analytical expressions of the surface rubbing force and moment were derived respectively.Finally the fourth-order Runge-Kutta method was adopted to solve the dynamic model.Numerical analysis on the dynamical response of the system shows that the temperature stress accumulated by thermal expansion,axial movement of the shaft,and surface rubbing moment,are all the key factors,which would change the inherent physical properties and cause flexural-torsional vibration of the double-disk rotor.
double-disk rotor, rubbing vibration, surface rubbing moment, flexural-torsional vibration,rotor dynamic
18 June 2013,
24 June 2013.
10.6052/1672-6553-2014-027
2013-06-18 收到第 1 稿,2013-06-24 收到修改稿.
*国家自然科学基金资助项目(91216106)
E-mail:dqcao@hit.edu.cn

