基于无网格自然邻接点Petrov-Galerkin法求解带源参数瞬态热传导问题*
李庆华 陈莘莘
(华东交通大学土木建筑学院,南昌 330013)
基于无网格自然邻接点Petrov-Galerkin法求解带源参数瞬态热传导问题*
李庆华 陈莘莘†
(华东交通大学土木建筑学院,南昌 330013)
基于无网格自然邻接点Petrov-Galerkin法,本文建立了一种求解带源参数瞬态热传导问题的新方法.为了克服移动最小二乘近似难以准确施加本质边界条件的缺点,采用了自然邻接点插值构造试函数.在局部多边形子域上采用局部Petrov-Galerkin方法建立瞬态热传导问题的积分弱形式.这些多边形子域可由Delaunay三角形创建.时间域则通过传统的两点差分法进行离散.最后通过算例验证了该数值算法的有效性和正确性.
热传导问题, 源参数, 无网格法, 局部Petrov-Galerkin法, 自然邻接点插值
引言
随着时间变化,不同场点上的温度场随时间而变化,这种传热问题被看作瞬态热传导问题.瞬态热传导问题是实际工程中十分普遍的现象,很多学者都对其进行了分析.由于结构的形状以及变温条件的复杂性,要精确地确定温度场主要依赖于数值模拟的方法[1-2].近年来,随着无网格方法的迅速发展,无网格方法正以其独特优势在热传导问题的研究中得到了广泛的应用[3-7].
无网格自然邻接点 Petrov-Galerkin 法[8,9]本质上是基于自然邻接点插值的无网格局部Petrov-Galerkin(Meshless Local Petrov-Galerkin,MLPG)法.这种方法不仅具有自然元法易于施加本质边界条件的优点,而且还具有MLPG法的一些优良特性.在这种方法中,任意节点的子域是由以该节点为公共顶点的Delaunay三角形构成的多边形区域.此外,采用有限元法的三节点三角形单元的形函数作为权函数,可以降低域积分中被积函数的阶次,提高了计算效率.本文尝试将无网格自然邻接点Petrov-Galerkin法应用于带源参数瞬态热传导问题的求解计算.首先通过变换将此类带源参数的热传导问题转化为标准的热传导控制方程形式,然后基于无网格自然邻接点Petrov-Galerkin法理论详细推导了相应的计算公式.最后,典型算例的计算和对比分析验证了应用无网格自然邻接点Petrov-Galerkin法分析带源参数瞬态热传导问题的有效性.
1 自然邻接点插值
自然邻接点插值是基于著名的Voronoi结构和Delaunay三角形网格.按插值基函数的不同,自然邻接点插值可分为 Sibson 插值[8-10]和 Laplace插值[11-14].本文采用 Sibson 插值.
一阶Voronoi结构定义:到节点xI的距离小于到其它任何节点xJ的距离的区域的集合.其数学表达为

式中,d(x,xI)为点x与节点xI的距离.此外,二阶Voronoi结构TIJ的数学表述为:

在几何意义上,TIJ是那些以xI为最近点,以xJ为第二近点的空间点的位置集合.
当采用Sibson插值时,点x对节点xI的形函数φI(x)定义为

式中,AI(x)为点x与节点xI的二阶Voronoi结构TxI的面积.
定义了各节点的插值函数后,点x的温度类似于有限元法可写为

式中,uI(I=1,2,…,n)是点x周围自然邻节点I的温度,φI(x)为对应节点的形函数.
2 控制方程及其局部弱形式
考虑如下的带源参数p(t)的二维瞬态热传导问题


初始条件为

边界条件为

式中,p,φ,f,g0,g1,h0,h1为已知函数;u是未知函数.
为了将带源参数p(t)的热传导问题转化为标准的热传导控制方程形式,作变换[5-7]
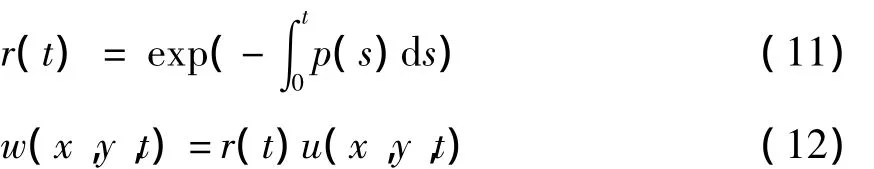
方程(5)变为

初始条件为
边界条件为

经过这个变换,源参数p(t)消失了,我们可以把式(13)~(18)当成标准的瞬态热传导问题进行求解.
将问题域及其边界用N个节点离散,在任意节I点对应的子域ΩIs上,平衡方程式(13)的局部弱形式可以写为

式中,vI为加权函数.
对方程(19)的左边项进行分部积分并利用散度定理后,可得
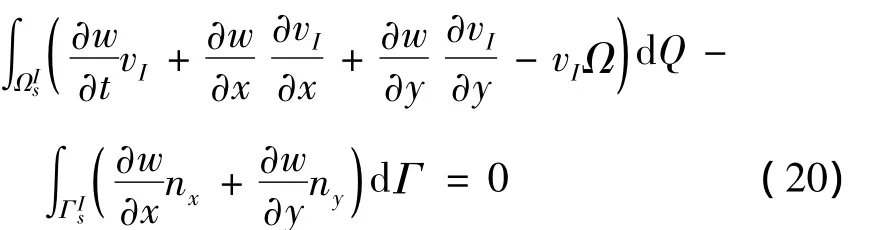
式中,Q=r(t)φ(x,y,t).在无网格自然邻接点Petrov-Galerkin 法中,子域是由共享节点I的Delaunay三角形TIi构成,如图1所示.为了简化计算,采用有限元法的三节点三角形单元的形函数作为权函数,并注意到式(15)~(18)中无自然边界条件,方程(20)可改写为:

图1 局部多边形子域Fig.1 The local polygonal sub - domains

由于只对空间域进行离散,求解域Ω内的试函数w(x,t)可由式(4)表示为

将式(22)代入式(21)可得如下的离散方程

方程(23)是一组以时间为独立变量的线性常微分方程组.本文采用传统的两点差分法求解方程(23).对给定的时间步长Δt,取插值公式

式中,θ是可以自由选择的时间加权系数,不同的取值对应不同的时间差分格式.本文取θ=2/3.


3 算例分析
为了验证本文提出的求解带源参数瞬态热传导问题数值方法的有效性,本文给出了具体的算例.
考虑问题(5)~(10),其中



图2 节点布置Fig.2 Node distribution

图 3 u(x,y,t)的数值解和解析解Fig.3 The numerical and exact solution of u(x,y,t)
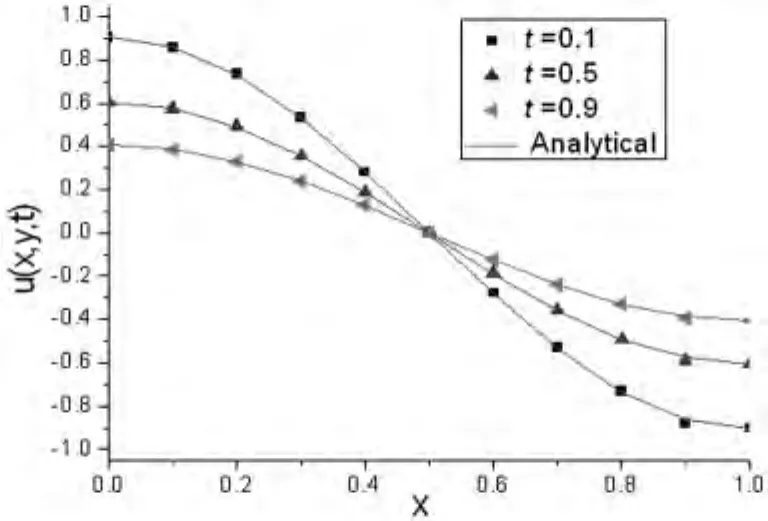
图 4 u(x,y,t)的数值解和解析解Fig.4 The numerical and exact solution of(x,y,t)
我们利用无网格自然邻接点 Petrov-Galerkin法对上述带源参数瞬态热传导问题进行求解.如图2所示,在求解域内均匀布置了121个节点.进行数值积分时,在构成子域的每个Delaunay三角形上布置3个高斯点.时间步长取为Δt=0.001.图3给出了函数u(x,y,t)在t=0.1,0.5 和 0.9 时刻y=0.6处的解析解和数值解.图4给出了函数u(x,y,t)在t=0.1,0.5 和0.9 时刻x=0.5 处的解析解和数值解.通过图3和图4可以看出,本文提出的无网格自然邻接点Petrov-Galerkin法计算得到的数值解和解析解吻合很好.
4 结论
无网格自然邻接点Petrov-Galerkin法作为一种无网格方法,不需要对求解域进行网格划分,前处理简单.由自然邻接点插值创建的形函数满足Kronecker delta函数性质,从而能够直接准确地施加本质边界条件.此外,采用有限元法的三节点三角形单元的形函数作为权函数,可以降低域积分中被积函数的阶次,提高了计算效率.本文建立了一种基于无网格自然邻接点Petrov-Galerkin法的带源参数瞬态热传导问题分析方法,并推导了相应的计算公式.数值算例表明,用无网格自然邻接点Petrov-Galerkin法求解带源参数瞬态热传导问题是可行的,具有节点布置灵活、前处理简单、计算简便等优点.
1 Rashid Y R.Analysis of axisymmetric composite structures by the finite element method.Nuclear Engineering and Design,1996,3(1):163~182
2 Dargush G F,Banerjee P K.Application of the boundary element method to transient heat conduction.International Journal for Numerical Methods in Engineering,1991,31:1231~1244
3 Li Q H,Chen S S,Kou G X.Transient heat conduction analysis using the MLPG method and modified precise time step integration method.Journal of Computational Physics,2011,230:2736~2750
4 Li Q H,Chen S S,Zeng J H.A meshless model for transient heat conduction analyses of 3D axisymmetric functionally graded solids.Chinese Physics B,2013,22(12):120204
5 王峰,林皋,郑保敬,刘俊,李建设.带源参数热传导问题的基于滑动Kriging插值的MLPG法.力学季刊,2013,34(2):175~180(Wang F,Lin G,Zheng B J,Liu J,Li J S.Meshless local Petrov-Galerkin method with moving Kriging interpolation for solving heat conduction problems with source parameter.Chinese Quarterly of Mechanics,2013,34(2):175~180(in Chinese))
6 程荣军,程玉民.带源参数的二维热传导反问题的无网格方法.力学学报,2007,39(6):843~847(Cheng R J,Cheng Y M.The meshless method for a two-dimensional inverse heat conduction problem with a source parameter.Acta Mechanica Sinica,2007,39(6):843 ~ 847(in Chinese))
7 程荣军,程玉民.带源参数的热传导反问题的无网格方法.物理学报,2007,56(10):5569~5574(Cheng R J,Cheng Y M.The meshless method for solving the inverse heat conduction problem with a source parameter.Acta Physica Sinica,2007,56(10):5569 ~ 5574(in Chinese))
8 蔡永昌,朱合华,王建华.基于Voronoi结构的无网格局部Petrov-Galerkin法.力学学报,2003,35(2):187~193(Cai Y C,Zhu H H,Wang J H.The meshless local Petrov-Galerkin method based on the Voronoi cells.Acta Mechanica Sinica,2003,35(2):187 ~193(in Chinese))
9 Cai Y C,Zhu H H.A meshless local natural neighbour interpolation method for stress analysis of solids.Engineering Analysis with Boundary Elements,2004,28:607~613
10 Sukumar N,Moran B,Belytschko T.The natural element method in solid mechanics.International Journal for Numerical Methods in Engineering,1998,43:839~887
11 Sukumar N,Moran B,Semenov Y.Natural neighbour Galerkin method.International Journal for Numerical Methods in Engineering,2001,50:1~27
12 Zhu H H,Liu W J,Cai Y C,Miao Y B.A meshless local natural neighbour interpolation method for two-dimensional incompressible large deformation analysis.Engineering Analysis with Boundary Elements,2007,31,856~862
13 李晓龙,王复明,徐平.自然元与无限元耦合方法在岩土工程粘弹性分析中的应用.振动与冲击,2008,27(12):117~121,184(Li X L,Wang F M,Xu P.Coupling method of natural and infinite element for visco- elastic analysis in geotechnical engineering.Journal of Vibration and Shock,2008,27(12):117 ~ 121,184(in Chinese))
14 王卫东,张敦福,赵国群,程钢.基于偶应力理论的自然单元法研究.机械强度,2009,31(4):634~637(Wang W D,Zhang D F,Zhao G Q,Cheng G.Study on natural element method based on couple stresses theory.Journal of Mechanical Strength,2009,31(4):634~637(in Chinese))
*The project supported by the Foundation of Hunan Educational Committee(12C0059)
† Corresponding author E-mail:chenshenshen@tsinghua.org.cn
ANALYSIS OF TRANSIENT HEAT CONDUCTION PROBLEMS WITH A SOURCE PARAMETER BASED ON MESHLESS NATURAL NEIGHBOUR PETROV-GALERKIN METHOD*
Li Qinghua Chen Shenshen†
(School of Civil Engineering and Architecture,East China Jiaotong University,Nanchang330013,China)
Based on meshless natural neighbour petrov-Galerkin method,a novel meshless method was developed to solve transient heat conduction problems with a source parameter.The essential boundary conditions cannot be enforced directly when the non-interpolative moving least squares(MLS)approximation is used.In order to overcome this difficulty,the natural neighbour interpolation was employed instead of the moving least squares approximation to construct trial functions.The local weak forms of the transient heat conduction problems were satisfied locally in a series of polygonal sub-domains,which can be constructed easily with Delaunay tessellations.The traditional two-point difference technique was selected for the time discretization scheme.A numerical example demonstrates the validity and effectiveness of the presented method.
heat conduction problems, source parameter, meshless method, local Petrov-Galerkin method,natural neighbour interpolation
12 February 2014,
25 February 2014.
10.6052/1672-6553-2014-022
2014-02-12 收到第 1 稿,2014-02-25 收到修改稿.
*湖南省教育厅科研项目资助(12C0059)
E-mail:chenshenshen@tsinghua.org.cn

