含外力项时变系数KdV方程与时变系数耦合KdV方程组的孤子解*
杨绍杰 化存才
(云南师范大学数学学院,昆明 650500)
含外力项时变系数KdV方程与时变系数耦合KdV方程组的孤子解*
杨绍杰 化存才†
(云南师范大学数学学院,昆明 650500)
应用孤子拟解法研究了含外力项时变系数KdV方程与一类时变系数耦合KdV方程组.首先将方程经过变量代换转换为齐次方程,然后将孤子解假设为双曲正割函数的形式带入方程或方程组,最后借助Maple软件完成复杂的计算来确定假设的孤子解的待定系数,从而得到孤子解存在的条件及其孤子解.结果显示:孤子拟解法计算简便且能得到方程的亮孤子解.
KdV方程, 耦合KdV方程组, 变系数, 孤子拟解法
引言
寻找非线性偏微分方程的精确解是许多数学家和物理学家较为关注的研究课题,一些有效的求解方法已经被提出,如著名的反散射方法,Hirota方法,Bäcklund变换,齐次平衡法,F展开法,孤子拟解法等[1-4].由于变系数非线性偏微分方程能更好的描述物理现象,所以变系数偏微分的研究引起越来越多学者的关注[5-12].KdV 方程可以用来描述等离子体的磁流体波运动、弹性杆中纵向色散波及弱非线性回复力的浅水波等重要的物理现象,耦合的KdV方程组通常来描述两个长波的相互影响.如果考虑水深可变和出现涡旋可压缩流体的运动规律就需要变系数KdV方程和变系数耦合KdV方程组来描述,因此研究变系数KdV方程和变系数耦合KdV方程组有重要的意义.孤子拟解法通常用来求方程的亮孤子解[5-7],对此,本文考虑将孤子拟解法应用于含外力项时变系数KdV方程和时变系数耦合KdV方程组中.
本文考虑如下含外力项时变系数KdV方程
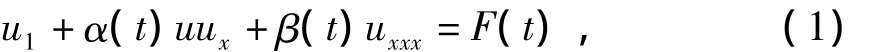
其中 α(t),β(t),F(t)为时间t的函数,F(t)为外力项.
和时变系数耦合KdV方程组
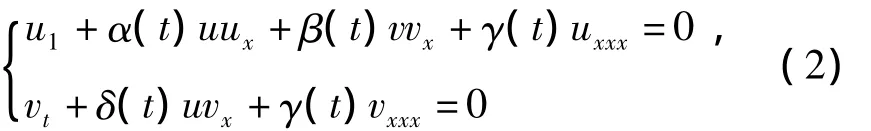
其中 α(t),β(t),δ(t),γ(t)为时间t的函数.
当F(t)=0时,方程(1)为时变系数KdV方程,时变系数的KdV已有很多学者研究[6-8].
方程组(2)可以认为是一个简单的广义Hirota-Satsuma和 KdV 方程的耦合[9].文献[10]利用 F展开法研究了方程组(2)的周期波解,文献[11]利用对称理论研究了方程组(2)的相似约化和精确解.
在本文中,我们首先研究含外力项时变系数KdV方程(1),利用一个变换将方程(1)变为齐次方程,通过孤子拟解法得到齐次方程的孤子解从而得到了方程(1)的孤子解,然后将孤子拟解法应用到时变系数耦合KdV方程组(2),得到了孤子解.
1 含外力项时变系数KdV方程的孤子解
首先作如下变量变换:
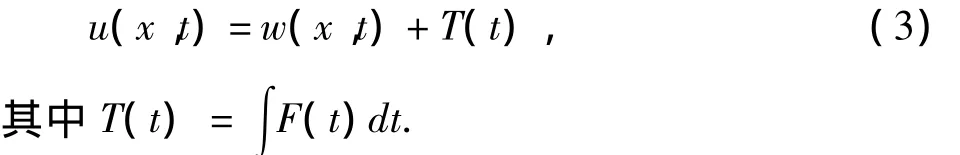
将其代入方程得
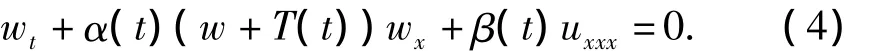
我们首先求(4)的解进而得到(1)的解,为了得到方程(4)的解,我们假设方程(4)的解有如下形式:
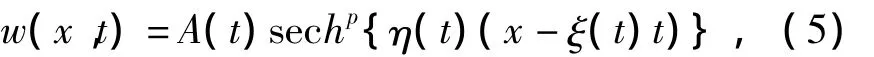
其中A(t)为波幅,η(t)为波数,ξ(t)为波速都是关于时间t的待定函数,p为待定常数.
由假设(5)我们得到
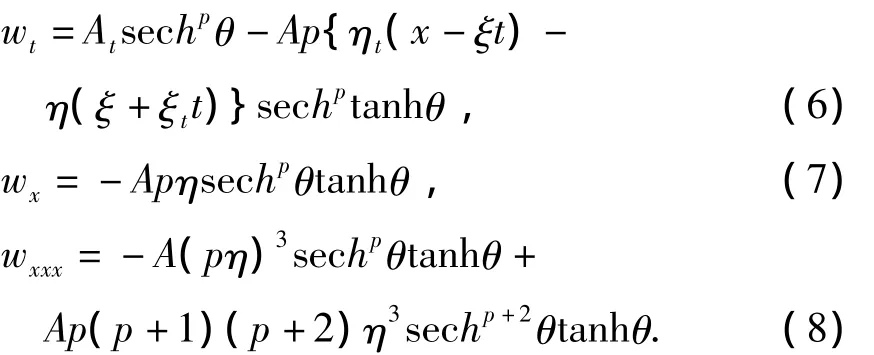
将(5)~(8)代入(4)得到:
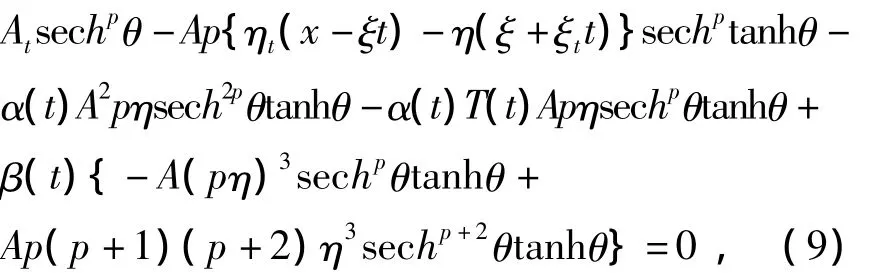
平衡(9)中 sech2pθtanhθ和 sechp+2θtanhθ的指数得到:
所以有p=2.
将p=2代入(9)令 sech4θtanhθ的系数为0,得

于是,由(11)式得到波数

再令 sech2θtanhθ的系数为 0,得
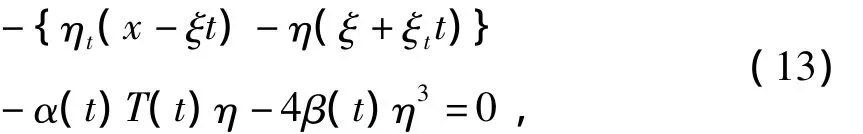
考虑到η,ξ都是t的函数,那么(13)可以得到等价于如下两个方程:
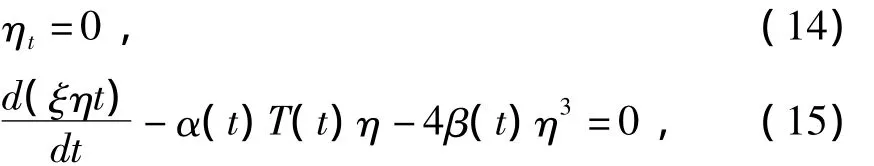
解(14)(15)得
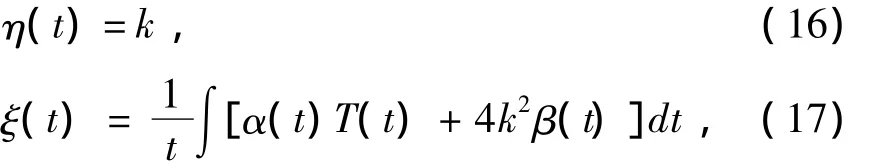
最后令(9)(11)中sech2θ的系数为0,那么有

于是,由(18)得到

其中A0为任意常数.
要使(12)(16)两式 η 相等,所以 α,β,A0,k需满足如下关系

这样,我们得到了方程(4)的孤子解
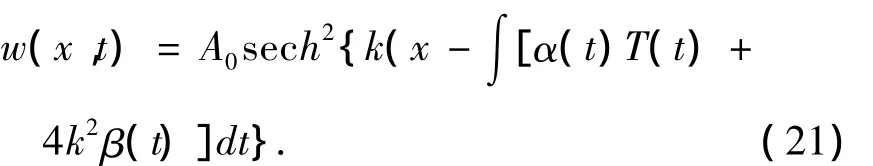
再经过变量变换(3)就得到时变扰力作用下变系数KdV方程(1)的解
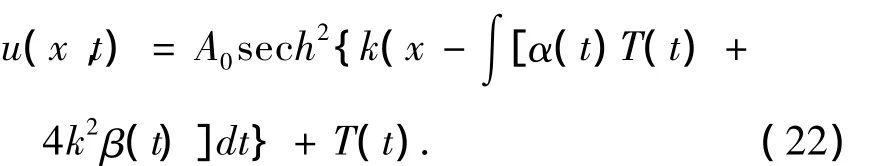
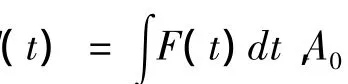
当F(t)=0时,即没有外力作用时,(22)变为变系数KdV方程的亮孤立子解.
2 时变系数耦合KdV方程组的孤子解
为了得到方程组(2)的亮孤立子解,我们假设方程组(2)的解有如下形式:
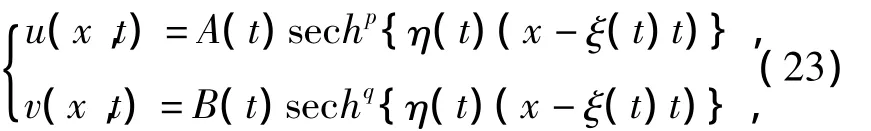
其中A(t),B(t)为波幅,η(t)为波数,ξ(t)为波速都是关于时间t的待定函数,p,q为待定常数.
由假设(23)我们得到

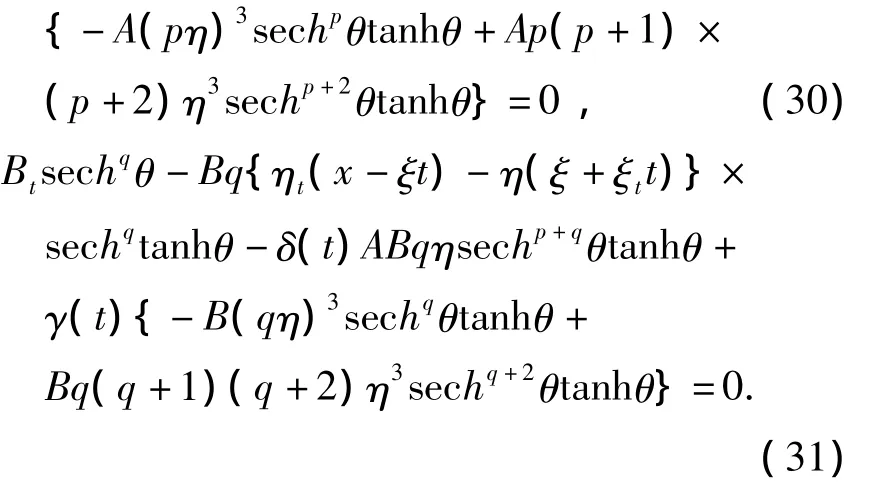
平衡(30)中 sech2pθtanhθ和 sechq+2θtanhθ的指数得

平衡(31)中 sechp+qθtanhθ和 sechq+2θtanhθ的指数得

由(33)(34)得q=2.
将p=2,q=2 代入(30)令 sech4θtanhθ的系数为0,得
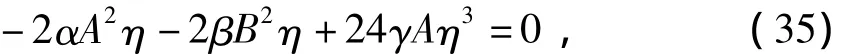
由(35)得

将p=2,q=2 代入(31)令 sech4θtanhθ的系数为0,得
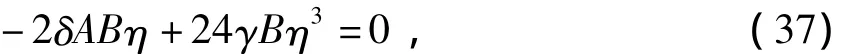
由(37)得

要使(36)(38)中 η 相等,那么需要 α,β,δ,A,B满足如下关系

将p=2,q=2代入(30)(31)令 sech2tanhθ的系数令为 0,得
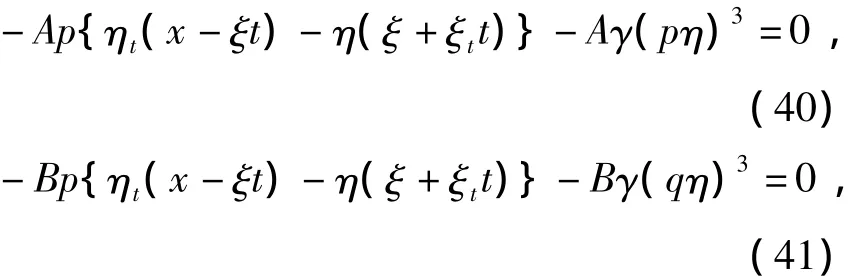
考虑到η,ξ都是t的函数,那么(40)(41)可以得到等价于如下两个方程

解(42)(43)得
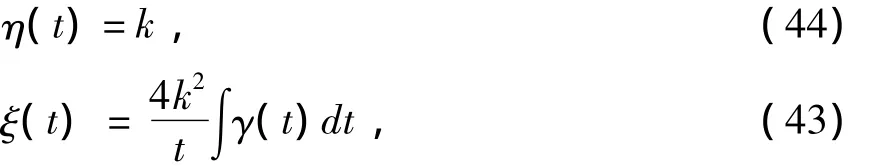
最后,将p=2,q=2代入(30)(31)中令 sechpθ,sechqθ的系数为0,那么有

于是,由(46)(47)得到

其中A0,B0为任意常数.
要使(36)(38)两式中 η 相等,所以 α,β,δ,γ,A0,B0,k需满足如下关系
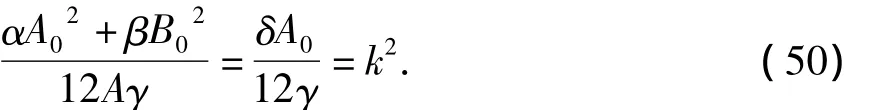
这样,我们就得到了时变系数耦合KdV方程组(2)的亮孤子解:
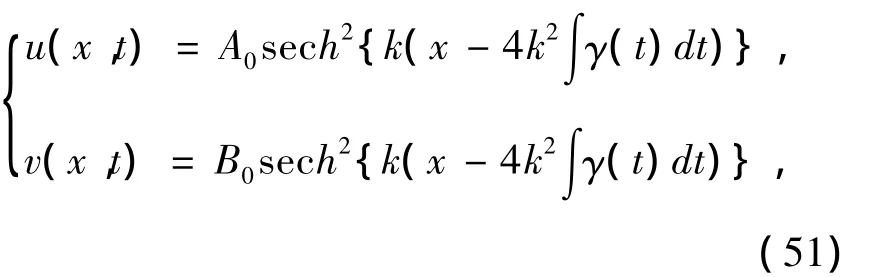
其中 α,β,δ,γ,A0,B0,k满足关系(50).
3 结论
本文研究含外力项变系数KdV方程与时变系数耦合KdV方程组,首先做一个变换将含外力项的变系数KdV方程转化为齐次方程,通过孤子拟解法得到齐次方程的孤子解从而得到了方程含外力项变系数KdV方程的孤子解.然后将孤子拟解法应用到时变系数耦合KdV方程组,得到了孤子解.结果显示,孤子拟解法计算简便且能得到方程的亮孤子解.
1 Hirota R.Exact solutions of the Korteweg-de Viries equation for multiple collisions of solitons.Physics Review Letters,1971,27:1192 ~1194
2 Wahlquist H D,Estabrook F B.Bäcklund transformation for solitons of the Korteweg-de Vries equation.Physical Review Letters,1973,31:1386~1390
3 Wang M L.Application of homogeneous balance method to exact solutions of nonlinear equations in mathematical physics.Physics Letters A,1996,A2:16~67
4 Drazin P G,Johnson R S.Solitions:an introduction.Cambridge:Cambridge University Press,1989
5 Triki H,Wazwaz A M.Bright and dark solutions for a K(m,n)equation with t-dependent coefficient.Physics Letters A,2009,373:2162~2165
6 Wazwaz A M.A study on KdV and Gardener equations with time-dependent cofficents and forcing terms.Applied Mathematics and Computation,2010,217:2277~2281
7 Wazwaz A M,WazwazA M.Solition solutions for a generalized KdV and BBM equations with time-dependent coefficients.Communications in Nonlinear Science NumericalSimulation,2011,16:1122~1126
8 Fan E G.Auto-Bäcklund transformation and similarity reductions for general variable coefficient KdV equations.Physics Letters A,2002,294:26 ~30
9 Hirota R,Satsuma J.Solition solutions of a coupled Korteweg-de Viries equation.Physics Letters A,1981,85:407~408
10 Zhou Y B,Wang M L,Wang Y M.Periodic wave solutions to a coupled KdV equations with variable coefficients.Physics Letters A,2003,308:31~36
11 E M El Gazzy,M H M Moussa,Rehab M El Shikh.New similarity reductions and exact solutions of coupled KdV equations with variable coefficients.International Journal of Nonlinear Science,2009,7:475~484
*The project supported by the Natural Science Foundation of China(11162020),the Planning Program of Leading Youth Scholars of Science and Technology of Yunnan Province of China(2008PY059)
† Corresponding author E-mail:cuncai-hua@139.com
SOLITON SOLUTIONS OF KDV EQUATION AND A COUPLED KDV EQUATION WITH TIME-DEPENDENT COEFFICIENTS AND FORCING TERM*
Yang Shaojie Hua Cuncai†
(School of Mathematics,Yunnan Normal University,Kunming650500,China)
This paper studied the KdV equation with time-dependent coefficients and forcing term and the coupled KdV equations with time-dependent coefficients by using soliton ansaze.Firstly,the equation was converted to homogeneous equation by using a variable transformation.Then,by assuming the soliton solutions to be the form of sech function,and with the help of Maple software,the complicated and tedious calculations were performed,and the conditions of existence of solitons and soliton solutions were obtained.The results show that the calculation of soliton ansaze is simple and can obtain bright soliton solutions.
KdV equation, coupled KdV equations, time-dependent coefficients, soliton ansatz
8 January 2013,
1 May 2013.
10.6052/1672-6553-2013-076
2013-01-08 收到第 1 稿,2013-05-01 收到修改稿.
*国家自然科学基金资助项目(11162020)、云南省中青年学术与技术带头人计划项目(2008PY059)
E-mail:cuncai-hua@139.com

