三嵌段共聚物和两嵌段共聚物在水溶液中共混自组装成多室胶束结构的耗散粒子动力学模拟

徐博深 赵 英 沈显良 丛 悦 殷秀梅王新鹏 苑 青 于乃森 董 斌

(大连民族学院物理与材料工程学院,纳米光子学研究所,辽宁大连116600)

1 Introduction

Hierarchical assembly of materials attracts researchers in both academic and application fields due to their potential applications in the nanoscience.1,2Multiblock copolymers could self-assemble into multicompartment micelles,which have characterized structures of segregated incompatible subdomains and wide applications in the biomedicine,drug delivery,and nanotechnology.3-5The multicompartment micelles are nanoscopic aggregates that possess a hydrophilic shell and one to several compartments in a hydrophobic core.It could perform many distinct functions,for example,in the nanobiotechnology,the separated incompatible compartments of the hydrophobic core could entrap and release various hydrophobic drugs selectively,while the hydrophilic shell would stabilize these nanostructures.5

Since the structures self-assembled from diblock copolymers can only be divided into“core”and“corona”domains,diverse approaches based on triblock copolymers for preparing multicompartment micelles had been developed by several groups.3-10Since the pioneer work by Lodge and co-workers,11most investigations had been focused on the structure of multicompartment micelles formed from star triblock copolymers,which had simulated the field of advanced colloidal systems.They synthesized a series of ABC miktoarm star triblock copolymers in dilute aqueous solution,and visualized various morphologies of multicompartment micelle.11They further demonstrated that two incompatible agents could be separately stored in the discrete subdomains of the multicompartment micelles.12For multicompartment micelles to be most effective in applications,their sizes,shapes,and chemical structures must be controlled precisely.Alot of factors,for example,the structure of the multiblock copolymer and the property of the solution can take the effect on the morphology and structure of the nanoscopic aggregates.However,much progress has been made on the preparation of the multicompartment micelles,the experimental investigation is still not easy.Thus,molecular simulation technique,as a time and cost efficient tool,can not only complement experimental works with a wide parameter space,but also give a preview of phenomena prior to experiments.13-25

In the recent years,dissipative particle dynamics(DPD)simulation method has been a powerful tool for better understanding the self-assembly mechanism of the multicompartment micelles.13For example,Zhong and co-workers13-15used DPD simulation to not only study the formation process of the multicompartment micelles,but also identify the morphologies by varying block lengths,block ratios,and solvent qualities in a systematic way.Chou and Tsao18investigated the effects of molecular architecture,block length,and solution concentration on the morphologies of ABC terpolymers by performing DPD simulations.Furthermore,we studied the influence of the molecular architecture of ABC triblock copolymers and the blend of diblock copolymer and homopolymer on the formation of the multicompartment micelles.19,20However,as a more simple and economical approach,the knowledge of tuning the multicompartment micelles by mixing different types of polymer components is still very little.

Thus,in this work,we focus exclusively on the formation of multicompartment micelles from the mixture of triblock copolymers and diblock copolymers in the dilute aqueous solution by DPD simulations.In this study,the effect of different block lengths of block copolymers is considered(shown in Fig.1 and Table 1).The structures of the multicompartment micelles are then characterized by the density profiles and the pair distribution function.

2 Model and simulation details

DPD is a mesoscopic simulation technique introduced by Hoogerbrugge and Koelman in 1992.26A DPD bead represents a group of atoms or a volume of fluid that is large on the atomistic scale but still macroscopically small.27The force experienced by particle i is composed of three parts:a conservative force FC,a dissipative force FD,and a random force FR.To model the block copolymers,we tie the adjacent beads in a single polymer chain by harmonic spring force FS.Each force is pairwise additive:

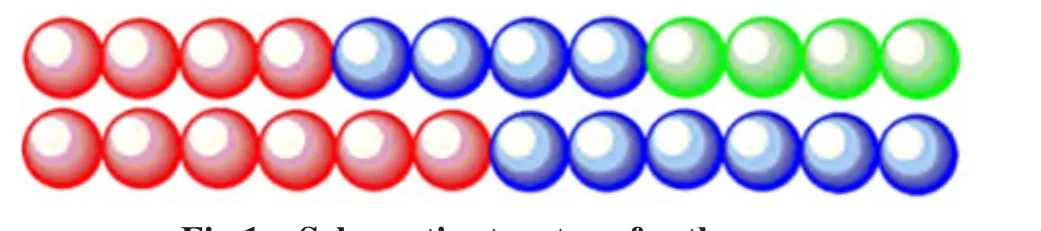
Fig.1 Schematic structure for the one representative model

Table 1 List of twelve blends of triblock copolymer and diblock copolymer

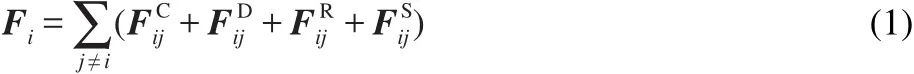
The force FijC,FijD,FijR,runs over all other particles within a certain cutoff radius rc.The different parts of the forces are given by:

where rij=ri-rj,rij=|rij|,eij=rij/rij,riand rjare the positions of particle i and particle j,respectively.vij=vi-vj,viand vjare the velocities of particle i and particle j,respectively.αijis a constant which describes the maximum repulsion between interacting beads.γandσare the amplitudes of dissipative and random forces,respectively.ωC,ωD,andωRare three weight functions for the conservative,dissipative,and random forces,respectively.For the conservative force,we chooseωC(rij)=1-rij/Rcfor rijRc,ωD(rij)andωR(rij)follow a certain relation according to the fluctuation-dissipation theorem,28

Here we choose a simple form ofωDandωRfollowing Groot and Warren,27

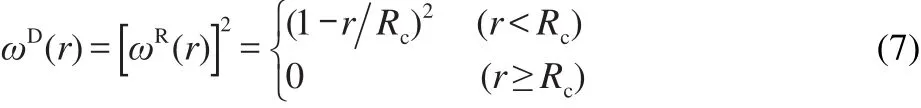
ξijis a random number with zero mean and unit variance,chosen independently for each interacting pair of beads at each time step Δt.A modified version of velocity-Verlet algorithm27is used here to integrate the equations of motion.For easy numerical handling,we have chosen the cutoff radius,the particle mass(m),and the temperature(T)as the units of the simulated system,i.e.,Rc=m=KBT=1.KBis Boltzmann constant.As a consequence,the unit of timeτis τ=Rcm KBT=1.

The conservative interaction strengthαijis chosen according to the linear relation with Flory-Hugginsχparameters by where the interaction parameter between the same type of bead αiiequals 25 to correctly describe the compressibility of water,27andρ=3 is the number density in our simulations.The spring constant C is set to be 4.0,which is enough to keep the adjacent beads connected together along the polymer backbone.29

The work is performed by our parallel DPD program,which has been successfully used to study the self-assembly of block copolymer in the aqueous solution.19,20In literature,Zhong and co-workers15had determined the DPD repulsion parameters between unlike species of ABC block copolymer,consisting of the weakly hydrophobic polyethylethylene(denoted as A),the hydrophilic poly(ethylene oxide)(denoted as B),and the strongly hydrophobic poly(perfluoropropylene oxide)(denoted as C),13-15,19which is successfully used to study the famous experimental work of Lodge and co-workers.11In this work,we adopt the same DPD repulsion parameters with the references13-15,19as shown in Table 2 to best compare our results with those from simulations and experiments.The water molecule(W)is modeled as a single DPD bead,and the triblock copolymers AxByCzand diblock copolymer AmBnare modeled by connected DPD beads.The simulations are performed in a cubic box of size 40rc×40rc×40 rcfor the blend of linear triblock copolymers and diblock copolymers.The total volume fraction of the blend of triblock copolymers and diblock copolymers is 0.10 to guarantee the dilute aqueous solution.It should be noted that linear triblock copolymers and diblock copolymers possess the same volume fraction but different block length.The initial conformations of the block copolymers are generated randomly by the random number.Using Eq.(6),for a given noise amplitude,we put KBT=1.27Periodic boundary conditions are applied.The time step Δt is taken as 0.05,6×105DPD time steps are carried out to attain equilibration for each system,which is long enough compared with literature.19

3 Results and discussion

The blend of linear triblock copolymer AxByCzand diblock copolymer AmBnwith different block chain lengths can selfassemble into various morphologies which possess different potential applications.To illustrate the influence by only changing block chain length of block copolymer,we study the selfassembled structures from the blend of four different linear triblock copolymers AxByCz(A4B4C4,A2B4C6,A5B2C5,and A2B2C8)and three different linear diblock copolymers AmBn(A6B6,A3B9,and A9B3)using DPD simulations.The obtained morphologies of multicompartment micelles are mainly controlled by free energy change and the competitive interactions between differentbead-pairs.In solution,hydrophilic block B should strongly protect hydrophobic block C from contacting to water.In the meantime,the weakly hydrophobic block A would like to protect hydrophobic block C and be protected by hydrophilic block B.The different self-assembled morphologies are obtained by blending different linear triblock copolymers and diblock copolymers.It clearly reflects the sensitive dependence of the multicompartment micelle structure on the block chain length of block copolymer.

Table 2 DPD bead-bead interaction parameter αij

For A4B4C4triblock copolymer,when it is blended with A6B6diblock copolymer,the morphology of the self-assembled multicompartment micelle is“worm-like”micelle.The block A and block C form separated cores,and then are surrounded by the block B.Due to the fraction of block A larger than block C in the blend of block copolymer,the aggregated area of block A is larger than that of block C(Fig.2(a,d)).For A4B4C4triblock copolymer blended with A3B9and A9B3diblock copolymers respectively,the molar ratio of block A and block B is changed from 7:13 to 13:7.These result in that the morphology of self-assembled multicompartment micelle is changed into the hamburger micelle connected with worm-like micelle(Fig.2(b,c,e,f)).If the chain length of block A is shorter and the chain length of block C is longer in the triblock copolymer,the structures of multicompartment micelles self-assembled from this triblock copolymer blended with the same diblock copolymer are totally different.

For A2B4C6triblock copolymer,blended with A6B6,A3B9,and A9B3diblock copolymers the structures of self-assembly are“hamburger”micelle,“sphere on sphere”micelle,and“wormlike”micelle,respectively,shown in Fig.2(g,h,i).The increased ratio of strongly hydrophiphilic block B makes the selfassembled morphologies become more spherical shape.If the ratio of block B in the triblock copolymer is decreased,the structures of multicompartment micelles are also different.

Fig.2 Morphologies of the multicompartment micelles from the blends(a)-(f)in Table 1

For triblock copolymer A5B2C5,in which block A and block C have the same chain length,and the ratio of block B is de-creased,the morphologies of multicompartment micelles are“worm-like and hamburger”micelle(blended with A6B6),small hamburger micelle(blended with A3B9),and“wormlike”micelle(blended withA9B3),shown in Fig.3(a-c),respectively.

After changing the ratio of blockAand block C in the triblock copolymer,for the blend of A2B2C8triblock copolymer and A6B6diblock copolymer,they self-assemble into the“hamburger”micelle as shown in Fig.3(g).Furthermore,the“sphere on sphere”micelle and“core-shell-corona”micelle are obtained from the blend of A2B2C8triblock copolymer and A3B9diblock copolymer,and the blend of A2B2C8triblock copolymer and A9B3diblock copolymer,respectively.The micelles prefer the maximum(minimum)contacting between B(C)and water,meanwhile to avoid the free energy penalty due to drastic interface curvature change.19

The density profiles(ρ)of the A,B,and C components in different directions are calculated in order to better describe the morphologies of the multicompartment micelles(Fig.4).For example,from Fig.4a which shows the density profiles along X direction,we find alternating maxima of components A,B,and C,which reflect the layer by layer structure(Fig.2(a,d))self-assembled from the blend of A4B4C4triblock copolymer and A6B6diblock copolymer.This alternating maxima of components A,B,and C are also found in the Z direction as shown in Fig.4b,which corresponds the structure of multicompartment micelles shown in Fig.2(b,e).It should be noted that the green line of block C and red line of block A have the opposite direction,which represents the different cores of the multicompartment micelles formed from different blocks.Similar line shapes are also found in Fig.4d,which correspond to the morphologies of“worm-like”micelles self-assembled from blend ofA5B2C5andA6B6block copolymers.

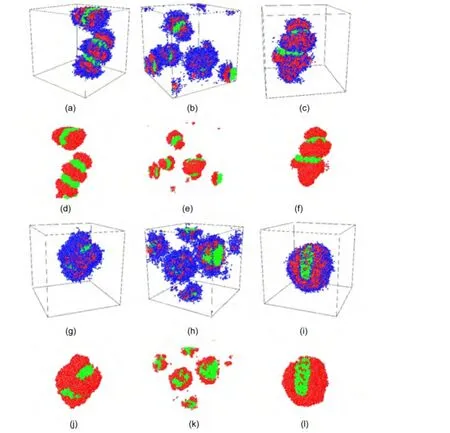
Fig.3 Morphologies of the multicompartment micelles from the blends(g)-(l)in Table 1

Fig.4 Density profiles in X,Y,and Z directions

Fig.5 Radial distribution functions of multicompartment micelles from blends(a)-(f)in Table 1

Fig.6 Radial distribution function of multicompartment micelles from blends(g)-(l)in Table 1

Furthermore,from Fig.4c,we can find an enrichment region of block C with green line,which corresponds to the core region of the“hamburger”micelle structure shown in Fig.2(g)formed from the blend of A2B4C6and A6B6block copolymers.Similar line shapes are also found in Fig.4f,which are from the morphology of“hamburger”micelle shown in Fig.3(g).From Fig.4e,the enrichment region of block A with red line in the Z direction is very large,which shows the large aggregated area of block A occupying the blend of A5B2C5and A9B3block copolymers.

In order to further analyze the structures of the multicompartment micelles,the pair distribution function g(r)is also calculated.The function gives the probability of finding a pair of particles with a distance r apart,which is formally defined by30

where N is the number of particles and V is the volume of the simulation box.

g(r)between A,B,and C components of blend of triblock copolymers AxByCzand diblock copolymers AmBnare calculated and shown in Fig.5 and Fig.6,respectively.Fig.5a corresponds to g(r)of the multicompartment micelle formed by the blend of triblock copolymer A4B4C4and diblock copolymer A6B6.gCC(r)possesses the highest peak,which can be attributed to the compact aggregation formed by C block.Furthermore,the order of rCC

Moreover,although the second peak is flat,there are apparently two peaks for gAA(r),which reflect the typical layered structures as shown in Fig.5(b,f).From Fig.5d and Fig.6d,we can find that the aggregate C is near toAand far from B.Therefore,a“hamburger”micelle structure with block C as the core shown in Fig.2(g)and Fig.3(g)can be deduced.In Fig.6e,the position at which g(r)corresponds to the maximum is the order of rBB

4 Conclusions

In this work,the sensitive influence of the blend of triblock copolymers AxByCzand diblock copolymers AmBnon the morphology diversity of the multicomparment micelles is investigated using dissipative particle dynamics.Through changing the block chain length of triblock copolymers and diblock co-polymers,the blend of different triblock copolymers and diblock copolymers could self-assemble many various multicompartment micelles which are observed in our simulations.Furthermore,the structures of the multicompartment micelles are analyzed by the calculated density profiles and the pair distribution function.The results in primary complement for the experiments with the possibilities on the preparation of the multicompartment micelles by blending different triblock copolymers and diblock copolymers.

(1) Bates,F.S.;Hillmyer,M.A.;Lodge,T.P.;Bates,C.M.;Delaney,K.T.;Fredrickson,G.H.Science 2012,336,434.doi:10.1126/science.1215368

(2)Weiss,P.S.ACS Nano 2008,2,1085.doi:10.1021/nn800314e

(3) Li,Z.B.;Hillmyer,M.A.;Lodge,T.P.Macromolecules 2006,39,765.doi:10.1021/ma052199b

(4) Kubowicz,S.;Baussard,J.F.;Lutz,J.F.;Thünemann,A.F.;Berlepsch,H.V.;Laschewsky,A.Angew.Chem.Int.Edit.2005,44,5262.

(5)Thünemann,A.F.;Kubowicz,S.;Berlepsch,H.V.;Möhwald,H.Langmuir 2006,22,2506.doi:10.1021/la0533720

(6) Kotzev,A.;Laschewsky,A.;Adriaensens,P.;Gelan,J.Macromolecules 2002,35,1091.doi:10.1021/ma011047n

(7) Li,Z.B.;Hillmyer,M.A.;Lodge,T.P.Langmuir 2006,22,9409.doi:10.1021/la0620051

(8) Synatschke,C.V.;Löbling,T.I.;Förtsch,M.;Hanisch,A.;Schacher,F.H.;Müller,A.H.E.Macromolecules 2013,46,6466.doi:10.1021/ma400934n

(9) Hanisch,A.;Gröschel,A.H.;Förtsch,M.;Löbling,T.I.;Schacher,F.H.;Müller,A.H.E.Polymer 2013,54,4528.doi:10.1016/j.polymer.2013.05.071

(10) Hanisch,A.;Gröschel,A.H.;Förtsch,M.;Drechsler,M.;Jinnai,H.;Ruhland,T.M.;Schacher,F.H.;Müller,A.H.E.ACS Nano 2013,7,4030.doi:10.1021/nn400031u

(11)Li,Z.B.;Kesselman,E.;Talmon,Y.;Hillmyer,M.A.;Lodge,T.P.Science 2004,306,98.doi:10.1126/science.1103350

(12)Lodge,T.P.;Rasdal,A.;Li,Z.B.;Hillmyer,M.A.J.Am.Chem.Soc.2005,127,17608.doi:10.1021/ja056841t

(13) Zhong,C.;Liu,D.Macromol.Theory Simul.2007,16,141.

(14) Liu,D.;Zhong,C.Polymer 2008,49,1407.doi:10.1016/j.polymer.2008.01.034

(15) Xia,J.;Liu,D.;Zhong,C.Phys.Chem.Chem.Phys.2007,9,5267.doi:10.1039/b705359b

(16) Huang,C.I.;Fang,H.K.;Lin,C.H.Phys.Rev.E 2008,77,031804.doi:10.1103/PhysRevE.77.031804

(17) Huang,C.I.;Chiou,Y.J.;Lan,Y.K.Polymer 2007,48,877.doi:10.1016/j.polymer.2006.12.017

(18) Chou,S.H.;Tsao,H.K.J.Chem.Phys.2006,125,194903.

(19) Zhao,Y.;Liu,Y.T.;Lu,Z.Y.;Sun,C.C.Polymer 2008,49,4899.doi:10.1016/j.polymer.2008.08.063

(20) Zhao,Y.;You,L.Y.;Lu,Z.Y.;Sun,C.C.Polymer 2009,50,5333.doi:10.1016/j.polymer.2009.09.014

(21) Xin,J.;Liu,D.;Zhong,C.J.Phys.Chem.B 2009,113,9364.doi:10.1021/jp902300g

(22) Chen,H.;Ruckenstein,E.Soft Matter 2012,8,1327.doi:10.1039/c2sm06968g

(23) Chang,H.Y.;Lin,Y.L.;Sheng,Y.J.Macromolecules 2012,45,4778.doi:10.1021/ma3007366

(24)Han,M.;Hong,M.;Sim,E.J.Chem.Phys.2011,134,204901.doi:10.1063/1.3586804

(25) Jiang,T.;Wang,L.;Lin,S.;Lin,J.;Li,Y.Langmuir 2011,27,6440.doi:10.1021/la201080z

(26) Hoogerbrugge,P.J.;Koelman,J.M.V.A.Europhys.Lett.1992,19,155.doi:10.1209/0295-5075/19/3/001

(27) Groot,R.D.;Warren,P.B.J.Chem.Phys.1997,107,4423.doi:10.1063/1.474784

(28) Español,P.;Warren,P.W.Europhys.Lett.1995,30,191.doi:10.1209/0295-5075/30/4/001

(29) Groot,R.D.;Madden,T.J.J.Chem.Phys.1998,108,8713.doi:10.1063/1.476300

(30)Allen,M.P.;Tildesley,D.J.Computer Simulation of Liquids;Clarendon Press:Oxford,1987.