数学思想方法有意义学习策略

任淑香

高中数学教学不可缺失了数学思想方法的渗透，思想方法是对数学知识、技能在更高层次上的抽象，是学生能够顺利完成学习目标的关键.所谓有意义的学习即以学生为主体，自主探究并将数学思想方法内化到自己认知结构的学习过程.本文就如何实现数学思想方法的有意义学习谈几点笔者的看法，望能有助于高中数学教学实践效果的提升.

一、数学思想方法及其特征

1.什么是数学思想方法

中学数学教学理论表明，所谓“数学思想方法”指的是数学思想与数学方法的统称.前者指的是前人在社会生产、实践及数学研究过程中，对数学知识和方法形成的理性的、具有规律性的看法和成式化的认识；后者指的是研究某一个或某一类数学对象的活动过程中涉及的研究途径、研究程序、研究手段，等等，具有过程性、层次性、可操作性等特点.

2.数学思想方法有哪些特征

（1）导向性，数学思想方法是数学思维的核心策略，是人们研究数学和解决数学问题的指导思想，具有导向性，除此之外，其导向性还表现在思想方法是数学家建立数学体系，催生数学学科发展之根源.

（2）统摄性，这一特征可以从如下两个方面进行概括：其一数学思想方法优化数学知识结构，其二数学思想方法发展数学认知结构.

（3）概括性，数学知识、概念具有概括性，思想方法更具概括性，而且概括性程度的高低不同，数学思想方法所处的层次也不一样.能够解决的数学问题和对问题本质的理解也不一样，概括化程度越高，抽象度越大，能够揭示的数学对象其本质越深刻，对数学问题的理解和解释越透彻.

（4）迁移性，运用数学思想方法解释、理解和解决数学问题的过程实际上就是思想方法迁移的过程，数学思想方法的迁移性主要集中在数学学科内部，数学思想方法作为较高层次的概括，是数学知识的基础与源泉，通过数学思想方法的迁移，数学学科各部分知识、规律之间有效的联结，构建成理论化的学科体系.

二、数学思想方法教学目标的设置

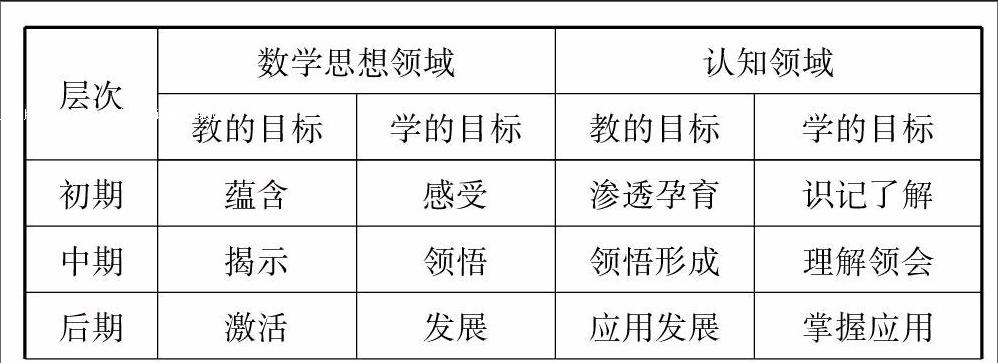
学生数学思想方法的形成不是一蹴而就的，必然有一个从模糊到清晰的过程，从理解到应用的较长发展过程，笔者将数学思想方法教学目标进行了设置如下表.

如何实现教学目标呢？结合平时的教学实践，笔者总结为如下几点.

1.在数学知识学习和发生的过程中，进行数学思想方法的渗透.

2.在课堂教学，具有思维活动的过程中，调动学生的思维，揭示数学思想方法.

3.设置具体的问题，引导学生在思考与探索解决问题的方法时，激活学生头脑中的数学思想方法.

4.在复习阶段或是课堂知识总结和归纳阶段，自主概括数学思想方法.

三、教学案例——学会分类讨论方法

通常情况来说，分类讨论方法在数学问题解决过程中经常会用到，在使用时要注意如下几个方面：首先，对具体的数学问题进行分析，通过分析确定该问题是否需要采用分类讨论方法.从实践经验来看，如果数学问题中存在变化的、不确定的影响因素或动态因素，或是问题不便统一处理时，需要分类讨论；其次，对数学问题或数学对象进行分析，找出具体的破坏问题处理统一性的原因或是特殊对象，由此确定分类的界值、准则，实施分类确保在每一类数学对象中能够统一操作解决问题；然后，按照所分类别，逐类进行问题的解决，获得结果，这个过程是运用数学概念、思想方法对每一类实施数学操作或运算的过程；最后，将各类结果进行归纳与综合，得到结论.

例如，已知y=|2x+6|+|x-1|-4|x+1|，求y的最大值.由于函数表达式中有“绝对值”的存在，导致数学问题不便于操作.首先要将“绝对值”去掉，这时从绝对值的意义出发，分类讨论的需要就产生了：要考虑每个绝对值号内的代数式取正、负的不同情况.运用“零点分段法”：从3个绝对值各自的零点出发进行思考，函数有3个分界零点：“-3，1，-1”.如此，定义域被这三个分界零点分成4个区间，由于各个区间内的绝对值符号内，各个表达式都有确定的正、负.这样，可以同时将各个区间内的绝对值符号去掉，分别求出4个区间段上的最大值，最后比较可以得出最大值.