航天器共振轨道特性研究

史格非, 方群

(西北工业大学 航天飞行动力学技术国家重点实验室, 陕西 西安 710072)

0 引言

在空间机动过程中,发动机推力大小有限,推进并非瞬间完成,特别是对于容许过载比较小的航天器进行轨道机动时,冲量假设不再成立,必须研究连续推力轨道机动。对于连续推力机动轨道的描述有很多[1],本文所研究的共振轨道就是一种新型的连续推力轨道。

共振是自然界的一种普遍现象,航天器在连续推力作用下的运动在参数平面内可以视为一种受迫振动,也会发生共振现象。因此,可以利用共振原理来研究航天器的运动,称这样一类非开普勒轨道为共振轨道(值得注意的是,这里的共振轨道与天体力学中定义的共振轨道有本质的不同[2])。航天器的共振轨道实质上是一种建立在新型坐标系下的非开普勒轨道,它是一种可以应用于轨道机动的过渡轨道。航天器共振轨道理论提出时间不长,国内外在这方面的研究还很少。

本文是在文献[3]提出的共振轨道理论的基础上深入研究共振轨道的轨道特性。通过对共振轨道在典型任务中的应用与传统轨道机动模式进行仿真对比分析,阐述了单段共振轨道在航天器轨道机动中应用的优势与不足。

1 航天器共振轨道模型的建立

1.1 共振轨道模型

航天器在平方反比中心引力和推力作用下的平面运动方程为:

(1)

引入新的时间尺度s(广义偏近点角),它和物理时间t的关系为[3]:

(2)

式中,E为航天器单位质量具有能量的负数。

由Levi-Civita变换[4]可得:

r=L(u)u

(3)

在此基础上引入准推力加速度[3]:

q=Mp

(4)

准推力可以视为对推力进行坐标变换的一种推广。准推力与航天器质量的比称为准推力加速度。其中:

(5)

利用式(2)～式(4)可以将式(1)转化为线性方程:

该方程即为平面Y-C方程[3]。

假设准推力加速度为简谐激励,即准推力加速度具有如下形式:

(6)

式中,A1,A2为幅值;ω为准推力加速度的角频率;φ1,φ2为初始相位。令:

(7)

则式(6)可以写为:

q(s)=acos(ωs)+bsin(ωs)

(8)

将式(8)代入平面Y-C方程(ω=1/2),解得平面共振轨道的轨道方程为:

(9)

1.2 物理坐标系与参数坐标系的相互转换

物理坐标系即地心坐标系,其参数为通常使用的位置、速度矢量。参数坐标系是一个通过对物理坐标系参数进行L-C变换而得到的新的坐标系,其参数皆为无量纲参数。

文献[3]中的L-C变换为数学上的变换,没有考虑计算机仿真应用。为了便于计算机仿真,避免仿真过程中会因出现奇异点而引起仿真失败,本文将物理平面与参数平面上的点用参数的形式表示:

x=rcosθ,y=rsinθ

根据L-C变换的定义并结合几何意义,可以得到一个物理平面上的点所对应的两个参数平面上的点:

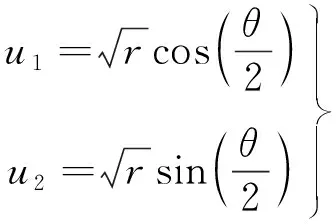
(10)

在得到物理-参数坐标的转换后即可以利用L-C速度转换式[4]:

(11)

得到对应点处的速度矢量。

1.3 参数描述

由于共振轨道模型是建立在参数坐标系下的,因此应用共振轨道时始终存在轨道参数在参数坐标系和物理坐标系之间的转化。物理坐标系下的位置矢量可以表示为:

(12)

将式(9)代入上式,可以得到x和y关于s的表达式,带入式(11)可以得到速度矢量关于s的表达式。从而得到以广义偏近点角s为自变量的轨道与速度(x(s),y(s),vx(s),vy(s))方程。

2 利用共振轨道进行轨道机动的仿真分析

2.1 仿真模型的建立

将能量的表达式改写为:

(13)

利用式(5)和式(13)可以求出任意s值所对应的M和E。由式(8)则可以得到任意s下的准推力矢量。利用式(2)和式(4)可以将参数坐标系下的时间尺度(广义偏近点角)和准推力转化为其在物理平面上所对应的时间和推力。利用式(12)即可得到物理坐标系下任意时刻的位置矢量。利用式(11)可以得到物理坐标系下任意时刻的速度矢量。

2.2 仿真算例

2.2.1 仿真条件

航天器的初始运行轨道为8 000～16 000 km的椭圆轨道;目标轨道为7 000～21 000 km的椭圆轨道;目标轨道相对于航天器初始运行轨道的拱线间夹角为25°(逆时针)。

通过单段共振轨道将初始轨道上的航天器机动到目标轨道上从而实现变轨。由于无法确定最省燃料的轨道初始位置和到达位置,因而采用穷举法对初、末位置和时间尺度(广义偏近点角)进行筛选和分析。将航天器初始运行轨道和目标轨道分别等分为36份从而得到36×36组出发/到达点,对每一组出发/到达点之间转移所经过的s进行穷举和筛选,得到每一组点的最佳时间尺度。在得到每一组的最优转移轨道后,对36×36条轨道进行横向比较,选出最省燃料的轨道并进行分析。

2.2.2 仿真结果及分析

仿真得到的燃料最省机动轨道参数结果为:航天器出发位置(x0,y0)=(6 509,5 462)km,航天器变轨到达位置(xf,yf)=(-14 005,-14 005) km,变轨速度增量ΔV=989.212 1 m/s,变轨飞行时间Δt=11 195 s,参数时间尺度sf=3.752 rad。航天器初始、目标及机动轨道如图1所示。

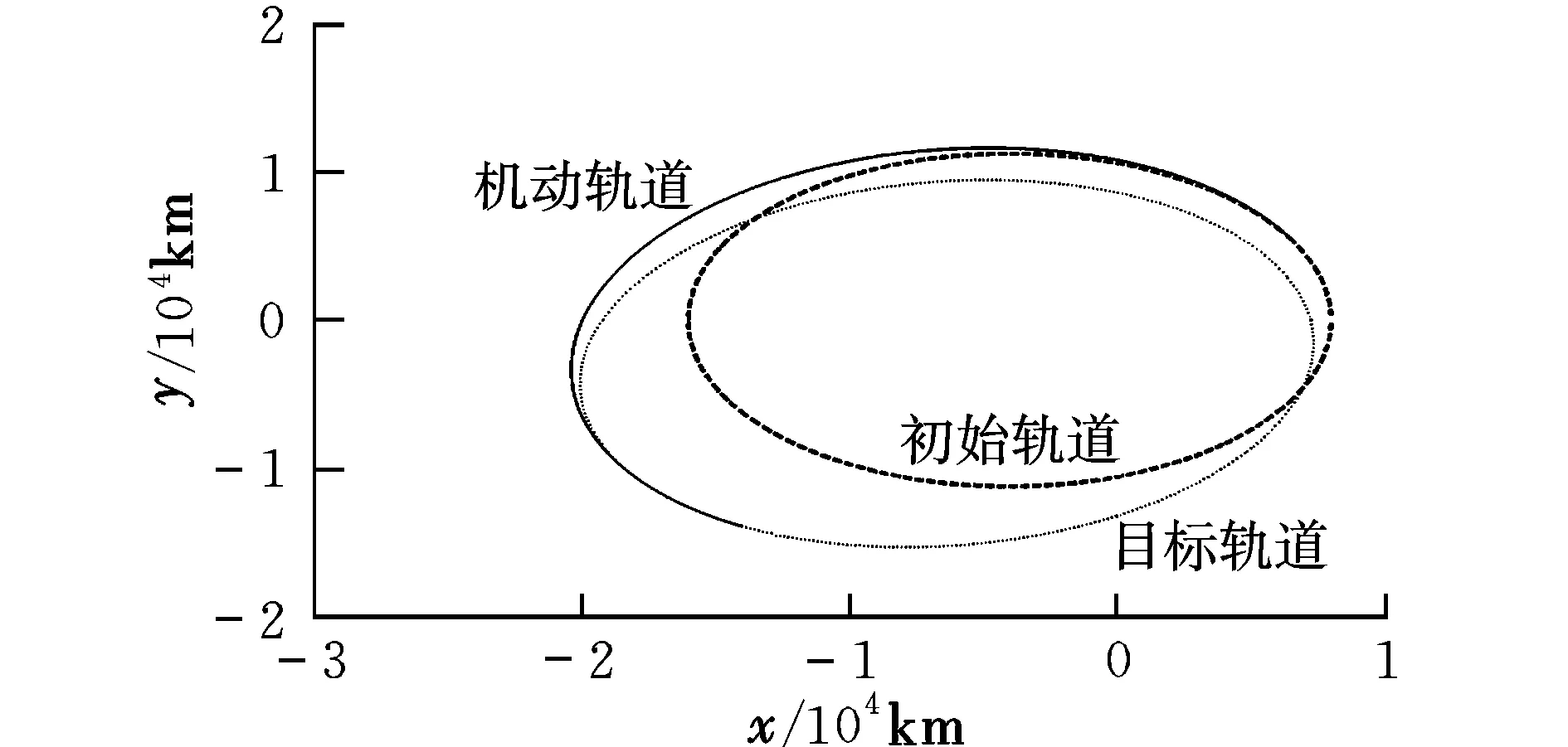
图1 共振机动轨道示意图Fig.1 Resonance transfer orbit

在本文的算例中,采用传统的轨道机动策略,即在两条轨道交点处通过施加脉冲进行变轨所需的速度增量为1 504 m/s[5],而利用共振轨道进行机动变轨所需的速度增量为989.211 2 m/s,这个数值大约为传统单脉冲法的2/3。可见相比于单脉冲的轨道转移方法,共振机动轨道是节省燃料的。因而在不考虑机动时间约束的情况下,利用共振机动轨道进行有交点轨道的变轨要优于单脉冲变轨。

本算例的推力曲线如图2所示。由图2可以看出,在整个机动飞行阶段,推力峰值没有超过0.35 N,即任意时刻的速度增量均在0.05～0.35 N之间,远小于应用Lambert转移时所需的最小速度增量(最小脉冲),这意味着应用共振轨道进行轨道机动的航天器不必使用大推力火箭发动机,即可产生的推力大小不再成为一种主要限制。

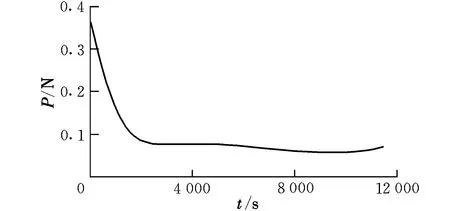
图2 共振轨道推力曲线Fig.2 Resonance orbit thrust curve

在消耗相同时间的情况下,利用双脉冲,通过Lambert转移进行变轨得到的结果为:转移时间Δt=11 195 s;第一次脉冲的速度增量ΔV1=659.7 m/s;第二次脉冲的速度增量ΔV2=222.6 m/s,总的速度增量ΔV=882.3 m/s。

将共振机动轨道与Lambert轨道进行对比可见,在时间相同的条件下,应用共振机动轨道进行变轨所消耗的燃料要略多于Lambert轨道。

3 共振轨道周期性和时间尺度分析

3.1 共振轨道周期特性分析

由共振轨道方程式(8)可知,在无推力的情况下，共振轨道是一种周期轨道。在有推力的情况下(以上文的算例为例),尽管共振轨道不是周期轨道,但也呈现出一种准周期性质。图3表示对于同一组初始和到达参数,等效速度增量随参数时间尺度变化量sf(广义偏近点角改变量)的改变而发生的变化。这种变化带有明显的周期性。通过分析轨道参数与等效速度增量可知,等效速度增量的下峰值随广义偏近点角sf变化量的变化而有规律的出现,大约每4π rad出现一次。

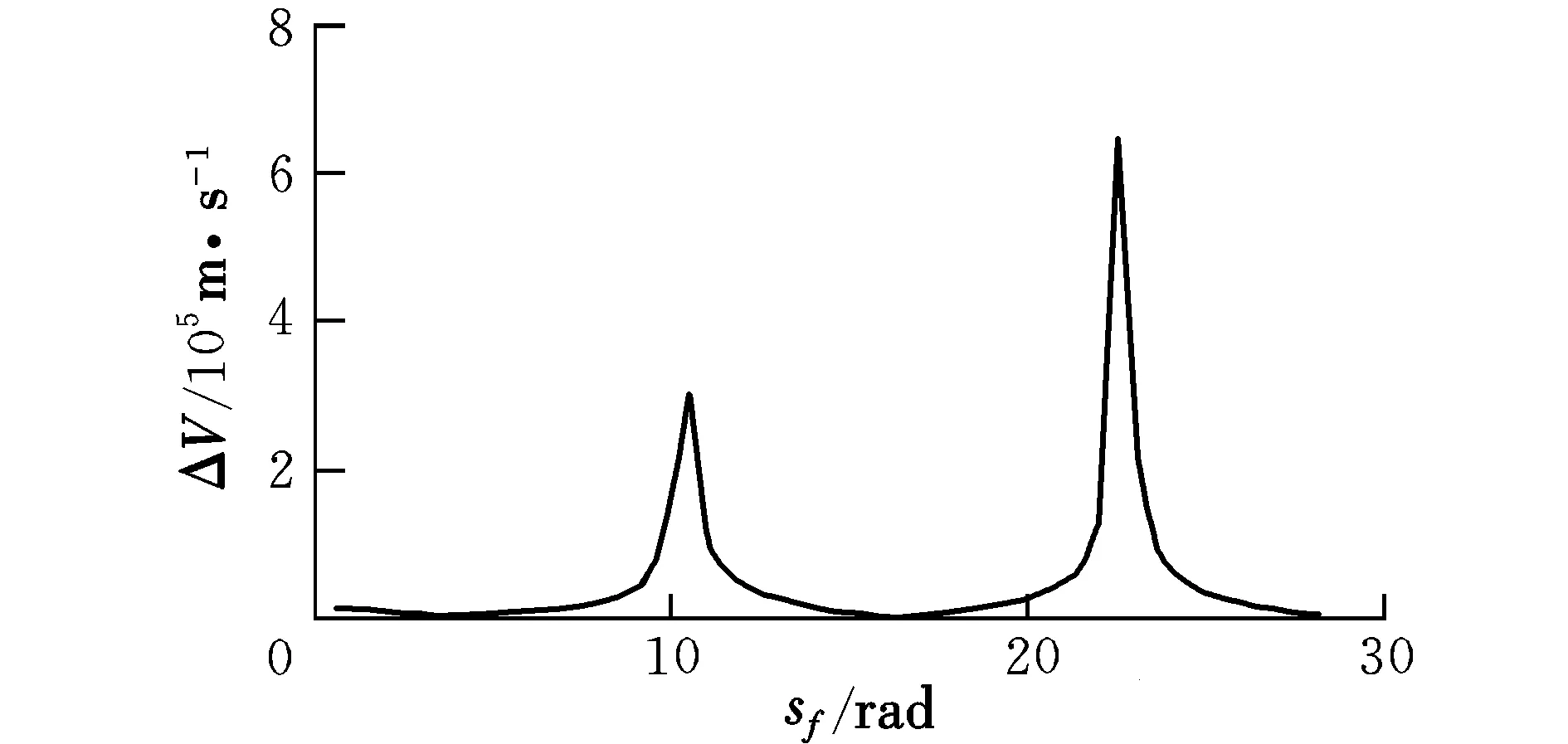
图3 等效速度增量随sf的变化曲线Fig.3 Changing of equivalent velocity with sf

由物理学知识可知:物体振动周期为2π/f。由于本文所建立的共振轨道方程其频率为0.5,因此在理论上,共振轨道周期应该为4π。可见下峰值周期的出现是符合共振轨道的物理性质的。

3.2 共振轨道参数时间尺度特性分析

对于推力为0的共振轨道方程,共振轨道形式的线性开普勒轨道方程为:

(14)

在开普勒共振轨道方程下,s即对应为物理平面内航天器的偏近点角。在非开普勒轨道方程下,根据式(10),由于推力不再为0,因此a1,b1,a2,b2不再都等于0。共振轨道不再是式(12)所表示的简谐振动轨道,sf与Δθ的严格对应关系也不再存在。

图4中的曲线表示2.2节的仿真算例中，各组出发和到达参数所对应的最小等效速度增量所对应的sf值与物理平面内航天器所转过的实际偏近点角的比值。图中，横坐标n为仿真结果序号。

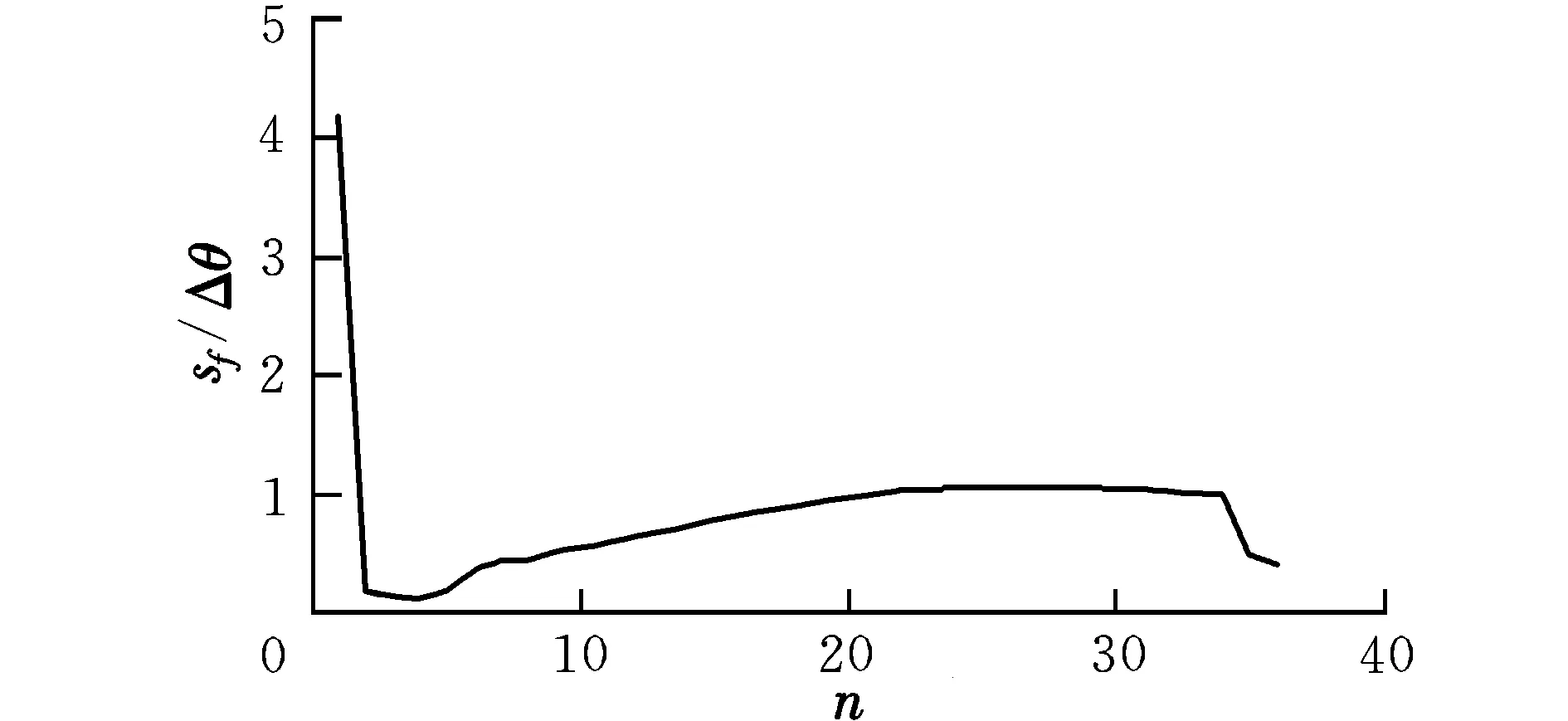
图4 sf/Δθ曲线Fig.4 sf/Δθ curve

由图4可知,sf/Δθ≠1,这说明在由式(9)所描述的有推力共振轨道中,广义偏近点角s的变化量与物理平面上的偏近点角改变量没有固定的对应关系。这意味着对于有推力的共振轨道,无法通过研究物理平面偏近点角的改变量来得到任务所需的最佳广义偏近点角改变量sf。因此对最适合的航天器始轨道变轨和目标轨道到达点以及相应的sf的选择目前只能应用穷举法来实现。

4 结束语

本文针对频率为0.5的典型共振轨道,从模型和参数描述以及转换等方面进行了分析和补充,提出了共振轨道物理平面方程的直接参数描述方法。通过对共振轨道在典型任务中的应用与传统轨道机动模式进行仿真对比分析,阐述了单段共振轨道在航天器轨道机动中应用的优势与不足。同时,通过仿真计算对共振轨道周期特性进行了研究。

研究结果表明，在不考虑飞行时间约束的情况下,应用单段共振轨道作为转移轨道要比传统转移轨道更节省燃料;在时间相同的情况下,共振转移轨道消耗的燃料比Lambert轨道略多,但对发动机的推力要求很低;对于共振轨道的周期特性,广义偏近点角s的变化量与物理平面上的偏近点角改变量没有固定的对应关系。

参考文献：

[1] McInnes C R.Solar sail mission applications for non-Keplerian orbits [J].Acta Astronautica,1999,45(4):567-575.

[2] 万晓生,黄天依.冥王星轨道运动中的共振[J].紫金山天文台台刊,2000,19(2):80-84.

[3] 陈记争.航天器非开普勒轨道研究[D].西安:西北工业大学,2010.

[4] 易照华,孙义燧. 摄动理论[M].第一版.北京:北京科学出版社,1981:52-76.

[5] Howard D Curtis.轨道力学[M].第一版.周建华,徐波,冯全胜,译.北京:科学出版社,2009:226-229.