改进鱼群算法在飞机下滑配平中的应用

陶杨, 韩维, 宋伟健

(1.海军航空工程学院 飞行器工程系, 山东 烟台 264001;2.海军航空工程学院 科研部, 山东 烟台 264001)

0 引言

飞机的运动状态是由一系列非线性微分方程来描述的。在以往的配平计算中,多是令飞行状态下状态参数的时间导数为零,从而将非线性微分方程组简化为一组非线性代数方程组,通过Newton迭代法[1]、梯度下降法[2]等数值方法来求解,但采用这类方法存在一个问题,即对初值的选取具有很大的依赖性,只有当初值与平衡点很接近时才能较快收敛,否则会造成迭代步数的增加甚至出现不能收敛的情况。

为了解决该问题,近年来有学者提出采用数值优化的方法,首先构建一个代价函数,用各种智能寻优算法,如遗传算法[3-5]、模拟退火算法[6]等,通过求得代价函数的极值,从而确定飞行的平衡状态,但由于算法的局限性,采用单一算法存在易陷入局部最优解的缺点。

本文采取了一种新型自适应变异算子的人工鱼群算法来求解定常下滑过程中的飞机平衡状态。该算法在求解时既能保持高效搜索效率,同时也能避免陷入局部最优的情况发生。

1 飞机下滑动力学模型及代价函数的选取

飞机保持一定的下滑角沿下滑道匀速运动,在该过程中,飞机为定常飞行状态,采用英美坐标系,此时的动力学模型为:

m(dV/dt)=Tcos(σ+α)cosβ-D-mgsinγ

mVcosγ(dχ/dt)=T[-cosμsinβcos(σ+α)+

sinμsin(σ+α)]+

Ysinμ+Ccosμ

mV(dγ/dt)=T[sinμsinβcos(σ+α)+

cosμsin(σ+α)]+Ycosμ-

Csinμ-mgcosγ

dq/dt= [-(Ix-Iz)pr-Izx(p2-r2)+

M+Te]/Iy

此外,需补充欧拉角的角度关系使模型封闭。

sinα={cosγ[cosφsinθcos(ψ-χ)+

sinφsin(ψ-χ)]-sinγcosφcosθ}/cosβ

sinβ=cosγ[sinφsinθcos(ψ-χ)-

cosφsin(ψ-χ)]-sinγsinφcosθ

sinμ={sinγ[sinφsinθcos(ψ-χ)-

cosφsin(ψ-χ)]+cosγsinφcosθ}/cosβ

这里,取代价函数为：

2 配平算法

2.1 自适应变异算子人工鱼群算法

人工鱼群算法[7]是基于模拟鱼类随机游动、追尾、聚群、觅食等行为提出的一类群体智能优化算法。该算法思想源于自然界水域中的鱼往往能自行或者尾随其他鱼找到食物,因而一般食物多的地方也存在较多鱼的这一自然现象。其具有对初值与参数选择不敏感、简单易实现和使用灵活等特点,但随着人们对该算法应用领域的不断拓展,一些缺点也显现了出来:参数采用固定值的这种做法在一定程度上扩大寻优范围的同时也会减缓收敛速度;拥有很强的正反馈性,寻优过程中能很快找到较优解,但与此同时也使得种群的多样性迅速丧失,易造成过早收敛,陷入局部最优,从而无法得到全局最优解。考虑到这些缺点与不足,本文提出了一种新型自适应变异算子的人工鱼群算法。

2.1.1 自适应步长和视野

标准鱼群算法采用了固定视野和步长,使得在优化过程的初期具有较快的收敛品质,但在后期往往收敛较慢或者很难得到要求的精度。为了修正这一不足,这里采用如下解决方案:

(1)每次迭代计算出每条鱼与鱼群其他个体之间的距离,并将该距离的平均值作为其视野vvis;

(2)给出一个步长系数a,把avvis作为该鱼的步长s。

这样,可保证在算法初期鱼群比较分散时每条鱼都有较大的视野和步长,保证了寻优的全局性；而在后期，随着鱼群的聚集，每条鱼的视野和步长也随之减小,可保证后期的收敛速度和精度。

2.1.2 感知作用

依据一些研究者对鱼群运动过程中个体间相互作用的研究,每条鱼自身都存在一个感知范围,根据个体间相对距离远近分为排斥行为、平行游动行为和吸引行为[8-11]。本文定义感知范围ddis,并将鱼群个体之间距离小于0.1ddis作为排斥距离rr,介于0.10ddis～0.25ddis之间作为平行游动距离rp,介于0.25ddis～0.50ddis之间作为吸引距离ra,大于0.50ddis则没有感知作用。对于鱼A而言,当鱼B处于rr区域,此时表现为排斥作用,A会向B的反方向运动;当B处于rp区域,此时B会保持与A之间的距离而与A平行游动,此时A与B相对静止;当B处于ra区域,此时表现为吸引作用,A会向B的方向运动,且假设鱼群个体间的吸引作用要大于排斥作用。

2.1.3 领导模式和吸引度

本文将动物群体中的领导模式和萤火虫算法的吸引度概念引入鱼群行为中。设某一时刻个体鱼A距离食物最近,其感知到的食物浓度为YA,此时A作为该鱼群的“领导者”吸引食物浓度较低区域C内的鱼向其运动,同时,C区域内的鱼又会成为食物浓度更低区域的鱼的“领导者”,并以此类推。

水域中个体鱼B能感知到的“领导者”A处的食物浓度YB=YAe-λdAB,其中,λ为衰减因子,dAB为A与B个体之间的距离。同样,A对B的吸引度为βB=βAe-λdAB。其中,鱼群“领导者”A的吸引度βA=1。随着距离的增加,领导模式和吸引度都会有所减弱。

2.1.4 鱼群变异

为克服上述现象,避免陷入局部最优解,本文在寻优过程解出的最优值在5次迭代中都未发生改变的情况下做以下处理:

(1)为防止最优鱼所处位置为局部最优,从而能有效摆脱局部极值的束缚,对最优鱼进行Gauss变异,即

Xbest-new=Xbest-old+Gauss(0,1)Xbest-old

式中,Gauss(0,1)为标准Gauss分布。

(2)为优化群体保持鱼群多样性,克服标准鱼群算法的早熟现象,对其他所有鱼进行遗传算法交叉和变异进化机制的操作,这样在提高收敛速度的同时保证了全局搜索能力。

2.1.5 鱼群行为描述

(1)鱼群初始化

鱼群的个体状态位置Xi={xi}(i=1,2,…,n),其中xi为待优化变量;目标函数Y=f(X)。

(2)觅食行为

个体鱼Xi以视野范围内随机选择另一个体鱼Xj,若Yje-λdij>Yi,则Xj会吸引Xi向其身边游动。

Xi|next=Xi+βiRs(Xj-Xi)/dij-

0.3(1-βi)Dr+0.7(1-βi)Da

若不满足该式,则个体鱼Xi再寻找视野内其他鱼;若个体鱼Xi在最大尝试次数中均未找到能满足条件的其他个体鱼,则个体鱼Xi执行随机行为。这里,定义R为(0,1)之间的随机数,Dr为该鱼与其他所有鱼之间的排斥作用引起的移动,Da为该鱼与其他所有鱼之间的吸引作用引起的移动。

R的加入使个体鱼Xi的移动方向确定但是大小不定,目的是通过引入随机因素以提高算法的鲁棒性。

(3)聚群行为

个体鱼Xi探索视野内的鱼群数目nf及中心位置Xc,如果Yce-λdic/nf>δYi(δ为拥挤度),表明鱼群中心有较多食物且不太拥挤,则:

Xi|next=Xi+αcRs(Xc-Xi)/dic-0.3(1-αc)Dr+

0.7(1-αc)Da

否则,执行觅食行为(这里人为规定鱼群中心的吸引度要弱于领导模式下的吸引度,αc=0.8βc)。

(4)追尾行为

个体鱼Xi探索视野内的鱼群数目nf及最优鱼位置Xb,如果Ybe-λdib/nf>δYi,表明当前最优鱼所处位置的食物浓度较大且周围不太拥挤,则:

Xi|next=Xi+βbRs(Xb-Xi)/dib-0.3(1-βb)Dr+

0.7(1-βb)Da

否则,执行觅食行为。

(5)随机行为

个体鱼Xi在其视野范围内随机移动一步,Xi|next=Xi+rvvis,其中r为区间(-1,1)的随机数。

2.2 算法流程

(1)计算初始化,定义计算所需的初始条件;

(2)通过2.1.5节的鱼群行为得出该次迭代下的代价函数最优值;

(3)对该最优函数值进行判断,若五次迭代中都未发生变化,则转到步骤(5),若不满足该条件则进入下一次循环迭代;

(4)判断是否达到最大循环迭代次数,若满足,则输出计算结果,不满足则返回步骤(2);

(5)对最优鱼进行Gauss变异,其余的鱼进行遗传交叉和变异,变异后的鱼群重复步骤(2)的操作。

3 飞机下滑运动的配平算例

根据下滑约束条件,偏航角ψ=0°，航迹方位角χ=0°,航迹角γ=-4°,给出飞行参数的大致搜索范围,并采用2.1节的算法初始条件对代价函数进行寻优。图1～图8为速度在40～80 m/s范围内飞机的下滑飞行参数配平值。

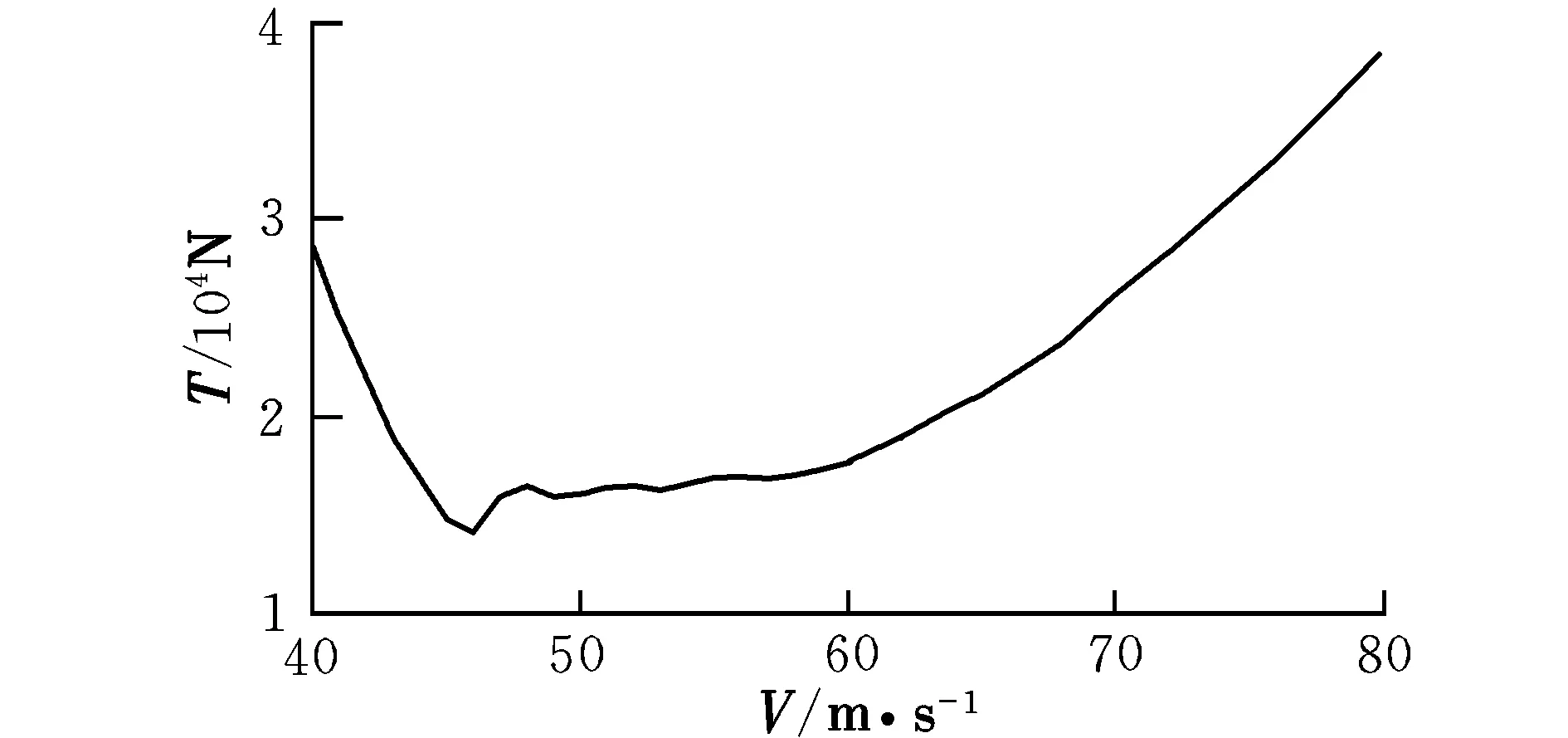
图1 配平推力随速度的变化曲线Fig.1 Trimming thrust with different velocities

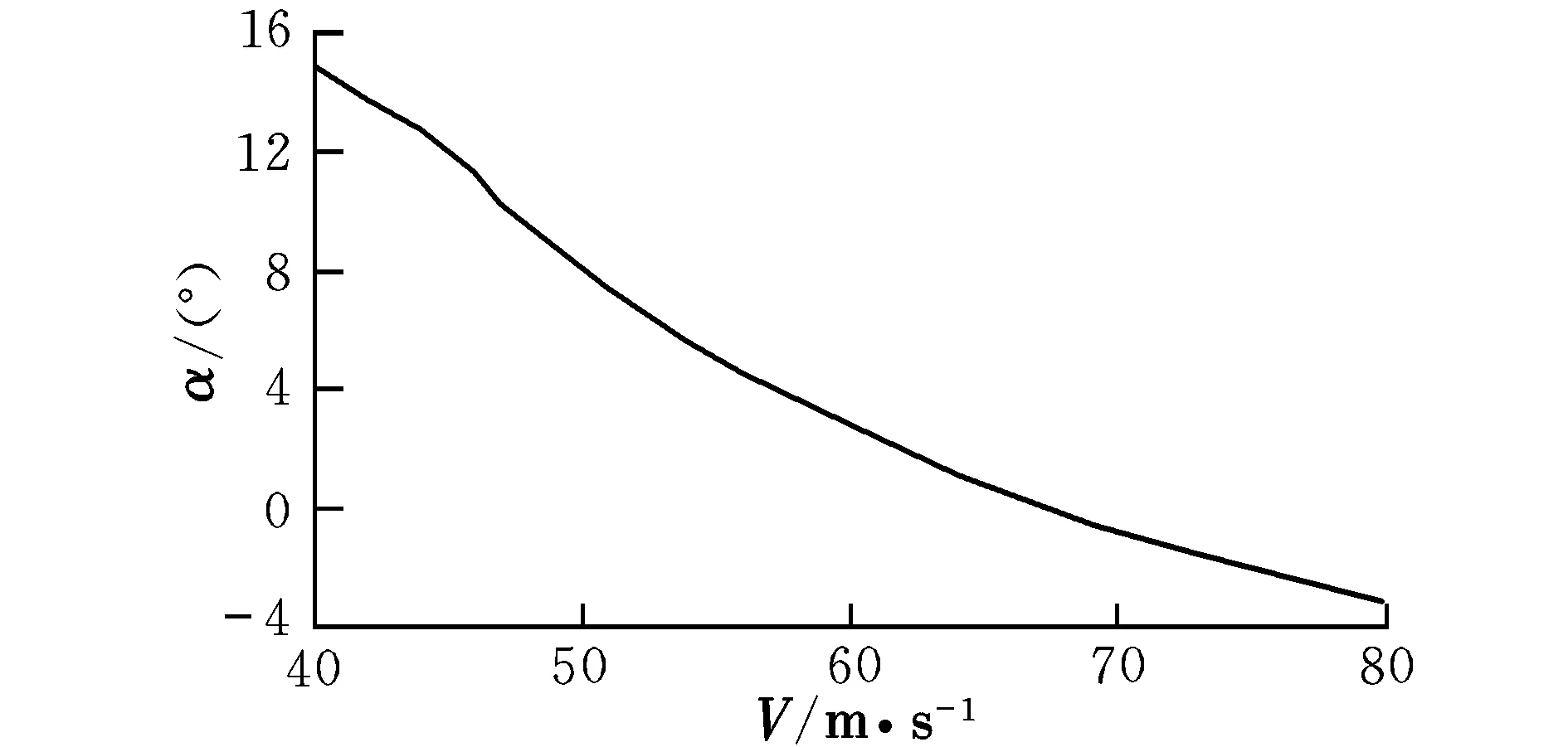
图2 配平迎角随速度的变化曲线Fig.2 Trimming attack angle with different velocities

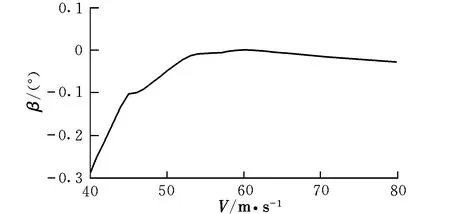
图3 配平侧滑角随速度的变化曲线Fig.3 Trimming sideslip angle with different velocities

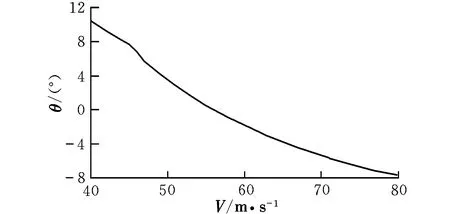
图4 配平俯仰角随速度的变化曲线Fig.4 Trimming pitch angle with different velocities

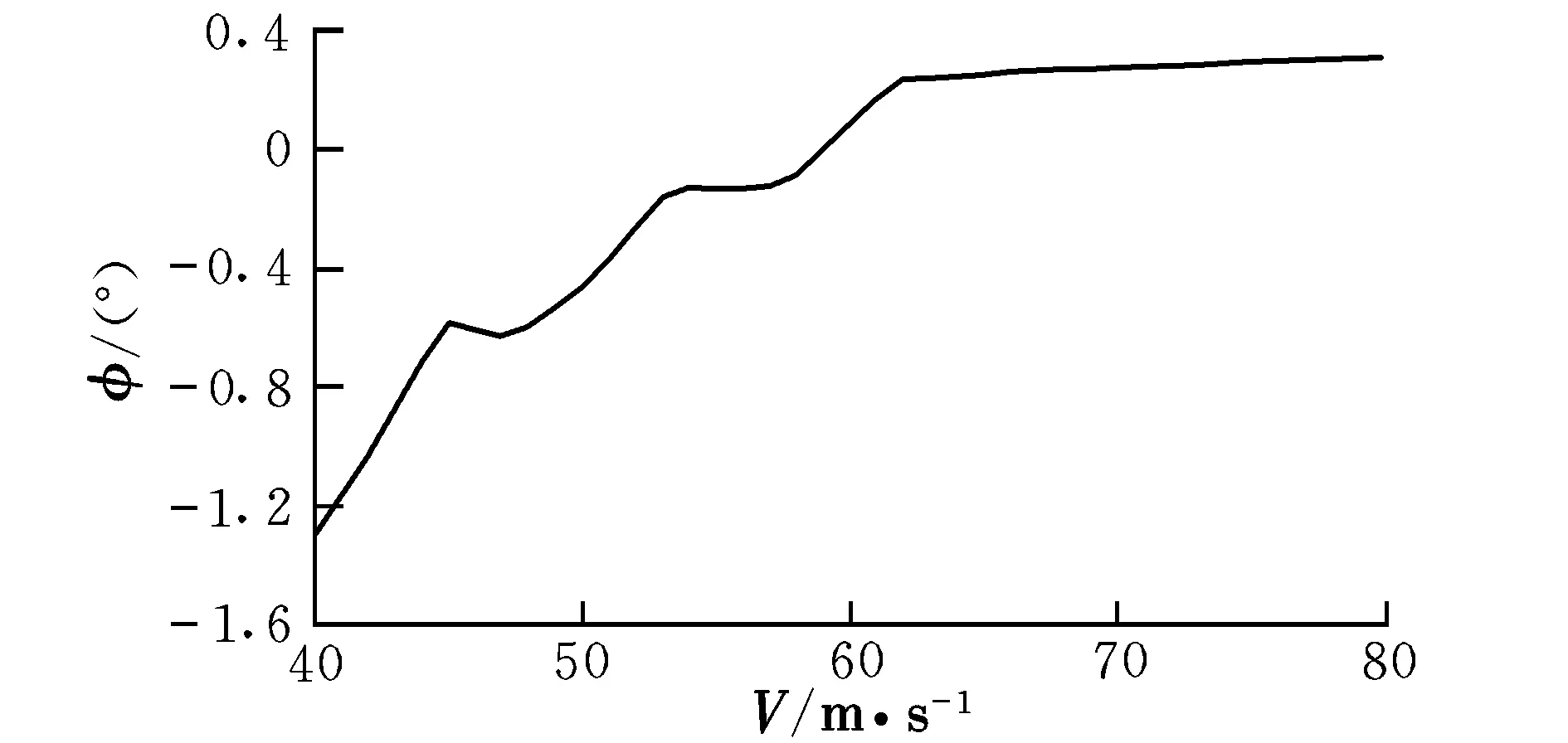
图5 配平滚转角随速度的变化曲线Fig.5 Trimming roll angle with different velocities

图6 配平升降舵偏转角随速度的变化曲线Fig.6 Trimming elevator angle with different velocities

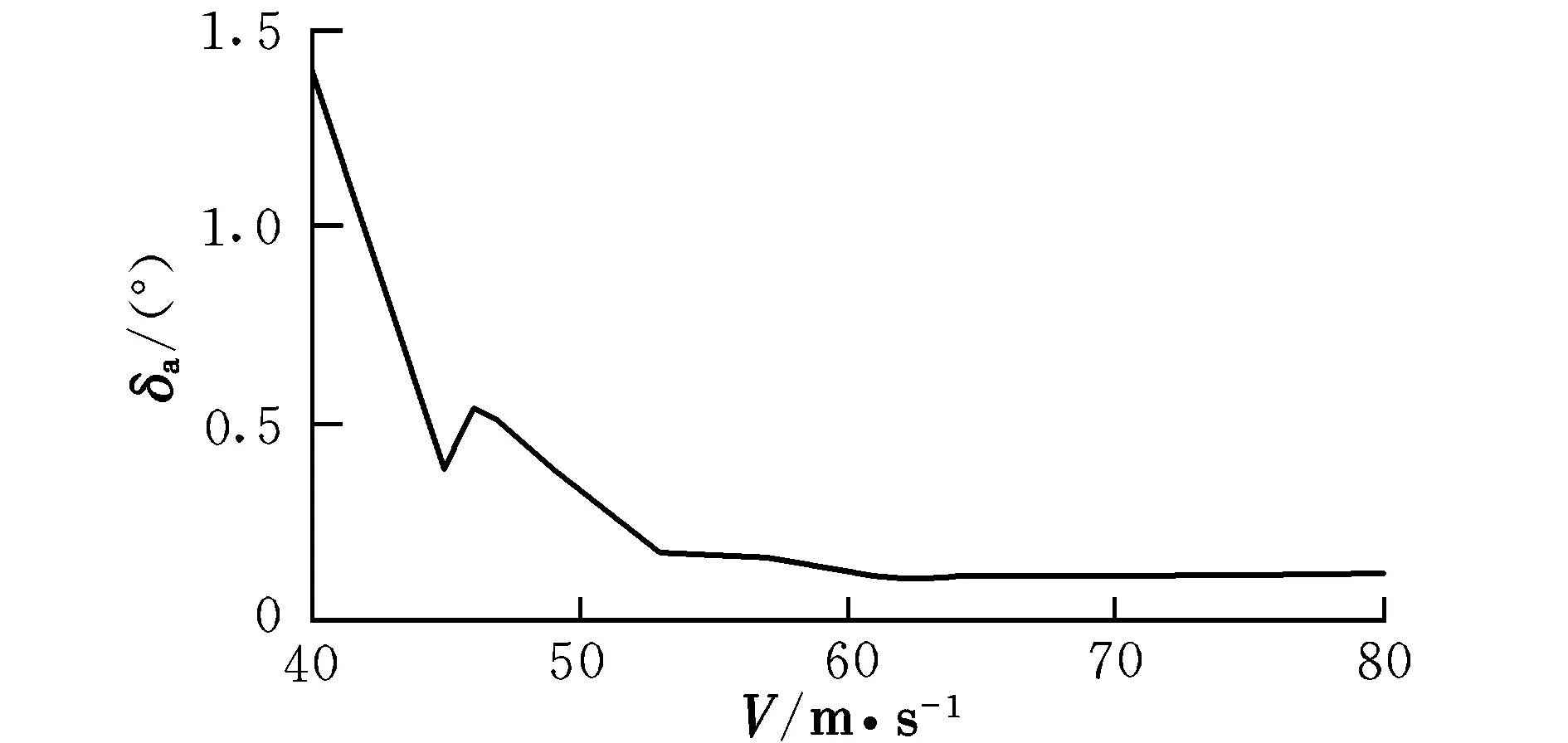
图7 配平副翼偏转角随速度的变化曲线Fig.7 Trimming aileron angle with different velocities

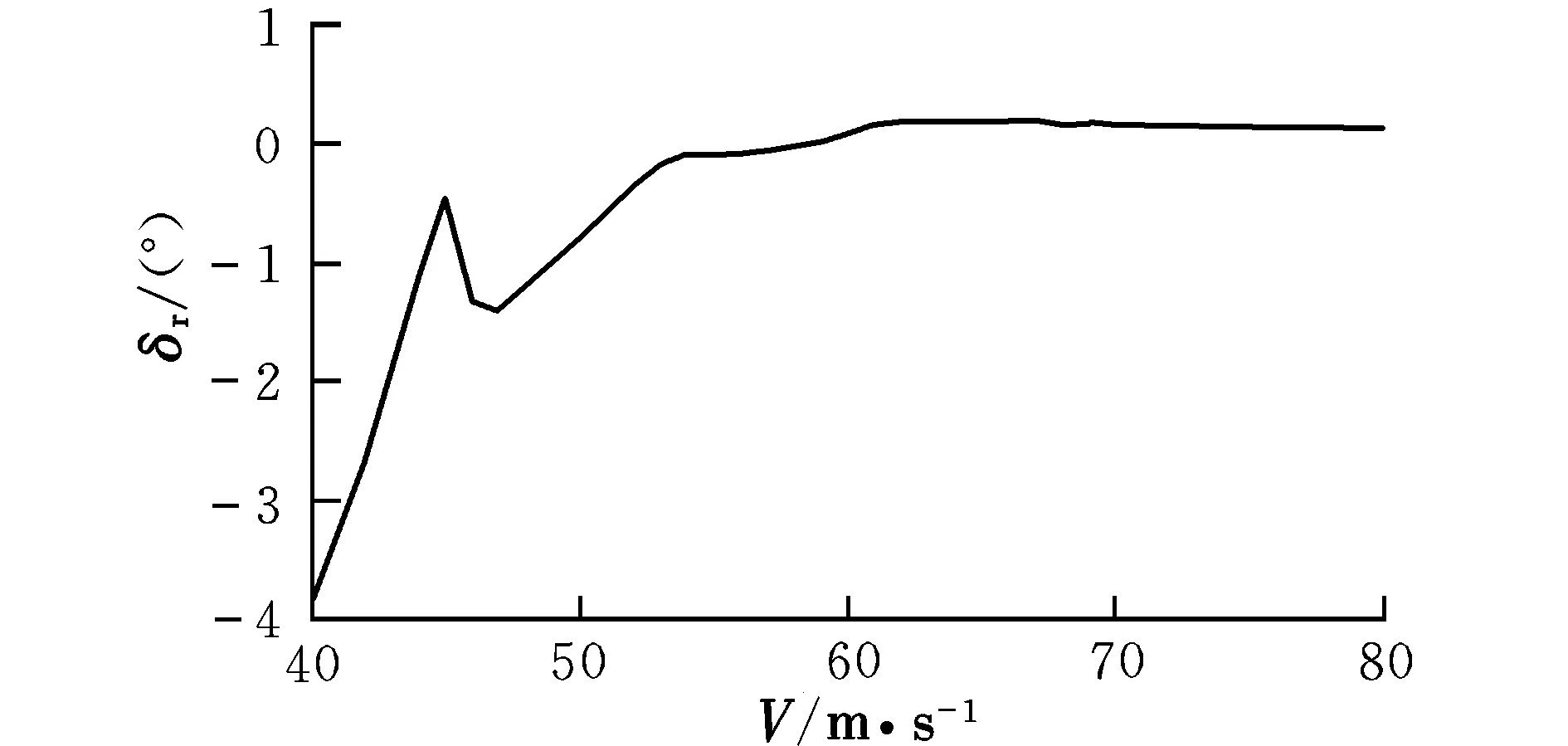
图8 配平方向舵偏转角随速度的变化曲线Fig.8 Trimming rudder angle with different velocities

由曲线图可知,在低速状态下,随着速度的提高,升降舵偏角反而减小,这时需要飞行员向前推杆以稳定飞行;在46 m/s之后,为保持在当前定常下滑飞行过程,需飞行员向后拉杆,符合飞行员的操纵习惯,而之前则为反操作区,该区域内的飞行平衡状态不可取。为了保持定常下滑状态,随着速度的提高,俯仰角不断变小,这是符合实际情况的。速度较小时,侧滑角及方向舵偏角需求越大,随着速度的提高,在51 m/s后,侧滑角保持在0°附近范围内的稳定状态,而在53 m/s后,方向舵偏角也逐渐进入稳定状态。实际飞行中,为了保持飞机对控制量的及时反应并出于安全性的考虑,是不允许飞机存在侧滑现象的,因此下滑速度选取应在53 m/s之后。随着速度的提高,迎角不断减小,在67 m/s后会出现负迎角情况,考虑到正常飞行迎角为正,故飞行速度不宜高于67 m/s。因该算例飞机的失速迎角为8.1°,对比图2可见,该迎角对应的失速速度约为50 m/s,而文献[12]中规定,进场下滑速度约为失速速度的1.1倍,因此,下滑初始速度为55 m/s。此飞行速度下对应的飞行参数分别为:

[T,α,β,θ,φ,ψ,δe,δa,δr]=

[1.684×104,5.059°,-0.007°,0.558°,-0.136°,

0,-0.663°,0.164°,-0.111°]

该速度下各个参数在该机气动条件限制范围之内,是合理的。

4 结论

本文在分析飞机定常下滑时平衡状态基本特征的基础上,提出了自适应变异算子人工鱼群算法的下滑配平新方法,得出的结论如下:

(1)针对人工鱼群算法的不足,本文考虑了包括鱼群个体之间的感知作用、群体的领导模式并结合萤火虫算法在内的群体行为特点对鱼群行为进行完善。采用自适应步长和视野并引入了Gauss变异算子和遗传算法，在一定情况下对鱼群个体进行变异操作。通过验证函数的测试表明，该算法在收敛速度、精度以及克服早熟能力方面都有了显著的提高。

(2)引入代价函数,将飞机下滑过程的配平问题转化为对代价函数最大值的求解问题,并很好地解决了常规数值方法对初值依赖性高以及单一智能算法易陷入局部最优等不足。仿真结果表明,该算法是一种有效的求解飞机平衡状态的方法。

参考文献：

[1] Pashilkar A A.Algorithms for aircraft trim analysis on ground[R].AIAA-96-3505-CP,1996.

[2] 杨超,洪冠新.求解非线性代数方程组的一种建议方法[J].飞行力学,1997,15(2):42-46.

[3] 沈宏良,刘昶.飞机平衡状态的优化计算方法[J].飞行力学,2001,19(4):15-18.

[4] 王海涛,高金源.基于混合遗传算法求解飞机的平衡状态[J].航空学报,2005,26(4):470-475.

[5] 张红梅,张国山.求解高超声速飞行器平衡状态的GA-SQP算法[J].航空学报,2012,33(1):138-146.

[6] 胡云安,左斌,李静.基于退火递归神经网络的极值搜索优化算法求解一类碟式飞行器的平衡状态[J].兵工学报,2008,29(3):341-347.

[7] 李晓磊,邵之江,钱积新.一种基于动物自治体的寻优模式:鱼群算法[J].系统工程理论与实践,2002,22(11):32-38.

[8] Huth A,Wissel C.The simulation of movement of fish schools[J].Journal of Theoretical Biology,1992,156(3):365-385.

[9] Couzin I,Krause J James.Collective memory and spatial sorting in animal groups[J].Journal of Theoretical Biology,2002,218(1):1-11.

[10] Christianne Dalforno, Diego Mostaccio. Increasing the scalability and the speedup of a fish school simulator[R].ICCSA 2008,Part II,LNCS 5073,2008.

[11] Juan Carlos González,Christianne Dalforno.A fuzzy logic fish school model[R].ICCS 2009,Part I,LNCS 5544,2009.

[12] 中国航空工业发展研究中心.国外舰载机技术发展[M].北京:航空工业出版社,2008:10,70.