基于微分对策的追逃对抗仿真
车竞, 郑凤麒
(中国空气动力研究与发展中心 计算空气动力研究所, 四川 绵阳 621000)
0 引言
微分对策理论是研究利益相互制约的双方策略选择的理性行为及相应结局的学科。1971年,美国科学家Friedman采用了两个近似离散对策序列精确定义了微分对策,建立了微分对策与鞍点存在性理论,从而奠定了微分对策理论的数学基础。
由于理论上的最优性,微分对策已广泛应用于战术导弹的制导律设计。Tahk等人[1]利用梯度法求解了微分对策制导的数值解,但模型非常复杂。Basar等[2]设计了离线的神经网络微分制导律。汤善同[3]利用微分对策强迫奇异摄动方法设计了零阶组合反馈制导律。罗生等[4]采用伴随理论求解了终端控制的微分对策最优制导问题。空战决策方面,“一对一”空战通常可比拟为二人零和定量微分对策问题。梅丹等[5]利用微分对策方法建立了以捕获时间tf为性能指标的二维单机追逃空战的决策模型。王发坤等[6]建立了三维空间追逃问题的定性微分对策模型。由于微分对策模型是典型的两点边值问题,数值求解通常采用梯度迭代法。黄力伟[7]提出了将梯度法和静态优化算法相结合的一类数值解法。泮斌峰等[8]通过终端时刻调节算法求解了终端时刻tf自由的两点边值问题。
本文应用微分对策理论,对纵向平面内导弹-飞机的追逃问题进行了研究,建立了数学模型,对于终端时刻tf自由的情况,通过内外环两次迭代得到了数值解,针对有控制能量最小要求和无控制能量最小要求两类性能指标下的微分对策模型,在双方不同的最大机动能力条件下进行了数值仿真,其模型和仿真结果可用于空战双方武器性能、制导控制设计评估,以及最优空战决策研究。
1 微分对策问题描述
对于攻防对抗的A和B双方,组成n维系统[8]:

(1)
式中,u(t),v(t)分别为A,B双方的控制向量。微分对策即要求解u(t)和v(t),使得在系统满足终端目标集ψ(tf,X(tf))=0的情况下,对于A方,达到性能指标J最小;对于B方,达到性能指标J最大。性能指标通常采用如下形式:

(2)

(3)
相应地,J*称为最优对策值,X*(t)称为最优迹线。
2 微分对策问题求解
2.1 求解基本方程
上述微分对策问题通常采用极小值原理进行求解,首先构造哈密顿函数:
H(X,λ,u,v,t)=L+λTf
(4)
式中,λ为哈密顿乘子,求解下述正则方程组可得到问题的最优解:
(5)

(6)
若终端时刻tf不固定,则还必须通过下述条件自然确定tf:
dJ/dt|tf=H(X*,λ*,u*,v*,t)|tf+∂φ/∂t|tf=0
(7)
2.2 数值计算方法

(1)置迭代步数i=0,j=0;
(3)任意选择uj(t),vj(t)作为初始策略;


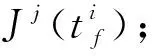
(8)更新控制量uj+1(t)=uj(t)-αgu(t),vj+1(t)=vj(t)+βgv(t)(α,β为无限小正数,由一维搜索算法确定),置j=j+1,返回步骤(4);

(10)检查收敛:当dtf≤ε2时,终端时刻迭代收敛,算法结束,否则置i=i+1,返回步骤(3)。
3 导弹-飞机的数学模型
考虑一个纵向平面内的导弹-飞机追逃问题,双方速度大小不变,速度方向的改变量为控制量,追逐方(导弹,用下标D表示)运动方程为:
(8)
式中,xD,yD,vD,θD分别为导弹的纵横坐标、速度和倾角。逃避方(目标,用下标M表示)运动方程为:
(9)
式中,xM,yM,vM,θM分别为目标的纵横坐标、速度和倾角。令:
(10)
得到双方纵向平面内追逃系统的状态方程为:
(11)
设性能指标(支付函数)为:
(12)
4 仿真结果及分析
4.1 仿真示例1



图1 追逃问题的微分对策仿真结果1Fig.1 The first differential game simulation results of the pursuit-evasion resistance
4.2 仿真示例2
在上述性能指标中减去控制能量约束,即:

(13)
采用相同的设置,追逐方(导弹)的最大机动能力是逃避方(目标)的4倍、1倍、2/3和1/3,双方轨迹如图2所示。对策时间分别为73.42 s,54.92 s,40.62 s,31.43 s。



图2 追逃问题的微分对策仿真结果2Fig.2 The second differential game results of pursuit-evasion resistance
5 结束语
本文建立了纵向平面内空战双方追逃对抗的微分对策数学模型,采用极小值原理和梯度迭代法对飞机-导弹纵向平面内的追逃问题进行了数值仿真,得到了双方不同机动能力下的追逃仿真结果。从仿真结果可以看出,追逃双方均以最大机动能力机动,当双方最大机动能力之比不同时,得到捕获、接近或摆脱几种对策结果。微分对策中,当tf自由时,其迭代计算耗时远大于tf固定的情况,难以在空战中应用以实时在线生成航迹,因此在实时空战仿真中,可将整个对抗过程分为若干段,在每一时间段内进行微分对策,即可满足实时在线航迹生成的要求。本文的研究成果可用于防空导弹作战效能评估、一对一空战对抗双方的最优决策研究。
参考文献:
[1] Tahk Min-Jea,Ryu Hyeok,Kim Je-Gyum.An iterative numerical method for a class of quantitative pursuit-evasion games[R].AIAA-98-4118,1998.
[2] Basar T,Olsder G J.Dynamic noncooperative game theory[M].New York:Academic Press,1995.
[3] 汤善同.微分对策制导规律与改进的比例导引制导规律性能比较[J].宇航学报,2002,23(6):38-42.
[4] 罗生,宋龙.微分对策制导[J].航空科学技术,2011,(3):68-70.
[5] 梅丹,吴文海,徐家义.现代战机空战对策模型研究[J].飞机设计,2007,27(2):69-73.
[6] 王发坤,秦艳琳.三维空间中追逃对抗定性微分对策模型研究[J].船舶电子工程,2008,28(7):8-10,175.
[7] 黄力伟.求解微分对策问题的混合法[J].火力与指挥控制, 2011,36(1):50-52.
[8] 泮斌峰,唐硕.吸气式空天飞行器闭环上升制导研究[J].飞行力学,2010,28(6):48-51.

