带节能砌体填充墙的RC框架抗震试验研究

黄 靓, 易宏伟,王 辉，蒋文龙

(湖南大学 土木工程学院，湖南 长沙 410082)

填充墙作为框架结构中的非结构构件，设计中并未充分考虑其对框架结构的影响，然而，其对框架结构抗震性能的影响却不容忽略[1-4]．国内外研究者在这方面做了重要的工作[3,5-7]，其中土耳其的Marjani等人使用低周反复荷载对6个两层单跨带填充墙的框架进行了试验和有限元模拟研究．研究表明：填充墙能够极大地提高框架的强度和刚度．黄群贤等人对4榀单层单跨填充墙RC平面框架试件进行抗震性能试验，试验表明：不同砌块填充墙对框架结构具有明显的刚度效应.研究者主要针对平面框架进行研究，对带填充墙的三维立体框架(以下简称立体框架)研究较少，而立体框架充分反应了平面框架之间的受力协调能力，其受力机制能够更好地代表整体结构的特性，因此对立体框架的进一步研究很有必要.墙体节能在建筑节能中占有重要的地位，因此节能砌块被选为本文的墙体材料.本文对带节能砌体填充墙(以下简称填充墙)的框架结构与空框架进行对比试验研究，从而得到节能砌体填充墙对框架结构的滞回特性、承载力、抗侧刚度以及强度的影响规律，并从受力机制方面揭示了节能砌块填充墙与框架的共同工作原理.

1 试验概况

1.1 试件设计与制作

试件设计参考《抗震设计规范》(GB50011-2010)[8]的要求，共设计了2个单跨立体框架，其中一个为不带填充墙的空框架，另一个为带填充墙的RC框架，编号分别为CF-1和CF-2.试件CF-2研究带填充墙框架结构的抗震性能，试件CF-1用作对比.

试件根据相似理论按照1∶4比例缩尺设计而成.两试件的框架部分几何尺寸及配筋完全相同，柱截面尺寸为150 mm×150 mm，梁为70 mm×100 mm，基础采用0.4 m厚的底板，板平面尺寸为2.0 m×2.0 m，砌体与框架柱之间每隔600 mm配置了2A6的拉筋，框架几何尺寸及截面配筋如图1所示.

梁柱纵筋、箍筋均采用HRB335，考虑试件为缩尺模型，钢筋强度按略低于《混凝土结构设计规范》(GB50010-2010)[9]的要求进行设计，混凝土强度为C30，材料实测力学性能见表1，砌块采用多排孔节能砌块，砌块标准块型几何尺寸为190 mm×190 mm×115 mm，强度等级采用MU5，单块砌块的抗压强度为6.5 MPa，砂浆立方体抗压强度为4.6 MPa，考虑模型缩尺的影响，砌块厚度切割成标准块厚度的1/4，模拟1/4砌体墙厚，多排孔节能砌块砌体如图2所示.

图1 试件几何尺寸及配筋(单位：mm)Fig.1 Specimen geometry and steel detailing (mm)

表1 材料基本参数Tab.1 Parameters of specimens

图2 节能混凝土砌块砌体Fig.2 Energy conservation concrete block masonry

1.2 试验方案

1.2.1 测点布置与数据采集

试件的位移测点设在底板、1层和2层层顶，底板和1层各布置了两个量程为50 mm的位移计，2层布置了两个量程为100 mm的位移计，每层的侧向位移取两个位移的平均值，在各层的关键部位设置了钢筋电阻应变片，柱的应变片布置在各层的柱底与柱顶，梁的应变片布置在梁的两端.

试验过程中的量测仪器主要为DH3818静态应变采集仪，可读取应变片的应变值及位移传感器的量测数值，加载作动器的水平位移、水平荷载由电伺服加载系统(MTS)测得，并利用采集的荷载和顶点位移数值绘制试件的滞回曲线.试验中，人工观察裂缝出现时对应的力和位移，及时标注在试件上的相应位置.

1.2.2 加载装置

加载装置见图3，图3两试件均采用同样的加载装置.试件底板水平方向用千斤顶和钢梁固定，竖直方向由钢压梁和地脚螺栓固定.竖向荷载由液压千斤顶加载，通过工字钢和混凝土顶梁把荷载平均分配到各框架柱的顶部；水平荷载由量程为1 000 kN的电液伺服作动器加载，通过钢梁传递到试件上，在试件与钢梁之间用矩形钢垫块确保加载中心点位于第二层柱顶，拉力由圆钢拉杆传递.

图3 加载装置Fig.3 Test setup

1.2.3 加载方案

本试验模拟15层混凝土框架结构的底部两层地震反应．加载方案参照《建筑抗震试验方法规程》(JGJl01-96)[10]，首先施加竖向力，用以模拟上部13层的重力及楼屋面荷载．计算得到的柱轴压比约为0.25，控制液压油泵，使得轴压比为0.25，等竖向压力稳定后再进行水平预加载．试验的水平加载程序分为预加载和正式加载两个阶段，正式加载采用分级循环对称加(卸)载．在试件开裂前采用荷载控制加载，每级荷载循环一次，试件出现裂缝后，每级位移增量为一倍开裂位移，每级位移循环两次，直至试件破坏或者降至最大荷载的85%，终止试验.

2 试验过程

本试验主要研究的是带节能砌体填充墙框架结构的抗震性能，根据试验现象，试件破坏过程按照裂缝开展的特点可分为三个阶段：开裂阶段、裂缝开展阶段和破坏阶段.

试件CF-1：当水平推力加到57 kN时，一层框架柱的柱底部出现一条微小的横向裂缝，此时的位移值为6 mm．之后改变加载制度，用位移进行控制，每一级位移的增量为6 mm．随着位移的进一步增大，在底层梁的端部开始出现了细小的裂缝．当位移加到18 mm时，二层柱顶出现裂缝，柱脚的裂缝进一步发展贯通．位移加到20 mm之后，荷载增长速度明显减慢，裂缝进一步发展，梁两端出现了大量的裂缝．当位移加到55 mm时，水平荷载明显下降．此时，框架柱脚的混凝土有局部脱落的现象，继续加载，当最终荷载降为最大荷载的85%时，即认定框架已经达到了极限状态，此时柱脚已经完全被压碎剥落，出现明显的破坏迹象，试件CF-1停止加载.最终破坏如图4所示.

试件CF-2：当水平推力加到118 kN时，一层框架梁端部及填充墙出现一条微小的斜裂缝，此时的位移值为6 mm．之后改变加载制度，用位移进行控制，每一级位移的增量为6 mm．随着位移的进一步增大，当位移加到10 mm时，二层柱顶以及梁中部出现裂缝，填充墙的裂缝进一步发展．位移加到20 mm之后，水平荷载明显下降，此时，填充墙出现大量的阶梯型裂缝，同时一层柱中下部及二层柱顶也出现大量的裂缝．继续加载，当最终荷载降为最大荷载的85%时，即认定框架已经达到了极限状态，此时填充墙出现较宽的阶梯型裂缝，并有部分砌块出现压碎现象，试件CF-2停止加载.最终破坏如图5所示.

图4 图4 试件CF-1破坏图Fig.4 Failure of specimen CF-1

图5 试件CF-2破坏图Fig.5 Failure of specimen CF-2

3 试验结果分析

3.1 滞回特性

试件在低周反复荷载下的滞回曲线综合反映了试件的抗震性能[11-12]，包括结构的承载力、耗能能力、变形特征和刚度特性等.两个模型的顶点水平荷载-位移曲线如图6所示，从图6可以看出：

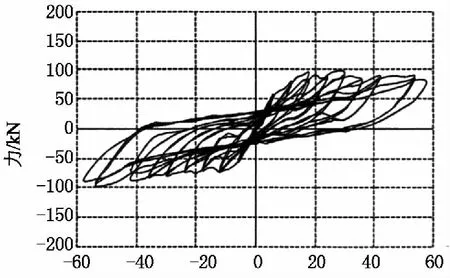
位移/mm(a)试件CF-1

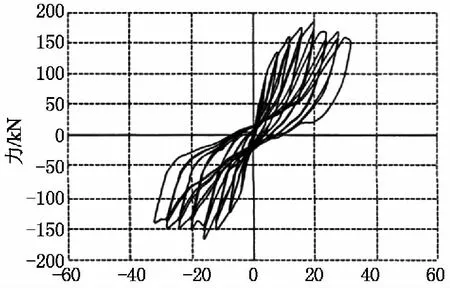
位移/mm(b)试件CF-2图6 试件滞回曲线Fig.6 Hysteresis curves of the specimens

两试件开裂之前，滞回曲线基本呈一条直线，围成的面积很小，刚度变化很小，几乎没有残余变形，结构还处于弹性阶段．随着荷载的增加，滞回环略显饱满的弓形，表现出较好的耗能性能．

两试件在梁端出现塑性铰之后，滞回环出现了捏拢现象，荷载继续反复作用，混凝土受拉裂缝不断地开展和延伸，钢筋拉应变和混凝土压应变不断地积累增大，总变形持续地增加，而承载力变化不大．

试件CF-2较试件CF-1，承载力明显增加，而变形相应减小，这说明填充墙能够提高框架的承载能力和侧向刚度，而相应的减少框架的侧向变形．

在同一位移条件下，CF-2比CF-1的滞回曲线饱满，说明填充墙提高了框架的耗能能力.

3.2 骨架曲线

利用试件的荷载-位移骨架曲线图，可以确定构件的屈服荷载、最大承载力、强度退化和延性等主要特征．试件的屈服荷载Py和屈服位移Δy由等效面积法[13]进行确定，峰值荷载Pm和峰值位移Δm即取骨架曲线的最高点，而极限荷载Pu和相应的侧移Δu则取试件在最大荷载出现后随侧移的增加而荷载降至最大荷载的85%时的相应荷载和相应侧移.延性系数作为衡量结构抗震性能的一个重要指标，是指破坏时的极限位移Δu和屈服位移Δy的比值，其中延性系数取正向和负向的平均值.试验试件骨架曲线图及主要试验结果见图7与表2，从中可以看出：

CF-2试件和CF-1试件相比，结构整体的屈服荷载、峰值荷载和极限荷载都有较大的提高，前者的最大承载力为后者2倍左右.此结果说明带填充墙的混凝土框架结构在循环荷载下，填充墙分担了几乎一半的水平荷载．

试件CF-2与CF-1相比，结构的屈服位移、峰值位移和极限位移都下降了40%左右．这说明填充墙对框架的约束效应明显降低了框架的变形能力，从而使得框架结构的各项位移指标减小．

CF-2的延性系数为CF-1试件的60%，说明填充墙和框架的相互作用，将很大程度上降低框架的延性.

位移/mm图7 试件骨架曲线Fig.7 Skeleton curves of specimens

表2 骨架曲线特征点结果Tab.2 Characteristic values of skeleton curves

3.3 刚度退化

在位移幅值不变的条件下，结构构件的刚度随反复加载的次数增加而降低的特性即为刚度退化．结构刚度的退化即为结构性能的退化.在试验过程中，裂缝的增多、位移的增大以及循环次数的增加都会导致结构刚度的退化，试验的刚度参照 《建筑抗震试验方法规程》[10]的割线刚度法进行计算，刚度退化试验结果见图8和表3.

位移/mm图8 刚度退化曲线Fig.8 Stiffness degradation curves

表3 刚度退化曲线特征点结果Tab.3 Characteristic values of stiffness degradation curves (kN/mm)

从表3可知框架CF-1的初始刚度为10.9 kN/mm，开裂刚度为初始刚度的85.6%，屈服刚度退化为32.2%，峰值刚度退化为15.4%，极限刚度最后退化为13.2%．框架CF-2的初始刚度为24.7 kN/mm，开裂刚度为初始刚度的89.9%，屈服刚度退化为51.8%，峰值刚度退化为33.3%，极限刚度最后退化为18.3%，其中框架CF-2的初始刚度为框架CF-1的2.3倍.

从以上分析中可以看出，填充墙可以大幅度增加框架结构的初始刚度.虽然带填充墙的试件CF-2的刚度退化比CF-1快，但是其破坏刚度依然较大，还是能保证框架结构的后期承载能力并具备较强的抗倒塌能力.

3.4 强度退化

试件加载到同一加载位移时，试件的承载力会随着循环加载次数的增加而逐渐降低.根据JGJ101-96《建筑抗震试验方法规程》[10]的建议，本文采用试件的强度退化系数来描述结构强度退化的变化规律．强度退化系数是指试件加载过程中，同级加载各次循环的峰值荷载与该级加载第一次循环所得的峰值荷载的比值.本文利用试验加载所得到的荷载-位移曲线，根据公式(1)，计算确定了试件的强度退化系数，具体计算结果如图9所示.

式中：λi——i幅值时试件的强度退化系数；Pi2——i幅值时第二次循环的峰值点荷载；Pi1——i幅值时第一次循环的峰值点荷载.

从图9可以看出，两试件在同级荷载作用下，其强度退化系数始终保持在0.9以上，说明两试件的承载力退化程度小，可以推断，试件在破坏后仍保有较高的继续承载能力.比较两试件可以看出，带填充墙的框架CF-2强度退化现象较CF-1严重.因为砌体的脆性特质以及填充墙的大量开裂，逐步退出工作，从而导致框架CF-2的强度退化明显.

位移/mm(a)试件CF-1

位移/mm(b)试件CF-2图9 强度退化曲线Fig.9 Strength degradation curves

4 受力机制分析

从受力方面分析，CF-1在承受水平推力时，由于水平力全部是由柱脚传给基础，框架柱的柱脚将产生较大的剪力和弯矩，而框架梁主要是受压以及梁柱节点的变形而产生较小的弯矩，因此，框架柱要先于框架梁屈服，同时也先破坏．CF-2在水平力的作用下，由于填充墙的支撑作用分担了部分水平力，从而提高了框架的承载能力，同时由于填充墙对框架的约束效应使得框架的变形能力变差.CF-2与CF-1比较，从柱上的裂缝分布情况看，柱中下部裂缝明显增多，且柱脚并没有出现明显的破坏迹象．这主要是因为填充墙改变了框架柱的内力分布，使得框架的破坏从剪切型向弯曲型过渡，同时柱脚得到了保护，使得柱脚并未出现明显的破坏迹象.砌体抗剪强度大于砂浆抗剪强度且砌体本身具有明显的脆性，因此试验中填充墙上出现了沿砂浆灰缝较宽的阶梯型裂缝，并有部分砌块出现压碎的现象.

5 结 论

通过对两个框架结构的抗震试验研究，得出下列结论：

在RC框架结构中，节能砌体填充墙能够提高框架的承载能力，但是相应降低了框架结构的延性，其中试验中带砌体填充墙的框架承载力为空框架的1.87倍，延性系数只有空框架的60%.

在同一位移条件下，带节能砌体填充墙的框架滞回曲线饱满，说明填充墙提高了框架的整体耗能能力，同时填充墙比框架先退出工作，为框架多提供了一道抗震防线，从而提高了框架的抗震能力.

节能砌体填充墙对框架的约束效应使得框架结构的侧移减小，从而保证框架的侧移能够更好地满足规范要求，其中试验中结构的屈服位移、峰值位移和极限位移都下降了40%左右.

节能砌体填充墙可以大幅度增加框架结构的初始刚度，试验中其初始刚度为空框架的2.3倍.虽然带填充墙的框架刚度退化较快，但是其极限刚度依然较大，仍具备较强的抗倒塌能力.

由于砌体的脆性特质以及填充墙的大量开裂，使得带节能砌体填充墙的框架强度退化较空框架严重，然而其强度退化系数始终保持在0.9以上，说明其强度退化程度较小，因此可以推断，试件在破坏后仍保持了较高的继续承载能力.

[1] 郭子雄,吴毅彬,黄群贤.砌体填充墙框架结构抗震性能研究现状与展望[J].地震工程与工程震动,2008,28(6): 172-177.

GUO Z X, WU Y B, HUANG Q X. Research and development in seismic behavior of infilled-frame structures[J].Journal of Earthquake Engineering and Engineemng Vibration,2008,28(6):172-177.(In Chinese)

[2] FLANAGAN R, BENNETT R. In-plane analysis of masonry infill materials[J]. Pract Period Struct Des Constr,2001,6(4):176-182.

[3] 黄群贤,郭子雄,朱雁茹,等.混凝土空心砌块填充墙RC框架抗震性能试验究[J].建筑结构学报,2012,33(2):110-118.

HUANG Q X, GUO Z X,ZHU Y R,etal. Experimental study on seismic behavior of RC frames infilled with concrete hollow blocks[J]. Journal of Building Structures, 2012,33(2):110-118. (In Chinese)

[4] 邹昀.带砌体填充墙的钢筋混凝土框架受力性能分析[J].江南大学学报,2002,1(1):76-81.

ZOU Y. Study of reinforced concrete frame infilled with brick panels[J]. Journal of Southern Yangtze University，2002,1(1)：76-81. (In Chinese)

[5] MADAN A, HASHMI A K. Analytical prediction of the seismic performance of masonry infilled reinforced concrete frames subjected to near-field earthquakes[J]. Journal of Structural Engineering,2008,134(9):1569-1581.

[6] CHIOU Y J,TZENG J C, LIOU Y W. Experimental and analytical study of masonry infilled frames[J]. Journal of Structural Engineering,1999,125(10):1109-1117.

[7] MARJANI F, ERSOY U. Behavior of brick infilled reinforced concrete frames under reversed cyclic loading [J]. ISSEE, 2002, 62(2):142-150.

[8] GB50011-2010 建筑抗震设计规范[S].北京：中国建筑工业出版社,2010.

GB50011-2010 Code for seismic design of buildings[S].Beijing: China Architecture and Building Press,2010.(In Chinese)

[9] GB50010-2010 混凝土结构设计规范[S].北京：中国建筑工业出版社,2010.

GB50010-2010 Code for design of concrete structures[S].Beijing: China Architecture and Building Press,2010.(In Chinese)

[10] JGJ101-96 建筑抗震试验方法规程[S].北京：中国建筑工业出版社,1997:10-30.

JGJ101-96 Specificating of testing methods for earthquake resistant building[S]. Beijing: China Architecture and Building Press,1997:10-30.(In Chinese)

[11] 范苏榕.钢支撑加固钢筋混凝土框架结构的试验研究[D].南京：南京工业大学,2002:8.

FAN S R. Experimental researeh on the aseismic retrontting of reinforced conerete frame structures with steel braces[D].Nanjing: Nanjing University of Technology,2002:8. (In Chinese)

[12] 朱伯龙. 结构抗震试验[M].北京：地震出版社,1989.

ZHU B L. Structural seismic test [M]. Beijing: Earthquake Press,1989.(In Chinese)

[13] XIAO J Z, SUN Y D, FALKNER H. Seismic performance of frame structures with recycled aggregate concrete[J]. Engineering Structures, 2006,28(1):1-8.