考虑桩-土相互作用的悬臂式排桩内力计算方法研究

赵明华，李 文，张 锐

(湖南大学 岩土工程研究所，湖南 长沙 410082)

当基坑开挖深度不大且土性条件较好时，可采用悬臂式排桩进行支护[1].目前悬臂式排桩内力计算常用的方法有：静力平衡法、弹性法和共同变形理论三种[1-3].静力平衡法是将支护桩的入土深度和土压力零点视为未知量，根据力的平衡条件或力矩平衡条件加以求解的方法.该法概念明确、计算简便，在工程中广为采用.但静力平衡法将支护桩侧土压力简单地按主、被动土压力计算，不考虑桩-土之间的相互作用和变形协调条件，存在较大的计算误差[3].弹性法将水土压力作为已知荷载，将单位宽度的桩墙或单桩(按有效截面宽度计算)视为设置于弹性地基上的梁，再根据通用弹性地基梁法求解结构内力和变形.该法考虑了桩身各微段的平衡条件，可在一定程度上分析桩-土相互作用机理，计算参数少且积累了较多工程经验，是实际工程中一种重要的设计方法和手段[2-3].但弹性法一般只考虑土体抗力与桩身位移间的线性函数关系[4-5]，与实际不符.共同变形理论将基坑内、外侧土体简化为土弹簧，假定在初始时刻各弹簧压力均处于静止土压力的基准状态，随着桩侧位移的增大不断向主动或被动土压力状态变化，通过调整桩身位移直到满足平衡条件，从而计算桩侧土压力和桩身内力[1].该法能较好地考虑桩-土相互作用机理，但其计算过程繁琐，所用地基反力系数与通用弹性地基法的相关参数具有不同的意义，取值缺乏工程经验积累.

由上面的讨论可以看出，常用的悬臂式排桩内力计算方法均存在一些不合理之处.为此，本文通过引入非线性的桩-土相互作用模型，提出一种可充分考虑桩-土共同作用机理的悬臂式排桩内力计算方法.

1 考虑桩-土相互作用的悬臂式排桩内力计算方法

悬臂式排桩内力计算的关键是如何分析桩-土相互作用的规律[6-8].常用的计算方法中，弹性法便于编制通用的计算机程序，但是未充分揭示桩-土相互作用机理.为此，本文将弹性法和共同变形理论相结合，提出一种能较好地考虑桩-土相互作用规律且便于编制通用计算机程序的悬臂式排桩内力计算方法，详细的计算过程如下．

1.1 单元离散

将支护桩从桩顶开始沿竖向划分为一系列的杆单元，设单元总数为N，则节点总数为N+1个.为了计算方便，尽可能在支护桩截面变化点、土压力突变点、基坑坑底等处设置节点.

1.2 单元刚度矩阵

如图1所示，某长度为L的杆单元Ei，其节点Ni，Ni+1处作用的剪力和弯矩分别为Vi，Mi和Vi+1，Mi+1，单元两端的位移和转角分别为ui，θi和ui+1，θi+1，则由结构力学中自由式梁单元的转角位移方程和叠加原理，可得杆端力与杆端位移的关系为[3]：

(1)

图1 杆单元受力与变形示意图Fig.1 Bar element and its deformation

式(1)即为单元刚度方程，可写成如下的紧密形式：

[K]e{δ}>e={R}>e．

(2)

其中，{R}>e为单元荷载列阵；{δ}>e为单元位移列阵；[K]e为单元刚度矩阵，其形式如下：

(3)

1.3 合成总体刚度矩阵

合成总体刚度矩阵实际上就是根据单元编号将各单元刚度矩阵“首尾相加”拼装成一个大的矩阵，拼装过程如图2所示[3].若单元总数为n，则总体刚度矩阵[K]的阶数为(2n+2)×(2n+2).

图2 总体刚度矩阵的合成示意图Fig.2 Global stiffness matrix and its composition

1.4 节点荷载列阵

大量研究成果表明，支挡结构所受土压力随结构位移不同而非线性变化[6-10].其中基坑外侧土压力由静止土压力的初始状态逐渐向主动土压力的极限状态发展，而基坑内侧土压力从静止土压力的初始状态向被动土压力的极限状态发展.为此，本文假定桩身某节点所受基坑外侧和内侧土压力与该节点侧向位移间分别满足如下的函数关系：

(i=1, 2, …,n+1)；

(4)

(i=1, 2, …,n+1)．

(5)

不同土性条件下，土体达到主动或被动极限状态所需的挡土结构位移量是不同的，一般而言，其取值范围满足如下关系[7-10]：

δa=(0.001～0.004)H，

(6)

δp=(0.01～0.1)H．

(7)

其中，δa，δp分别为达到主动和被动土压力所需支挡结构位移量，H为挡土结构高度.将式(6)，(7)代入式(4)，(5)中，并令(1-e-cδi)=0.96(即假定完成从初始土压力到极限土压力转化值的96%时，认为土体已达到极限状态)，可以得到土压力变化控制参数c1，c2的取值范围如下：

c1=(800～3 200)/H1，

(8)

c2=(32～320)/H2．

(9)

其中H1为桩长；H2为嵌固深度.

建立了各节点荷载与节点位移间的函数关系，则节点荷载函数列阵可以表示为

{R}>={R1}>-{R2}>．

(10)

其中，

1.5 总体刚度方程及其求解

形成了总体刚度矩阵和节点荷载函数列阵后，结构刚度方程可以表示为：

[K]{δ}>={R}>．

(11)

式中：[K]为总体刚度矩阵；{δ}>为待求的节点位移列阵；{R}>为节点荷载列阵.式(11)表示的结构刚度方程实际上是一非线性方程组，为了计算得到节点位移列阵{δ}>，可以采用非线性方程组的Newton-Raphson法进行迭代求解[15]，其过程如下．

1)为了表示方便，将式(11)改写成如下形式

F({δ}>)=[K]{δ}>-{R}>=0．

(12)

其中，F({δ}>)表示不平衡荷载列阵，其余符号意义同前.

2)设第k次迭代的节点位移列阵{δ}>k已知，其中k=0时取{δ}>k=[0, 0, …, 0]T.将第k+1迭代对应的方程组F({δ}>k+1)=0按泰勒级数展开，并取线性项，得如下的线性方程组

式中：{δ}>k为第k次迭代的节点位移列阵；{δ}>k+1为第k+1次迭代的节点位移列阵；{dδ}>为节点位移列阵的增量，且满足{dδ}>={δ}>k+1-{δ}>k；F({δ}>k)为第k次迭代的不平衡荷载列阵；F({δ}>k+1)为第k+1次迭代的不平衡荷载列阵；F′({δ}>k)为与第k次迭代的节点位移列阵对应的切线矩阵，其形式如下：

式(14)中元素∂Fi/∂δj(i,j=1,…,n+1)表示函数Fi对节点位移δj的偏导数.

3)求解线性方程组(13)得到节点位移增量列阵{dδ}>，即

{dδ}>=-[F′({δ}>k)]-1F({δ}>k)．

(15)

则第k+1次迭代的结构位移列阵为

{δ}>k+1={δ}>k-[F′({δ}>k)]-1F({δ}>k)

(16)

4)判断计算是否收敛，判断准则如下．

力收敛：

‖F({δ}>k+1)‖<εR‖F({δ}>1)‖；

(17)

位移收敛：

‖{dδ}>k+1‖<εδ‖{dδ}>1‖．

(18)

其中，εR和εR为两个常数.

5)若收敛则计算终止，将当前的结构位移列阵{δ}>k+1作为最终解答；若不收敛，则令k:=k+1，进行下一次迭代直到收敛为止.

1.6 单元杆端力和节点土压力

求出了节点位移列阵{δ}>后，可根据单元刚度方程(2)计算各单元的杆端力，然后根据单元杆端力(包括剪力和弯矩)绘出支护桩身内力图.同样地，由于支护桩侧的土压力荷载为节点位移的函数，将节点位移列阵代入式(4)和式(5)中，可计算得到基坑内外两侧支护桩所受的土压力荷载分布.

2 本文方法与经典方法的对比

为验证本文方法的合理性，现采用本文方法和经典的弹性地基梁法对某基坑悬臂式排桩进行内力计算，并将计算结果进行对比分析.计算参数如下：基坑开挖深度H1=4 m，排桩嵌固深度H2=6 m，桩径为d=1.5 m，桩身混凝土弹性模量为E=25×106kPa，基坑周围土质均匀，土体重度为γ=18kN/m3，c=0，φ=30°.采用经典法计算时，弹性地基反力的比例系数m=10 000.

从图3(a)可以看出，本文方法计算的桩身水平位移明显大于经典弹性地基梁法计算的桩身水平位移.从图3(b)和(c)可以看出，本文方法计算的桩身最大剪力和弯矩值也大于按经典弹性地基梁法计算的结果.这是因为经典的弹性地基梁法仅考虑桩侧土体抗力与桩身位移间的线性函数关系，即土体抗力可以随桩侧位移增大而不断增大，因此有可能出现桩侧土压力大于被动土压力的情况，过高地估计了土体的抗力值.另外，经典方法将基坑外侧土压力直接按主动土压力计算，荷载取值明显偏小.实际上，基坑外侧土体是处于静止土压力与主动土压力之间的“中间状态”，因此实际的土压力值要远大于按主动土压力计算的结果.从上述分析可以看出，经典方法过高地估计了土体的抗力，而过低地估计了基坑外侧的土压力荷载，因此计算结果偏于危险.本文方法通过考虑桩侧土压力与桩身位移间的非线性函数关系，较好地克服了经典方法的上述缺点，因而计算结果更为合理.

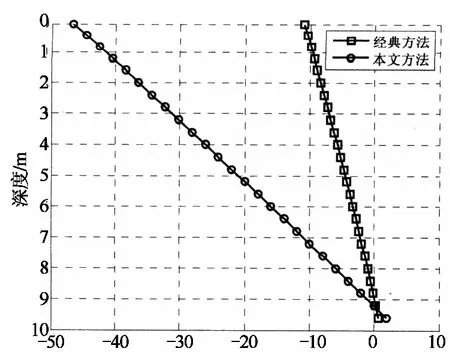
水平位移/mm(a) 水平位移分布图

剪力/kN(b) 剪力分布

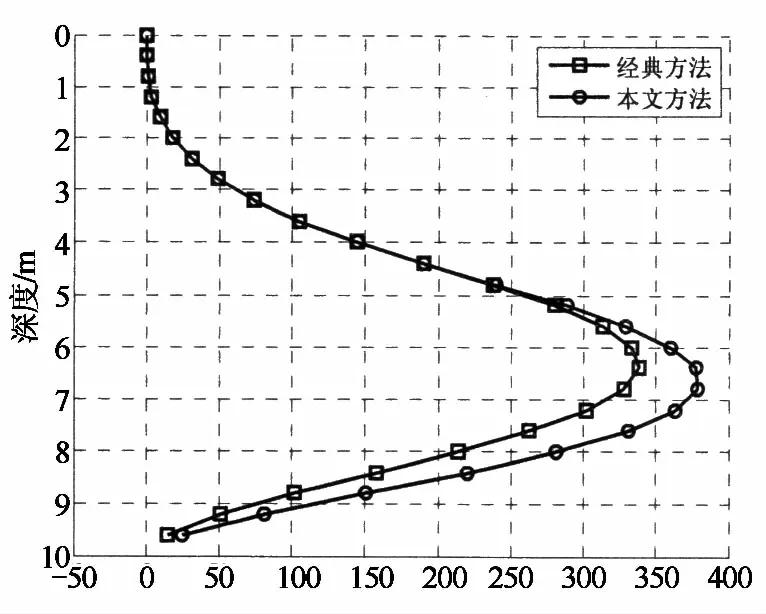
弯矩/(kN·m)(c) 弯矩分布图3 新方法与经典方法的比较Fig.3 Comparison between new method and traditional method

3 工程应用实例及影响因素分析

长沙市简牍博物馆绿化广场及停车场建设项目是长沙市的重点工程.工程场地位于长沙市城南路与建湘路交汇处的东北侧，周边建筑物及地下管线密布，工程地质条件较为复杂.为避免对既有建筑物和地下管线造成不良影响，基坑的开挖不能采用放坡处理，需进行必要的支护.其中北侧受简牍博物馆地下室及其基础的影响，采用排桩结构进行支护.为了进一步验证本文方法的工程实用价值，现对该项目进行计算，同时分析土压力变化控制参数c1，c2对计算结果的影响.计算参数如下：基坑周围土体重度γ=19kN/m3，内摩擦角φ=30°，粘聚力c=12 kPa；桩径为d=1.2 m，桩身钢筋混凝土弹性模量为24×106kPa，基坑开挖深度H1=6 m，桩身嵌固深度H2=7 m.为便于分析，采用两种方式进行计算：一是考虑参数c1变化，而c2取定值的情况；二是考虑参数c2变化，而c1取定值的情况.以下分别就两种情况进行讨论．

1)考虑c1变化，c2为定值的情况.

由图4(a)可以看出，当c1逐渐增大，桩身水平位移逐渐减小．这是因为c1越大，基坑外侧土压力随桩身位移增大减小的速度越快，桩身所受主动荷载减小.由图4(b)和(c)可以看出，基坑外侧土压力随深度逐渐增大，在桩底附近增大速度加快，而基坑内侧土压力随深度逐渐增大，至某一深度后逐渐减小.由图4(d)和(e)可以看出，c1改变不影响桩身剪力和弯矩的分布模式，最大剪力和弯矩出现的位置不变，但最大剪力和弯矩的绝对值均随c1增大而减小.

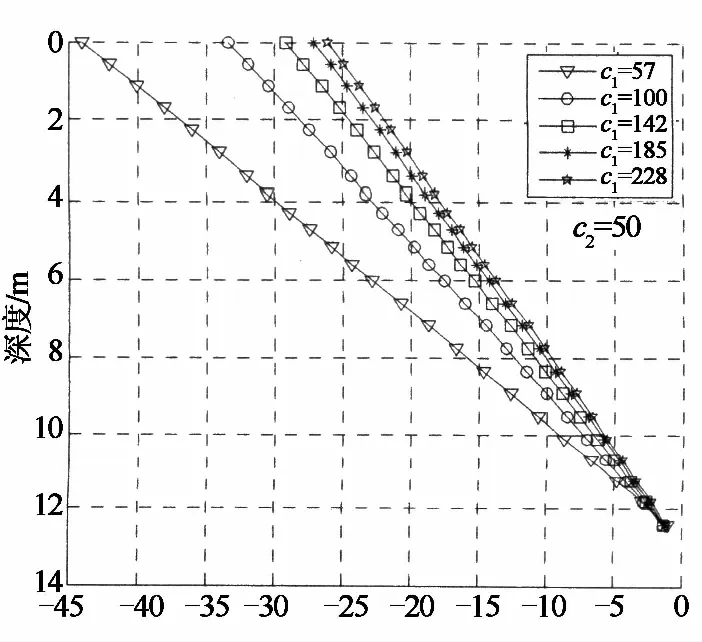
水平位移/mm(a)

基坑外侧土压力/kPa(b)

基坑内侧土压力/kPa(c)

剪力/kN(d)

弯矩/(kN·m)(e)图4 c1变化，c2为定值的计算结果Fig.4 Calculation results for the case of c1 varying and c2 setting to a constant

2)考虑c2变化，c1为定值的情况.

由图5(a)可以看出，随着c2逐渐增大，桩身的水平位移逐渐减小．这是因为c2越大，基坑内侧土体被动抗力充分发挥所需的桩身位移越小，所以桩身侧向位移的发展受到更大的限制.由图5(b)和(c)可以看出，基坑内、外侧土压力随深度变化的规律与图4(b)和(c)所揭示规律一致，但在同一深度处，基坑内、外侧土压力随c2变化的规律与图4(b)和(c)中随c1变化的规律相反.将图5(d)和(e)与图4(d)和(e)进行对比可以发现，c2对桩身剪力和弯矩的分布模式也没有明显影响，但最大剪力和弯矩的绝对值随c2增大而逐渐增大.

水平位移/mm(a)

基坑外侧土压力/kPa(b)

基坑内侧土压力/kPa(c)

剪力/kN(d)

弯矩/(kN·m)(e)图5 c2变化，c1为定值的计算结果Fig.5 Calculation results for the case of c2 varying and c1 setting to a constant

从以上的分析结果可以看出，土压力变化控制参数c1,c2可以调节基坑内、外侧土压力随桩身位移变化的规律，其对计算结果的影响主要表现为对桩身侧向位移大小和最大剪力、弯矩值的影响，而对桩身位移和内力的分布形式的影响较小.总体而言，参数c1,c2在其取值范围内变化时，计算结果的变化较为平缓，因此实际计算中不会出现因参数取值的偏差而造成计算结果误差很大的情况.另外，从计算结果还可看出，由于悬臂式排桩没有设置锚杆或内支撑，因此其桩顶处的侧向位移值相对较大；桩底附近由于桩身侧向位移方向的改变，基坑外侧土压力迅速增大，基坑内侧土压力迅速减小.该结果表明，通过将基坑内、外侧土压力的变化与桩身侧向位移的变化联系起来，本文方法较好地考虑了桩-土之间的相互作用机理，因而能较好地反映悬臂式排桩的实际受力情况.

4 结 论

桩-土间的相互作用是悬臂式排桩内力计算的关键因素.本文引入非线性的桩-土相互作用模型，提出了一种可考虑桩-土相互作用机理的悬臂式排桩内力计算方法，通过实际工程应用，可得出以下结论．

1)采用有限单元法建立结构刚度方程，并采用Newton-Raphson法进行迭代求解，可以快速计算出结构位移列阵，从而避免了共同变形理论中对结构位移进行不断调整的繁琐过程，极大地提高了求解效率.

2)通过假定基坑内、外侧土压力与桩身侧向位移间的非线性函数关系，较好地考虑了桩-土间的相互作用机理和土压力变化非线性的特点.

3)从影响因素分析的结果来看，参数c1,c2可以调整土压力随桩身侧向位移的变化规律，在给定的取值范围内，计算结果变化较为平缓，因此实际计算时不会出现因参数取值的偏差而造成计算误差很大的情况，本文方法适合于工程应用.

[1] 刘国彬, 王卫东. 基坑工程手册[M]. 第二版. 北京: 中国建筑工业出版社, 2009.

LIU Guo-bin, WANG Wei-dong. Excavation engineering manual [M]. Second Edition. Beijing: China Architecture and Building Press, 2009. (In Chinese)

[2] 高大钊, 孙均. 深基坑工程 [M]. 第二版.北京: 机械工业出版社, 2002.

GAO Da-zhao, SUN Jun. Deep excavation engineering [M]. Second Edition. Beijing: China Machine Press, 2002. (In Chinese)

[3] 赵其华. 岩土支挡与锚固工程[M]. 成都: 四川大学出版社, 2008.

ZHAO Qi-hua. Retaining and anchor engineering for rock and soil mass[M]. Chengdu: Sichuan University Press, 2008. (In Chinese)

[4] 杨斌, 胡立强. 挡土结构侧土压力与水平位移关系的试验研究[J]. 建筑科学, 2000, 16(2): 14-20.

YANG Bin, HU Li-qiang. Test study on relationship between lateral earth pressure acting on retaining structures and horizontal displacement[J]. Building Science, 2000, 16(2): 14-20. (In Chinese)

[5] 张永兴, 陈林. 挡土墙非极限状态主动土压力分布[J]. 土木工程学报, 2011, 44(4): 112-118.

ZHANG Yong-xing, CHEN Lin. Active earth pressure on retaining walls in non-limit state[J]. China Civil Engineering Journal, 2011, 44(4): 112-118. (In Chinese)

[6] 应宏伟, 谢康和, 潘秋元, 等. 土与变形完全耦合的挡土结构分析方法[J]. 土木工程学报, 2000, 33(2): 96-100.

YIN Hong-wei, XIE Kang-he, PAN Qiu-yuan,etal. Method of analyzing retaining structure considering earth pressure fully coupled with deformation[J]. China Civil Engineering Journal, 2000, 33(2): 96-100. (In Chinese)

[7] 邓子胜, 邹银生, 王贻荪. 考虑位移非线性影响的深基坑土压力计算模型研究[J]. 工程力学, 2004, 21(1): 107-111.

DENG Zi-sheng, ZOU Yin-sheng, WANG Yi-sun. Calculation of the earth pressure considering nonlinear displacement influence on deep excavation[J]. Engineering Mechanics, 2004, 21(1): 107-111.(In Chinese)

[8] 崔允亮. 水平荷载作用下排桩受力和变形研究[D]. 扬州: 扬州大学建筑科学与工程学院, 2009.

CUI Yun-liang. Research on the mechanical and deformation characteristics of row piles under horizontal loads[D]. Yangzhou:College of Architectural Science and Engineering, Yangzhou University, 2009. (In Chinese)

[9] 王元战, 李蔚, 黄长虹. 墙体绕基础转动情况下挡土墙主动土压力分布[J]. 岩土工程学报, 2003, 25(2): 208-211.

WANG Yuan-zhan, LI Wei, HUANG Chang-hong. Distribution of active earth pressure with wall movement of rotation about base[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(2): 208-211. (In Chinese)

[10] 李永刚. 挡土墙被动土压力研究[J]. 岩土力学, 2003, 24(2): 273-276.

LI Yong-gang. Study on passive earth pressure of retaining wall[J]. Rock and Soil Mechanics, 2003, 24(2): 273-276. (In Chinese)

[11] LEE S H, KIM S I, LEE J H,etal. Two-parameter beam-column model and back analysis for flexible retaining walls[J]. Computers and Geotechnics, 2004, 31(6): 457-472.

[12] FINNO R J, HARAHAP I S, SABATINI P J. Analysis of braced excavations with coupled finite element formulations[J]. Computers and Geotechnics, 1991, 12(2): 91-114.

[13] WHITTLE A J, HASHASH Y M A, WHITEMAN R V. Analysis of deep excavation in Boston [J]. Journal of Geotechnical and Geoenvironmental, ASCE, 1993, 119(1): 60-90.

[14] TERZAGHI K, PECK R B. Soil mechanics in engineering practice[M]. New York: John Wiley, 1967.

[15] 郑成德.数值计算方法[M]. 北京: 清华大学出版社, 2010.

ZHENG Cheng-de. Numerical computation method[M]. Beijing: Tsinghua University Press, 2010. (In Chinese)

[16] 赵明华. 土力学与基础工程[M]. 武汉: 武汉理工大学出版社, 2000:272-295．

ZHAO Ming-hua. Soil Mechanics and foundation engineering[M]. Wuhan: Wuhan University of Technology Press, 2000:272-295. (In Chinese)