基于LIBSVM和智能算法的电站锅炉飞灰含碳量优化
卢洪波,王金龙
(东北电力大学能源与动力工程学院,吉林 吉林 132012)
煤粉在锅炉内的燃烧是个复杂的物理化学过程,各种因素相互影响相互制约,飞灰含碳量是反映炉内燃烧过程好坏的重要指标,对于电厂锅炉的安全经济运行有重要影响[1]。影响飞灰含碳量的因素很多而且复杂,预测和控制都比较困难。电站锅炉实际运行时依据经验和有限的调试结果难以将实炉的燃烧工况调整到最佳状态下,因此对飞灰含碳量建立适当的模型并对其进行控制和优化是有重要意义的。
燃煤电站锅炉飞灰含碳量偏高的原因有很多而且复杂,其主要受煤粉细度、煤种特性、燃烧器的结构特性、热风温度、炉内空气动力场和锅炉负荷等因素的影响[2]。如何调控这些影响因素使飞灰含碳量达到理想的数值成为多数学者的研究课题。由于锅炉内的燃烧过程是非线性的,各种因素相互耦合,用常规的理论研究方法难以进行。利用神经网络对锅炉燃烧过程进行非线性建模,并运用遗传优化算法对飞灰含碳量进行优化成为降低锅炉飞灰含碳量的主要研究方法[3-9]。然而,随着近年来人工智能算法的发展,运用改进的支持向量机算法对锅炉燃烧系统进行建模相比于神经网络模型要更精确,训练时间短,泛化能力强[10-12]。而且遗传算法的优化效果相比其他智能算法如粒子群算法、微分进化算法等并不是那么理想,寻优速度慢,泛化能力差,极易陷入局部最优值。
王春林、周昊和周樟华等人应用支持向量机建立了大型电站燃煤锅炉的飞灰含碳量特性模型并利用飞灰含碳量的热态实炉试验的数据对模型进行了校验,对飞灰含碳量进行了优化,结果表明支持向量机是锅炉飞灰含碳量特性建模的有效工具[13]。周建新、王雷和徐治皋等人借助锅炉燃烧特性实验结果,建立了基于支持向量回归的电站锅炉飞灰含碳量模型,并对模型进行了校验,结合全局寻优的遗传算法对锅炉飞灰含碳量进行了优化并获得了具体工况下的最佳操作参数[14]。李钧、阎维平和李春等人对某电厂300 mw四角切圆煤粉锅炉飞灰含碳量排放特性进行了数值模拟,以数值计算结果为样本,建立了基于支持向量机的四角切圆燃烧锅炉飞灰含碳量预测模型,模型预测结果与数值模拟结果最小相对误差为1.01%,说明基于支持向量机算法的四角切圆煤粉锅炉飞灰含碳量模型能够较好地对锅炉飞灰可燃物含量进行预测[15]。综上所述,目前支持向量机已经成为统计分类、预测、非线性建模等领域的重要研究手段。
本文利用一种改进的支持向量机算法(LIBSVM)建立了大型电站燃煤锅炉飞灰含碳量特性的模型,并对该模型进行了训练和校验,结果表明所建模型能够根据相关运行参数的调整准确预测锅炉在不同工况下的飞灰含碳量特性,计算速度快,并具有良好的泛化性,结合相关人工智能算法进行寻优,可为大型电站锅炉燃烧调整提高锅炉运行的安全性与经济性提供有效的手段。
1 用于解决非线性回归问题的支持向量机算法简介
对于分类问题支持向量机采用最优分类面的方法,将分类问题转化为一个凸二次规划问题,并应用拉格朗日函数求解。对于回归问题支持向量机在引入精度ε后就可以应用分类问题的方法。假设给定了训练数据集 S={(xi,yi),i=1,2,3…m,xi∈Rd,yi∈R,R为实数集,Rd为d维空间集},支持向量机首先通过非线性映射φ:Rd→Rn,将输入向量x映射到高维线性特征空间上并在该空间内进行线性回归,回归方程为:

考虑到会有样本点在目标函数的ε精度之外,引入松弛因子ξi≥0,这时回归问题就转化为最小化结构风险函数的问题,即:

式(2)中第一项是使回归函数更为平坦,泛化能力更好,第二项则为减少误差,常数C>0为罚系数,控制对超出误差e的样本的惩罚程度。f(xi)与yi的差别小于ε时误差计为 f(xi)-yi-ε。
可以利用拉格朗日乘子法来求解最优化问题:

详见参考文献[16]
2 超临界锅炉飞灰含碳量的支持向量机模型

图1 飞灰含碳量的支持向量机模型图
超临界锅炉飞灰含碳量的支持向量机模型,如图1所示。模型输入参数的选取如下:负荷是锅炉的基本参数,表征了给水流量及总燃料量等值,应作为模型的输入。一次风粉的配比方式直接影响着炉膛的空气动力场和燃烧气氛,使机械未完全燃烧热损失和化学未完全燃烧热损失发生变化,直接影响着飞灰含碳量的大小,所以选择各磨煤机出口的一次风量和给煤量来表征同一层燃烧器的风粉比。煤粉细度是煤燃烬的重要参数,煤粉颗粒越细,碳粒的比表面积就越大,有利于提高碳粒的燃烧速度,降低飞灰含碳量,由于机组磨煤机采用动态煤粉分离器调节煤粉细度,故选择磨煤机动态分离器电机转速和磨煤机电机电流和各磨给煤量来表征煤粉细度对飞灰含碳量的影响。二次风、燃尽风的配比及总风量对煤粉的燃烧状况有较大的影响,故选择前后墙二次风开度、二次风量和烟气含氧量作为模型的输入。一、二次风温直接影响煤粉的着火及燃尽,风温高可以减少煤粉着火所需的热量,有利于煤粉的着火和燃尽,故选择一、二次风温作为模型的输入参数。考虑到电厂用煤在一段时间内不会改变,所以不将煤质因素考虑在内。综合上述分析,将以上因素作为模型的输入参数,以飞灰含碳量为输出参数建立模型。
核函数的选择对于支持向量机回归分析具有一定的影响,较常用的核函数有:径向基函数、多项式函数、Sigmoid函数、线性函数等,径向基函数相比其他核函数效果要更好些[17],因此本文选择径向基函数 f(x)=ae-(x-b)2/c2作为核函数。
分别取前45组数据作为训练样本,后31组数据作为验证样本,对支持向量机模型进行训练和验证,采用径向基核函数进行回归分析,并应用选择好的参数对工况1进行预测。模型的不敏感损失函数参数e取为10-3,设定当训练误差小于10-5时停止训练,拉格朗日乘子上界C取为100,宽度width取为3。经训练和验证后,训练样本的均方误差为0.41%,验证样本的均方误差为0.92%。
图2为训练样本飞灰含碳量计算值与实际值的比较:
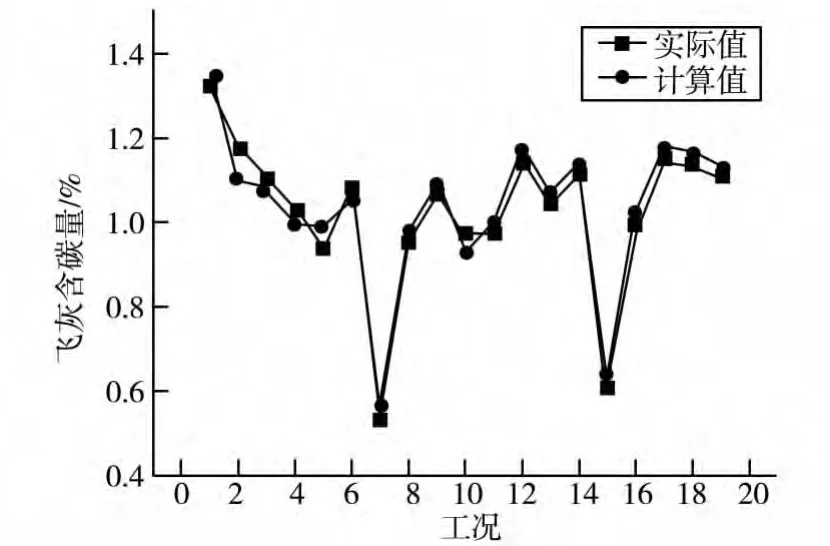
图2 训练样本飞灰含碳量计算值与实际值对比图

图3 验证样本的相对误差曲线图
从图中可以看出,飞灰含碳量的计算输出与实际输出非常接近,说明该模型能够正确的反映出输入量与输出量之间的非线性关系,能够应用于实际的工程预测。
验证样本的最大相对误差为1.95%,平均相对误差为0.92%,满足工程实际要求。
图3为验证样本的相对误差曲线图:红色线为现场的实际运行数据,蓝色线为模型的计算数据,从图中可以看出,除个别点误差相对大一点外,其他各个工况的模型计算数据与现场的实际运行数据非常稳合,说明该模型能够模拟锅炉内复杂的燃烧过程。
3 基于人工智能算法的锅炉飞灰含碳量优化
应用支持向量机建模的目的是为了对系统进行优化,即以飞灰含碳量为目标,在保证锅炉出力和安全运行的前提下调整燃烧工况的可调参数,使飞灰含碳量达到最优值。定义优化目标为:

式中:f表示由已训练好的支持向量机所建立的映射关系。f可以表述为:

式中:f为飞灰含碳量;xi为支持向量机输入层第i个变量;Xl为支持向量机训练样本;Ei为第i个输入变量的取值范围;δ为核函数;i=1,2,3……19,a、b分别为支持向量机的拉格朗日乘子和偏差量[18]。
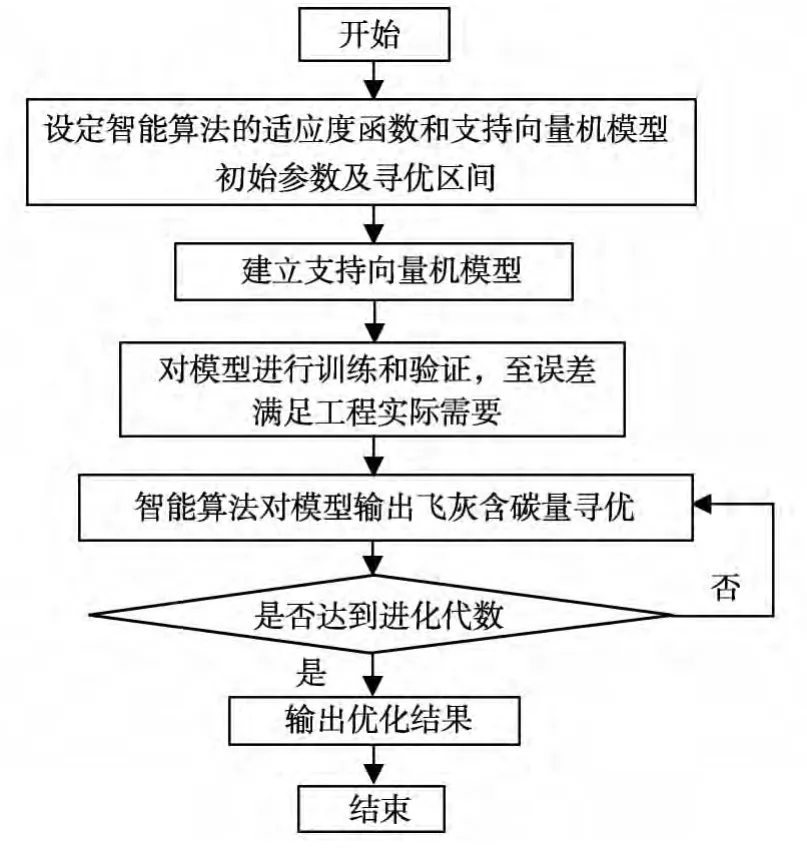
图4 智能算法寻优流程图
样本归一时有最大值和最小值,寻优范围就在最大值和最小值的基础上分别加减10%,针对飞灰含碳量较高工况4进行优化。为了保证负荷稳定,给水温度不宜过低,故在优化时限定给水温度的取值范围为257℃ ~296℃。
利用人工智能算法进行飞灰含碳量优化,在模拟锅炉排放上得到了广泛的应用。初始化种群规模为20,最大进化代数为50,优化函数选择高斯函数,寻优流程见图4。
经过计算后优化飞灰含碳量至0.97%。同时得到了该工况下的运行参数调整情况如表1所示,从表中可以看出,对于此优化工况,运用遗传算法优化后的飞灰含碳量值为1.09%,相比原始值降低了0.11%,然而运用粒子群算法和微分进化算法优化后的飞灰含碳量值为0.97%,相比原始值降低了0.23%,后两种方法相比于遗传算法优化效果更好。同时得到了相应的参数调整策略,提高中层、上层和燃尽风门的二次风量,可以使在燃烧器底层未燃尽的碳在随烟气上升的过程中,有足够的氧气与其接触燃烧,从而降低烟气中的飞灰含碳量。在此基础上,降低烟气含氧量,提高二次风量和二次风温也能很好的降低飞灰含碳量。

表1
图5分别是三种优化方法对飞灰含碳量的寻优过程图。
从图中可以看出,遗传算法的寻优过程曲线比较平缓,达到最大进化代数时的寻优结果为1.09%,寻优过程耗时比较长,优化结果不理想,不适合在线优化。然而,粒子群算法和微分进化算法的寻优过程曲线前期下降非常明显,在进化代数达到38代左右时,即寻得最优飞灰含碳量,速度非常快,非常适合在线进行优化,从图中不难看出,相比于粒子群算法,微分进化算法的优化效果要更好,寻优曲线趋于稳定的过程更快,如果用于在线优化,微分进化算法是不错的选择。

图5 GA、PSO、DE算法的寻优过程图
4 结 论
超临界电站煤粉锅炉的飞灰含碳量受到多种因素的影响,而且影响关系非常复杂,飞灰含碳量的预测和控制都比较困难,本文采用LIB支持向量机的方法建立了飞灰含碳量的预测模型并应用现场的运行数据对该模型进行了训练和验证,误差表明该模型对飞灰含碳量的预测具有很好的效果。在此基础上,运用遗传算法、粒子群算法和微分进化算法分别对飞灰含碳量进行了优化,优化后的飞灰含碳量相比于原始值降低了0.23%,减少了飞灰带走的热损失,同时得到了相应的输入变量的参数调整范围,对于指导电厂的安全经济运行具有一定的应用价值。
[1]陈彪,丁艳军,吴占松.670t/h煤粉炉飞灰含碳量的神经网络预测建模[J].电站系统工程,2005,21(6):17-22.
[2]叶学民,彭波.燃煤电站锅炉飞灰含碳量偏高的原因分析及解决措施[J].锅炉技术,2004,35(3):49-51.
[3]方湘涛,叶念渝.基于BP神经网络的电厂锅炉飞灰含碳量预测[J].华中科技大学学报:自然科学版,2003,31(12):75-77.
[4]赵新木,王承亮,吕俊复,岳光溪.基于BP神经网络的煤粉锅炉飞灰含碳量研究[J].热能动力工程,2005,20(2):158-162.
[5]陈敏生,刘定平.电站锅炉飞灰含碳量的优化控制[J].动力工程,2005,25(4):545-549.
[6]张毅,丁艳军,张鸿泉,等.电站锅炉运行性能综合预测模型[J].动力工程,2006,26(1):84-88.
[7]温文杰,马晓茜,刘翱.锅炉混煤掺烧的飞灰含碳量预测与运行优化[J].热力发电,2010,29(3):30-35.
[8]刘定平,陈敏生,马晓茜.基于HGA-ANN配风方式的锅炉飞灰含碳量优化[J].华南理工大学学报:自然科学版,2006,34(4):96-100.
[9]陈敏生,刘定平.基于遗传神经网络和群体复合形法的配风方式对锅炉飞灰含碳量影响研究[J].锅炉技术,2006,37(3):9-14.
[10]赵显桥,吴胜杰,何国亮,等.支持向量机灰熔点预测模型研究[J].热能动力工程,2011,26(4):436-439.
[11]顾燕萍,赵文杰,吴占松.基于最小二乘支持向量机的电站锅炉燃烧优化[J].中国电机工程学报,2010,30(17):91-97.
[12]蔡杰进,马晓茜.基于SVM的燃煤电站锅炉飞灰含碳量预测[J].燃烧科学与技术,2006,12(4):312-317.
[13]王春林,周昊,周樟华,等.基于支持向量机的大型电厂锅炉飞灰含碳量建模[J].中国电机工程学报,2005,25(20):72-76.
[14]周建新,王雷,徐治皋,司风琪.大型电站锅炉飞灰含碳量优化模型研究[J].锅炉技术,2008,39(3):21-24.
[15]李钧,阎维平,李春,等.基于预数值计算的锅炉飞灰可燃物含量建模[J].中国电机工程学报,2009,29(17):32-37.
[16]徐志明,赵永萍,文孝强,孟硕.基于退火支持向量的燃煤锅炉结渣特性预测[J].热能动力工程,2011,26(4):440-444.
[17]费洪晓,黄勤径,戴戈,肖新华.基于SVM与遗传算法的燃煤锅炉燃烧多目标优化系统[J].计算机应用研究,2008,25(3):811-813.
[18]刘定平,蔡泓铭,叶向荣.基于LSSVM-MODE的锅炉效率与NOx排放优化研究[J].热力发电,2010,39(7):23-26.

