风力机组关键部件运动学与动力学仿真研究
张光辉
(中色科技股份有限公司, 河南 洛阳 471003)
风力机组关键部件运动学与动力学仿真研究
张光辉
(中色科技股份有限公司, 河南 洛阳471003)
以风力发电机组为研究对象,采用动量叶素理论计算叶片在不同风速下的气动载荷,在三维软件Solidworks中建立了叶片、轮毂、机舱和塔架等关键功能部件的三维模型,在Ansys中对叶片和塔架进行柔性化处理,生成叶片和塔架的MNF文件,建立了风力机组关键功能部件的ADAMS刚柔耦合多体系统动力学模型.将计算的载荷均匀加载到风力机组的叶片上,对风力机在风速由5m/s变化到25m/s的过程进行仿真,得到叶片和塔架的振动变形特性曲线.该仿真能够很好地模拟风力机的振动变形特性,为风力机的虚拟样机仿真提供了一种可行的方法.
风力发电机组; 动量叶素理论; 刚柔耦合; 运动学与动力学分析; 仿真
0 前 言
水平轴风力发电机系统是一个非线性流刚柔耦合的多体动力学系统,机械结构和运动规律非常复杂.在建立动力学模型时,必须考虑叶片的几何非线性和大变形运动,机舱偏航过程的刚体运动,塔架的弹性变形,以及复杂多变的气动载荷等因素的影响.水平轴风力机的叶片作为弹性体,在运行过程中受到气动载荷、弹性力、离心力和重力的作用,这些力耦合在一起会引起不稳定的振动,这种不稳定振动是导致叶片破坏的重要原因之一.因此,叶片的气弹稳定性问题一直是人们关注的焦点.在风轮旋转的过程中,塔架顶端会受到来自风轮的周期性激励和气动载荷的影响,这种激励会引起塔架的前后振动,塔架的振动和叶片的振动耦合到一起,往往会导致风力机组的破坏.因此,研究风力发电机组的振动变形特性非常必要.本文建立了风力机组关键功能部件的刚柔耦合动力学模型,通过仿真得到叶片和塔架的振动变形特性曲线,为风力机运动学和动力学仿真研究进行了一次有益的探索.
1 叶片气动载荷计算
动量叶素理论假设作用于叶素上的力仅和通过叶素扫过圆环的气体的动量变化有关,可以通过用微元截面上入射合速度攻角的二维翼型特性计算得出.因此,可以假定邻近圆环的气流之间不发生径向干涉作用,忽略顺叶片展向的速度分量和三维效应.在叶片的某一径向位置上的气流速度分量用风速来表示,知道攻角和升、阻系数以及每个叶素上的轴、切向诱导因子,最终求出在一定风速下作用在叶素上的气动载荷[1].
设风轮旋转角速度为Ω、叶素弦长为L,浆距角为β,考虑半径r处展向长度为δr的叶素,其切向速度为Ωr,相应的尾流切向速度分量为α′Ωr,当风速v∞作用于其上时,两者形成的合成速度为:
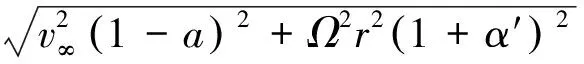
(1)
式中:a为垂直风轮旋转平面的轴向气流诱导因子;α′为切向气流速度诱导因子.
叶素界面处气流速度的几何关系如图1所示.

图1 叶素界面处气流速度的几何关系Fig.1 Geometric relation of air velocity around blade element interface
气流作用在叶素上产生的升力和阻力如图2所示.当气流流经翼型表面时,将产生垂直于气流方向的生力dFL和平行于气流方向的阻力dFD.
作用在翼型表面的升力dFL和阻力dFD为:

(2)

(3)
式中:W为气流对叶素的相对速度;ρ为空气密度;L为距转轴r处的翼型弦长;CL、CD分别为升力系数和阻力系数,该值有所选翼型决定.
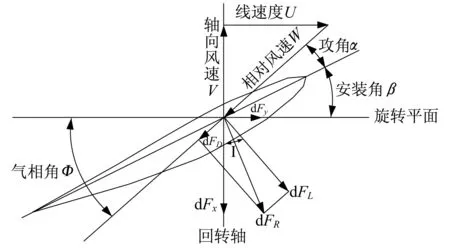
图2 作用在叶片上的升力和阻力Fig.2 Lift and drag upon blade
把风轮旋转平面作为参考平面,将dFL和dFD分别投影到转轴和圆周速度上如图3所示.

图3 叶素气动力的法向分量和切向分量Fig.3 Normal component and tangential component of blade aerodynamic force
作用在风轮半径r处,宽度为δr叶素上的气动力法向分量为
(4)
作用在风轮半径r处,宽度为δr叶素上的气动力切向分量为
(5)
为了计算叶素微元上的气动载荷,必须计算风轮旋转面中的轴向诱导因子α和切向诱导因子α′.α和α′可通过下面两式迭代求得.
(6)
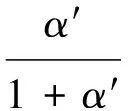
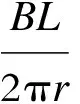
根据动量叶素理论,将叶片模型沿展向分成12个叶素微元,在Matlab中编程计算得到叶片分别在风速为5,10,15,20和25 m/s时受到的气动载荷.各种风速下的气动载荷的大小和变化趋势如图4所示.
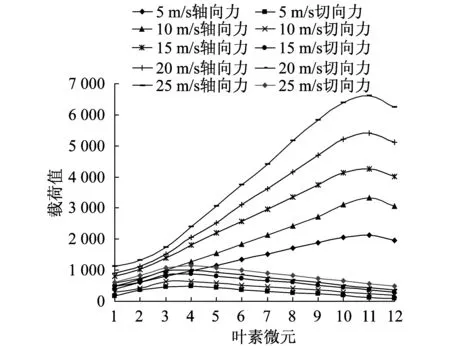
图4 载荷大小和变化趋势Fig.4 Trend of magnitude of load and variation
2 风力机关键部件仿真模型的建立
2.1 风力机组关键的三维建模
风力发电机组主要由叶片、塔架、机舱和塔架等关键部件组成,本文选取了叶片的技术参数,采用NACA系列翼型对叶片进行建模,通过坐标变换把翼型数据转换到相应叶素截面的三维空间坐标,生成叶素截面曲线,然后沿导引线扫描生成叶片的三维实体模型,实现了叶片的精确建模[2].根据仿真的需要,对风力机组的其他结构进行了相应的简化,完成整机关键功能部件的三维模型的建模,在Solidworks装配环境下进行装配,为后面的仿真打下了基础.图5为风力发电机组的三维模型.

图5 风力发电机三维模型Fig.5 Wind turbine’s 3D model
2.2 刚柔耦合模型的建立
把在Solidworks建立的三维模型通过接口导入到ADAMS中,通过添加材料属性和约束建立风力机组关键部件的多刚体动力学模型.在风机实际运行过程中,叶片和塔架的变形比较大,需要对叶片和塔架进行柔性化处理.因此,必须对叶片和塔架进行模态分析,然后生成叶片和塔架的模态中性文件,最后导入到ADAMS中替换掉原刚体,进行刚柔耦合,才能进行关键部件的柔性多体动力学分析[3-4].
叶片和塔架的模态分析在有限元分析软件Ansys中进行,主要是求得叶片和塔架的各阶固有频率和振型,结果见表1.
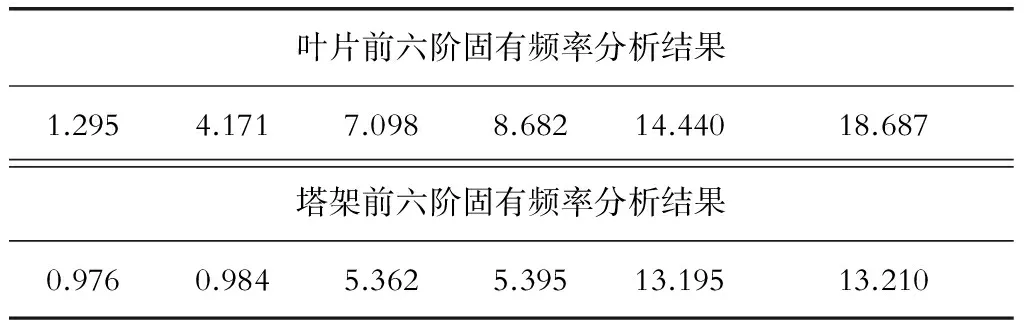
表1 叶片和塔架的固有频率分析结果Tab.1 Analysis result of blade and nacelle’s natural frequency
将前面分析得到的叶片的塔架的MNF文件导入到ADAMS中,替换掉原刚体,最终生成的刚柔耦合多体系统动力学模型如图6所示[5-8].
2.3 气动载荷的加载
前面计算得到的气动载荷仅仅是几种不同风速下的气动载荷.用STEP函数将载荷按风速由5 m/s变化到25 m/s的过程均匀加载到叶片上,STEP函数为三次样条曲线,这样能够比较理想地反应叶片上气动载荷实际的变化过程[9].气动载荷加载后的模型如图7所示.

图6 刚柔耦合模型Fig.6 Rigid-flexible coupling model
图7 加载后的动力学模型Fig.7 Dynamical model after reload
3 仿真结果分析
以上述建好的风力发电机组关键功能部件刚柔耦合多体系统动力学模型为对象,在风向恒定的情况下,当叶轮转速为16 r/min时,对风速从5 m/s均匀变化到25 m/s的过程进行仿真,得到叶片和塔架的运动学与动力学特性的变化情况[10-11].仿真结果如图8所示.
风力发电机组的叶片和塔架都是柔性体,在运行过程中,气动载荷、弹性力、重力和离心力之间相互耦合,因此变形过程是一个气弹耦合过程,表现在叶片尖部和塔架顶部的变形是振荡的. 由上面的仿真分析结果可以看出,在风速逐渐增大的过程中,叶片尖部的振动变形较大,叶片中部的振动变形较小,塔架顶端的振动变形相对更小.由于阻尼的存在,叶片尖部和中部的位移、速度和加速度是周期性衰减变化的,叶片尖部的变形量趋于稳定值2.3 m,变形速度趋于0.5 m/s,变形加速度趋于20 m/s2;由于塔架本身的刚度较大,振动变形相对叶片来说是很小的,塔架顶端的变形趋于0.062 m,变形速度趋于0.04 m/s,变形加速度趋于0.27 m/s2;有叶片的最大变形可知,风轮在旋转过程中不会与塔架发生干涉,这说明整机的气动弹性是良好的.
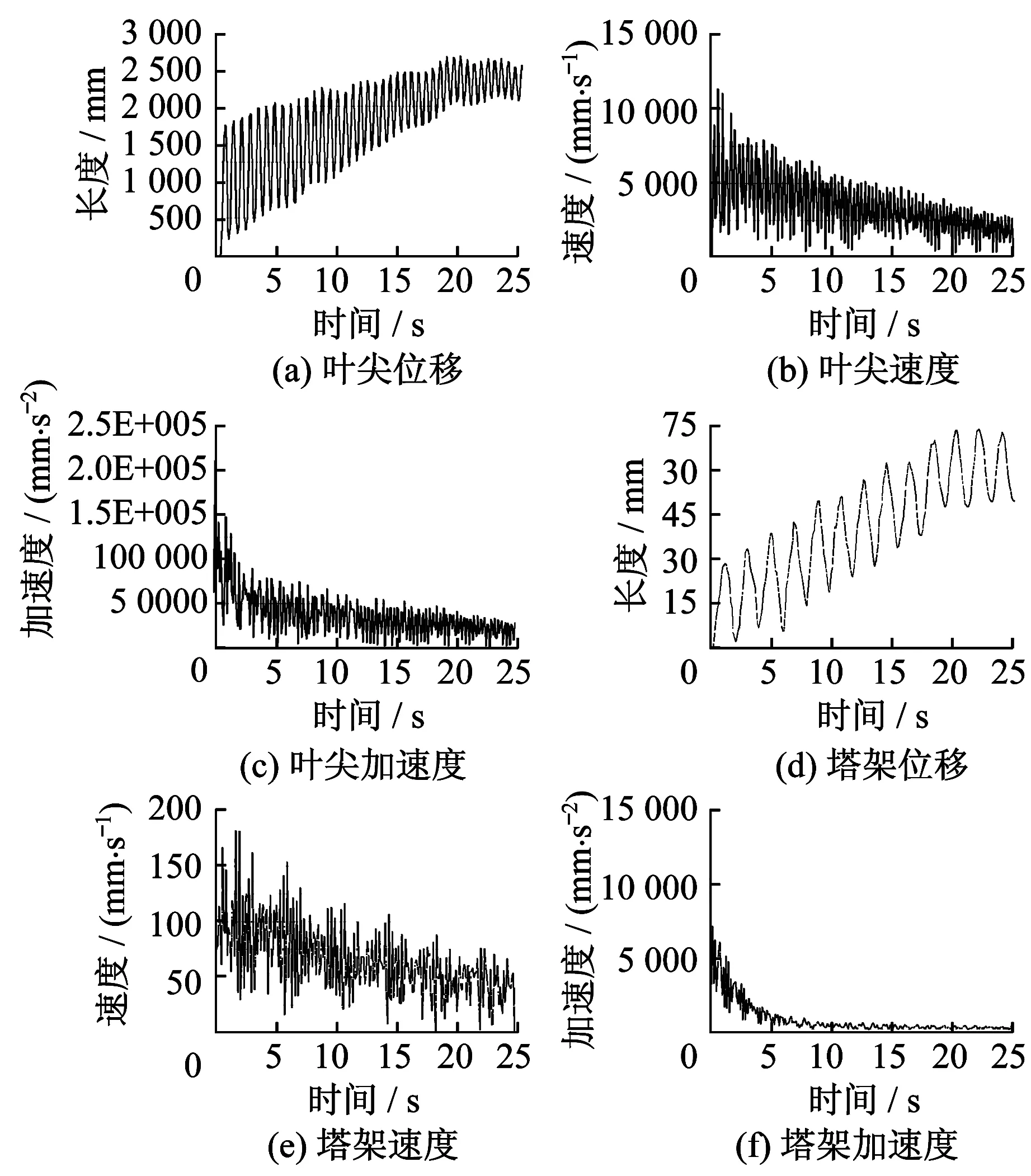
图8 仿真结果Fig.8 Results of simulation
4 结 论
本文以风力发电机组关键部件的刚柔耦合动力学模型为研究对象,对风速由5~25 m/s的变化过程进行了仿真,得到了叶片和塔架的振动变形特性曲线,对风力机的振动特性进行了一次有益的探索,并得到以下结论:
(1) 叶片作为一个柔性体,在风机运行过程中,叶尖部位的位移、变形速度和加速度都是很大的,振动变形过程比较剧烈.叶片的振动变形过程是气动载荷、弹性力、重力和离心力相互耦合的结果.
(2) 由于风轮的旋转平面和竖直面有一定的夹角,风轮旋转过程中叶片的重力和气动载荷给塔架的顶部一个周期性的激励,因此塔架顶部的位移、速度和加速度也是周期性变化的.塔架本身的刚度较大,所以和叶片的振动变形相比,塔架的振动变形比较小.
[1]赵锋,段巍.基于叶素-动量理论及有限元方法的风力机叶片载荷分析和强度分析[J].机械设计及制造,2010(8):42-44.
[2]王学永.风力发电机叶片设计及三维建模[D].北京:华北电力大学,2008.
[3]王磊,杜静.刚柔耦合技术在摩托车动强度分析中的应用[C]∥天津内燃机研究所.2008中小型内燃机专业技术研讨会论文集.天津:2008:25-28.
[4]崔荫.汽轮机旋转叶片刚柔耦合系统的动力学问题研究[D].哈尔滨:哈尔滨工程大学,2008.
[5]Asseff N S,Mahfuz H.Design and finite element analysis of an ocean current turbine blade[J].GlobalandLocalChallenges,2009,10.
[6]王应军,裴鹏宇.风力发电机叶片固有振动特性的有限元分析[J].华中科技大学学报,2006,23(2):44-46.
[7]Mohammad AIHamaydeh,Saif Hussain.Optimized frequence-based foundation design for wind turbine towers utilizing soil-structure interaction[J].JournalofTheFranklinInstitute,2010,4.
[8]王朝胜.基于有限元法的风力发电机组塔架结构分析[D].长沙:长沙理工大学,2010.
[9]邵金华.风力发电机系统动力特性仿真研究[D].重庆:重庆大学,2007.
[10]Wang J H,Qin D T,Lim T C.Dynamic analysis of horizontal axis wind turbine by thin-walled beam theory[J].JournalofSoundandVibration,2010,329:3565-3586.[11]张锁怀,张文礼,张青雷.基于Adams的MW级风力发电机组动力学建模[J].华北电力大学学报,2009,36(4):51-57.
TheKinematicandDynamicSimulationofKeyFunctionalComponentsof
WTGSZHANGGuang-hui
(ChinaNonferrousMetalsProcessingTechnologyCo.,Ltd.,Luoyang471039,China)
In the article,the blade element momentum theory was used for the calculation of aerodynamic load of blade under the different wind velocities.A 3D model of key functional components such as blade,tower,hub and nacelle were modeled in Solidworks,the MNF files of blade and tower were gained in finite element analysis software after flexible processing,and the rigid-flexible multi-body dynamic model of the wind turbine’s key components was created in ADAMS.Through the simulation of the model under constant rotate speed,kinematic and dynamic curves were obtained while the wind speed rose from 5 m/s to 25 m/s.This simulation imitates the vibration performance ideally,which provides a feasible method for the virtual prototype simulation of wind turbines.
wind turbine; blade element momentum theory; rigid-flexible coupling; kinematic and dynamic analysis; simulation
2014-05-10
张光辉(1984-),男,工程师,主要从事有色金属压力加工设备的设计工作.E-mail:guanghui0379@163.com
TM315
A

