负向等谱4位势Ablowitz-Ladik方程的类有理解

程 瑜

(徐州工程学院 数学与物理科学学院, 江苏 徐州 221111)

0 引言

作为孤立子理论中的热门课题，孤子方程的精确解及其性质长期以来受到学者的关注.随着研究的深入，很多有效寻求孤子方程精确解的办法被提出,其中，Wonskian技巧[1-2]是一种以Hirota双线性方法为基础，求解具有双线性形式的孤子方程的直接且高效的方法.双Wronskian是Wronskian技巧的一种推广[3]，被用来构造双Wronski行列式解[4].在离散系统中，双Wronskian解又被称为双Casoratian解[5-6].孤子解、有理解等多种形式的精确解都可用Wronskian行列式形式表示.Nimmo和Freeman根据文献[7]中提出的长波求极限的观点首次给出了KdV方程的有理解的Wronskian形式[8].基于此，张大军等[9-10]研究了Toda链和微分-差分KdV方程的有理解等.陈登远等在此基础上将Wronskian行列式元素满足的下三角方程推广到任意的矩阵方程,得到AKNS方程的新Wronski解，通过将矩阵取成不同的形式，给出Wronskian行列式形式的孤子解、有理解等多种形式的精确解[11].最近，文献[12]中借助该方法构造了等谱4位势Ablowitz-Ladik(AL)方程的广义双Casoratian解.

本文利用[11]中的矩阵方法研究负向等谱4位势AL方程[13]

(1)

其谱问题为[13-14]

Φn+1=UnΦn，

其中

时间发展式为

Φn，t=VnΦn，

1 广义双Casoratian解

设E是一个位移算子，定义为Ekv(n)=v(n+k)，k∈Z.通常为了方便，在不引起混淆的情况下,记v(n)=vn.若在方程(1)中作分式变换

(2)

则fn，gn，hn，Fn，Gn，Hn满足双线性方程[15]

(3)

其中D是著名的Hirota双线性导数算子，定义为

设向量函数Φn和Ψn对一切n和t具有任意阶的导数，则Φn和Ψn的(m+p+2)阶双Casoratian行列式定义为[16]

Casm+1,p+1(Φn;Ψn)

=|Φn，EΦn,…,EmΦn;Ψn,EΨn,…，EpΨn|

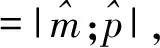
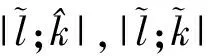
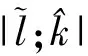
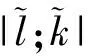
借助双Wronskian技巧，得到如下定理[17].

定理1负向等谱4位势AL方程(1)的双线性方程(3)具有双Casoratian行列式解

(4)

其中Φn,Ψn满足矩阵方程组

(5)

这里矩阵A=(aij)是与n，t无关的(m+p+2)×(m+p+2)阶任意的非奇异实矩阵.

于是，相应的负向等谱4位势AL方程(1)的解可表示为

(6)

2 孤子解和类有理解

方程组(5)存在通解

(7)

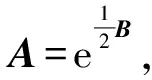
(8)

将(8)展开成级数得

(9)

若设矩阵B为对角线矩阵,

则有

由其构成的双Casoratian行列式fn，gn，hn，Fn，Gn，Hn是双线性方程(3)通常意义下的多孤子解[15]

若设矩阵

由于Bm+p+2=0，则(9)可截断为

从而Φn和Ψn的分量分别表示为

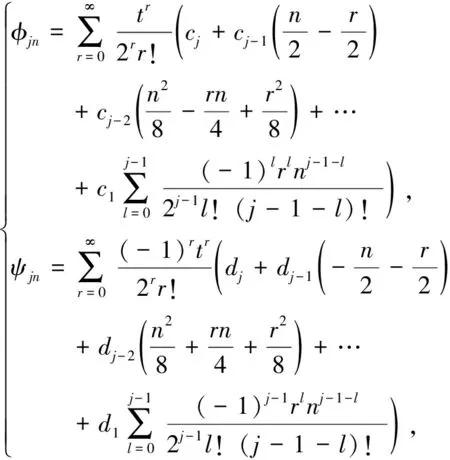
(10)

其中j=1,2,…,m+p+2.由其构成的双Casoratian行列式fn,gn,hn,Fn,Gn,Hn即为双线性方程(3)的类有理解.

特别地,若取c1=d1=1,ck=dk=0 (k=2,3,…,m+p+2)，则(10)化为

(11)

将(11)式代入(6)后即可得到方程(1)的双Casoratian行列式形式的类有理解.

如果取m=p=0,由(11)式可得

(12)

将(12)代入(4)，有

(13)

同理可得

(14)

于是,将(13)和(14)代入(2)式，得到方程(1)的类有理解为

另外，不难求出

(15)

将(12),(15)代入(4)，可类似解出方程(1)的前几个类有理解.

当m=1,p=0时，得到

当m=0，p=1时，解出

若取m=p=1，则有

(16)

将(16)代入(2)，可得此时方程(1)的类有理解.类似地，可分别算出在(m，p)=(2，0)和(m，p)=(0，2)条件下的类有理解.

参考文献:

[1] Freeman N C，Nimmo J J C.Soliton solutions of the KdV and KP equations:the Wronskian technique[J].Phys Lett A,1983，95(1):1.

[2] Nimmo J J C，Freeman N C.The use of Bäcklund transformations in obtainingNsoliton solutions in Wronskian form[J].J Phys A:Math Gen，1984，17(7):1415.

[3] Darboux G.Lecons surla théorie généerale des surfaces:Ⅱ[M].3rd ed.New York:Chelsea Publ Comp，1972.

[4] Liu Qiming.Double Wronskian solutions of the AKNS and the classical Boussinesq hierarchies[J].J Phys Soc Jpn，1990，59(10):3520.

[5] Hirota R，Ito M，Kato F.Two-dimensional Toda lattice equations[J].Prog Theor Phys Suppl，1988，94(94):42.

[6] Hirota R，Ohta Y，Satsuma J.Solutions of the KP equation and the two dimensional Toda equations[J].J Phys Soc Jpn，1988，57(6):1901.

[7] Ablowitz M J，Satsuma J.Solitons and rational solutions of non-linear evolution equations[J].J Math Phys，1978，19(10):2180.

[8] Nimmo J J C，Freeman N C.Rational solutions of the KdV equation in Wronskian form[J].Phys Lett A，1983，96(9):443.

[9] Zhang Dajun.Notes on solutions in Wronskian form to soliton equations:KdV-type[EB/OL].[2014-05-22].http://arxiv.org/abs/nlin/0603008.

[10] Wu Hua，Zhang Dajun.Mixed rational-soliton solutions of two differential-difference equations in Casorati determinant form[J].J Phys A:Gen Math，2003，36(17):4867.

[11] Chen Dengyuan，Zhang Dajun，Bi Jinbo.New double Wronskian solutions of the AKNS equation[J].Sci China Ser A，2008，51(1):55.

[12] Chen Shouting，Zhang Jianbing，Chen Dengyuan.Generalized double Casoratian solutions to the four-potential isospectral Ablowitz-Ladik equation[J].Commun Nonlinear Sci Numer Simulat，2013，18(11):2949.

[13] Zhang Dajun，Chen Shouting.Symmetries for the Ablowitz-Ladik hierarchy:I.Four-potential case[J].Stud Appl Math，2010，125(4):393.

[14] Ablowitz M J，Ladik J F.Nonlinear differential-difference equations[J].J Math Phys，1975，16(3):598.

[15] Chen Shouting，Zhu Xiaoming，Sun Xinxiu.N-soliton solution of a negative order isospectral four-potential Ablowitz-Ladik equation[J].江苏师范大学学报：自然科学版，2013，31(3):8.

[16] Gegenhasi，Hu Xinbiao，Levi D.On a discrete Davey-Stewartson system[J].Inverse Prob，2006，22(5):1677.

[17] Chen Shouting，Li Qi.Double Casoratian solutions of a negative order isospectral four-potential Ablowitz-Ladik equation[J].江苏师范大学学报：自然科学版，2013，31(4):11.