严寒地区村镇给水管道周围土壤温度场的数值模拟

白 莉 王 炎 刘晓龙

(1:吉林建筑大学市政与环境工程学院,长春 130118; 2:吉林建筑大学土木工程学院,长春 130118)

土壤与大气时刻进行着热量和水分交换,气候因素的改变会引起土壤中水热状况的变化，以及土壤中物理和化学变化.随着气候因素的改变，土壤的温度场也会随之发生变化,这将直接影响埋地管道运行的安全可靠性;同时,埋地管道与周围土壤发生的热湿交换也在时刻影响着土壤温度场.因此，开展土壤温度场的研究,对于研究土壤源热泵地下换热器性能和浅埋管道运行安全可靠性具有重要意义.

Matlab是一个将数值分析、矩阵计算、科学数据可视化，以及非线性动态系统的建模和仿真等诸多强大功能集成一体的大型软件,近年来,借助于Matlab软件仿真模拟埋管周围土壤温度场的研究越来越广泛.本文将利用利用Matlab-PDE工具箱模拟采取防冻胀措施的给水管道周围土壤温度场.

1 物理模型

在《建筑给水排水设计规范》(GB 50015-2003,2009年版)中的3.5.3条文明确规定:室外给水管道的覆土深度,应根据土壤冰冻深度、车辆荷载、管道材质及管道交叉等因素确定,管顶最小覆土深度不得小于土壤冰冻线以下0.15m,行车道下的管线覆土深度不宜小于0.70m.在我国严寒地区城市基本都将给水管道敷设在当地冰冻线以下,但在广大农村,由于地下水位和施工技术等经济技术条件的限制,难以保障给水管道埋深在当地冰冻线以下,给水管道时常发生冻胀现象.

为了解决严寒地区村镇给水管道的冻胀问题,克服村镇给水管道深埋工程施工土方量大,施工工期长等弊端,课题组在大庆地区林县实验基地采用了一种具有良好防水性能和保温性能的新型给水管道——外管采用聚丙烯管材(PPR),内管采用聚氯乙烯管材(PVC)的给水管材,其中间层采用发泡的聚氨酯硬质泡沫作为保温层的双层管道.经过计算管道推荐浅埋深度为1.3m时,保温层厚度为50mm[1],建立浅埋保温给水管道与周围土壤非稳态传热，以及土壤自身导热物理模型如图1所示,计算区域网格划分如图2所示.

1.1 边界条件

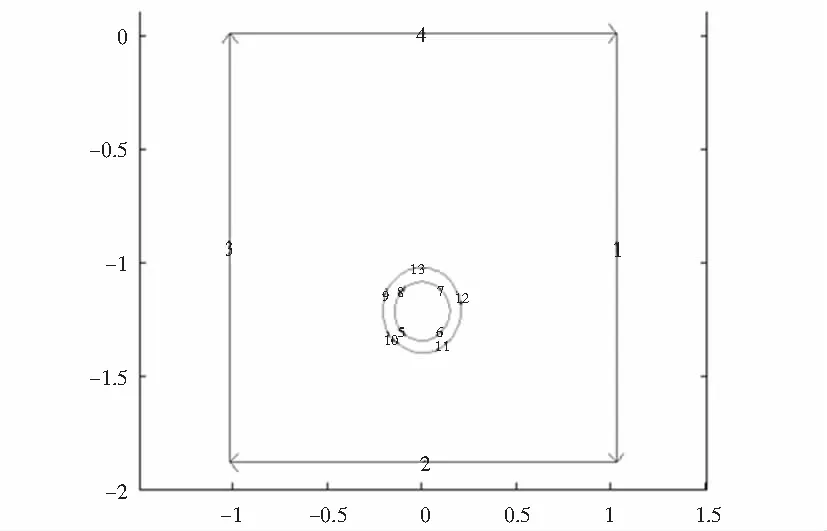
图1 浅埋给水管道周围土壤物理模型

边界1属于第二类边界条件:q1=0

(1)

边界2属于第一类边界条件:t2=t0

(2)

其中:t0为地表土壤年平均温度,℃.

边界3属于第二类边界条件:q3=0

边界4属于第三类边界条件:

(3)

te=t0+Acos(ωτ+φ)

(4)

其中,λ4为土壤导热系数,W/m.℃;h4为土壤表面与空气的换热系数,W/m2.℃;t0为地表空气年平均温度,℃;te为不同深度的土壤温度,℃;A为地表空气年温度波幅,℃;ω为以年为周期的角速度,rad/y;τ为累计时间,y;φ为初相角,rad.

边界9-13,属于第三类边界条件:

图2 计算区域网格

(5)

其中,λ9-13为管道保温层的导热系数,W/m.℃;αi为内表面换热系数,W/m2.℃;te为周围土壤温度,℃;T5-8为管道保温层内壁的温度,℃.

由于给水管道内管壁厚度相对于温度影响区域而言非常小,因此忽略给水管道内管(聚丙烯管材)管壁的传热情况,并且近似的认为保温层内壁的温度即为管道内流体的温度:

T5-8=Tf

(6)

其中,Tf为管道内流体的温度,℃.

同理,由于给水管道外壁厚度相对于温度影响区域而言非常小,因此忽略给水管道外管(聚氯乙烯管材)管壁的传热,认为保温层外壁的温度即为土壤温度:

T9-13=Te

(7)

1.2 控制方程

为了便于理论分析,方便软件对物理模型的求解,做出以下假设:认为管内水流速度均匀,压力恒定,忽略土壤沿管道轴向的热损失,忽略土壤的水分迁移引起的热湿变化.

(8)

其中,Te为土壤温度,℃;为累计时间;α为土壤的热扩散率,m2·S-1.

2 基于Matlab-PDE 求解物理模型

2.1 Matlab-PDE Tool 求解思路

基于有限元的Matlab-PDE 工具箱，在研究和求解二维空间的偏微分方程上具有高效性、准确性和直观性.本文利用Matlab软件的PDE工具箱对该浅埋保温给水管道与周围土壤非稳态传热，以及土壤自身导热物理模型进行求解.本文中的物理模型计算过程中采用抛物线热传导方程:

(9)

其中,ρ为密度,kg/m3;C为比热,J/(kg·K);λ为导热系数,w/(m·℃).

初始条件:

T(0)=T0(0)

(10)

边界条件计算中应用了Neumannn条件:

(cT)+qT=g

(11)

边界条件计算中应用了Dirichlet条件:

hT=r

(12)

将抛物线方程简化成椭圆型方程来求解,通过PDE toolbox函数parabolic完成的[2].

得到系数与时间无关的椭圆型方程:

-·(cT)=0

(13)

对整个求解空间Ω作三角形网格剖分,对于任意给定t≥0,PDE的解按有限元法的基底可以展开成:

(14)

将展开式代入方程(11),两边乘以试验函数φi,然后在Ω上积分,利用Green公式和边界条件,可得：

(15)

上式可以写成大型的线性稀疏的常微分方程组:

(16)

式(10)的初值为:

Ti(0)=T0(0)

(17)

得到每一个节点xi,任一时刻t的ODE解.这里K和F为原边界条件下椭圆型方程-·(cT)=0在Ω的刚度矩阵和荷载向量.M是质量矩阵.得到了K和F,在Matlab环境下即可解出节点温度的近似解T及热流.

2.2 Matlab-PDE Tool 求解结果

将DN50mm的给水管道外加传热系数为0.033W/(m.℃)的聚氨酯硬质泡沫保温层,保温层厚度为50mm,保温层的密度为45kg/m3,比热容约为2 380.0J/(kg.℃)将管道埋至-1.3m,认为地表土壤温度-23℃,埋深为-1.8m处温度为-3.3℃,给水管道内流体温度为12℃,土壤导热系数取1.33W/(m.℃),土壤密度为2 050kg/m3,土壤比热容取值1 840J/(kg.℃),应用Matlab—PDE Tool求解出,采用该抗冻胀技术的给水管道与周围土壤非稳态传热，以及土壤自身导热物理模型，在冬季连续运行半个月,一个月,两个月和三个月后管道周围土壤温度场如图3～6所示.

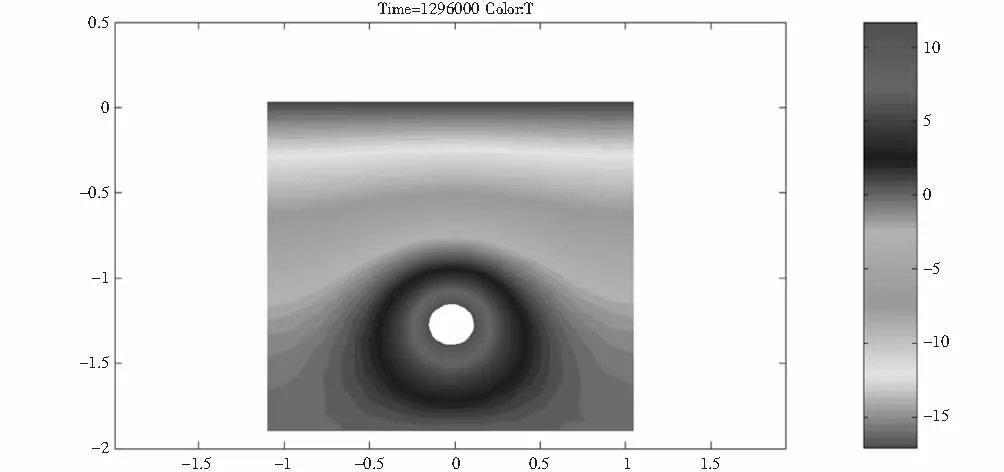
图3 管道运行半个月周围土壤温度场

图4 管道运行一个月周围土壤温度场

图5 管道运行两个月周围土壤温度场

图6 管道运行三个月周围土壤温度场

3 结语

(1) 从图3～图6对比发现,埋地管道周围同一地点的土壤温度随着模拟时间增加而降低;这是因为土壤在和大气不停进行热湿交换致使土壤温度越来越低；

(2) 保温管道周围的温度梯度随着时间的变化而变化,基本的趋势是管道上方的温度梯度大于管道下方的温度梯度,其原因是上方土壤温度较低、温差大,因而换热量也较大；

(3) 随着模拟运行时间增加,保温给水管道内部存在热流影响的范围在逐步扩大,这主要是因为随着时间变化管道内部流体与周围土壤换热,使周围温度较低的土壤温度有所升高,温度升高的土壤又再影响周围的土壤温度场；

(4) 当模拟管道运行三个月后,发现在给水管道内部流体温度为12℃,外部大气-23℃的地区(如大庆地区)采用50mm的硬质聚氨酯泡沫保温层的PPR-PVC给水管道,敷设在-1.3m,管道保温层外壁基本能保持在2℃～5℃,就是说明采用50mm的硬质聚氨酯泡沫保温层,即该浅埋外加保温层的给水管道防冻胀技术可以保证管道不发生冻胀现象；

(5) 基于有限元方法的Matlab-PDE 工具箱可以解决复杂边界条件的非稳态问题,其求解图形可视化功能使得计算结果更加直观,便于对比分析.

参 考 文 献

[1] 王 炎,白 莉,化亚魏.冻土地区村镇给水管道保温层厚度数值计算[J].吉林建筑大学学报,2014,31(1):41-44.

[2] 苏金明,阮沈勇.MATLAB7.0实用指南(下册)[M].北京:电子工业出版社,2004:167-168.