交通流影响因子与道路交通噪声的关系研究

冯 霞，孙凤英，胡 薇

(东北林业大学 交通学院，哈尔滨 150040)

近年来，随着城市交通的快速发展，机动车数量的迅猛增长，道路交通噪声污染越来越严重。而道路交通噪声会对人类产生很大危害，包括对人耳听力的损伤、对睡眠的干扰、对人体的生理影响和心理影响[1]。因此急需控制交通噪声污染。国内外大量研究表明，交通噪声与交通流影响因子(车流量、速度、车型比、路面宽度等)存在着很大关系[2～5]。因此，本文将研究交通流影响因子与道路交通噪声之间的关系，为未来交通噪声的预测提供一定的思路，这对控制噪声污染有着一定的重要意义。

1 交通流影响因子与道路交通噪声的关系建模

美国FHWA道路交通噪声预测模型，经多次改进，比较完善、预测精度高，在许多国家得到广泛应用[6]，但模型建立时依据的环境标准、道路状况和车辆分类等与我国的实际情况存在着一定的差异，应用在我国道路交通噪声预测中并不能保证预测的精度。因此，本文将对美国FHWA道路交通噪声预测模型进行修正，建立适合我国的交通流影响因子与道路交通噪声的关系模型。

美国FHWA道路交通噪声预测模型的建模思想是，将道路上行驶的车辆分为三类，先求出各类车流的小时等效声级Leqi，再将三种类型车流的等效声级进行叠加，得到总车流等效声级Leq。而某类车流的小时等效声级是在对此类基本车流参考噪声级的基础上进行流量、车速、有限长路段、地面及遮挡物等影响因素修正后得到的[7-8]。Leqi和Leq的计算公式分别见公式(1)和公式(2)。

(1)

(2)

式中：Leqi为第i类车型交通流的小时等效声级，dB(A)；L0i为第i类车型交通流的参考声级，dB(A)；Qi为在时间段T内经过测量点的第i类车型车流量；r0为参考距离，r0=15 m；r为预测点到车道中心线的垂直距离，m；Vi为第i类车型车辆的平均车速，km/h；T是测量时间，T=1 h；β为地面覆盖系数，β=0或0.5；Δφ是有限长路段的修正量，dB(A)；ΔS是遮挡物衰减量，dB(A)；n为车型种类数。

Δφ，ΔS，β分别是有限长路段、遮挡物、地面覆盖系数对某车型交通流等效声级的修正，他们对噪声的影响只依赖于环境条件，因此可将他们对噪声的影响从公式(1)中分离出来，看做是L环境，其计算公式见公式(3)；公式(1)中分离后剩下的项所组成的部分即为第i类车型交通流噪声的理想模型，用L1i来表示，其计算公式见公式(4)。

(3)

(4)

由上述FHWA的预测模型建模思想可知，确定各车型交通流的参考声级是非常重要的。美国各车型交通流的参考声级计算公式应用在我国不一定适合，而且实际道路上车辆是以混合交通流的形式运行的，交通噪声监测时若将混合车流分离成不同车型的车流，分别确定各车型交通流的参考声级较困难。因此，本文引进等效流量与等效车速的概念，将道路上运行的总交通流等效为某个车型的交通流。这样，即可将车流量、车速、车型比及路面宽度4个交通流影响因子对道路交通噪声的影响转化为等效车流量、等效车速及路面宽度3个因子对道路交通噪声的影响，从而建立交通流影响因子与道路交通噪声关系的理想模型。

车辆分类方法及车流量的折合系数，参照《高速公路交通噪声监测技术规定(暂行)》，见表1。

表1 车型分类和车流量折算系数

根据噪声的能量叠加原理，等效车流量Q为道路中各类型车辆的流量经折算后的相加值，计算公式见公式(5)。等效车速V的计算式，见公式(6)。

Q=8QL+3.5QM+QS。

(5)

(6)

公式(5)和公式(6)中，QL，QM，QS分别为大、中、小型车流量，VL，VM，VS分别为大、中、小型车平均车速。

通过分析公式(4)，可以看出L1i与第i类车参考声级L0i成线性关系，与流量Qi、平均车速Vi和预测点的相对距离r0/r成对数线性关系。而FHWA道路交通噪声模型中L0i跟平均车速Vi也成对数线性关系。引入等效流量及等效车速的概念后，可以认为L1跟L1i一样，与等效车流量Q、等效车速V及预测点的相对距离r0/r成对数线性关系。因此，可建立交通流影响因子与道路交通噪声关系的对数线性模型，见公式(7)。

(7)

2 模型参数的确定

由于所建立的交通流影响因子与道路交通噪声关系的模型是线性模型，因此本文运用统计软件SPSS 13.0，采用线性回归分析方法确定模型中参数Ai的大小。

2.1 采集建模数据

选取哈尔滨市18条道路的50个测点进行数据采集，包括各类型车的流量、车速及测量距离等。具体测量方法如下：

把录像机固定在三脚架上，调整三脚架的高度及角度，并对准道路上运行的车辆，以获取各类型车流量；一人将雷达测速仪对准车辆，测试车辆的运行速度，另外一人负责记录各类型车辆的速度；在人行道上，距离道路边沿20 cm处，放置另外一个三脚架，将积分声级计固定在三脚架上，调整三脚架高度为1.2 m，测量等效连续声级；记录道路的车道数及宽度。

2.2 数据整理

观看录像，统计各车型的交通量，并计算各车型车辆的平均车速。用Excel计算等效车流量Q，等效车速V及r0/r对数值的大小。

2.3 SPSS数据处理

随机选取采集样本中42个测点的测量数据，将等效车流量的对数值lgQ，等效车速的对数值lgV，r0/r的对数值lg(r0/r)作为自变量，等效声级Leq作为因变量，应用SPSS软件进行回归分析。

2.4 SPSS结果分析

经SPSS统计分析后，得出各参数的大小分别为：

A1=9.448，A2=3.374，A3=0.789，A4=36.322。

因此，哈尔滨市交通流影响因子与道路交通噪声关系的模型为：

该模型经过F检验，p概率值为0，小于0.05，表明建立的回归模型显著性较高，即lgQ，lgV及lgr0/r整体上对Leq有高度显著的线性影响。调整后的判定系数大小为0.75，说明模型的拟合度较高。

3 模型验证

运用上述建立的道路交通噪声模型对剩余8个测点的噪声进行预测，并将预测值与实测值进行对比分析。实际监测值与预测值的大小见表2，通过表2可以看出预测值与实际值的最大差值为1.4 db，表明模型拟合效果很好。

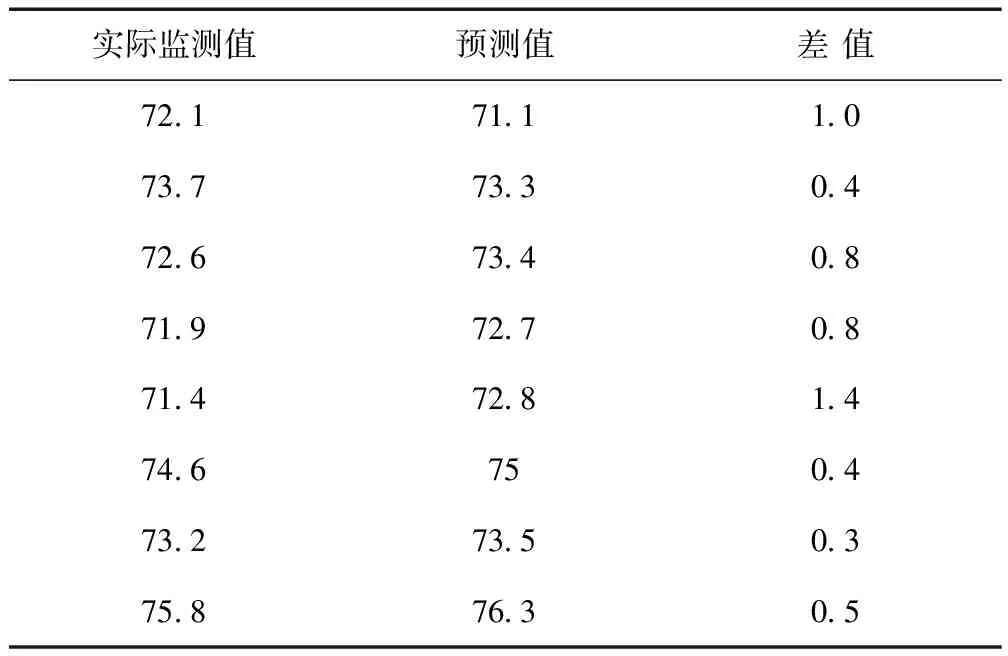
表2 道路交通噪声预测值与实测值的对比 db

4 结 论

(1)通过对美国FHWA道路交通噪声预测模型的修正，建立的交通流影响因子与道路交通噪声的关系模型，更适用于我国道路交通噪声的预测。

(2)该模型经过验证，预测值与实际监测值相差不大，误差在0.3～1.4dB，可用于道路交通噪声的预测。

【参 考 文 献】

[1]李 江.交通工程学[M].北京：人民交通出版社，2002.

[2]李 丹.青岛市快速路交通噪声影响与防治对策研究[D].青岛：青岛理工大学，2008.

[3]徐洪波.道路宽度及车速对交通噪声的影响[J].环境保护科学，2007，33(6)：127-128.

[4]徐 涵.城市道路改造对道路交通噪声的影响分析与对策研究[D].哈尔滨：哈尔滨工业大学，2011.

[5]刘 涛.城市道路交通噪声影响因素与传播规律分析[D].西安：长安大学，2009.

[6]范东平.道路交通噪声预测模型分析及实证研究[D].广州：广东工业大学，2012.

[7]刘华炜.哈尔滨市道路交通噪声污染分析及防护研究[J].森林工程，2013，29(3)：105-107.

[8]王 弘.高速公路交通噪声预测模式在典型路段的应用效果及修正[D].广州：暨南大学，2006.