基因表达数据在邻域关系中的特征选择
陈玉明,吴克寿,李向军
(1. 厦门理工学院 计算机科学与技术系,福建 厦门 361024; 2. 南昌大学 计算机科学与技术系,江西 南昌 330031)
美国人类基因组计划(HGP)把基因组信息学定义为:它是一个学科领域,包含着基因组信息的获取、处理、存储、分配、分析和解释的所有方面。基因表达数据分析的对象是在不同条件下,全部或部分基因的表达数据所构成的数据矩阵。通过对该数据矩阵的分析,可以回答一些生物学问题。随着试验技术及仪器的不断改进和基因组数据的急剧增长,现代DNA微阵列或芯片技术产生的各种基因表达数据均规模庞大、内容复杂。如何有效地分析利用这些数据成为生物信息学中的挑战性课题。在基因表达数据分析中,基因的数目成千上万,但往往只是很少一部分的关键基因影响样本的分类,其他的基因往往是冗余的或者是不重要的。在设计基因表达数据分类器之前进行特征选择,可以有效降低分类器的时间复杂度,提高分类精度。目前最常用的基因表达数据特征选择方法主要有2类:基于过滤算法(filter)的选择方法[1]与基于wrapper的选择方法[2]。基于filter的基因表达数据特征选择方法使用数据本身的内在特性作为评价基因的准则,但通过filter选择出来的若干个基因可能具有较强的相关性。基于wrapper的基因表达数据特征选择方法根据分类器的某种性能来评价基因或基因子集的重要性,而基于wrapper方法在基因的选择过程中反复调用分类算法,往往造成较高的时间复杂度。
粗糙集由波兰科学家Pawlak于1982年提出[3],用于处理不确定、不一致、不精确数据的数学理论工具。现已广泛应用在人工智能、数据挖掘、机器学习等领域[4-7]。然而,Pawlak粗糙集只能处理离散化的数据,对于现实世界广泛而大量存在的连续数据却缺乏有效的处理能力。基因表达数据也往往都是连续的,目前大多数方法是将基因表达数据先进行离散化[8],离散化过程必定会造成某种程度的信息丢失,并影响分类系统的分类精度。
1 邻域关系
传统粗糙集理论采用等价类形式化地表示知识分类。然而,等价类是基于离散型的数据形成的等价关系划分而得到的,对于连续型的数据并不能构造合适的等价类。因此,下面引入邻域关系处理连续型的基因表达数据,用于基因表达数据的特征选择。

定义2 给定邻域信息系统IS=(U,A,V,f,δ),对于任一x,y∈U,B⊆A,B={a1,a2,...,an},定义B上的距离函数DB(x,y)满足:
1)DB(x,y)≥0,非负;
2)DB(x,y)=0,当且仅当x=y;
3)DB(x,y)=DB(y,x),对称;
4)DB(x,y)+DB(y,z)≥DB(x,z)。
式中:
DB(x,y)=
当p=1时,称为曼哈顿距离,当p=2时,称为欧氏距离。


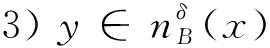

2 基于邻域关系的基因选择方法
基于等价关系的信息熵、互信息、粗糙熵等概念度量了知识的粗细程度,也反映了决策系统中的分类能力大小,但主要处理离散型数据的决策系统,对于连续型的数据并不能够直接处理。下面结合邻域关系与邻域类的定义,进一步定义了邻域特征选择概念,用于连续型的基因表达数据的特征选择当中。同时,提出一种基于邻域关系的启发式基因表达数据特征选择算法。
2.1 邻域特征选择
定义5 定义DT=(U,C∪D,V,f,δ)为一个邻域决策表,其中C为条件特征,特征值为连续型的数据,邻域阈值为δ,其邻域划分为U/NRδ(C)={X1,X2,...,Xm},D为决策特征,决策特征是一些决策分类信息,为离散型的数据,以等价关系划分为U/D={Y1,Y2,...,Yn}。
定义6 设DT=(U,C∪D,V,f,δ)为一个邻域决策表,∀B⊆C,X⊆U,记U/NRδ(B)={B1,B2,...,Bi},则称B*(X)δ=∪{Bi|Bi∈U/NRδ(B),Bi⊆X}为X关于B的邻域下近似集,称B*(X)δ=∪{Bi|Bi∈U/NRδ(B),Bi∩X≠∅}为X关于B的邻域上近似集。
定义7 设邻域决策表DT=(U,C∪D,V,f,δ),其中C为条件特征,特征值为连续型的数据,邻域阈值为δ,D为决策特征,决策特征是一些决策分类信息,为离散型的数据。定义决策特征D对条件特征C的邻域依赖度为γC(D)δ=|C*(D)δ|/|U|,其中|U|表示集合U的基数。
定义8 设邻域决策表DT=(U,C∪D,V,f,δ),对∀b∈B⊆C,若γB(D)δ=γB-{b}(D)δ,则称b为B中相对于D是不必要的;否则称b为B中相对于D是必要的。对∀B⊆C,若B中任一元素相对于D都是必要的,则称B相对于D独立。
定义9 设邻域决策表DT=(U,C∪D,V,f,δ),若∀B⊆C,γB(D)δ=γC(D)δ且B相对于D是独立的,则称B是选取的关键特征组,这一特征选取过程称为邻域特征选择。
性质1 设邻域决策表DT=(U,C∪D,V,f,δ),若B1⊆B2⊆...⊆C,则0≤γB1(D)δ≤γB2(D)δ≤...≤γC(D)δ≤1。
定义10 设邻域决策表DT=(U,C∪D,V,f,δ),∀a∈C,R⊆C,定义a相对于R的特征重要度为Sign(a,R,D)=γR∪{a}(D)δ-γR(D)δ。
2.2 基于邻域关系的基因选择算法
性质1表明邻域依赖度具有单调性,因此可以采用删除法或添加法进行特征选择,基因表达数据可以表示成前面定义的邻域决策表,依据上述邻域特征选择的定义,可设计如下基于邻域关系的基因选择算法。下面以定义10的特征重要度为启发式信息设计了一种基于邻域关系的基因选择算法。
算法GSNRS(基于邻域关系的基因选择算法)
输入:基因表达数据决策表DT=(U,C∪D,V,f,δ);
输出:DT的一个邻域约简R。
1)计算整个条件特征集C相对于决策特征D的邻域依赖度为γC(D)δ。
2)R:=C。
3) 当γR(D)δ=γC(D)δ重复:
①对所有的a∈R计算特征重要度Sign(a,R,D);
②在R中选择特征a满足特征重要度最小;
③R:=R-{a}。
4) 输出R。
在算法中,每次选择特征重要度最小的特征,若去掉它后决策表的邻域依赖度仍然不变,则可以去掉,否则保留下来,依次进行下去,直到得到一个条件特征子集,在其中去掉任何一个特征,决策表的邻域依赖度都会改变,则算法结束,该特征子集即为所选取关键特征组。
3 实验结果与分析
下面选用2个标准的基因表达数据集来验证GSNRS算法的有效性。2个标准基因表达数据集分别为Lymphoma和Liver cancer。Lymphoma数据集包含了96个样本,4 026个特征基因,其中54个Othertype子类和42个B-celllymphoma子类。Liver cancer数据集包含了156个样本,1 648个基因,其中82个HCCs子类和74个nontumorlivers子类。实验基因数据集如表1所示。

表1 基因表达数据集
在Lymphoma和Livercancer基因表达数据中分别采用文献[9]中粗糙集的特征选择算法TRS与本文邻域特征选择算法GSNRS进行比较。首先进行预处理,对于有缺失值的数据采用文献[10]的方法进行完备化。基因表达数据集是连续型的数据,对于经典粗糙集特征选择算法,需要对其数据进行离散化,离散化过程采用文献[8]中的方法进行。而本文GSNRS特征选择算法,不需要离散化。设邻域参数为δ=0.1,特征选择结果如表2所示。

表2 基因数据集特征选择结果
由表2可知,TRS算法在Lymphoma数据集中选择出7个关键基因,在Liver cancer数据集中选择出6个关键基因。GSNRS算法在Lymphoma数据集中选择出6个关键基因,在Liver cancer数据集中选择出5个关键基因。下面再比较2组基因的分类能力,分别针对选取的关键基因采用KNN,C5.0分类器进行分类实验,并用留一交叉法检验分类精确率,实验结果如表3所示。

表3 基因分类精确率
上述实验结果表明,基于粗糙集的基因选择方法和基于邻域关系的基因选择方法都能正确提取有效的基因。基于邻域关系的基因选择方法不需要离散化,而且由于避免了离散化过程的造成的信息丢失,提取的特征基因个数较少。在分类精度上,基于邻域关系的基因选择方法提取的基因优于基于粗糙集的基因选择方法提取的基因。
4 结束语
传统粗糙集理论中的特征选择方法往往难以处理连续性的基因表达数据,成为基因表达数据研究中的主要缺陷和障碍。本文针对传统粗糙集理论中难以处理连续数据的缺点,在特征选择中引入邻域关系,定义了邻域依赖度与邻域特征选择等概念,提出了一种基于邻域关系的基因特征选择方法。该特征方法不用对数据进行离散化,避免了信息损失,从而提高了被选择基因的分类准确率。拓展了粗糙集理论的应用范围,为基因表达数据分析技术提供了一种新的尝试。
参考文献:
[1]TIBSHIRANI R, HASTIE T, NARASHIMAN B, et al. Diagnosis of multiple cancer types by shrunken centroids of gene expression[C]//Nat’1 Academy of Sciences. [S.l.], USA, 2002: 6567-6572.
[2]KOHAVI R, JOHN G H. Wrappers for feature subset selection[J]. Artificial Intelligence, 1997, 97(1/2): 273-324.
[3]PAWLAK Z. Rough sets[J]. International Journal of Computer and Information Science, 1982, 11(5): 341-356.
[4]BANERJEE M, MITRA S, BANKA H. Evolutinary-rough feature selection in gene expression data[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C: Application and Reviews, 2007, 37: 622-632.
[5]YANG Ming, YANG Ping. A novel condensing tree structure for rough set feature selection[J]. Neurocomputing, 2008, 71(4/5/6): 1092-1100.
[6]QIAN Yuhua, LIANG Jiye. Positive approximation: an accelerator for attribute reduction in rough set theory[J]. Artificial Intelligence, 2010, 174(9/10): 597-618.
[7]CHEN Yuming, MIAO Duoqian. A rough set approach to feature selection based on power set tree[J]. Knowledge-Based Systems, 2011, 24(2): 275-281.
[8]苗夺谦. Rough set理论中连续属性的离散化方法[J]. 自动化学报, 2001, 27(3): 296-302.
MIAO Duoqian. A new method of discretization of continuous attributes in rough sets [J]. Acta Automatica Sinica, 2001, 27(3): 296-302.
[9]王国胤. Rough 集理论与知识获取[M]. 西安: 西安交通大学出版社, 2001:24-28.
[10]GRZYMALA-BUSSE J W. Handling missing attribute values[M]. [S.l.]: Springer, 2005: 37-57.

