多功率锚节点辅助的DV-Hop定位算法

陶志勇，魏强，刘影

辽宁工程技术大学电子与信息工程学院，辽宁葫芦岛 125105

多功率锚节点辅助的DV-Hop定位算法

陶志勇，魏强，刘影

辽宁工程技术大学电子与信息工程学院，辽宁葫芦岛 125105

在无线传感器网络中，DV-Hop定位算法在计算未知节点到锚节点的距离以及通信半径之内相邻节点跳距时存在较大误差，提出了一种锚节点辅助的分布式定位算法。此算法不需要任何测距技术支持。它是利用锚节点的功率控制，即以不同的发射功率发射信标信号，接收到信标信号的未知节点将这些信标信息记录。此外还考虑了用全网锚节点来修正单独锚节点的平均每跳距离，用极大似然法计算节点坐标。Matlab仿真实验结果表明，在相同网络环境下，该算法能有效减小距离计算带来的定位误差，可适合实际定位情况且具有较高的定位精度。

无线传感器网络；节点定位；锚节点；平均每跳距离；极大似然法；距离向量算法

1 概述

无线传感器网络（Wireless Sensor Network，WSN），是由大量智能传感器节点构成，通过无线通信方式构成的一个多跳的网络系统，具有环境适应性、自组织和低成本的特点。在很多领域已经实施应用，例如目标跟踪、环境监测、战场侦察、生物医疗、抢险救灾以及工业监控等领域，WSN具有广阔的应用前景[1-2]。

无线传感器网络定位分为自定位和对外定位两种，其中无线传感器网络中定位技术是最关键的技术之一。无线传感器网络自定位是通过少数已知位置的节点来确定大多数未知节点的位置。传感器网络的定位算法一般有以下特点：自组织性、节点数量庞大、动态性、容错性好、高可靠性、能采用分布式计算的机制、遵守能量高效利用的原则。

根据定位机制，可将现有的无线传感器网络自定位算法分两类：一是基于测距技术的定位算法Range-Based，例如RSSI（Received Signal Strength Indicator）[3]、TOA（Time of Arrival）、TDOA（Time Difference on Arrival）、AOA（Angel of Arrival）；二是基于无需测距的定位算法Range-Free，如DV-Hop（Distance Vector-Hop）算法[4]、凸规划算法、MDS-MAP算法、质心算法等。

基于测距的定位机制由于实际测量节点间的距离或角度或时间，因此节点需要安装特殊的硬件设备。通常定位精度相对比较高，但对节点的硬件要求也较高，实现起来较复杂，定位过程中消耗的能量也比较多，而且这些测量信息极易受衰弱、干扰等影响。无需测距定位算法不需要测量节点间的距离或角度，对硬件要求也简单，实现也方便，适用于部分不需要高精度的场合。因为功耗和成本的因素，所以基于无需测距定位算法受到了广泛关注。

DV-Hop算法是目前研究和应用最为广泛的基于无需测距的定位算法，并且对硬件要求较低，实现简单。但在计算未知节点和锚节点间的距离时估算较粗糙、误差较大。当节点间跳数为1跳时，不管两节点之间距离到底多远或多近，DV-Hop定位算法计算出的距离是一样的，这就会对定位造成误差。当节点跳数大于1跳时，大部分节点之间是成折线的不是直线的，算法是用折线距离代替节点之间的实际距离因此也会带来误差。如果跳数越多，未知节点与锚节点之间路径偏离两点直线连线的可能性越大，计算出的未知节点与锚节点估计距离与真实距离误差越大。现阶段，对DV-Hop算法的改进方法主要有：（1）与其他的定位算法相结合[5]；（2）修正未知节点与锚节点间的距离[6]；（3）改进最后一步的定位计算方法[7]，而对DV-Hop算法本身的参数优化研究较少，定位精度不是很高，适用于定位精度要求比较低的环境中。本文对参数进行了详细的分析并且提出了一种新的利用锚节点功率控制计算节点间距离，结果表明可以有效地提高DV-Hop算法的定位精度。

2 DV-Hop定位算法过程

DV-Hop算法的基本思想[8-11]：用网络中节点之间的平均每跳距离和节点间的跳数乘积表示待定位节点间距离，然后采用三边定位法获取节点的位置信息。

DV-Hop算法步骤[12-14]：

第1步：计算最小跳数。

第2步：计算各节点间的实际跳数距离。第i个锚节点的平均每跳距离为：

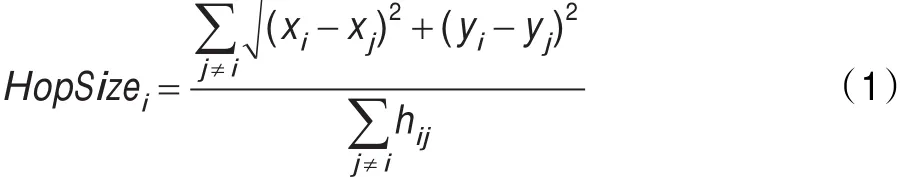
式中(xi，yi)、(xj，yj)为锚节点i、j坐标，hij为锚节点i、j之间的最小跳数。

第3步：定位未知节点位置。将估算的平均每跳距离作为一个校正值广播至网络中，待定位的节点接收到校正值后，根据跳数信息计算与参考节点间的距离。利用三边测量法或极大似然估计法计算出未知节点的位置。

3 多功率锚节点辅助的DV-Hop定位算法

3.1 多功率锚节点分布模型

当未知节点与锚节点间的跳数为1跳时，计算出的估计距离是一个定值。例如，节点随机分布在网络环境中，节点的通信半径R为30 m，根据DV-Hop算法计算得到的平均每跳距离为21 m，假设1跳之内有两个未知节点a、b，它们到锚节点的实际距离为3 m、15 m。根据算法得出未知节点到锚节点的估计距离均为21 m，则用估计距离21 m代替实际距离3 m和15 m会有很大的误差。如果能获得未知节点到锚节点相对更准确的距离无疑能提高未知节点的定位精度，因此本文依据与锚节点进行通信时，控制锚节点的发射功率来调节信号传输最大半径，假如，锚节点有N个级别的发射功率，其对应的信号传输最大半径分别为Ri，i=1，2，…，N。这样就可以控制锚节点传输不同长度的半径。本文采用锚节点有3级发射功率，如图1所示，对应半径就有三种R1、R2、R3，在这里R1取R/3，R2为2R1，R3为R。特殊说明，锚节点有三个通信半径，未知节点只有一个通信半径R。

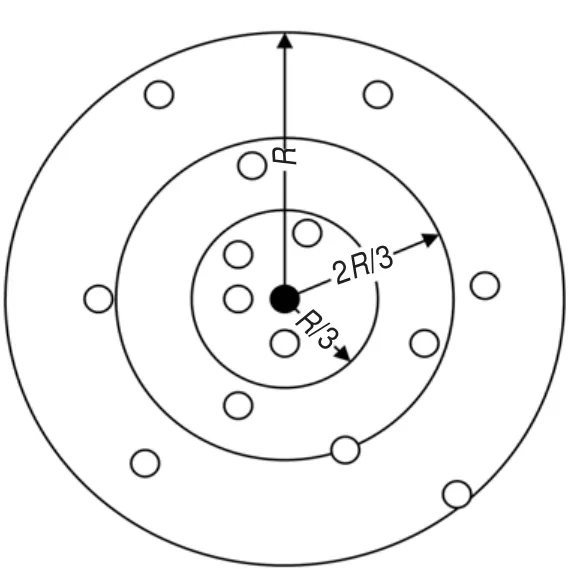
图1 锚节点3级发射功率节点分布示意图

锚节点以通信半径R（即R3）向网络中广播位置信息数据包，以得到所有节点到各个锚节点的最小跳数并记录。其次，锚节点分别再以R1、R2通信半径向全网广播，并统计在通信半径R1范围内的未知节点和在通信半径R1、R2之间的未知节点。这样未知节点到锚节点的距离分为四种情况。第一种情况是统计R1范围内未知节点到锚节点的距离为1/3×HopSizei；第二种情况是未知节点在R1～R2范围内，计算估计距离为2/3×HopSizei；第三种情况是未知节点在R2～R范围内，计算到锚节点的距离是HopSizei；第四种情况就是当跳数大于1跳时，计算估计距离为di。四种情况具体如下式(R=3R1=1.5R2)：

这样在上面的例子中，未知节点a在R1=10范围之内，所以就用7 m取代原来的21 m，节点b在通信半径R1～R2所以就用14 m取代原来的21 m，虽然与实际距离还有误差，但总比原来的21 m来估计距离无疑提高了不少。使离未知节点1跳的锚节点的估计距离更接近实际距离，这样就能达到提高定位精度的目的。

3.2 距离校正值修正

在经典的DV-Hop算法中计算每个锚节点的平均每跳距离时，如果算出的平均每跳距离误差大会造成DV-Hop算法一系列误差，最终定位肯定不准确。算法中计算平均每跳距离是等于锚节点间距离之和除以锚节点间跳数之和。但是求未知节点到各个锚节点的距离只需最先到达的锚节点平均每跳距离，而未考虑其他节点的影响。本文改进的算法在计算锚节点的平均每跳距离时不仅考虑最先接收到的平均每跳距离，同时也要考虑网络环境中其他锚节点的平均每跳距离。

根据经典DV-Hop算法求出各个锚节点的平均每跳距离，综合考虑所有节点对定位精度的影响。把所有锚节点的平均每跳距离求均值定义为全网平均每跳距离。

Hdave为全网平均每跳距离；Hdi为第i个锚节点的平均每跳距离；n为锚节点的个数。

在此基础上，对Hdave和Hdi求均值得到修正后的锚节点平均每跳距离Hi，这样就充分地把所有锚节点分布考虑在内，进而达到减小误差的效果。

利用反馈的思路来验证求得的平均每跳距离是否误差较大，从而更进一步改进平均每跳距离。用已经求得的平均每跳距离计算各个锚节点之间的距离——平均每跳距离乘以跳数即得锚节点之间的距离。锚节点是位置已知的节点，各个锚节点之间的真实距离可以得知，比较用平均每跳距离乘以跳数求得的估计距离和真实实际距离两者之间的差距，并计算误差。计算平均每跳距离误差为：

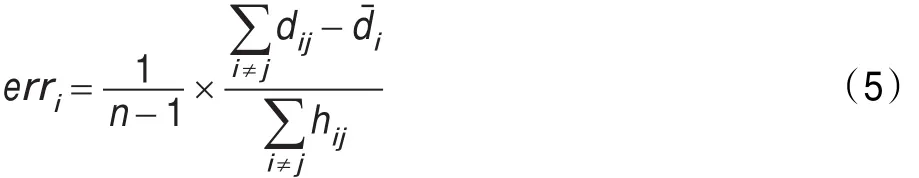
dij为锚节点i，j之间的真实距离，dˉi是锚节点i到锚节点j之间的估计距离，hij为两锚节点间的跳数，n则为锚节点的总数。

将得到的锚节点平均每跳距离误差来修正锚节点平均每跳距离Hi，可得出修正后的每个锚节点的平均每跳距离。

最后在利用极大似然估计法定位时当选择所有锚节点作为未知节点的参考锚节点，其平均定位误差并不会达到最小误差的结果，而是选择其中离未知节点较近的一部分锚节点作为参考节点会有更好的效果，这时得到的估计距离是最接近实际距离的。本文改进的算法定位精度相对提高，为了更直观，表1列出了本文算法与几种改进算法的部分数据比较。

表1 不同算法的部分数据比较m

4 实验结果及分析

为了验证改进后算法的性能，利用Matlab对本文改进的算法与其他算法进行仿真对比，对比其定位精度。在100 m×100 m的无线传感器网络环境中，且仿真结果数据均取自30次仿真的平均值。分别对算法中未知节点数目、锚节点所占比例、节点通信半径三个参数变化时，定位误差是如何变化的进行仿真分析。为了便于比较，使用统一的评价标准为平均定位误差，并对其做通信半径归一化处理。其定义式为：

（1）未知节点数目对定位误差的影响

仿真环境为锚节点数目20，节点通信半径为30 m，通过改变未知节点数量，观察对定位算法误差的影响。

由图2可知，随着未知节点个数的不断增加，各种算法的平均定位误差均大幅度下降，改进的算法要比其他算法下降幅度大。未知节点到达120之后，误差下降的幅度逐渐趋于平缓、稳定。因为随着未知节点数的增加，节点之间联系更加紧密，加强了网络的连通性。

图2 未知节点与定位误差关系

（2）锚节点比例对定位误差的影响

节点总数200，节点通信半径R分别为30 m、20 m、15 m三种情况下，观察锚节点比例对平均定位误差的影响。

图3是当节点通信半径为30 m时，锚节点数量的增加与平均定位误差的关系图。从图中可以明显看出，随着锚节点个数的不断增加，定位误差均呈现降低的趋势。但是，当锚节点的数量相同时，本文提出的算法下降速度要快于其他算法。

图3 锚节点与平均定位误差关系图（R=30）

图4和图5是当节点通信半径为20 m和15 m时，锚节点数量的增加与算法平均定位误差的关系图。均是随着锚节点数量的增加，所有算法平均定位误差迅速下降，下降到一定程度趋于平缓，改进的算法要比其他算法下降得快。

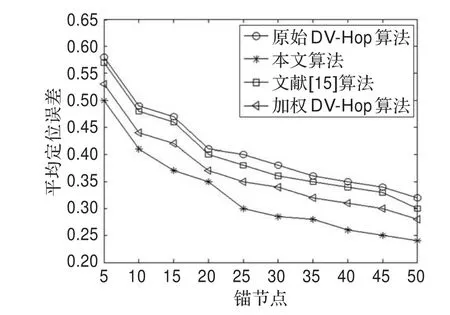
图4 锚节点与平均定位误差关系图（R=20）

图5 锚节点与平均定位误差关系图（R=15）

（3）不同通信半径下，本文算法平均定位误差关系

图6是在不同的通信半径下，改进算法的误差随锚节点的变化情况。随着节点通信半径的增加，锚节点的增加平均定位误差均明显下降，且通信半径为30 m时，算法性能最好，定位误差最低。

图6 不同通信半径下，本文算法平均定位误差关系图

5 结束语

本文对DV-Hop无线传感器网络节点定位算法进行了研究，首先简单介绍了原始DV-Hop算法流程，并简要分析了算法的不足。提出了一种多功率锚节点辅助定位方法，使用不同发射功率来控制锚节点传输不同的通信半径，保证了1跳之内节点间距离更加精确，进一步为校正值选取提供了可靠的数据，并且对DV-Hop算法本身的参数进行优化，最后对改进算法进行仿真。仿真结果显示，本文提出的算法其性能更好，有效地提高了算法的定位精度，网络节点覆盖率，算法的适应性更强。

[1]赵灵锴，洪志全.基于无线传感器网络的DV-Hop定位算法的改进[J].计算机应用，2011，31（5）：1189-1192.

[2]Qiu R C，Zhang Changchun，Hu Zhen，et al.Towards a largescale cognitive radio network tested spectrum sensing system architecture and distributed sensing[J].Journal of Communications，2012，7（7）：552-566.

[3]Chen Xiaoyan，Pei Yanli.The application of QGA in sensor optimization design[C]//Proc of the 6th International Conference on Distributed Computing and Applications for Business，Engineering and Sciences，Wuhan，China，2007：14-17.

[4]Shihong Duan，Yadong Wan，Zhiqiang Guo，et al.RAAH：Reliability Aware Adaptive Hopping scheme on timevarying channel model in WSN[J].JCIT，2013，8（1）：16-25.

[5]胡斌，立方敏.基于RSSI量化模型的定位算法研究[J].武汉理工大学学报，2009，31（23）：92-95.

[6]刘少飞，赵清华，王华奎.基于平均跳距估计和位置修正的DV-Hop定位算法[J].传感技术学报，2009，22（8）：1154-1158.

[7]王书锋，侯义斌，黄樟钦.无线感知网络最小二乘法定位算法的误差分析与优化[J].系统仿真学报，2009，21（19）：6211-6215.

[8]Qiu Lele，Hu Yanjun，Wang Yi，et al.A novel multimedia transmissionmethodbasedonquantizedcompressive sensing for Wireless Sensor Network[J].IJACT，2013，5（1）：496-504.

[9]Zhao Chanchan，Hai Xiaowei，Jiang Xiaohua，et al.Coal mine environment monitoring with Wireless Sensor Networks[J].IJACT，2013，5（1）：505-514.

[10]He T，Huang C，Blum B M，et al.Range-free localization schemes for large scale sensor networks[C]//Proceedings of the 9th Annual International Conference on Mobile Computing and Networking.San Diego：ACM Press，2003： 81-95.

[11]张震，闫连山，刘江涛，等.基于DV-Hop的无线传感器网络定位算法研究[J].传感技术学报，2011，24（10）：1469-1472.

[12]王丽侠.无线传感器网络中DV-Hop算法的研究及改进[J].唐山学院学报，2013，26（3）：75-78.

[13]王颖，石昊旸.改进的无线传感器网络DV-Hop定位算法[J].计算机工程，2012，38（7）：66-69.

[14]Wang Guo，Juan Wei.Optimization research of the DVHop localization algorithm[J].TELKOMNIKA Indonesian Journal of Electrical Engineering，2014，12（4）：2735-2742.

[15]顾亦然，蒋璐璐.无线传感器网络定位算法研究[D].南京：南京邮电大学，2012：23-30.

TAO Zhiyong,WEI Qiang,LIU Ying

School of Electronic and Information Engineering,Liaoning Technical University,Huludao,Liaoning 125105,China

In wireless sensor networks,aiming at the default that DV-Hop localization algorithm has large errors in the calculation of the distance of unknown node to an anchor node and the jump distance of the adjacent nodes in the communication radius,this paper presents an auxiliary anchor node distributed localization algorithm.This algorithm does not require any ranging technical support.It uses the power control of the anchor nodes by sending the beacon signals with different transmit powers,and the unknown nodes which receive the beacon signals will record the beacon information.It uses whole network anchors to fix separate anchor nodes on per hop distance,and then calculates the coordinates of nodes with great natural method.The Matlab simulation results show that in the same network environment,this algorithm can effectively reduce positioning errors caused by distance calculation and is suitable for the actual situation with high accuracy.

Wireless Sensor Networks（WSN）;node location;anchor;average hop distance;maximum likelihood method; Distance Vector（DV）-Hop algorithm

A

TP393

10.3778/j.issn.1002-8331.1403-0101

TAO Zhiyong,WEI Qiang,LIU Ying.Improved DV-Hop localization algorithm based on more power auxiliary anchor nodes.Computer Engineering and Applications,2014,50（21）：121-124.

辽宁工程技术大学研究生学院第五届科研立项（No.5A2014029-01）。

陶志勇（1978—），男，博士研究生，副教授，主要研究方向：无线传感器网络、多媒体通信；魏强（1988—），男，通讯作者，硕士研究生，主要研究方向：无线传感器网络；刘影（1983—），女，博士研究生，主要研究方向：无线传感器网络。E-mail：1102773015@qq.com

2014-03-11

2014-04-26

1002-8331（2014）21-0121-04

CNKI出版日期：2014-07-02，http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1403-0101.html