基于DSmT的DEMATEL改进新方法

杜元伟，杨娜

昆明理工大学管理与经济学院，昆明 650093

基于DSmT的DEMATEL改进新方法

杜元伟，杨娜

昆明理工大学管理与经济学院，昆明 650093

原始DEMATEL方法及其改进方法，一方面存在因正规化影响矩阵的无穷次幂可能并不收敛而导致方法在某些情况下失效的问题，另一方面也存在因语言标度之间并不相互独立而不能使用Dempster规则对专家推断信息进行直接融合的问题。为了解决上述问题，以Lee和Tzeng提出的改进DEMATEL方法为研究对象，结合语言评估标度和证据理论中的基本信度分配函数构建了具有柔性表达优势的专家推断信息提取机理，通过引入DSmT组合规则提出了能够对所有专家推断信息进行有效集成的融合机理，并在此基础上给出了DEMATEL改进新方法的具体步骤，应用一个模拟案例分析了提出的方法更具科学性和普适性。

决策试行与评价实验室（DEMATEL）方法；语言评估标度；基本信度分配；DSmT组合规则；三角模糊数

1 引言

DEMATEL（决策试行与评价实验室）方法是由美国学者Fontela提出的一种运用图论与矩阵论原理进行系统因素分析的方法。它通过专家打分等方式找出系统因素之间的影响关系并表示为直接影响矩阵，计算综合影响矩阵获取因素中心度、原因度，进而得到因素所属种类（原因因素或者结果因素）并给出相应管理建议。该方法能够借助专家知识、经验、直觉找到系统中的关键因素，已被广泛地应用于解决营销策略、控制系统、安全问题以及群决策等领域中的问题[1-2]。特别地，近几年来，专家学者们从不同学科视角对该方法进行了理论改进和应用研究。如：Liou通过模糊偏好规划算法集成多专家意见并以此改进DEMATEL方法[3]；胡伟等针对DEMATEL方法仅将系统要素简单划分为原因要素和结果要素存在的应用缺陷，通过实施逐层分级构建了多级递阶改进方法[4]；Wu等将模糊集理论与DEMATEL方法相结合，基于人性模糊判断研究了全球性管理者必需的技能要素[5]；Buyukozkan等基于DEMATEL方法和网络分析法的联合技术开发出一种用于确定企业关键六西格玛项目及相应优先次序的方法[6]。可以看出，专家学者们大多是从个体层面对DEMATEL方法开展改进研究，而对于群体层面的研究成果却并不多见。虽然已有个别学者尝试着应用证据理论中的Dempster规则融合由多位专家给出的不精确、不完备形式的意见[3，7]，但其中仍存在以下两方面问题。其一，改进的对象仍是原始DEMATEL方法，但原始方法已被证明本身存在着固有理论缺陷——正规化影响矩阵的无穷次幂可能并不收敛而造成在某些情况下方法失效；其二，表达因素之间关系及其影响程度的方法同原始方式一样采用的是“强→3、中→2、弱→1”形式的语言标度赋值，但并未考虑人类语言的先天不精确性使得语言标度之间并不相互独立（如：考虑该种语言的不精确性后，强→（0.5，0.7，1.0），中→（0.3，0.5，0.7），弱→（0.0，0.3，0.5），即三者之间可能存在交叉、不独立，详见后文），从而导致了不能直接应用Dempster规则对专家意见进行合成（该规则应用的前提是识别框架中元素之间彼此独立）。有鉴于此，本文将Lee和Tzeng针对DEMATEL方法固有缺陷提出的改进方法[8]作为研究对象，基于DSmT理论构建一种能够对多位专家以语言标度形式给出的且允许其中存在不精确性、不完备性的推断信息进行科学融合的DEMATEL改进新方法。

2 方法步骤及Lee/Tzeng改进原理

原始DEMATEL方法的整个运算过程可以划分为以下五个步骤[2，8-9]。

步骤1确定系统影响因素集合。设系统有N个因素，形成影响因素集合L={Ln|n=1，2，…，N}。

步骤2确定因素关系并构建直接影响矩阵。假设专家结合自身知识、经验、直觉给出所有因素之间有无直接影响关系的判断，并通过专家打分方式给出因素之间具体影响程度值（强→3、中→2、弱→1），在此基础上构建初始直接影响矩阵A=[aij]N×N。

步骤3计算综合影响矩阵。将初始直接影响矩阵A进行标准化处理得到正规化影响矩阵为：并按T=D+D2+…+D∞计算各因素受其他因素直接和间接影响后的综合影响矩阵。当α→∞时，Dα收敛为零矩阵，即为综合影响矩阵，其中I为单位矩阵。

步骤4计算因素中心度和原因度。计算综合影响矩阵T中各行之和得到相应因素的影响度Tr，计算各列之和得到相应因素的被影响度Tc。由Tr+Tc、Tr-Tc计算代表各因素在系统中所起作用大小的中心度和表示因素之间结构关系的原因度。

步骤5确定关键影响因素并提出管理建议。为使系统复杂性维持在可管理的水平上，必须保证最终得到系统因素之间的影响关系具有显著性，因此通过对综合影响矩阵T设置阈值P0过滤掉影响程度值（中心度）小于阈值P0的微弱因素关联。筛选出系统关键因素之后，根据其原因度的正负提出相应管理建议。

特别地，当专家个数不止一人时，设由专家Eh构建的直接影响矩阵为合所有专家推断的初始直接影响矩阵A=[aij]N×N中的元素一般由式（2）予以确定。

需要说明的是：Lee和Tzeng则认为上述原始DEMATEL方法在步骤3求解综合影响矩阵的过程中利用了潜在假设条件，而该假设并不是在任何情况下都成立。为此，他们提出了只有当正规化影响矩阵A中每一列的和均小于1时，经归一化处理之后得到的正规化影响矩阵的无穷次幂才会收敛于零矩阵的定理，但是，只要其中有一列之和等于整数1，则可能收敛也可能不收敛。也就是说，当在没有收敛为零矩阵时，T=D+D2+…+D∞将不存在，更不会有T=D(I-D)-1，此时DEMATEL方法将失效。针对上述问题，Lee和Tzeng在文献[8]中提出了在求解正规化影响矩阵的过程中引入一个很小的正数ε（如10-5），由此经归一化处理后得到改进的正规化影响矩阵为：

3 专家推断信息提取机理

专家针对系统因素之间影响关系及其影响程度给出的推断信息有效程度决定了应用DEMATEL方法识别系统关键因素的优劣程度，这也是该方法的关键所在。然而，受专家有限知识结构、专业水平、对评判对象的了解程度等诸多因素的限制，试图令所有专家都给出精确的、完备的推断信息并不现实（即便勉强给出所有信息，其中也必然存在诸多错误之处）。而更为可行的方式是认识到专家主观推断能力有限的客观现实，允许专家用自己的语言表达对于因素之间影响程度强弱的真实推断（就是把问题中涉及的评估变量看成是语言短语而不是数字值，用更直接有效形式表达那些不能准确表达的信息[10]），承认推断信息中存在不精确性和不完备性。其中：不精确性体现在，语言标度向具体数值转换时可能存在着相互交叉而非完全独立；不完备性体现在，专家给出的推断信息允许存在着“不知道”或者“不完全知道”。

设专家Eh欲针对因素Li对Lj的影响程度做出推断，赋值方式遵循DEMATEL方法中的弱(s1)、中(s2)、强(s3)三个级别，另将无影响（影响程度为0）视为s0。专家在推断过程中可能存在以下三种情形。情形1：若Eh是一位业界权威、资深的专家，其对该问题认识极其深刻，能够明确地判断出Li对Lj有直接影响且影响程度为sk，k∈{0，1，2，3}。情形2：若Eh是一位其他领域的专家，且对该问题完全没有概念，则其应该实事求是地给出推断信息——“不知道”，否则即便其勉强给出了相对具体的信息（可以理解为错误信息或者是噪声信息），而这对于解决该问题而言不仅毫无价值而且还会有负面影响。情形3：若Eh的资历不深但也有一定的专业经验，虽然无法给出完全明确的推断信息，但也不至于完全不知道，故其结合自身认识程度所给出的应该是类似于不确定推断信息，即影响程度可能是sk′或sk″中的一个（可能程度假设为80%），其他情况为不知道，该种情形也是更为一般、普遍的。

在上述三种情形中，前两种显然是第三种的特例，而第三种恰与DSmT理论（Dezert-Smarandache Theory）中基本信度分配（Basic Belief Assignment，BBA）的定义完全相符。DSmT作为DS证据理论的延伸和发展，是一种用来处理不确定性多源推理问题的信息融合技术。它通过BBA函数描述不确定、不完备信息，融合不同来源的证据信息却并不要求识别框架内元素之间的相互独立性，其优势在于既能处理多源证据信息的不精确性、不完备性，又能在高冲突的情况下得到比DS证据理论更加合理的融合结果[11]。显然，本文中语言评估标度集合Θ={sk|k=0，1，2，3}即构成了评价影响程度的识别框架Θ，而由专家针对因素之间关系及其影响程度推断所给出的实际语言评估标度可能是识别框架Θ中的某个或某些元素。由Θ中任意元素的交集、并集组成的集合形成超幂集DΘ，不妨设超幂集DΘ内任意非空子集为A，A的可信程度为m(A)。若映射函数m:DΘ→[0，1]满足BBA函数。特别地，当m(A)＞0时称A为焦元。遵循BBA函数的基本原理，前文中情形1可表示为m(sk)=1，情形2可表示为m(Θ)=1，情形3可表示为m(sk′，sk″)=0.8且m(Θ)=0.2。由此可见，专家基于语言标度所给出的不精确性、不完备性推断信息能够由BBA函数予以有效地表达。

需要说明的是：由于专家都是经过事先慎重挑选的，因而一般不会出现某位专家无法给出任何判断信息，或者说完全不知道识别框架中哪个或哪几个语言评估标度可能是因素之间关系及其影响程度（即第二种情形，即m(Θ)=1），倘若万一在推断过程中出现了该种情形，则可以考虑将该专家更换为其他更有经验的专家。

4 专家推断信息融合机理

本文采用语言标度和BBA函数提取每位专家对因素之间关系及其影响程度判断的推断信息，而他们的推断信息之间可能并不相同甚至相互冲突，所以只有对这些推断信息进行融合并将结果转化为具体数值才能将其应用于DEMATEL方法之中。如前文所述，语言标度先天具有不精确性，故许多专家学者建议采用三角模糊数实现由语言形式向数值形式的转化。

因为DEMATEL方法采用的是强、中、弱、无四个级别对影响程度进行赋值，所以这里给出对应于语言标度且以三角模糊数表示的隶属函数[10]（如表1所示）。

表1 语言评估标度与三角模糊数对应关系

由表1可知，相邻语言标度之间并不独立而是存在一定的交叉性，因而预设语言评估标度集合Θ={sk|k= 0，1，2，3}中各元素存在相容性，故不能采用DS证据理论的Dempster组合规则对专家推断信息进行融合。庆幸的是，DSmT理论并不要求识别框架内元素具有独立性，可以借鉴该理论中的组合规则（称之为DSmT组合规则）对各专家以语言标度形式给出的BBA函数进行融合。具体而言：设针对因素Li对Lj关系及其影响程度的推断问题，由专家E1和Eh以语言标度方式给出的BBA函数形式的推断信息为m1和m2，则融合两个专家推断信息的DSmT组合规则为：

其中，B1和B2分别是m1和m2中焦元所对应的三角模糊数。

应用式（5）对所有专家的推断信息开展两两合成并在多次迭代后可以计算出融合所有专家推断信息的

其中，λ∈[0，1]为风险偏好系数，反映专家组的风险态度。当λ＞0.5时，表示专家组是风险追求型的；当λ＜0.5时，表示专家组是风险厌恶型的；当λ=0.5，表示专家组是风险中立型的。由此得到的Gij即为由专家组最终给出的因素Li对Lj的影响程度推断值。

5 改进新方法步骤

专家推断信息提取机理和融合机理均是针对因素Li对Lj关系及其影响程度问题构建的，所得到的结果仅是初始直接影响矩阵中的一个元素数值。下面在上述两种机理的基础上，结合Lee和Tzeng提出的改进原理，给出DEMATEL改进新方法的具体步骤。

步骤1前期准备。确定系统因素集合L={Ln|n= 1，2，…，N}，并将语言评估标度构成的集合Θ={sk|k=0，1，2，3}作为评价该问题的识别框架。结合问题性质及特征，选定相关领域专家E1，E2，…，EH，并由专家组确定风险偏好系数λ。因为系统中共有N个因素且任意两个因素之间的影响程度仅需判断一次，故在直接影响矩阵的构建过程中共有N(N-1)/2个影响程度问题需要推断。不妨设需要推断的问题为Δr，r=1，2，…，R，R=N(N-1)/2。

步骤2令r=1。

步骤3专家针对推断问题给出推断信息。邀请每位专家结合自身知识、经验、直觉，按照规定语言标度给出以BBA函数形式存在的推断信息（允许存在不精确性、不完备性，详见专家推断信息提取机理）。不妨设由专家Eh针对推断问题Δr给出的推断信息为，h= 1，2，…，H。

步骤4融合所有专家给出的推断信息。先将由步骤3得到的专家推断信息(h=1，2，…，H)中的焦元按照表1转化为三角模糊数形式，再利用DSmT组合规则实现所有专家推断信息的融合，得到综合BBA函数值m(r)，最后结合式（5）计算数学期望Gr，该值即为当前推断问题的影响程度。

步骤5令r=r+1。若r≤R，说明还存在需要推断的问题，转步骤3；若r＞R，说明已完成全部推断，此时依据G1，G2，…，GR构造出直接影响矩阵，并转步骤6。

步骤6计算综合影响矩阵并确定关键因素。将直接影响矩阵带入第2章中的步骤3～步骤5，即可计算出综合影响矩阵，在此基础上依据中心度和原因度就能确定出系统关键因素。需要特别强调的是，在计算正规化直接影响矩阵时，应遵循由Lee和Tzeng提出的改进方法，通过引入一个很小的正数ε并按照式（3）进行计算。确定关键因素之后，就可以根据因素的性质给出相应管理建议。

6 案例模拟分析

结合文献[12]中的案例，利用本文方法模拟分析金融人才职业能力素质的关键因素。影响因素分别为：进取心(L1)、持续学习(L2)、责任心(L3)、沟通能力(L4)、团队合作能力(L5)、解决问题能力(L6)、学习背景(L7)、专业知识(L8)、工作经验(L9)；在相关领域选定专家为E1，E2，…，E5。因为共有9个因素，故需要推断的问题个数为R=N(N-1)/2=36个。

限于篇幅，仅以因素L1对因素Lj(j=1，2，…，9)的关系及其影响程度推断为例，进行模拟求解。设五位专家各自推断出的因素L1对Lj(j=1，2，…，9)的影响程度信息如图1所示，将图1中五位专家给出的BBA函数代入本文方法步骤4，计算L1对Lj(j=1，2，…，9)的影响程度，详见式（7）第1行。类似地，可以计算得到其他推断问题的影响程度结果。将所有计算得到的影响程度进行组合便可得到金融人才职业能力素质所有影响因素的直接影响矩阵，参见式（7）。

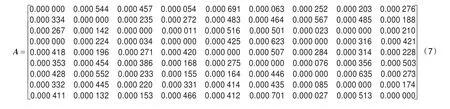
图1 专家对L1→∀Lj给出的推断信息

在此基础上，按照本文方法步骤6，求解矩阵A中各列元素之和并取最大值，并通过引入ε=10-10计算标准化直接影响矩阵X和综合影响矩阵S，具体如式（8）和式（9）所示。

由此可见，本文方法采用语言标度和BBA函数能够有效地描述专家给出的不精确性、不完备性推断信息，并可以对所有推断信息进行科学融合，从而实现关键因素的有效识别。相对于现有方法而言，本文方法一

通过计算因素中心度实现因素{L1，L2，…，L9}的重要性排序，并根据因素原因度提出因素控制的相应管理建议。上述信息具体如表2所示。方面因为提取的专家推断信息更加真实而使最终结果更具科学性，另一方面也因采用Lee和Tzeng改进方法进行正规化矩阵求解而更具普适性。

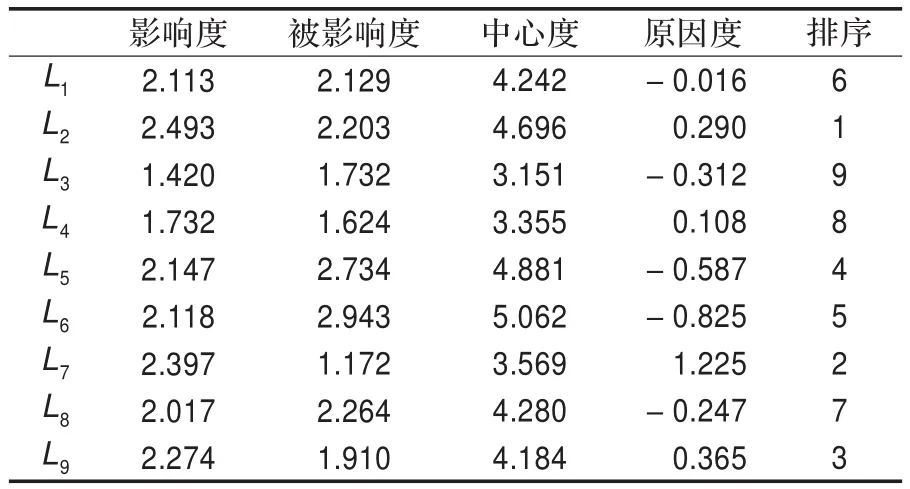
表2 系统各因素中心度、原因度及重要性排序

7 结束语

原始DEMATEL方法及其改进方法存在着以下两方面问题。其一，因正规化影响矩阵的无穷次幂可能并不收敛而导致方法在某些情况下失效；其二，因语言标度之间并不相互独立而不能使用Dempster规则对专家意见进行直接融合。为此，本文以Lee和Tzeng提出的改进DEMATEL方法为研究对象，结合语言评估标度和DSmT理论中的BBA函数构建了具有柔性表达优势（能够描述推断信息中的不精确性、不完备性）的专家推断信息提取机理，然后通过引入DSmT组合规则提出了能够对专家意见进行有效融合的专家推断信息融合机理，在此基础上给出了DEMATEL改进新方法的具体步骤。最后应用一个模拟案例分析了提出方法的科学性和普适性。需要说明的是：其一，本文遵循DEMATEL方法中采用的“强”、“中”、“弱”、“无”的语言标度等级描述因素之间的影响程度，而随着对推断结果精确性要求的提高，亦可考虑采用更多等级的语言标度进行描述（如：强、较强、中、较弱、弱、无），此时仅需将这些语言标度集合视为识别框架并根据相关理论将语言标度转化为相应三角模糊数值即可。其二，本文将所有专家视为同等重要，并没有考虑专家之间因权威度、知识经验等方面的差异而带来的推断信息可靠性有所不同的问题，若因客观现实需要考虑这个问题时，仅需先利用折扣因子（专家权重相对于最权威专家权重的比值）对每位专家给出的推断信息进行处理后，再代入本文方法步骤6即可。

[1]Liou J J H，Yen L，Tzeng G H.Building an effective safety management system for airlines[J].Journal of Air Transport Management，2008，14（1）：20-26.

[2]Liou J J H，Tzeng G H.A causal analytical method for group decision-making under fuzzy environment[J].Expert Systems with Applications，2008，34（1）：205-213.

[3]Liou J J H.Developing an integrated model for the selection of strategic alliance partners in the airline industry [J].Knowledge-Based Systems，2012，28：59-67.

[4]胡伟，程幼明.DEMATEL的改进及其在供应链失效分析中的应用[J].统计与决策，2013（6）：83-86.

[5]Wu Weiwen，Lee Yuting.Developing global managers’competencies using the fuzzy DEMATEL method[J].Expert Systems with Applications，2007，32（2）：499-507.

[6]Buyukozkan G，Ozturkcan D.An integrated analysis approach for six sigma project selection[J].Expert Systems with Applications，2010，32（8）：5835-5847.

[7]李亚群，段万春，孙永河，等.基于证据理论的群组DEMATEL改进方法[J].计算机工程与应用，2013，49（20）：9-14.

[8]Lee H S，Tzeng G H，Yeih Weichung，et al.Revised DEMATEL：resolving the infeasibility of DEMATEL[J]. Applied Mathematical Modelling，2013，37（10）：1-12.

[9]Tzeng Gwo-Hshiung，Chiang Cheng-Hsin，Li Chung-Wei. Evaluating intertwined effects in e-learning programs：a novel hybrid MCDM model based on factor analysis and DEMATEL[J].Expert Systems with Applications，2007，32（4）：1028-1044.

[10]徐泽水.基于语言标度中术语指标的多属性群决策法[J].系统工程学报，2005，20（1）：84-88.

[11]Dezert J，Smarandache F.An introduction to DSmT in information fusion[J].Broad Research in Artificial Intelligence and Neuroscience，2011，1：1-64.

[12]刘安英，魏法杰.基于改进语言评估标度的专家后验权重确定方法研究[J].中国管理科学，2011，19（6）：149-154.

DU Yuanwei,YANG Na

Faculty of Management and Economics,Kunming University of Science and Technology,Kunming 650093,China

There exist two problems in original and improved DEMATEL methods.One is methods may fail under some circumstances for the infinite power of a normalized relation matrix may not converge,and the other is the Dempster rules cannot be used to make direct fusion of experts’inferences due to the independence of language scales.To solve the above two problems,the experts’inferences extraction mechanism with the advantage of soft expression is constructed based on language evaluation scales and the basic belief distribution function by taking the DEMATEL improvement method proposed by Lee and Tzeng as the research subject.By introducing DSmT combination rule,the fusion mechanism is suggested which can be used to make effective integration of all experts’inferences,based on which,the procedures of the new method for improvement of DEMATEL are suggested.The analysis of a simulation case is made to prove the proposed method is more of science and universality.

Decision Making Trial and Evaluation Laboratory（DEMATEL)method;language assessment scales;basic probability assignment;DSmT combination rule;triangular fuzzy number

A

C934

10.3778/j.issn.1002-8331.1402-0008

DU Yuanwei,YANG Na.New improved DEMATEL method based on DSmT.Computer Engineering and Applications,2014,50（21）：68-73.

国家自然科学基金（No.71261011，No.71462022）；云南省应用基础研究计划项目（No.2011FZ021，No.2013FB030）；云南省教育厅重点项目（No.2012Z103）；云南省哲学社会科学创新团队建设项目资助（No.2014cx05）。

杜元伟（1981—），男，博士/博士后，教授/硕士生导师，研究方向为管理决策、信息融合等；杨娜（1988—），女，硕士生，研究方向为管理决策。E-mail：duyuanwei@gmail.com

2014-02-07

2014-03-22

1002-8331（2014）21-0068-06

CNKI出版日期：2014-06-18，http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1402-0008.html