元胞自动机交通流NS模型相图研究
朱昶胜,王兵,黄军强,王杰
1.兰州理工大学计算机与通信学院,兰州 730050
2.中国人民解放军69064部队
3.中国人民解放军69065部队
元胞自动机交通流NS模型相图研究
朱昶胜1,王兵1,黄军强2,王杰3
1.兰州理工大学计算机与通信学院,兰州 730050
2.中国人民解放军69064部队
3.中国人民解放军69065部队
基于开放边界条件下元胞自动机交通流NS模型,模拟入口概率α、出口概率β、车辆最大速度Vmax以及随机慢化概率ρ对系统流量J的影响,根据不同流相中流量J的变化规律,建立NS模型的相图。结果表明,车辆最大速度在一定范围内的增加能提高系统流量,车辆的随机慢化概率在小于临界随机慢化概率ρc时,不会对系统流量造成影响,而超过ρc时,随机慢化概率越大,对系统流量的反作用越明显。Vmax和ρ决定系统相图。当Vmax=5,ρ<ρc时,系统相图只由自由流相和堵塞流相构成,自由流相和堵塞流相被一条曲线分开;ρ>ρc时,最大流相出现,最大流相区域随着ρ增大而增加。
元胞自动机;交通流;流量;相图
1 引言
交通问题的研究是一个多学科交叉的研究领域,它与物理学,尤其是统计物理学有着密切的关系,例如当汽车密度由低到高增加到一个临界值时,高速公路上的车流会从自由运动相转化成堵塞相,这正是近代物理学中所关注的自组织临界性和相变行为[1]。交通流理论最早在20世纪30年代就被提出来了,随着交通运输业的高速发展和计算机技术的引入,交通流理论得到了很大的发展。目前,交通流理论既有考虑总体流动性的宏观模型,如流体动力学模型、气体动力论模型,也有考虑单一车辆行为的微观模型,如车辆跟驰模型、元胞自动机模型[2]。
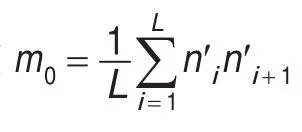
2 模型简介
NS模型是典型的一维交通流CA模型,适用于高速公路基本路段的交通流模拟,该模型的模拟结果与实际情况较为吻合,因此,获得了广泛的应用和借鉴,以后很多模型都是基于NS模型的。该模型用长度为L的一维离散的格点链来模拟道路,每一格点在某一时刻或者被一个车辆占据,或者为空,数组Xn(t)表示第n辆车在t时刻在格点链上的位置,数组Vn(t)在{0,1,…,Vmax}的Vmax+1个取值范围内取其中一个整数值,Vmax表示车辆能达到的最大速度,模型中时间和空间均为离散,dn(n)=Xn+1(t)-Xn(t)表示第n辆车在t时刻与前方最近邻车辆之间的间隔。在每个时间间隔t→t+1,NS交通流模型的基本演化过程分为加速过程、减速过程、随机慢化过程和位置更新。

图1 车辆最大速度对流量的影响

开放边界条件[15]定义如下:每个时步以入口概率α在车道入口产生一辆速度取最大数值的车辆,参加演化,若其不动,则消除这辆车;每个时步在道路出口车辆以出口概率β驶出系统。
3 数值模拟结果与分析

3.1 车辆最大速度对流量的影响
图1显示了车辆最大速度Vmax对流量J的影响。
图1(a)是在出口概率β=1、随机慢化概率ρ=0.5时,车辆最大速度Vmax对流量的影响。由图1(a)可以看出,Vmax≤5时,系统流量随着Vmax增大而增加;当Vmax>5时,Vmax的增大不会对流量产生影响。从而验证了高速公路设置最低时速和最高时速的合理性。当入口概率α<0.35时,流量随着入口概率的增大而增加,符合自由流相的主要特征;当α>0.35时,流量维持稳定状态,系统进入最大流相。有趣的是,当Vmax≥5时,系统从自由流进入最大流时,流量会突然增大,这种现象随着车辆最大速度的增大而愈发明显。
图1(b)是在入口概率α=1、随机慢化概率ρ=0.5时,车辆最大速度Vmax对流量的影响。由图1(b)可以看出,在出口概率β取值较低时,流量随着β的增大而增加,此时系统处于自由流相。而当β增大的一定值时,流量会趋于稳定,系统从而达到最大流相。随着Vmax的增大,系统进入最大流相时对应的β值也在增加。当Vmax=2时,对应的β=0.8;Vmax=3时,对应的β=0.85;Vmax=4时,β=0.87;Vmax≥5时,β=0.89。
3.2 随机慢化概率对流量的影响
图2显示了随机慢化概率ρ对流量J的影响。
图2(a)是在出口概率β=1,车辆最大速度Vmax=10(Vmax=5类似)时,随机慢化概率ρ对流量的影响。
由图2(a)可以看出,当入口概率α确定时,系统流量随着随机慢化概率ρ的减小而增加。当ρ=0,α≈0.8时,流量达到一个单顶峰,说明系统的最大流相只是一个点,相图由自由流和堵塞流构成。但是当ρ=0,α>0.8时,流量值随着α的增加反而会降低,此时对应相图中的堵塞流相。类似的现象也出现在ρ=0.125的曲线中。而当ρ>0.125时,系统的自由流和最大流之间的界线愈发明显。自由流相区域随着ρ的增大而减小,最大流相的区域随着ρ的增大而增加。
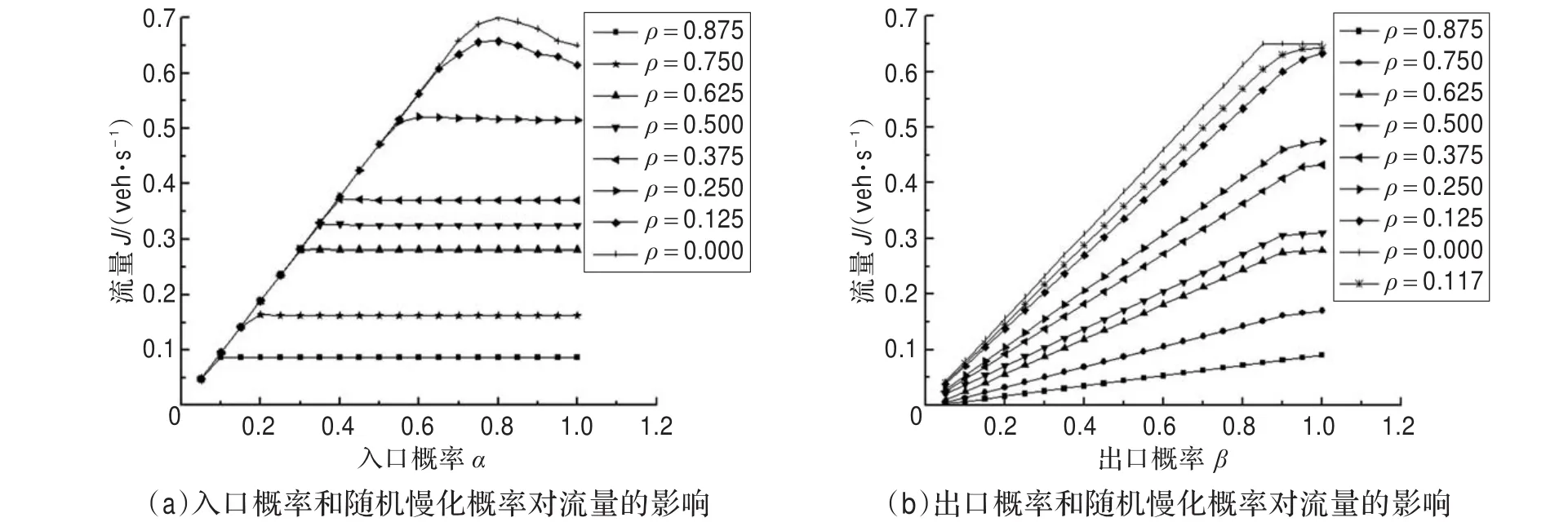
图2 随机慢化概率对流量的影响
图2(b)是在入口概率α=1,车辆最大速度Vmax=5时,随机慢化概率ρ对流量的影响。由图2(b)可以看出,当出口概率β确定时,系统流量随着随机慢化概率ρ的减小而增大。当ρ=0时,随着β的增大,系统流量没有发生变化,说明此时β已经不是制约系统流量的参数,系统由堵塞相进入自由流相。随着ρ的增大,系统进入最大流相时对应β≥0.8的β值增大。当ρ>ρc时,系统最大流相消失。经过计算机精确模拟,ρc≈0.117。
3.3 相图
根据不同相下系统流量和入口概率、出口概率的关系:自由流相中流量由入口概率决定,随着入口概率的增加而增加;堵塞流相中流量由出口概率决定,随着出口概率的增加而增加;最大流相中流量值和入口概率、出口概率无关。结合所测流量数据,构建了NS模型不同Vmax、ρ下的相图。如图3所示。
图3中I区表示自由流相,II区表示堵塞流相,III区表示最大流相。
图3(a)是Vmax=2,ρ=0.5时系统的相图。系统分为三个相,三相交汇点的入口概率和出口概率分别为0.35和0.8。

图3 NS模型相图
图3(b)是Vmax=5,ρ=0.5时系统的相图。和图3(a)不同之处在于,相图I区和II区之间被一条曲线隔开。系统自由流相“侵占”了堵塞流相,由于道路车速的增加,减小了出现堵塞现象的概率。三相交汇点的入口概率和出口概率分别为0.35和0.89。Vmax=3,4时系统相图与图3(a)定性类似。
图3(c)是Vmax=5,ρ=0,0.117,0.25,0.5时系统的相图。当ρ<ρc≈0.117时,系统相图由自由流相和堵塞流相组成,说明道路中车辆不确定性减速的概率较小时,对交通产生影响较小;当ρ>ρc时,最大流相开始出现,并随着ρ的增大而区域增大。说明道路中车辆不确定性减速的概率较大时,对交通产生影响较大。
4 结论
文章基于开放边界条件下元胞自动机交通流NS模型,研究了系统车辆最大速度Vmax和随机慢化概率ρ对系统流量的影响。计算机模拟结果表明:Vmax和ρ均对系统流量产生影响,在不同Vmax和ρ下,根据系统流量与入口概率α,出口概率β关系,将系统划分不同相区,建立相图。发现车辆最大速度在一定范围内的增加能提高系统流量,验证了高速公路设置最低时速和最高时速的合理性;车辆的随机慢化概率在小于临界随机慢化概率时,不会对系统流量造成影响,而超过临界随机慢化概率时,随机慢化概率越大,对系统流量的反作用越明显。
[1]Kerner B,Rehborn H.Experimental properties of phase transitions traffic flow[J].Phys Rev Lett,1997,79(20):4030-4033.
[2]ChowdhuryD,SantenL,Schadschneider A.Statistical physics of vehicular traffic and some related systems[J]. Physics Report,2000,329.
[3]Wolf D.Cellular automata for traffic simulations[J].Physica A,1999,263:438-451.
[4]Schadschneider A.Traffic flow:a statistical physics point of view[J].Physica A,2002,313:153-187.
[5]Chopard B,Droz M.Cellular automata modelling of physical systems[M].Cambridge:Cambridge University Press,1998.
[6]Biham O,Middleton A,Levine D.Self-organization&a dynamic transition in traffic flow models[J].Phys Rev A,1992,46.
[7]贾斌,高自友,李克平.基于元胞自动机的交通系统建模与模拟[M].北京:科学出版社,2007.
[8]Nagel K,Schreckenberg M.A cellular automaton model for freeway traffic[J].J Phys I(France),1992,2:2221-2229.
[9]Nagatani T.Effect of traffic accident on jamming transition in traffic flow model[J].J Phys A,1993,26:1015-1020.
[10]Benjamin S C,Johnson N F,Hui P M.Cellular automata models of traffic flow along a highway containing a junction[J].J Phys A,1996,29:3119-3128.
[11]Chung K H,Hui P M,Gu G Q.Two dimensional traffic flow problems with faulty traffic lights[J].Phys Rev E,1995,51:772-774.
[12]薛郁,董力耘,戴世强.一种改进的一维元胞自动机交通流模型及减速概率的影响[J].物理学报,2001,50(3).
[13]Gerwinski M,Krug J.Analytic approach to the critical density in cellular automata for traffic flow[J].Phys Rev E,1999,60:188-169.
[14]Eisenblatter B,Santen L,Schaadschneider A,et al.Jamming transition in cellular automaton model for traffic flow[J].Phys Rev E,1998,57:1309-1314.
[15]Tan Huili,Liu Muren,Kong Lingjiang.A study on an improved Nagel-Schreckenberg traffic flow model with open boundary conditions[J].Acta Physica Sinica,2002,51(12):2713-2718.
ZHU Changsheng1,WANG Bing1,HUANG Junqiang2,WANG Jie3
1.College of Computer and Communication,Lanzhou University of Technology,Lanzhou 730050,China
2.Unit 69064 of PLA,China
3.Unit 69065 of PLA,China
Based on the NS traffic model with open boundary conditions,the influence of the injected probabilityα,the removed probabilityβ,the maximum velocityVmaxand the randomization probabilitiesρon the flowJis simulated. Then the phase diagrams are constructed due to the change ofJin different regimes.Results show thatJcan be improved along with the increase ofVmaxwithin a certain range.Whenρis smaller than the critical randomization probabilityρc, it will not affectJ.When ρ exceedsρc,the bigger theρis,the more obvious reaction onJis.Vmaxandρdeterminate the phase diagrams.Whenρ<ρc,the phase diagram only consists of the free flow regime and the jamming regime,and the two regimes are separated by a curve.Whenρ>ρc,the maximum current occurs and it will increase with the increase ofρ.
cellular automaton;traffic flow;flow;phase diagram
A
TP391
10.3778/j.issn.1002-8331.1212-0011
ZHU Changsheng,WANG Bing,HUANG Junqiang,et al.Study on phase diagram based on NS model.Computer Engineering and Applications,2014,50(21):48-51.
国家自然科学基金(No.51161011);甘肃省科技支撑计划(No.1204GKCA065)。
朱昶胜(1972—),男,博士,教授,研究方向为智能交通系统,材料微观模拟,网络信息安全等;王兵(1986—),男,硕士,研究方向为智能交通系统;黄军强(1970—),男,工程师,研究方向为交通流仿真;王杰(1986—),男,硕士,研究方向为智能交通系统。E-mail:wbsjzc@163.com
2012-12-03
2013-01-28
1002-8331(2014)21-0048-04
CNKI出版日期:2013-02-07,http://www.cnki.net/kcms/detail/11.2127.TP.20130207.1421.021.html

