利用霍尔元件测量金属丝的弹性模量

吴高米,崔 敏,王 闯,支辛蕾,万 欣, 邓金祥,张 兵,原安娟,王丽香

(北京工业大学 应用数理学院，北京 100124)

1 引 言

弹性模量是描述固体材料抗形变能力的重要物理量，是工程技术中常用的参量[1]. 用静态法测量物体弹性模量的主要难度在于物体微小位移的测量. 传统大学物理实验教学中采用光杠杆放大法[2]进行微小位移的测量，另外，还可以利用霍尔元件来测量微小位移. 当霍尔元件[3]置于均匀梯度磁场时，由于霍尔效应，霍尔元件位置的变化将引起霍尔元件两端霍尔电压的改变，且电压与位置是一一对应关系，在特定范围内，具有良好的线性关系[4]. 本文将现有弹性模量实验仪器进行组合改装，将霍尔元件与金属丝拉伸端同步，在其周围设置均匀梯度磁场，金属丝的微小伸长量通过测量霍尔元件位置变化获得，实现了金属丝弹性模量的创新测量.

2 实验原理

设粗细均匀的金属丝的长度为L0，截面积为S，将其上端固定，下端悬挂质量为m的砝码，若金属丝受外力F的作用伸长了ΔL. 由胡克定律知，在弹性限度内，应力F/S和应变δL/L成正比[5]，即

(1)

其中，E为金属丝材料的弹性模量，其数值仅与材料性质有关，而与材料实际尺寸及外力无关. 若金属丝直径为d，则

(2)

式中，各量均为SI单位时，E的单位为Pa. 对长约65.00 cm、直径为0.8 mm的钢丝，当用1.000 kg砝码(9.8 N)竖直加力时，钢丝伸长量δL约为0.065 mm. 因此，微小伸长量的测量显得尤为重要.

霍尔元件具有结构简单、体积小、动态特性好和寿命长的优点，它不仅用于磁感应强度和电参量测量，也可进行微小位移的测量. 当霍尔元件置于磁场B中，元件内部通入激励电流I时，霍尔元件两端可产生霍尔电压UH[6]：

UH=KHIB,

(3)

其中，KH为霍尔元件灵敏度(常量)，在激励电流不变时，霍尔电压与磁场成正比.

当霍尔元件处在均匀梯度磁场中垂直于磁场方向(即实验中的竖直方向)发生微小位移时，所处磁场也发生变化，而这种变化可由霍尔电压UH显示出来. 并且，由于霍尔元件在平行于磁场方向(即实验中的水平方向)运动时磁感应强度是不变的，不会引起霍尔电压的改变，也就是说输出的霍尔电压的改变量仅由霍尔元件的竖直位移引起，因此可利用霍尔元件来测量微小位移.

3 实 验

3.1 霍尔元件位移传感定标

霍尔元件位移传感特性测试如图1(a)所示. 半导体霍尔元件(3.0 mm×2.5 mm×0.8 mm)置于2个半环形永久磁钢形成的梯度磁场中，霍尔元件通以恒定电流(精度为0.1 A). 霍尔元件通过螺旋测微头的调节在梯度磁场中上下移动，输出的霍尔电压取决于其在磁场中的位置，霍尔电压通过电压测试仪读出，霍尔元件位移量通过螺旋测微头读出.

调节霍尔元件承载装置的上下位置，使霍尔元件位于梯度磁场中间位置，此时磁场为零，霍尔电压也为零. 上下移动测微头，每变化0.05 mm读取相应的霍尔电压值，得到霍尔电压随位移变化规律如图1(b)所示. 从图中可看出，霍尔电压(精度为0.01 mV)与位移变化具有良好的线性关系，线性拟合得出UH=3.549 22x+0.013 14，灵敏度即线性系数Kx为

(4)

(a)

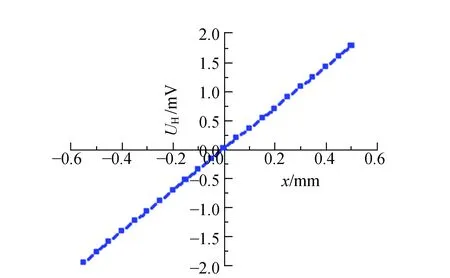
(b)图1 霍尔元件位移传感特性测量装置及霍尔电压随位移变化关系

3.2 实验装置设计

图2 所示为设计的实验装置，将霍尔元件固定到弹性模量测量仪的力学装置上，霍尔元件与金属丝(钢丝)的夹持部分(夹具)固定在一起，使两者能够同步运动. 均匀梯度磁场固定在夹具一侧，使得钢丝未拉伸时霍尔元件位于磁场中心. 钢丝上端固定，下端托盘上增加或减少砝码数量使得钢丝拉伸和还原,霍尔元件的位置会随钢丝拉伸而发生变化，霍尔元件的位移大小即为样品钢丝的伸长量δL.

图2 实验装置设计实物图

4 结果分析与讨论

4.1 金属丝几何参量测量

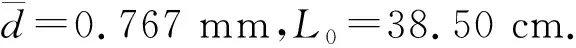
4.2 金属丝外加拉力时测量结果

钢丝竖直放置，在钢丝底部托盘内增减砝码，并记录霍尔元件产生的霍尔电压，测量数据如表1所示. 每增加1.000 kg砝码记录电压示数Ui(i=0,1，…，13)，再每减去1.000 kg砝码记录电压示数Ui#(i=0,1,…，13)，然后取其平均值作为第i次测量结果，以消除圆柱体和固定平台圆孔间的摩擦对测量结果的影响.

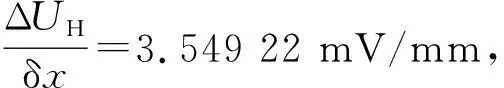
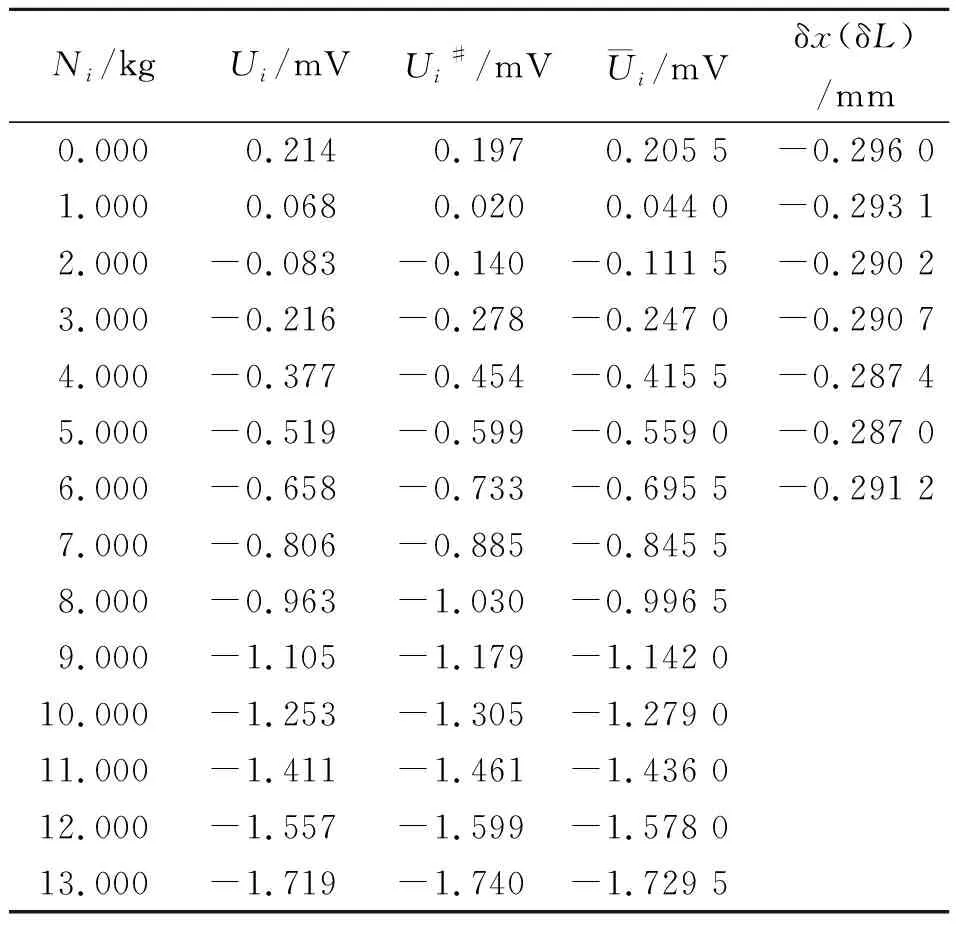
表1 增减砝码时数显电压表示数及对应位移

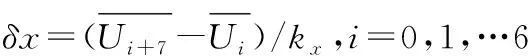
4.3 金属丝弹性模量的计算

(5)

以ΔUi为纵坐标，Ni为横坐标作图，如图3所示，曲线拟合为良好线性关系，斜率k=0.147 8 mV/kg. 因此，弹性模量E为

(6)

根据弹性模量的不确定度公式为

(7)

其中厂家提供Δm/m=0.6%；米尺测量ΔL0=0.5 cm；钢丝直径多次测量Sd2=1.228×10-4mm2，螺旋测微器误差Δ仪=0.004 mm，得Δd=0.012 mm；由表2得ΔδL=5×10-3mm，因此：

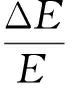
(8)

(9)

则金属丝弹性模量的最终测量结果为

(10)

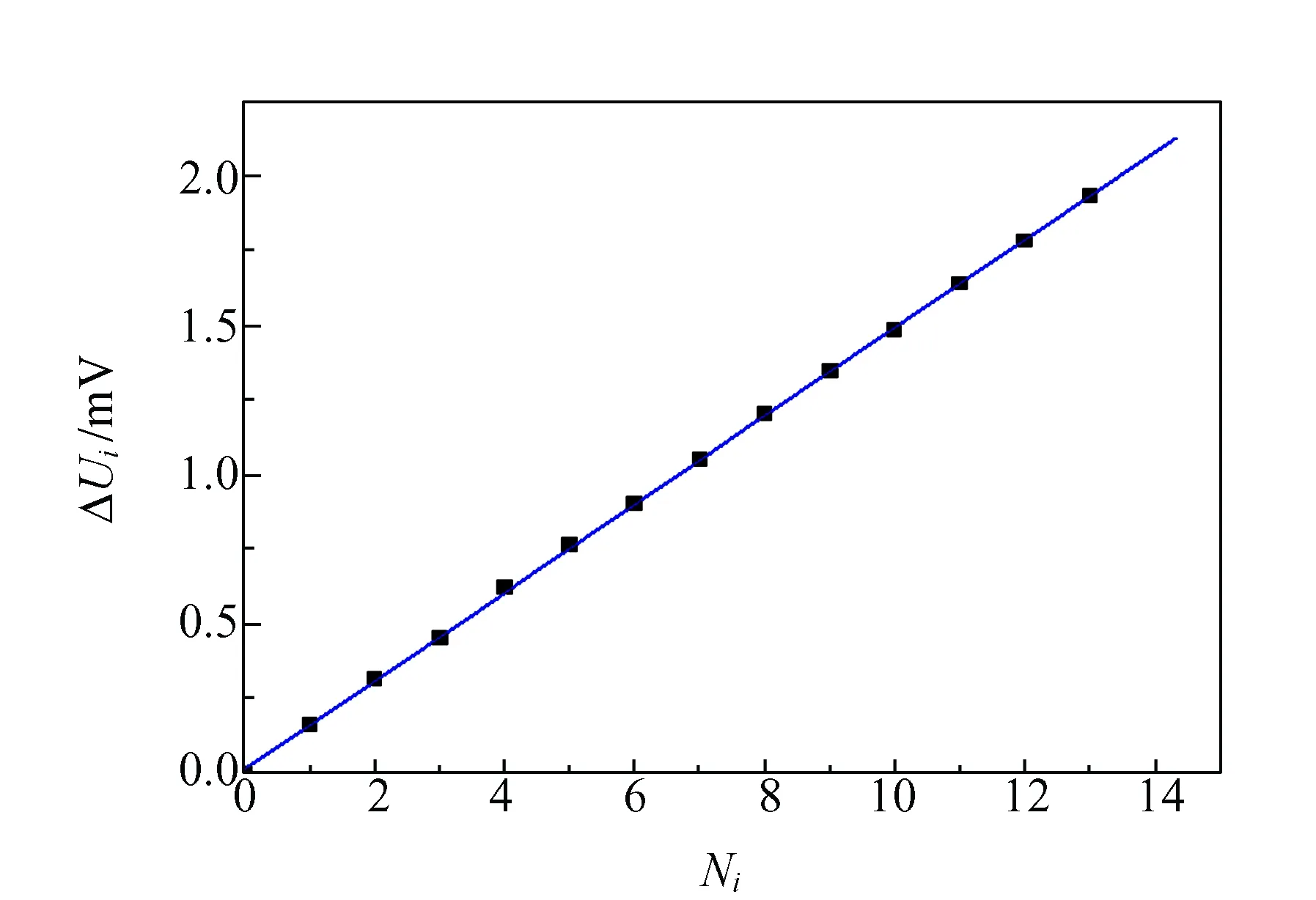
图3 霍尔电压随所加砝码变化曲线图

5 结束语

将霍尔元件应用于拉伸法测量弹性模量的实验中,替代光杠杆放大系统,通过测量霍尔电压得到微小位移. 结果表明，霍尔电压随位移变化为良好线性，采用作图拟合法计算求得金属丝的弹性模量，分析了实验结果的不确定度. 实验证明该测量方法测量精度高，准确性好，通过数字电压表测量霍尔电压巧妙地解决了微小位移难测的问题，提高了实验精度和实验效率；同时充实了大学物理实验教学内容，更可作为创新和研究型实验项目对学生开放.

参考文献：

[1] 邓金祥，刘国庆，原安娟，等. 大学物理实验[M]. 北京：北京工业大学出版社，2011:65-67.

[2] 刘芬芬，傅振国，朱茂健，等. 光杠杆放大法测量的误差分析及改进方法[J]. 大学物理实验,2013,26(4):92-95.

[3] 刘卓霖，杨一帆，陈苏，等. 基于霍尔传感器阵列的孔板流量计测流量实验[J]. 物理实验,2011,31(7):5-7.

[4] 蔡明，章英，白雪莲，等. 线性霍尔传感器技术及其在气动定位控制中的应用[J]. 仪表技术与传感器, 2013(1):13-15.

[5] 李东平，戴玉萍. 测定物体长度微小变化量的实验装置[J]. 物理实验,1996,16(2):72-74.

[6] 刘雪梅. 霍尔效应理论发展过程的研究[J]. 重庆文理学院学报(自然科学版),2011,30(2):41-44.