带有补偿器的结构弱抖振滑移模态控制研究

罗瑜，王社良，李志军,2，樊禹江

(1.西安建筑科技大学土木工程学院，西安710055；2.西安工业大学建筑工程学院，西安710032)

带有补偿器的结构弱抖振滑移模态控制研究

罗瑜1，王社良1，李志军1,2，樊禹江1

(1.西安建筑科技大学土木工程学院，西安710055；2.西安工业大学建筑工程学院，西安710032)

基于地震激励下固定阶次补偿器对线性结构的控制研究，提出一种利用复合趋近律的新型变结构主动控制算法。相对于传统变结构控制算法，该方法能够通过使用二次线性最优控制理论，均衡控制力和控制效果；并为有限输出反馈控制器在控制系统中的实际应用提供系统的设计方法。该方法能确保系统的稳定，保证抖振效应足够小。最后，对一个主动支撑系统的多自由度剪切型建筑模型进行数值模拟，验证先前的假设并证明这种新型控制方法的有效性。

振动与波；复合趋近律；变结构控制；抖振效应；补偿器；建筑结构

在土木工程领域，YAO于1972年首次提出结构振动控制这一概念，一个最常用的鲁棒控制计算方法是滑移模态法[1]。美国学者Yang率先将该方法引入结构控制中[2]。该方法反应迅速、对参数变化不敏感、抗干扰能力强等优点[3―6]。然而，由于传统滑模控制的抖振问题，实际的控制器应该得到能实现控制力的时程曲线[7]。因此，基于复合趋近律，本文提出一种新型的带有补偿器的滑移模态控制，它能减小地震响应。先前对滑模控制的研究中，控制力和控制效果的调制是通过改变切换面或者指定最大控制力（饱和控制器）。本文使用线性二次最优控制理论（LQR），引入固定阶次补偿器，提出了设计滑移模态控制器的方法[8]。

为减小建筑结构地震响应，现有的例如CAI et al[5]和ZHAO et al[6]的滑模控制方法，能避免过度的抖振效应[7]。本文用一个三层建筑模型的数值例子，证明这种控制方法的可行性。

1 结构体系的动力方程

对于一个自由度数为n的层间剪切型受控建筑结构，设地面运动的加速度分量为，其运动方程可表示为

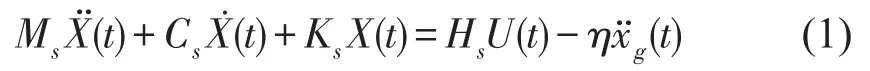
其中X=[x1，x2，…，xn]T为n维位移列向量（xi为第i层相对于地面的位移）；Ms=diag[m1，m2，…,mn]和η=[m1，m2，¼，mn]T分别为（n×n）维结构的质量矩阵和n维的质量列向量（mi为第i层的集中质量）；u（t）为r维控制力列向量；Hs为（n×r）维控制力位置矩阵和分别为（n×n）维结构阻尼和刚度矩阵。

将式（1）化为状态方程

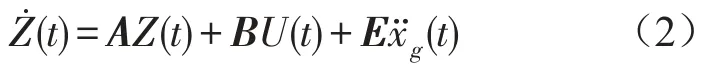
式中

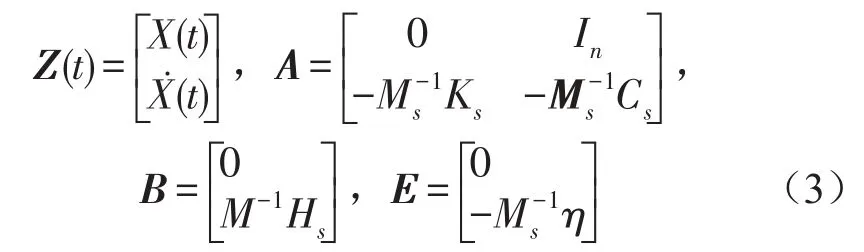
y维输出反馈向量可以表示为

2 带补偿器的滑移模态控制

滑模控制的设计应包含两步：切换面的设计和控制器的设计。

2.1 补偿器和切换面的设计

在滑模面的设计中引入一个固定阶次的补偿器，控制系统如图1所示。由于控制器的数量为r个，为简单起见，补偿器的阶数取为r+1，忽略外部激励的影响，则补偿器的状态方程如下

图1 结构控制系统框图

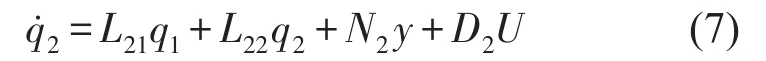
用补偿器的状态变量来构造理想切换面S=0[9]，即

式中S=[S1,S2,…,Sr]T为r维滑模面向量；P=[P1,P2]为r×（r+1）维矩阵为r列向量为r×r维矩阵。

由式（8）可得

这里假定P2是可逆的。在滑模面上，由[9],可得

式中

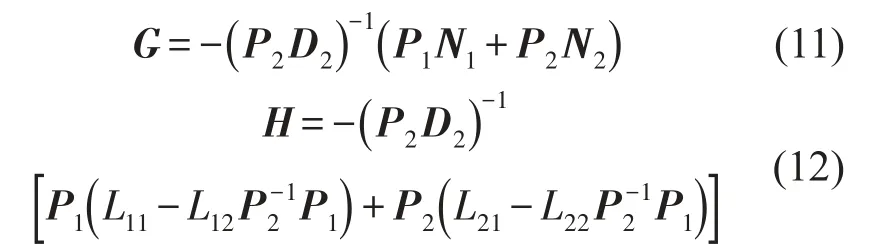
Ueq为使系统保持在滑模面上所需的控制力。

将式（10）代入式（2），可得在切换面上的闭环系统为

在切换面的设计中，忽略了外部激励的影响，而在控制律的设计中将考虑其影响。

将式（9）代入式（6），则可得由q1表达的补偿器在切换面上的运动方程

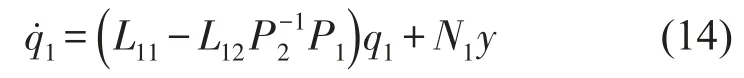
一旦q1确定后，则由式（9）可将q2确定，这样补偿器的状态向量就可确定。则由式（12）和式（13）可建立如下增广形式的结构—补偿器系统

式中

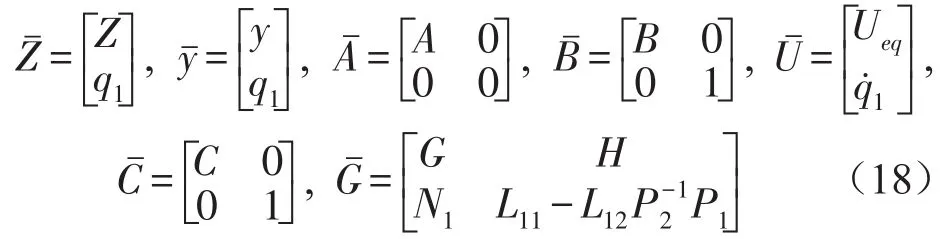
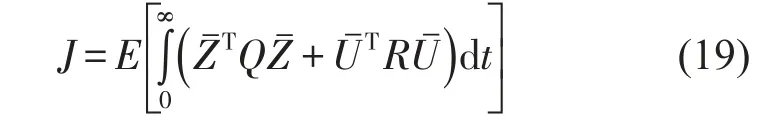
根据Levine和Athans[10]最优输出反馈控制理论，控制增益矩阵可通过解下列非线性矩阵方程得到

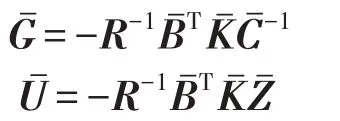
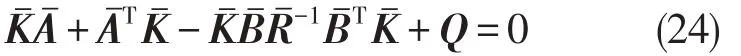
（1）G、H、N1和可由式（18）得到；

（2）G已知，选择非奇异矩阵P2、D2和任意的P1，则由式（11）可得N2；

（3）已知H，根据式（12），选择适当的L22可确定L21；

注意L12和L22选择的原则是要保证稳定，即要求的特征值均具有负实部。

2.2 控制器的设计

首先用高为炳[9]在90年代早期提出的指数趋近律

分析了上述指数趋近律的不利影响，考虑一个新型的复合趋近函数

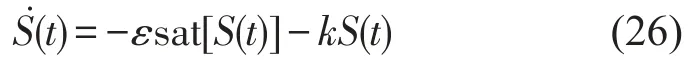
其中

补偿器所受的（r+1）维外部激励向量Ec(t)表示为

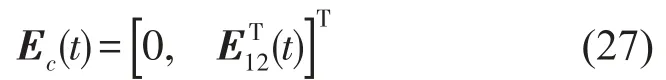
其中E12(t)是和控制力位置相对应的r维外部激励子向量。则式(7)可以重新表示为

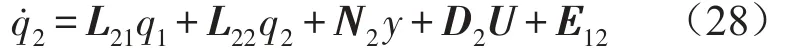
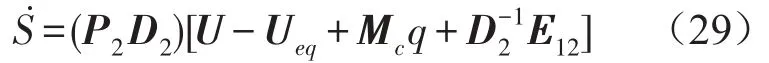
式中

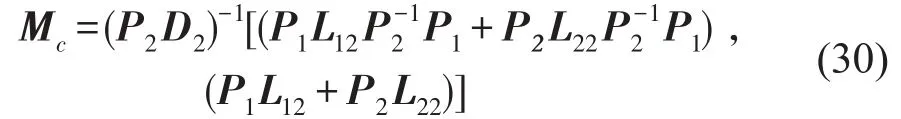
将式（30）代入式（26），可得控制力为

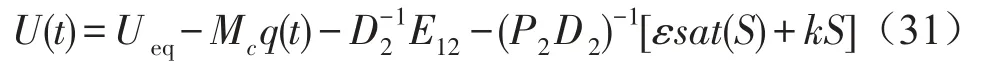
3 数值仿真研究

采用图2所示的结构模型进行数值分析，结构参数如下：结构各层集中质量为mi=1 000 kg；水平刚度为ki=980 Kn/m；阻尼系数为ci=1.407 kN·s/m (i=1-3)。输入采用EI Centro地震波，持续时间为8 s，最大地面运动加速度为[x¨g（t）]max=0.12 g；在结构第一层安装有主动支撑（ABS）作为作动器，式（26）中系数k取为10，Δ取0.05。

控制数确定如下：取

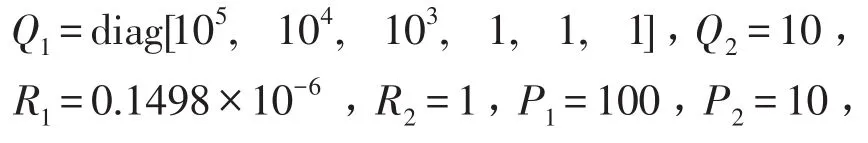
图2 结构模型

3.1 全状态反馈控制

当采用指数趋近律时，随着εi的不同取值，控制力的变化如图3所示。

从图3可以看出，随着ε值的增大，控制系统的抖振变得越明显，当εi的值较大时（εi=5.0），抖振已经很大，此时系统变得很不稳定。

然而，使用复合趋近律就可以避免过度的抖振。

表1中展示了结构未控和全状态反馈以及有限状态反馈时结构各层的最大位移、最大加速度，另外，用RD表示全状态反馈和有限状态反馈时结构位移和加速度相对于未控时的减少量。从表1观察发现，使用复合趋近律时最大控制力为5.10 kN。底层的最大层间位移和最大加速度（相对与地面）分别减少将近78%和34%；第二层相应减少了85%和35%；第三层相应减少了37%和44%。

带有补偿器的滑模控制以及未控时，底层全状态反馈的位移和绝对加速度时程曲线见图4所示。

从图中可以直观地看出，采用本章所提出的滑模控制方法能有效地减小结构的地震峰值响应。

图5是采用复合趋近律时结构控制力时程。可以看出，此时控制系统的抖振很小。

只在结构第一层安装有位移传感器和速度传感器。结构各层最大层间位移、最大加速度（相对于地面）和所对应的最大控制力如表1第8、10列所示。从表1可以看出，当采用复合趋近律的滑模控制方法时，控制效果也非常明显，但是与全状态反馈控制相比而言，其所需要的控制力较大，且控制效果稍差一些。

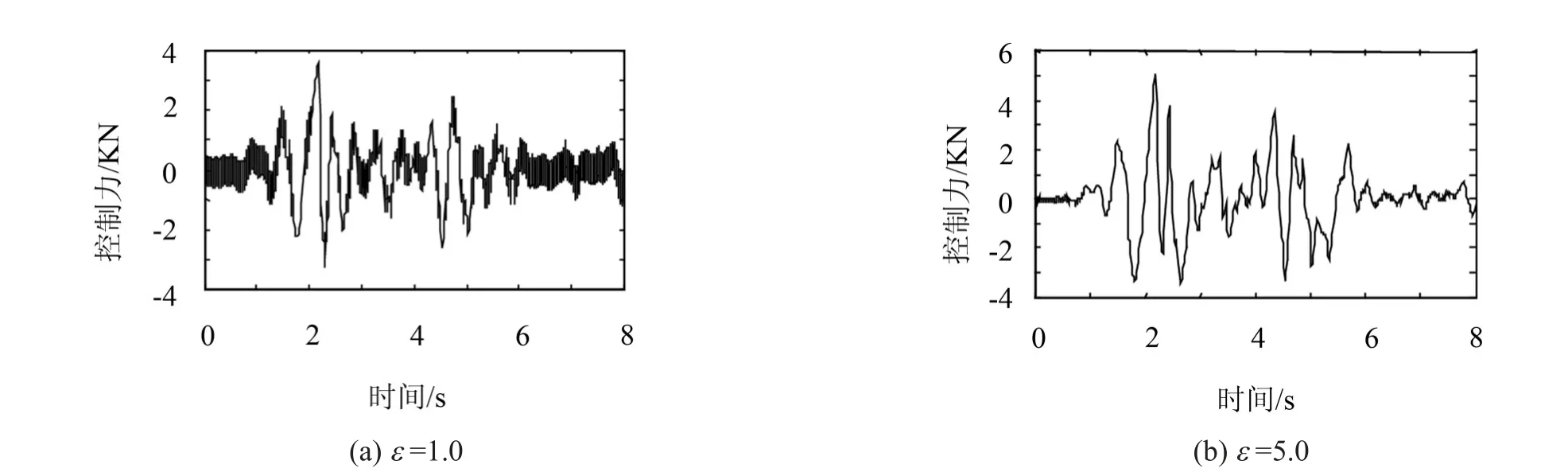
图3 采用指数趋近律时控制力的时程

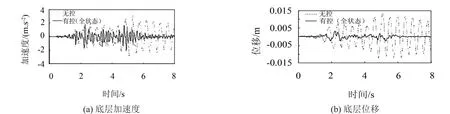
图4 底层地震反应时程（全状态反馈）

表1 结构地震最大反应和控制力

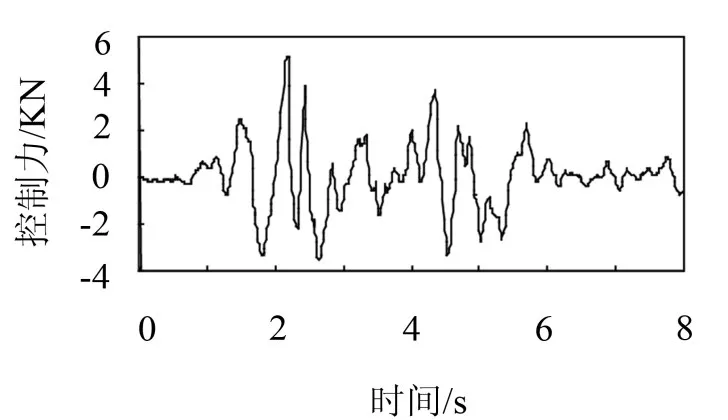
图5 基于全状态反馈的控制力时程（复合趋近律）

3.2 有限输出反馈控制

考虑有限输出反馈，假定除地面运动加速度外，结构底层加速度和位移反应时程如图6所示，从图中可以看出，控制效果也是比较明显的。

结构控制力时程如图7所示，从图中可以看出，控制系统的抖振很小。

图6 底层地震反应时程（有限状态反馈）

4 结语

基于饱和控制的优点，本文提出了带固定阶次补偿器的滑模控制器用于结构抵抗地震。相对于传统的滑模控制，其最大的优点如下：

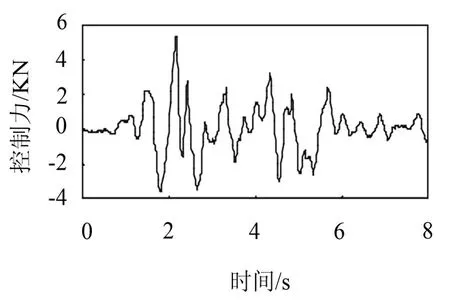
图7 基于有限状态反馈的控制力时程（复合趋近律）

（1）为均衡控制力和控制效果提供了简单的设计方法；

（2）能够利用有限的传感器，为静力输出反馈提供系统的设计方法；

（3）避免过度抖振。结果表明带有补偿器的滑模控制器能够应用于地震激励的结构中。

[1]盛严，王超，陈建斌，刘玉华.结构滑模控制的一种指数趋近律方法[J].噪声与振动控制，2004.04.

[2]YANG J N,WU J C and Agrawal A K.Sliding mode control for nonlinear and hysteretic structures[J].ASCE J.Engng.Mech.,Vol.121(12):1330-1339,1995.

[3]YANG J N,WU J C and Agrawal A K.Sliding mode control for seismically excited linear structures[J].Journal of Engineering Mechanics ASCE,Vol.121,No.12,pp: 1386-1390,December 1995.

[4]YANG J N,WU J C.Experimental verifications ofH∞and sliding-mode control for seismically excited buildings [J].Journal of Structural Engineering ASCE,Vol.122,No.1,pp:69-75,January 1996.

[5]CAI G P and HUANG J Z.Discrete-time variable structure control method for seismic-excited building structureswithtimedelayincontrol[J] Earthquake Engineering and Structural Dynamics,Vol.31,pp:1347-1359,2002.

[6]ZHAO B,LU X L and WU M Z.Sliding mode control of buildings with base-isolation hybrid protective system[J].Earthquake Engineering and Structural Dynamics,Vol.29, pp:3157-326,2000.

[7]Alli H and Yakut O.Fuzzy sliding-mode control of structures[J].Engineering Structures,Vol.27,pp:277-284,2005.

[8]Yang J N,et al.Sliding mode control with compensator for windandseismicresponsecontrol[J].Earthquake Engineering and Structural Dynamics,Vol.26,pp:1137-1156,1997.

[9]高为炳.变结构控制的理论和设计方法[M].北京：科学出版社，1996.

[10]Levine W S and Athans M.On the determination of the optimalconstantoutputfeedbackgainsforlinear multivariablesystems[J].IEEETrans.Automatic Control,Vol.15,pp:44-48,1970.

[11]Srinivasa Y G and Rajgopalan T.Algorithms for the computation of optimal output feedback gains[J].Proc.18th IEEE Conf.Decision and Control,pp:576-579, 1979.

Sliding Mode Control for Weak Chattering of Building Structures with Compensators Based on Hybrid Reaching Law

LUOYu1,WANG She-liang1,LI Zhi-jun1,2,FAN Yu-jiang1

(1.College of Civil Engineering,Xi’an University ofArchitecture and Technology, Xi’an 710055,China)
(2.School of Civil＆Architecture Engineering,Xi’an Technological University, Xi’an 710032,China)

A new active control algorithm based on the hybrid reaching law is proposed for the vibration control of linear structures with fixed-order compensators under seismic excitation.The main advantages of this method in comparison with the traditional variable structure control are as follows:(i)it can make a balance between control efforts and some special response quantities of the structure through the use of linear quadratic optimal control theory;(ii)it can provide a systematic approach for design of finite output feedback controllers to facilitate practical implementations of control systems;and(iii)the excessive chattering effect can be avoided by introducing the new method.Finally,numerical simulation for a multi-DOF shear-type building model containing an active brace system is given.The simulation results show that the new control algorithm is quite effective.

vibration and wave;hybrid reaching law;variable structure control;chattering effect;compensator; building structure

TU352.1

ADOI编码：10.3969/j.issn.1006-1335.2014.02.009

1006-1355(2014)02-0041-05

2013-07-19

陕西省工业攻关项目(2013K0707)；陕西省教育厅自然专项(2013JK0612)；西安工业大学校长基金重点项目(XAGDXJJ0919)；国家自然科学基金（51178388、51008245）；陕西省教育厅重点重点实验室科研计划项目（11JS059、12JS055）；陕西省重点实验室访问学者项目（12JS055）。

罗瑜（1989-），女，陕西西安人，在读硕士研究生，目前从事振动控制在土木工程中的应用方面的研究；

王社良（1957-），男，陕西西安人，博士生导师，目前从事结构智能控制及防灾减灾方面的研究。

E-mail:annal-y@hotmail.com