N=2的Neveu-Schwarz超共型代数的结构

付佳媛，邵霞，谭晓

(中国传媒大学 理工学部，北京100024)

1 前言

大概三十年前超共型代数由数学家Kac和物理学家Ademolloetal分别同时构造得到的。作为Virasoro代数的推广，此类代数的结构和表示理论将对其他代数，尤其是李超代数的研究有重要的推动作用。在数学方面，Kac和vandeLeuer[5]，Cheng和Kac[2]已经给出了超共型代数的所有可能的分类，而后Kac又证明了这些分类是完全的。

结构和表示理论同样是超共型代数的两个重要研究方向。对于超共型代数的研究，目前只有N=1的情况得到了比较完整的结果，对于N=2的情况我们知之甚少。目前已知三类N=2的超共型代数：Romand超共型代数，Neveu-Schwarz超共型代数和Topological超共型代数。对于N=2的Romand超共型代数，文献[3]中已经对其结构进行了详细讨论，并给出其中间序列模的完整分类。本文我们将对N=2的Neveu-Schwarz超共型代数的结构进行讨论。有了对此类代数结构的详细刻画，我们才能对其表示进行深入的讨论。

2 预备知识

由于超共型代数与李代数的密切关系，我们先给出几类李代数的定义。本文中我们用F，C，Z分别表示特征零的代数闭域，复数集，整数集。

定义1 我们称一个李代数Vir=spanF{Li，c| i∈} 为Virasoro代数，其中c∈ C为中心元素，如果基元素Li，c满足如下Virasoro关系式：

定义2 我们称一个李代数L=spanF{Li，Hj，c|i，j∈}为扭的Heisenberg-Virasoro代数，其中c∈ C为中心元素，如果基元素Li满足Virasoro关系式，且有满足如下关系式：

[Li，Ij]=-jIi+j-δi+j，0(i2+i)c，[Hi，Hj]=iδi+j，0c

我们称一个Virasoro代数的模M为Harish-Chandra模，如果M具有有限维权空间分解，即

M=⊕λ∈CMλ，dimMλ<∞

这里Mλ={x∈M|L0x=λx}。

关于Virasoro代数的Harish-Chandra模我们有如下结论[7]：

定理1 如果M=⊕λ∈CMλ是Virasoro代数的不可约Harish-Chandra模，则M一定是(1)最高权模，(2)最低权模或(3)中间序列模。这里中间序列模是指dimMλ≤1，∀λ∈C。

定理2 Virasoro代数的中间序列模只能是Aa，b，A(a)，B(a)，a，b∈ C或者是其商模，并且Virasoro代数的中心元素c在模上的作用为零。这里模Aa，b，A(a)，B(a)都具有基元素{xk|k∈}，且满足：

A(a，b)：Lixk=(a+k+bi)xi+k，

A(a)：Lixk=(i+k)xi+k，k≠0，Lix0=i(i+a)xi，

B(a)：Lixk=kxi+k，k≠-i，Lix-i=-i(i+a)x0

定义3 N=2的Neveu-Schwarz超共型代数

3 无中心元素的低维表示

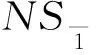
[Lm，Gr]=(a-r+mb)Gm+r，[Hn，Gr]=fGn+r，

其中a，b，f∈ C，f=0。设

[Gr，Gs]=arsLr+s+brsHr+s

利用Jacobi等式：

[Hk，[Gr，Gs]]=[[Hk，Gr]，Gs]+[Gr，[Hk，Gs]]，

令k=0，可得2f[Gr，Gs]=0，故

[Gr，Gs]=0，∀r，s∈

[Li，Lj]=(i-j)Li+j，[Hi，Hj]=0，[Li，Hj]=-jHi+j

其中a+，a-，b+，b-，f1，f2∈C，r∈且(f1，f2)≠(0，0)。接下来我们将确定如上关系式中的常数。由Jacobi等式

可得a+=a-。记a+=a，令

由Jacobi等式

取k=0，可得a=0。取k=0，

左边=ars(k-r-s)Lk+r+s+brs(-r-s)Hk+r+s，

右边=((-r+kb-)ar+k，s+(-s+kb+)ar，s+k)Lr+s+k

+((-r+kb-)br+k，s+(-s+kb+)br，s+k)Hr+s+k

左边=右边，因此有

(3.1)

于是

brs+bks=ars(-k+(r+s)b-)+aks(-r+(k+s)b-)

令k=r，可得

brs=ars(-r+(r+s)b-)

(3.2)

brs=-ars(-s+(r+s)b+)

(3.3)

由(3.2)和(3.3)可得

b++b-=1

由

可得

其中k∈，r，s∈令可得

(3.4)

(3.5)

brs=d(-r+(r+s)b-)

4 中心扩张

[Li，Lj]=(i-j)Li+j；

[Hi，Hj]=0；

[Li，Hj]=-jHi+j；

这里b++b-=1。在这一节里我们将考虑此代数的中心扩张。

考虑李超代数的中心扩张，自然要定义一个2-上圈。所谓2-上圈是指：设ɡ是域F上的李超代数，ɡ上的双线性函数ψ，如果满足：

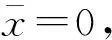
f(H0)=φ(L1，H-1)

(4.1)

ψ=φ-φf

其中

φf(x，y)=f([x，y])，

则我们可以得到如下一些等式：

其中i≠0，

=0，∀j∈

ψ(L0，H0)=ψ(L0，[L1，H-1])

=ψ([L0，L1]，H-1)+ψ(L1，[L0，H-1])

=-ψ(L1，H-1)+ψ(L1，H-1)

=0，

2ψ(L0，H0)=ψ(L0，[L1，L-1])

=ψ([L0，L1]，L-1)+ψ(L1，[L0，L-1])

=-ψ(L1，L-1)+ψ(L1，L-1)

=0，

接下来我们来确定各中心元素的值。

4.1 导出中心元素cL

根据前面确定的代数结构，我们有

ψ(L1，L-1)=φ(L1，L-1) -φf(L1，L-1)=φ(L1，L-1)-2f(L0)=0

从而

(i-2)ψ(Li，L-i)=ψ([Li-1，L1]，L-i)

=ψ(Li-1，[L1，L-i])-ψ(L1，[Li-1，L-i])

=(i+1)ψ(Li-1，L-i+1)-(2i-1)ψ(L1，L-1)

=(i+1)ψ(Li-1，L-i+1)

设ψ(Li，L-i)=li，可以得到

则对于∀i≥3

令l2=cL∈ C，所以有

4.2 导出中心元素cH

由于ψ(H0，H0)=ψ([H1，L-1]，H0)=ψ(H1，[L-1，H0])-ψ(L-1，[H1，H0])=0，我们设ψ(Hi，H-i)=hi，i≠0，那么

(i-1)hi=(i-1)ψ(Hi，H-i)

=ψ([Hi-1，L1]，H-i)

=ψ(Hi-1，[L1，H-i])-ψ(L1，[Hi-1，H-i])

=iψ(Hi-1，H-i+1)

=ihi-1

因此有hi=ih1。若令h1=cHC，则有ψ(Hi，H-i)=icH，∀i∈成立。

4.3 导出中心元素cHL

首先我们要来考虑ψ(Li，Hi)的关系：

ψ(L1，H-1)=φ(L1，H-1) -φf(L1，H-1)

=φ(L1，H-1) -f(H0)

=0，

那么有

-(i-1)ψ(L-i，Hi)=ψ(L-i，[L1，Hi-1])

=ψ(L1，[L-i，Hi-1])+ψ([L-i，L1]，Hi-1)

=-(i+1)ψ(L-(i-1)，Hi-1)，

从而(i-2)ci=ici-1。设ψ(Li，H-i)=ci∈ C，则有

又令c2=cHL，得：

4.4 导出中心元素cG

由式(4.1)知，

那么

即得

因此

即

因此

至此我们推导得出所有N=2的Neveu-Schwarz的超共型代数的中心元素。实际上，由Jacobi等式，我们可以确定各个中心元素之间的关系，从而简化李超运算的形式。

1.cHL和cH之间的关系

同理可得

cHL=(1-2b)cH

2.cG和cH，cL和cH之间的关系

根据Jacobi等式，

其中i∈，r，s∈我们可以得到

上式两端用ψ作用，且假设i+r+s=0，可得：

(4.2)

(4.3)

将(4.3)代入可得

cL=(-10b2+14b-3)cH

通过上面所求出来的公式和定义我们可以得到一个含有中心元素的超代数

满足如下关系：

[Hi，Hj]=icHδi+j，0；

[Li，Hj]=-jHi+j；

[1]孟道骥.复半单李代数引论[M].北京：北京大学出版社，1995.

[2]S L Cheng，V Gkac.A new N=6 superconformal algebra[J].Comm Math Phys，186，219-231.

[3]Jiayuan Fu，Cuipo Jiang，Yucai Su.Classification of modules of the intermediate series over Ramnond N=2 superconformal algebras[J].Anhui 4230026，2004.

[4]B GatoRivera，J I Rosado.Families of singular and subsingular vectors of the topolgical N=2 superconformal algebra[J].Nucl Phys B514，477-522，1998.

[5]V Gkac，vandeLeuer. On Classification of Superconformal Algebras：Strings 88[J].Sinapore，WorldScientic，1988.

[6]C Martin，A Piard.Indecomposable modules for the Virasoro Lie algebra and a conjecture of Kac[J].Comm Math Phys 137，109-132，1991.

[7]Y Su.Classification of Harish-Chandra Modules over the Super-Virasoro Algebras[J].Comm Ale 23(10)：3653-3675，1995.