基于数据挖掘技术的大学生选课系统应用研究

张潇月，李波

(中国传媒大学 理学院，北京100024)

1 引言

“啤酒与尿布”的故事可以说是营销界的经典段子。沃尔玛发现，在超市购物中这种某些特定物品往往存在平时不易察觉的联系，尝试顺应这种联系调整超市格局，从而获得了很好的商品销售收入。如今，“啤酒与尿布”的故事在更多的领域得到了应用。

在目前中国大学里，选修课制度普遍存在。但据实情而言，中国大学的公共选修课开展情况与发达国家大学相比远有不足之处。究其原因除了中国大学生人数比国外多之外，更大的原因是国内很多大学选课制度不够合理，选课系统不够完善。每年选课期间往往会出现选课系统崩溃、网络服务器超负荷运作等现象，使学生选不到自己想上的课，课程不能分配给需求最为迫切的学生，造成了大量教学资源的浪费。

从某种角度说，大学生选课和顾客挑选商品有异曲同工之妙。顾客需要在最短时间内买到自己需要的商品，大学生也需要在最短时间内选到最适合自己的选修课。如果能为这种需求从数据上提供科学的解决方案，学校就能完善选修课系统，使学生选课过程更加科学快捷，从根本上解决了大学生选课难的问题。本文利用关联规则算法，对大学生选课的数据进行处理和深度挖掘，并从中分析出课程之间存在的联系，从而给出对大学生选课系统改进的合理化建议。

2 数据预处理及图形化

本文采用的数据来源于数据堂网站《中国科技大学学生选课数据2013.10.03》(http://www.datatang.com/data/45084)。将数据导入clementine软件中，得到中国科技大学学生选课数据。该数据库一共使用了2678个有效样本，并对该学期开设的44门公选课选修情况进行了罗列。C1、C2、C3…C44分别代表该学校开设的44门公选课。将数据进行清洗和处理，处理过程此处省略，处理所得数据见表1。

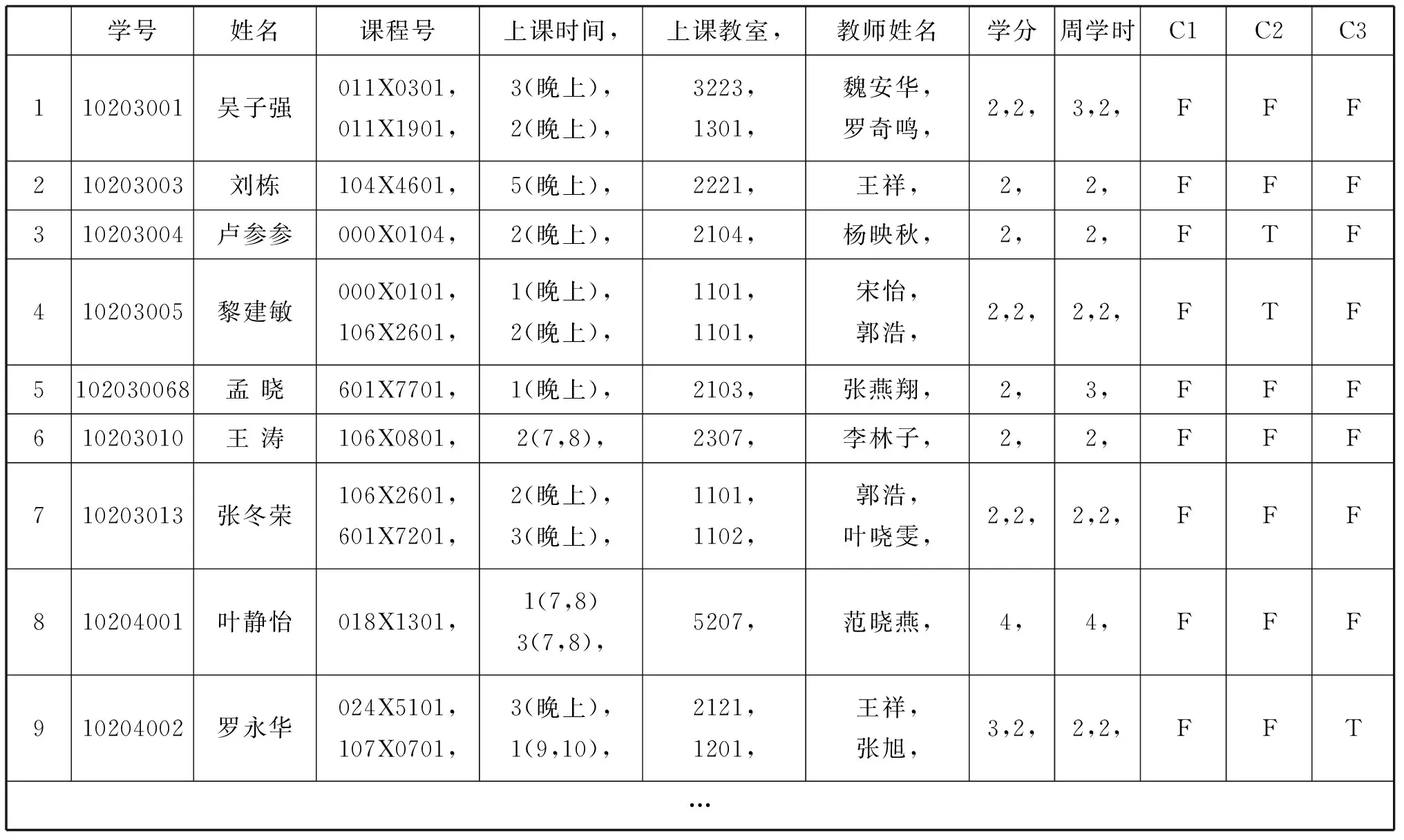
表1 学生选课对照表(部分)

为了发现课程之间的内在联系，本文主要使用的方法是关联分析。关联分析又称关联挖掘，就是在交易数据、关系数据或其他信息载体中，查找存在于项目集合或对象集合之间的频繁模式、关联、相关性或因果结构。或者说，关联分析是发现交易数据库中不同商品(项)之间的联系。数据挖掘的目的是为了发现各门课程之间的关联，因此一些无关紧要的信息就是没有用的，所以把姓名、课程号、上课时间、上课教室、教师姓名、学分、周学时这几个字段剔除。

关联分析的目的是看出课程之间存在的联系。由于直接从表格中很难看出各门课程之间的联系，我们首先使用“网络”图形分析模型对数据进行初步直观的观察。“网络”图形来分析结果如图1所示，该图表示的是所有课程之间的联系，每一个节点表示一门课程，课程之间的连线表示存在的联系。线条越粗表示课程之间的关联程度越强。

图1 各课程间联系的“网络”图

首先，可以调节显示比例，把弱的关联规则从图中去掉，最终保留相关性最强的几门课程，重点分析其内在联系。图1中显示C29(黑客反向工程技术)和C35(社交舞蹈(女步))之间的关系是最强的。这一结果出乎很多人的意料，这两门看似毫不相关的课程却有着最强的联系。这说明，很多学生会同时选择这两门课程，因此当选课系统检测到学生选取了其中一门课程的时候，就可以在页面上出现另一门课程的快捷选课链接，对学生进行推荐，这样就大大节约了选课的时间。

进一步的观察还可以从图中明显地看出，C41(中国古史大观)和C44(综合技能培训)这两门课程与其他课程之间的联系较少，尤其是C41只与一门课程之间存在较强的关联规则，这可能与课程本身在学生中的受欢迎程度有关。因此这门课程在新的选课系统中不容易被推荐到，需要被放在比较明显的页面上，以保证其课程容量。而连线越多越粗的课程，则说明与很多课程之间都存在较强联系，容易在各个组合中都被推荐选课，因此不必放在首页上，节省出学生选课时重复浏览相同信息所浪费的时间。

为了用量化的方法更科学地分析这种关系，下面我们用关联规则来分析。

3 大学生选课系统的关联规则建模及算法

3.1 大学生选课系统的GRI算法

GRI是关联规则的一种算法，其表示的规则形式是：If Y=y then X=x with probability p，其中X和Y是两个指标，x和y是两个指标的值，then前面的是条件，后面的是结果。符合条件的规则将按一定顺序选入规则集表中。下面简单介绍此项研究中GRI算法的思路。

GRI算法的基本思路是依照深度优先搜索策略进行分析的。从后项入手，逐个分析后项，分析完一个后项再分析下一个后项；在分析每个后项的过程中，逐个分析前项所包含的具体类别(项目)，分析完一个类别后再分析下一个类别；在分析每个类别的过程中，逐个分析前项，分析完一个前项再分析下一个前项；在分析每个前项的过程中，逐个分析前项所包含的具体类别(项目)，分析完一个类别后再分析下一个类别，所以是一个深度优先策略。

设：有m个后项，记为Y；第i个后项Yi有C(Yi)个类别。由于Clementine中的GRI算法只能处理事实表数据，后项只有1和0两个取值，因此C(Yi)都为2。

有n个前项，记为X，第k个前项记为Xk，第k个前项Xk有C(Xk)个类别，同理，Clementine中C(Xk)都为2。

该过程用程序表示如图2所示。

下面介绍一下计算值的方法，这也是整个算法的关键。

在本文中，前项为待选的44门课程，后项为是否选择该课程，依据样本统计结果可得2表所示。

其中p(x)为选了课程C1的概率；p(y)为选了课程Y的概率，为先验概率；p(y|x)为选了C1课程的同学选择Y课程的概率，为条件概率。于是J-值定义为：

J(y|x)=p(x)[p(y|x)+(1-p(y|x)) ]

可见，J-值反映的是选择了C1这门课程的同学同时选择Y课程和不考虑有没有选C1课程的同学选择Y课程的先验概率分布的差异，并经p(x)调整后的结果。这个差异越大，就说明两门课程之间的联系越紧密，选择J-值最大时的课程组合，这些组合的课程之间的影响作用是最明显的，由此生成的关联规则才是有效的。

For i=1to m //循环m个后项For j=1 to C(Yi) //循环第i个后项的C(Yi)个类别For k=1 to n //循环第i个后项Yi的的第j个类别的n个前项//对第i个后项Yi的第j个类别的第k个前项Xk进行处理,确定类别数SIf Xk 类型=分类型 Then S=C(Xk) End If //Xk为分类型则分为C(Xk)组If Xk 类型=数值型 Then S=2 End If //Xk为数值类型则分为两组For l =1 to S //循环第i个后项Yi的第j个类别的第k个前项Xk的S个类别计算Xk为第L个类别时的J-值If J-值大于相同输出下的J-值的最大值,或规则数目小于指定生成的规则数且支持度和置信度均大于阈值Then生成一条推理规则End IfEnd ForEnd ForEnd ForEnd For

图2 GRI算法的程序表示

同理，计算其它43门课程的J-值，就可以找出存在内在联系的课程，得出相应的关联规则。

在Clementine 软件中GRI模型的流程图如图3所示。

在clementine中添加GRI模型节点。执行后得到结果如表3所示。

从计算结果可以清楚的看出来，C10(桥牌基础讲座与技巧)、C39(现代日本语言与文化(初级))以及C29(黑客反向工程技术)之间存在较强的相关联系。同样的，如果系统检测到有同学如果选修了前两门课程时，系统就可以自动在页面上为其推荐选修第三门课的快捷链接，大大加快了选课的效率，减轻了系统的负担。诸如此类的课程组合还有很多，比如C38(西方油画艺术赏析)、C39(现代日本语言与文化(初级))、C11(色彩); C26(电子信息检索)、C42(中国文化史)、C11(色彩)等。

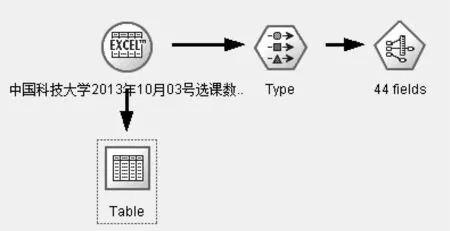
图3 GRI模型算法流程图

后 项前 项支持度%置信度%C29C10 C390.04100.0C11C38 C390.04100.0C11C26 C420.04100.0C25C22 C430.04100.0C26C11 C420.04100.0

从表面上看，这些选修课之间并无太大联系，这与选修课本身的特性有关。大学生选修课大多是为了在学习本专业课程之余，为学生提供其他领域的学习机会，因此涉及的范围非常广泛。同时学生也会根据自己的兴趣爱好，选择不同类型的课程，很少有学生同时选择两门十分相似的选修课，比如C41(中国古史大观)和C42(中国文化史)，在此次研究的样本中，这种组合几乎是不存在的。这也就是传统的选课系统往往把同种类型的课程放在一起，导致选课效率大大降低的原因。GRI模型的意义就在于找出所有课程中，学生最喜欢的课程组合，当同种情况出现时，将学生最有可能感兴趣的课程推荐给他，从而达到快速选课的目的。

3.2 利用决策树模型挖掘学生心理问题的信息

在关联分析中，决策树(Decision Tree)是一个预测模型，是数据挖掘分类算法的一个重要方法。在各种分类算法中，决策树是最直观的一种。他代表的是对象属性与对象值之间的一种映射关系。可以将分析对象的各种情况分类、组合，并且形象直观的表示出其关系及组合发生的概率，从而进行预测。

之前的研究中只考虑了各门课程之间的关联规则，没有考虑到学生的个人信息。其实学校的教务在线系统往往能掌握以往学生全面的资料。根据这些资料，可以挖掘出很多有用的信息，并对后来的学生进行选课的指导和帮助。接下来，将以挖掘学生心理问题为例，探讨决策树模型在学生选课系统中的应用。

由于是否存在心理问题属于学生个人隐私，网上无法查找到相关的数据。在这里我根据存在心理问题的学生在全部大学生中所占的比例(约为20%)，进行系统抽样，将抽出的学生标记为存在心理问题的学生，以此模拟出模型所需要的数据库。学校在实际的操作中，可以通过问卷调查、心理咨询、一对一谈话等方式了解学生的心理状况，得到科学合理的数据，从而计算出更加准确有效的模型。

假设我们把选择了艺术性较强的课程的学生称为“偏好艺术型学生”，那么在偏好艺术型学生中，满足哪些条件的学生很可能具有心理问题，需要对其进行特殊的选课照顾和指导呢？

决策树模型的输出结果包括树形图和规则集，模型正确率都达到80%以上，说明该模型在这项研究中是科学合理的，之后将对各个步骤进行详细说明。

得到了新的数据后，再次插入类型节点，选择需要进行数据挖掘的字段，这里主要包括：该学生是否存在心理问题、上课时间、学分这三个字段。之后，添加决策树模型节点，设置剪枝程度为85%，导出树形图,部分树形图如图4所示。

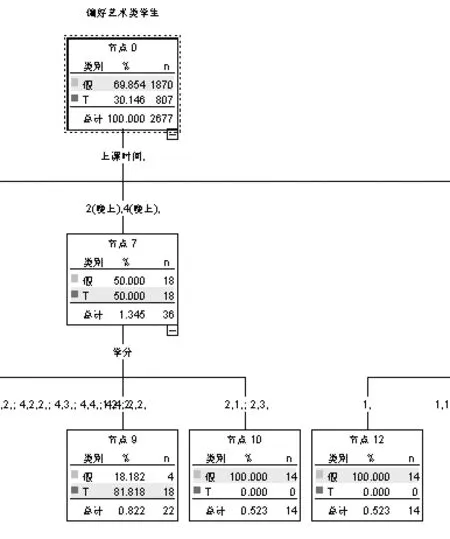
图4 决策树模型结果图

以截取的这部分树形图为例进行观察分析，可以得出结论：以往的学生数据显示，在“偏好艺术型学生”中，大约有百分之三十的学生有心理问题，根据其上课时间进一步细分，在周二晚上和周四晚上选了艺术类课程的学生，有心理问题的人达到了一半。而其中，选择学分较低的(1,2)、(2,2)这种组合课程的学生，有心理问题的概率几乎达到了百分八十左右。

这一信息在选课系统的设计中是很有用的。当系统检测到某些学生的选课迹象满足这些条件，表明这一学生很有可能是潜在的心理问题学生，因此系统可以适当的为其推荐一些能够锻炼身体、调节心情并能够促进该学生和老师及其它同学沟通交流的课程。比如瑜伽、健身、定向越野、音乐赏析等课程。这里由于使用了模拟的数据库，得到的结论不一定准确。但在实际的数据库中，这种特征可能会更加明显，并且随着样本量的增大，模型的拟合度也会更高。

分析该模型准确度，得到结果如表4所示。模型的准确度达到了82.29%，说明即使修剪程度达到85%，该决策树还是包括了大部分数据库中的信息，并且使数据得到了大大的简化，其优越性是显而易见的。

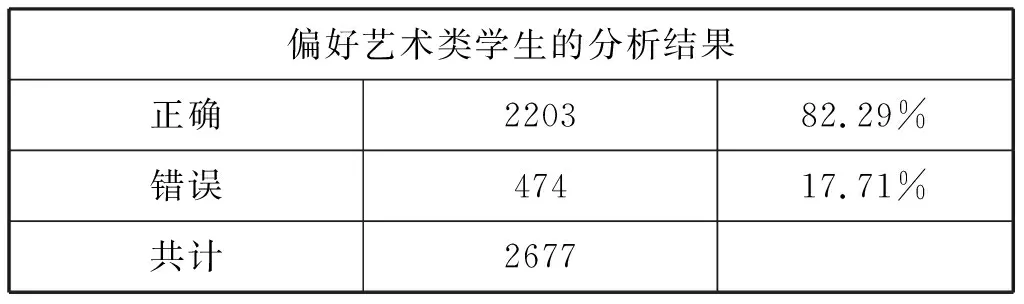
表4 决策树模型准确度分析

4 研究总结

本文主要研究clementine购物篮数据挖掘技术在大学生选课系统中的应用，使用的的几种方法都是有效且具有实际应用价值的。GRI模型和“网络”图形模型具有广泛的应用前景，决策树模型是数据挖掘中一种最常用的技术，它可以用于分析数据，也可以用来作预测。

本文主要利用Apriori模型、GRI模型和“网络”图形模型分析出各门选修课程之间的关联规则，并给出了改进选课系统的方案，为提高选课效率给出了科学的指导建议。另外，利用决策树和规则集模型，通过选修的课程对学生的个人信息进行挖掘，从而帮助学校更加准确地掌握学生信息，对其进行选课的指导和帮助。

实际生活中大学生选课所面临的问题要复杂很多，学校在管理制度和设计选课系统的时候，如果能得到大量数据的支持，用此类科学的方法解决选课难的核心问题，想必对整个学校乃至国家的教育资源合理化分配都是很有用的。

[1]刘同明.数据挖掘技术及其应用[M].北京：国防工业出版社，2001.

[2]Jiawei Han，Micheline Kamber.数据挖掘概念与技术[M].北京：机械工业出版社，2001.

[3]SPSSFORWINDOWS简明教程目录[J/OL].httP:www.fjmu.edu.cn/news/sPss/doe3/index.

[4]刘勤，金王焕.分类数据的统计分析及SAS编程[M].北京：复旦大学出版社，2002.

[5]Feng Tao，Fionn Murtagh，Mohsen Farid.Weighted Assoeiation Rule Mining Using Weighted Support and Significance Framework[J].Inproe 2003ACM SIGKDD Int Conf on knowledge discovery and data mining，2003.

[6]元昌安.数据挖掘原理与SPSS Clementine应用宝典[M].北京：电子工业出版社.

[7]张文献，陆建江.加权布尔型关联规则的研究[J].计算机工程，2003，29(9):55-57.

[8]周洪旭，谭秀梅，王峰.关于对大学生选修课问题的调查研究[J].莱阳农学院学报(社会科学版)，2004，16(4).