基于排队论模型分析生化恐怖袭击事件的医疗救助能力

王斌，王菊韵

(中国传媒大学 理工学部，北京 100024)

1 前言

生化恐怖袭击一旦发生对社会和人民生命会带来极大的威胁，如已发生的日本地铁沙林毒气事件和美国炭疽事件。1994年6月27日，松本市遭受了沙林毒气的袭击，事件造成7人死亡。二年后的1995年3月20日，沙林毒气袭击事件在东京地铁站再次发生，事件造成12人死亡，6000多人受伤。当这样的恐怖袭击发生后，受害者的自救能力和医疗救助方式与其他的灾害并不相同[1][2]。因此，在生化恐怖袭击发生时，分析和预测医院的救助能力，使受害者的伤亡减少到最低，是事故救援中的最重要的问题。

文中主要研究两个问题：(1)当生化恐怖袭击发生时，分析计算受害人群到达首选医院的人数。(2)在救助黄金时间，受害者首选医院的救助能力及受害者等待时间的计算。

2 方案和研究目的

基于上文中提到的日本沙林毒气事件，我们设置如下的研究场景。在一定时间里，北京某地铁站里有上百人(包括等地铁的和换乘地铁的人群)。刺激性气味从可疑物体发出后，迅速蔓延到整个站台。许多人已经有了中毒现象，开始恶心、流泪，一些靠近可疑物体的人有了更严重的症状。此时，乘客开始冲出地铁站寻找最近的医院寻求治疗，并且许多伤者进入的都是离地铁站最近的医院。

如果等待时间超过了黄金时间，可能会影响受害者的治疗甚至造成伤亡人数的增加。所以，根据医院的救助水平，受害者人数等，需要计算出平均救助时间和相关的参数。这些参数可以表示出医院的医疗救助能力。

3 计算到达率模型

3.1 瞬态系统中计算到达的受害者人数

传统方法中，排队论是对时间间隔相对较长下顾客到达情况的理论研究。即顾客的到达时间服从泊松分布并且到达时间间隔和服务时间服从指数分布。经一段时间后该系统会达到稳态的排队系统。

生化恐怖袭击的特征是发生概率低和有很大的不确定性。并且在短时间内会聚集大量受害人群，所以，当恐怖袭击发生时，预测受害人群涌入医院的情况不能用传统的排队论系统。当人们心理恐慌时，大量受害人会在短时间内涌入医院，因此顾客到达是非稳态的，基于这种情况我们需要建立一个瞬态行为系统，从而估计每个时刻到达医院的受害者人数，以及对到医院的受害人数作出判断，预测在“黄金救助时间”内医院的救治能力。

假定在时刻t受害者到达医院，到达时间服从近似泊松分布，到达率为λ(t)。医院有s(t)个并行服务台，服务时间服从指数分布，服务率为μ(t)。医院能容纳的受害者人数最多为N。

设pi(t)表示系统在初始状态下，在时间t时系统中有i个受害者的概率。p0(0)=1，如果i>0，pi(0)=0。通过下述模型，计算出在t+△t时刻系统中有i个受害者的概率：

P0(t+△t)=(1-λ(t)△t)P0(t)

+μ(t)△tPi(t)

(1)

Pi(t+△t)=λ(t)△tPi-1(t)+(1-λ(t)△t

-min(s(t)，i)μ△t)Pi(t)

+min(s(t)，i+1)

μ(t)△tPi+1(t)

(2)

1≤i≤N-1

PN(t+△t)=λ(t)△tPN-1(t)

+(1-min(s(t)，N)μ(t)△t)

PN(t)

(3)

上面的等式可以计算在时刻t+△t时，到达或者接受服务的受害者的概率。E(t)表示在某时刻等候和接受治疗的人数，它的平均值如下表述：

(4)

3.2 医院医疗救助能力的计算

当受害者的平均到达率λ小于医院的平均服务率μ时，可用传统排队论计算受害者等待时间，本文主要讨论受害者的平均到达率λ大于医院的平均服务率μ的情况。

当λ>μ时，医院没有足够的救助能力。这时系统是有限的，医院救助能力可以通过排队论模型 (M/M/S/GD/c/∞)计算。这个系统中，到达时间间隔和服务时间都服从指数分布，每个受害者接受服务的时间是独立的，并行服务台个数(包括医生和护士)是S，系统容量是c，受害者人数是无限的。因为系统是有限的，所以当系统有c个受害者的时候，再多的受害者就不会进入系统。最后，即使到达率大于服务率，系统都不会“爆炸”而会处于稳态。

关于系统的某些参数如下所述。系统服从“先到先服务”的服务规则。qj表示系统中有j个受害者的稳态概率。

(5)

等待时间服从j-c+1的爱尔朗分布，等待时间的分布函数表示如下：

在医院的受害者的平均等待时间表示如下：

(7)

因为，系统中不是所有的受害者都能在“黄金救治时间”被治疗，所以，我们通过公式(6)，即等待时间的分布函数计算出在“黄金救治时间”里能治疗的受害者的人数，从而预测医院能够治疗的受害者人数。

将(6)式展开整理得到公式(8)。(8)式表示等待时间小于等于1小时的概率。

(8)

4 实验

本节通过仿真验证上述提出的方法。4.1为到达率的仿真。4.2为医疗救助能力的仿真。

4.1 到达率的计算仿真

在恐怖袭击发生时，通过等式(4)，能够计算出每个时刻到达医院的受害者人数。假定生化袭击同时发生在北京复兴门地铁站的两个站台，离地铁站最近的医院北京二龙口医院就成为人们第一时间接受治疗的医院。红色标识B表示的就是二龙路医院。地铁站有A、B、C、D四个出口。B口是离医院最近的一个出口，D出口是距离医院最远的一个出口。由此可知第一个到达医院接受治疗的受害者最可能是从B口步行到达的。复兴门站距离医院的最近距离大概为833米。

图1

在早上7:30到9:00之间，北京地铁处于早高峰时段，若此时复兴门地铁站遭受生化恐怖袭击，将会有大量的人群涌入二龙口医院。根据地铁站与二龙口医院的地理距离以及遭受意外事故的受伤人群的步行能力，能够估算出最快到达医院的受害者的时间大概是15min。

早高峰期间，地铁一号线和二号线列车运行间隔都会缩短，列车进站的频率就会加快，站台的人数相应就会增多。另外，通过调查统计得到复兴门站早高峰时换乘地铁人数。采用高峰期7:30—8:30的客流调查数据，其具体数据如表1所示。由此看出此时复兴门站的人数(换乘的乘客)超过2万人次，平均每分钟的换乘人数超过400人。

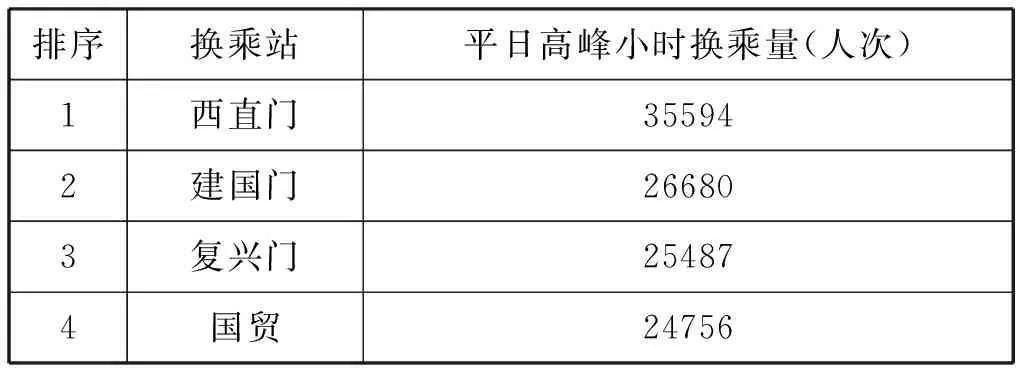
表1 高峰时段各个地铁站的换乘量

同时还会有大批的乘客通过入口到站台等待乘车，此时复兴门地铁站人数处于一个高峰值。所以，若此时发生恐怖袭击，地铁站有大概上千人，根据日本沙林毒气袭击事件报告可知，其中会有百分之三十左右的受害人会去医院。通过医院距离地铁站的距离和道路情况等因素，可以估算出受害者到达医院的速率，如表2所示。

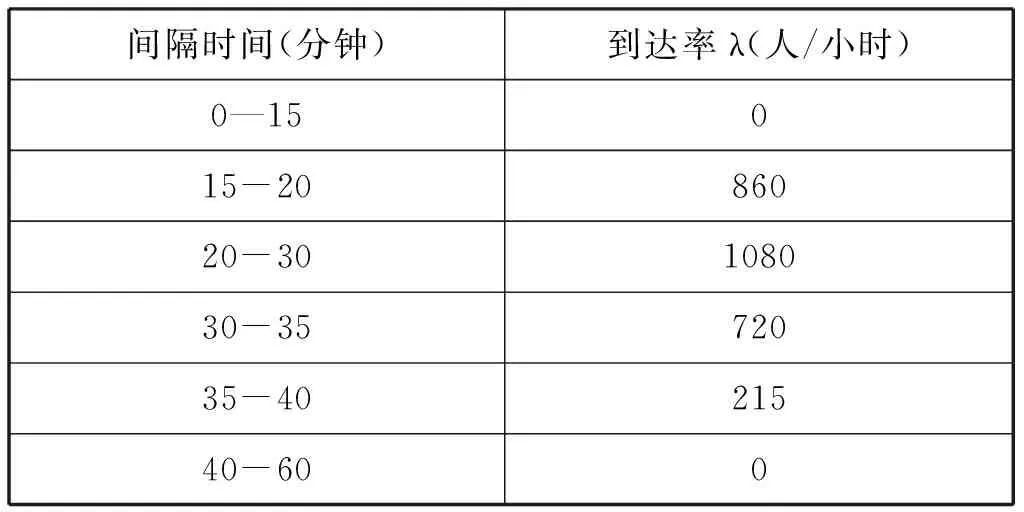
表2 不同时间受害者到达医院的速率λ

按照文献[3]的方法，可以通过等式(1)(2)(3)模拟出到达医院的受害者的概率分布。局部的结果如表3所示。

通过等式(4)可以计算出一小时内到达医院的受害者人数，其结果如图2所示。

图2 到达医院的受害者人数

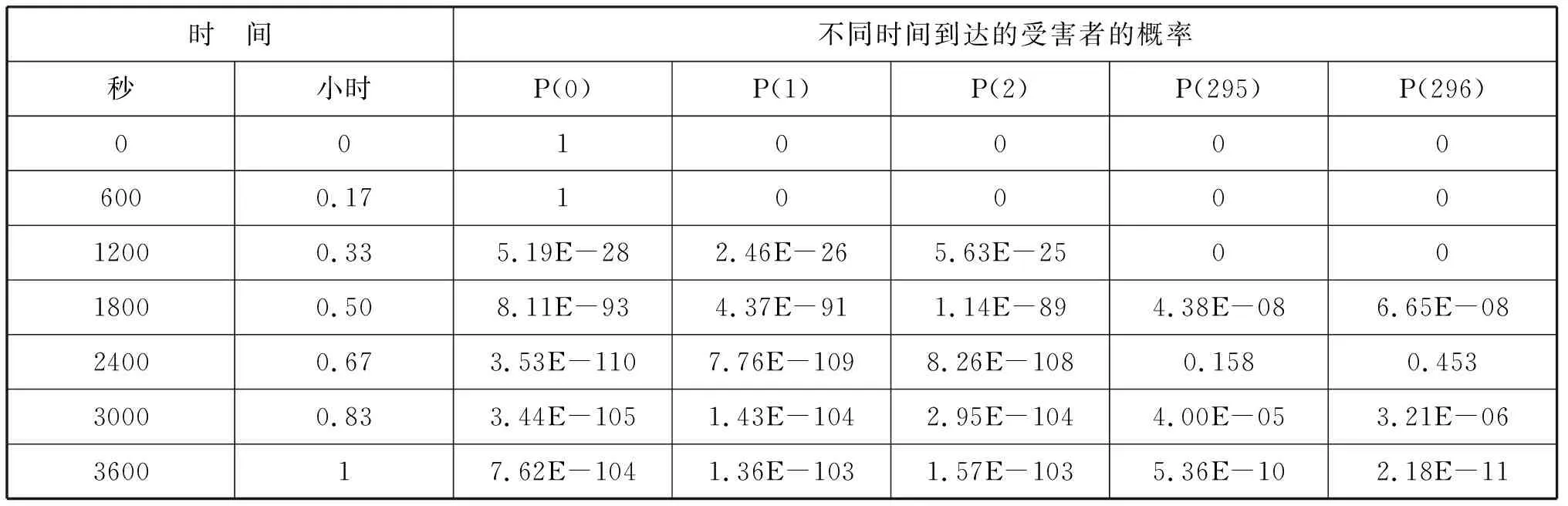
时 间不同时间到达的受害者的概率秒小时P(0)P(1)P(2)P(295)P(296)00100006000.171000012000.335.19E-282.46E-265.63E-250018000.508.11E-934.37E-911.14E-894.38E-086.65E-0824000.673.53E-1107.76E-1098.26E-1080.1580.45330000.833.44E-1051.43E-1042.95E-1044.00E-053.21E-06360017.62E-1041.36E-1031.57E-1035.36E-102.18E-11

条件：1.到达人数服从非齐次泊松分布。2.医院有十个医生，每小时可以治疗70个受害者。3.医院最多可以容纳296人。4.第一个受害者到达医院需要15分钟。

由上图可知，在第十五分钟，第一名受害者到达医院后，到达人数有明显的增长趋势。在一小时内有大约296个受害者到达医院，并且几乎所有的受害者都是在四十分内到达的。同时，随着受害者被不断被救助后，系统中的受害者在不断减少。仿真的结果与我们的经验是吻合的。

4.2 计算救助能力的仿真

本文中假设受害者到达医院后需要两个阶段的救治服务。首先，受害者在第一阶段需要填表登记并初步诊断其病情的轻重，无明显症状或病情轻微的患者进入观察室进行观察治疗，病情中度或严重的患者就必须接受下一个阶段的专业治疗。其中，病情中度者经过治疗，比如，打针输液，就可以出院。严重症状的患者则需要住院治疗。其次，在观察室的受害者中有部分人员目前症状比较轻微，一段时间后病情就会加重，需要进一步接受治疗，而观察室剩下的大部分人员在一段时间的观察后，未表现出严重症状，就可以离开医院。受害者到达医院的具体排队流程如图3所示。

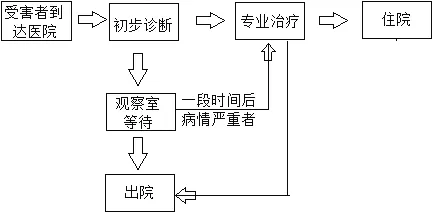
图3

假设到达医院的296名受害者在等候治疗。服务时间服从指数分布，在第一阶段的治疗过程中，有三名医生(即三个服务台)，每名医生每小时可以诊断60名受害者。第二个阶段，有七名医生(即七个服务台)，每名医生每小时只能救助3名受害者，并且等候区域能容纳所有受害者。根据(7)式和(8)式可以得出表4。

由表4可以看出在时间紧迫，医生人数有限的情况下，半小时内，3名医生只能诊断94人。一小时内，若要求救助率达到95%的话，只能救20人。

假如第一阶段设置的等待时间超过半小时，第二阶段的受害者人数就会相应增加，这就超出了此时医院的救助能力范围。所以，第一阶段设置的等待时间是半小时。

在日本沙林毒气发生后的官方报告中，我们得知，在发生袭击的第一天有640人到医院就诊，其中有111人(占就诊人数的17%)接受住院治疗。在对528人进行观察的过程中，有107人(占观察人数的20%)表现出中度的中毒症状，又从观察室到诊室接受治疗。有4人病情严重，住进了重度监护病房，还有1个人在急诊病房中不治身亡[5][6]。

表4 诊断人数及平均等待时间

在已有的数据下，我们做出如下分析。在诊断的94人中，有15%至20%的受害者(也就是16名左右的伤员)症状严重，需要到下一服务台接受治疗。剩下的受害者到观察室等待，这些在观察室的受害者中还会有大概20%(18名左右)的人员病情会加重，这些受害者依然得接受专业治疗。在救助率达到95%的前提下，第二个阶段安排7名医生完全可以救助最初症状严重的患者。

若一小时内，观察室的人员病情加重，也就是说此时病情严重患者多于20人。在初步诊治的阶段和专业治疗过程中，由于医疗能力限制，对于未能接受诊断和专业治疗的受害者。医院和突发事件指挥中心必须作出以下两种选择：1)尽快将他们转移到其他医院，其他的医院的救助能力也可以使用此方法计算；2)需要更多的医生救助这些受害者，可以从其他医院调来足够的医生救助受害者。当然，医院的救助条件也必须考虑在内(比如紧急病床数目、救援设备等等)，因此，最有效的办法是把受害者转移到其他医院接受治疗。

5 结论

文中，我们研究了当生化恐怖袭击发生时，受害者涌入首选医院的到达率以及医院的医疗救助能力。建立了一个瞬态系统，在这个系统中，紧急情况发生时可以通过排队论的方法求解所需数据。通过受害者的到达率和服务者的服务率的关系，能分别计算出每个时刻到达医院的受害者人数以及等候时间。

特别地，本文讨论了当λ>μ时，医院的医疗救助能力的计算，这种计算方法更符合生化应急方案及实际情况。当受害者的等待时间服从j-c+1的爱尔朗分布时，使用等待时间的概率分布函数可以计算出医院的医疗救助能力。

研究中已经举例证明了该方法的可行性。未来的研究包括瞬态行为模型的到达率函数的给出，并根据地点、时间、周围环境和事件中的其他条件，仿真出更符合实际情况的受害者的到达率，继续探讨复杂情况下的医院救治能力的预测。

[1]黄培堂. 如何应对生物恐怖[M].北京：科学出版社，2006.

[2]陈冀胜. 如何应对化学恐怖与化学毒性灾害[M].北京：科学出版社，2006.

[3]Wayne L Winston. 运筹学-概率模型应用范例与解法[M].北京：清华大学出版社，2006.

[4]唐应辉，唐小我. 排队论一基础与分析技术[M].北京：科学出版社，2006.

[5]Tetsu Okumura，Kouichiro Suzuki.The Tokyo Subway Sarin Attack: Disaster Management，Part 1:Community Emergency Response[J]. Academic Emergency Medicine，1998(5)：613-617.

[6]Tetsu Okumura，Kouichiro Suzuki.The Tokyo Subway Sarin Attack: Disaster Management，Part 2: Hospital Response[J]. Academic Emergency Medicine，1998(5)：618-624.