WCNS格式在梯形翼高升力构型模拟中的应用研究
李 松,王光学,王运涛,张玉伦,邓小刚
(1.空气动力学国家重点实验室,四川 绵阳 621000;2.中国空气动力研究与发展中心,四川 绵阳 621000;3.国防科学技术大学,湖南 长沙 410073)
WCNS格式在梯形翼高升力构型模拟中的应用研究
李 松1,2,王光学1,2,王运涛1,2,张玉伦1,2,邓小刚2,3
(1.空气动力学国家重点实验室,四川 绵阳 621000;2.中国空气动力研究与发展中心,四川 绵阳 621000;3.国防科学技术大学,湖南 长沙 410073)
采用5阶精度的有限差分格式 WCNS-E-5,对梯形翼高升力构型进行了数值模拟。研究了网格收敛性,WCNS格式对网格的依赖性更小。得到了与实验结果相一致的气动特性和压力分布。通过与一些著名CFD软件的计算结果比较表明,相比二阶格式,WCNS格式模拟高升力构型有明显优势,特别在失速迎角附近对流动结构的刻画更准确。同时,验证了程序对复杂外形的模拟能力和鲁棒性。
高升力构型;高阶精度;数值模拟;失速迎角;WCNS
0 引 言
由于增升装置对飞机的起飞着陆性能有重要影响,增升系统及其空气动力特性的研究一直是航空界的前沿课题。一般地,对于双发的大型商用飞机,起飞时的升阻比每提高1%,有效载荷能增加2800磅;着陆时的最大升力系数每增加1.5%,有效载荷能增加6600磅[1]。随着计算机软、硬件技术的迅猛发展和计算空气动力学研究的不断深入,CFD技术已经成为飞行器设计与评估的重要手段。基于雷诺平均Navier-Stokes方程的数值模拟软件几乎可以模拟所有复杂外形飞行器的绕流流场[2],但巡航状态数值模拟技术相对成熟,而高升力构型的数值模拟方法仍有待评估,面临诸多困难。通常,高升力构型是由缝翼、主翼和襟翼组成的多段翼系统,其搭接和缝道等形成的复杂性已经使得计算网格的生成变得很困难。而要模拟其包含有边界层转捩、流动分离与再附、尾迹与边界层相互作用等[3]复杂流动现象的绕流(如图1所示),对于CFD而言更是巨大的挑战。
为了正确评估并推进现有CFD模拟高升力系统的技术水平,国际国内先后组织了许多专题活动,如欧洲的EUROLIFT 项目[4],2010年6月AIAA 的第一届高升力预测研讨会(1st AIAA CFD High Lift Prediction Workshop,HiLiftPW-1)[5],国内在2009年组织了首届航空CFD可信度开放式专题研究活动(Aeronautics High Credible CFD Simulations Open Workshop,HiCFD)。梯形翼高升力构型是Hi Lift-PW-1和 HiCFD所选的标准模型。
高升力构型的数值模拟也是国内外学者关注的重点。Rumsey等[6]对近十五年来计算高升力系统的CFD方法进行了评估。朱自强等[7]对高升力系统数值模拟取得的成果、当前的水平以及存在的问题进行了阐述。Rumsey等[8]对 Hi Lift PW-1中提交的39组结果进行了比较和统计,评估了高升力构型数值模拟的当前水平,指出了需要进一步努力的方向。从已查阅的文献来看[4-10],当前高升力构型的数值模拟以二阶精度为主,高阶精度的模拟结果尚未看到。
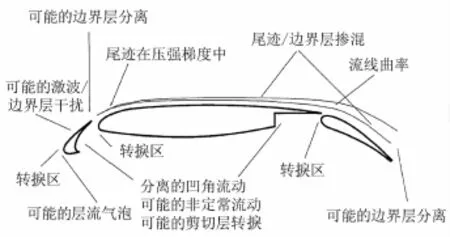
图1 三段翼型上可能呈现的流动现象Fig.1 Sketch of flow phenomena on a three-element airfoil
高升力构型绕流是典型的粘性主导的问题,这就要求数值方法能够准确地模拟物理粘性。二阶精度格式的数值粘性与物理粘性同是二阶项,数值粘性很容易污染物理粘性,进而造成较大的模拟误差。高阶精度格式耗散小,更适合模拟高升力构型流动问题。然而,现有的高阶精度格式多限于网格简单的问题,应用于复杂的工程问题仍有较大困难。原因在于,有限体积方法在复杂网格上容易实现,但是高阶精度格式的构造困难而且计算量太大。有限差分方法可以逐维操作,高阶精度格式容易构造且计算量小,但不容易满足守恒律,对网格质量要求较高,在复杂网格上实施比较困难。可以说,高阶精度格式应用于复杂外形的模拟是CFD研究中一项具有挑战性的工作。
WCNS格式[11-15]是邓小刚提出的 一 类 非 线 性高阶精度有限差分格式,具有高分辨率、低耗散、低色散和一致高阶精度等特点。自20世纪90年代以来,该团队就一直致力于高阶精度格式相关问题的研究,在格式、算法和应用等方面取得了突破性进展。文献[16]针对高阶有限差分算法在满足几何守恒律方面的困难,发展了满足几何守恒律的高阶精度的坐标变换导数算法,大大提高了 WCNS格式对复杂网格的适应性和鲁棒性。
本文对流项采用5阶精度的 WCNS-E-5格式离散,粘性项采用6阶精度的中心格式离散,对梯形翼高升力构型进行了数值模拟。研究了网格收敛性;得到了与实验结果一致的气动特性和压力分布;研究了初始条件对失速迎角的影响。通过与一些著名CFD软件的计算结果比较表明,相比二阶格式,WCNS格式模拟翼梢涡的能力更好,对流动结构的刻画更准确。同时,也验证了程序对复杂外形的模拟能力和鲁棒性。
1 计算方法
控制方程为雷诺平均N-S方程+SST两方程湍流模型,对流项的离散采用WCNS-E-5格式,粘性项的离散采用6阶精度中心格式,离散方程采用LUSGS求解。计算中采用了并行技术加速。
1.1 控制方程
曲线坐标系下,雷诺平均N-S方程为:
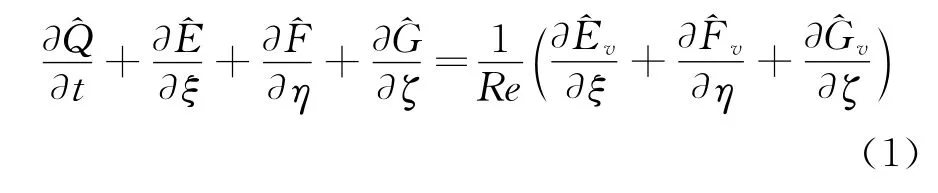
1.2 对流项离散格式
对流项离散采用原始变量型的WCNS-E-5格式,记网格间距为h,以ξ方向为例:
1)内点格式
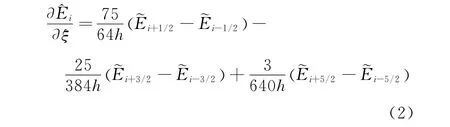
2)边界和靠近边界格式
以格点0表示左边界,以格点N 表示右边界,则左边界和靠近左边界格式如下:
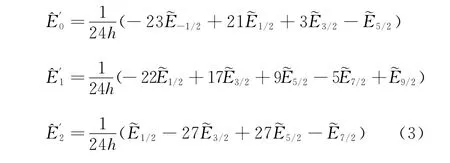
在N 点附近的右边界格式与上式类似。
由于WCNS格式在文献[11-14]有详细描述,相关的插值公式及粘性项离散格式在这里不再赘述。坐标变换导数的计算使用了满足几何守恒律的高阶精度的算法,文献[16]中有详细描述。
2 计算网格及状态
2.1 计算网格
高升力构型是安装在机身上的大弦长、半展、三段构型,机翼没有扭转、没有上反角,采用大弦长和相对较小展弦比。风洞实验设计了两种襟翼构型,一种为全展长襟翼,单缝襟翼从翼梢一直延伸到翼根,并融于机身;另一种为半展长襟翼,襟翼的展长大约占模型展长的1/2,并置于机翼的中间位置。以上两种襟翼构型具有相同的前缘缝翼,缝翼从翼梢一直延伸到翼根,并融于机身。本文中计算的是全展长襟翼构型。
CFD计算有两组稍微不同的数模可以使用,一组是梯形翼的原始CAD数据(as-designed),一组是2002年质量保证(QA)重新检测的数据(as-built)[17]。本文使用的数模采用2002年重新检测的数据。
按照HiLiftPW-1给出的网格指导[18],本文使用Ansys公 司的 ICEM 软 件生 成了 相同 拓扑 的 粗(Coarse)、中 (Medium)、细 (Fine)三 套对 接网格(point-to-point),均为369块。网格使用H 型拓扑,边界层网格采用O型拓扑。图2给出了中等网格的网格拓扑、表面网格分布以及细节处理。三套网格的详细统计信息如表1所示。
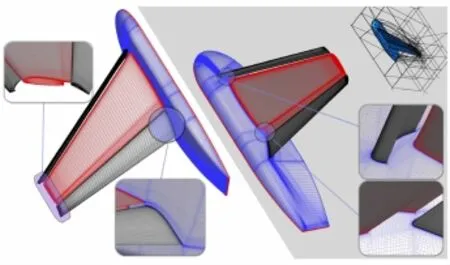
图2 高升力构型中等网格Fig.2 Medium grids for high-lift configuration
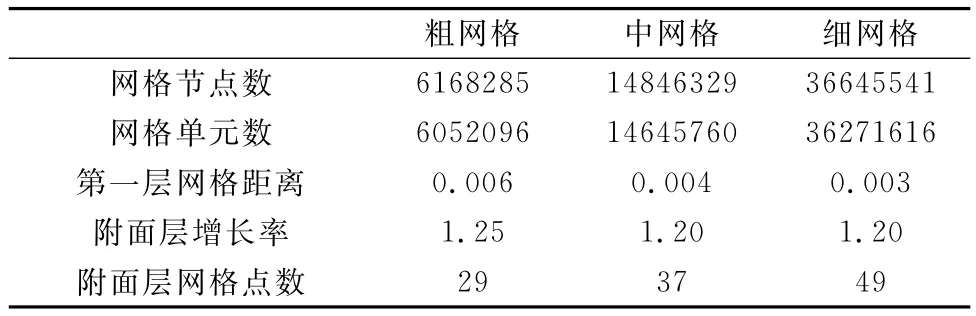
表1 网格统计表Table 1 Grid statistics
2.2 计算状态
梯形翼模型分别于98/99年和02/03年做了两组实验[17],如图3所 示。前一组实验 称为梯形翼实 验(Trapezoidal Wing Experiment),涵盖多个雷诺数下的一系列的构型。后一组实验称为3D高升力流动现象实验(3-D High-Lift Flow Physics Experiment),更关注特定雷诺数(4.3×106)下的详细的流动现象。

图3 梯形翼高升力构型模型Fig.3 Fullspan model of high-lift trapwing configuration
两次实验为CFD研究高升力构型的流动现象提供了丰富的数据,在本文的计算中来流参数如下:

3 计算结果
按照HiLift-1的要求,本文中初始流场均使用自由来流,并采用全湍流进行模拟。本文计算的结果与T513次实验以及多个著名CFD软件计算的结果进行了比较(相关数据均来自 Hi Lift PW-1官方网站[18]),需要指出的是CFX使用转捩模型进行模拟。
图4给出了中等网格下典型迎角的收敛历程曲线。四个计算状态的残差都迅速地下降了四个量级。升力系数基本稳定,计算已经收敛。这表明计算中几何守恒得到了满足。同时,也表明本文的计算方法对复杂网格具有良好的适应性。

图4 高升力构型的收敛历程曲线Fig.4 Convergence histories of high-lift configuration
3.1 网格收敛性
为了排除网格对计算结果的影响,对13°和28°两个迎角进行了网格收敛性分析。图5给出了网格收敛性的结果。可以看出,在13°迎角下本文计算的升力随网格加密是单调收敛的,而28°迎角下本文计算的升力随网格加密有一个波动,是振荡收敛的。
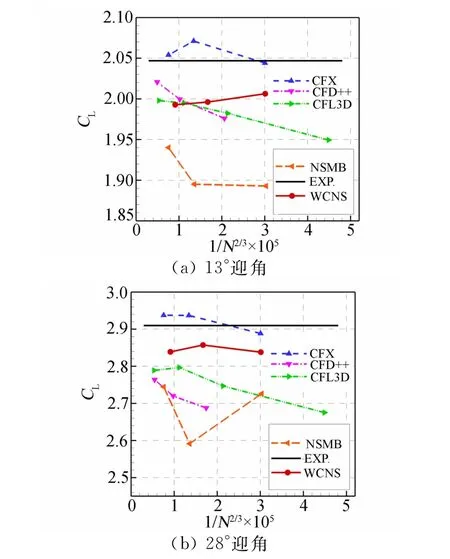
图5 高升力构型的网格收敛性曲线Fig.5 Grid-convergence of high-lift configuration
为了研究网格对计算结果的可信度的影响,表2给出了13°迎角下的Richardson外插值、基于外插值的相对误差和网格收敛指标(Grid Convergence Index,GCI)。Richardson外插方法是Richardson于1910年首次使用[19],基于已有网格的计算结果(要单调收敛)可以外推得到空间步长h趋于0时的结果。网格收敛指标由 Roache提出[20],它是一种网格细化效果的统一度量方法,度量参数中引入了网格细化率r和收敛阶p。相关计算公式可见文献[21]。
从表2中可以看出,本文计算的结果是单调收敛的,实际收敛精度阶高于其它计算结果,基于Richardson外插值的相对误差远远小于其他计算结果。对于网格收敛指标 GCI,细网格指标GCI12均小于中网格指标GCI23,本文计算的结果小于其它计算结果的对应指标。这表明本文使用的网格对计算结果影响较小,计算结果可信度较高。
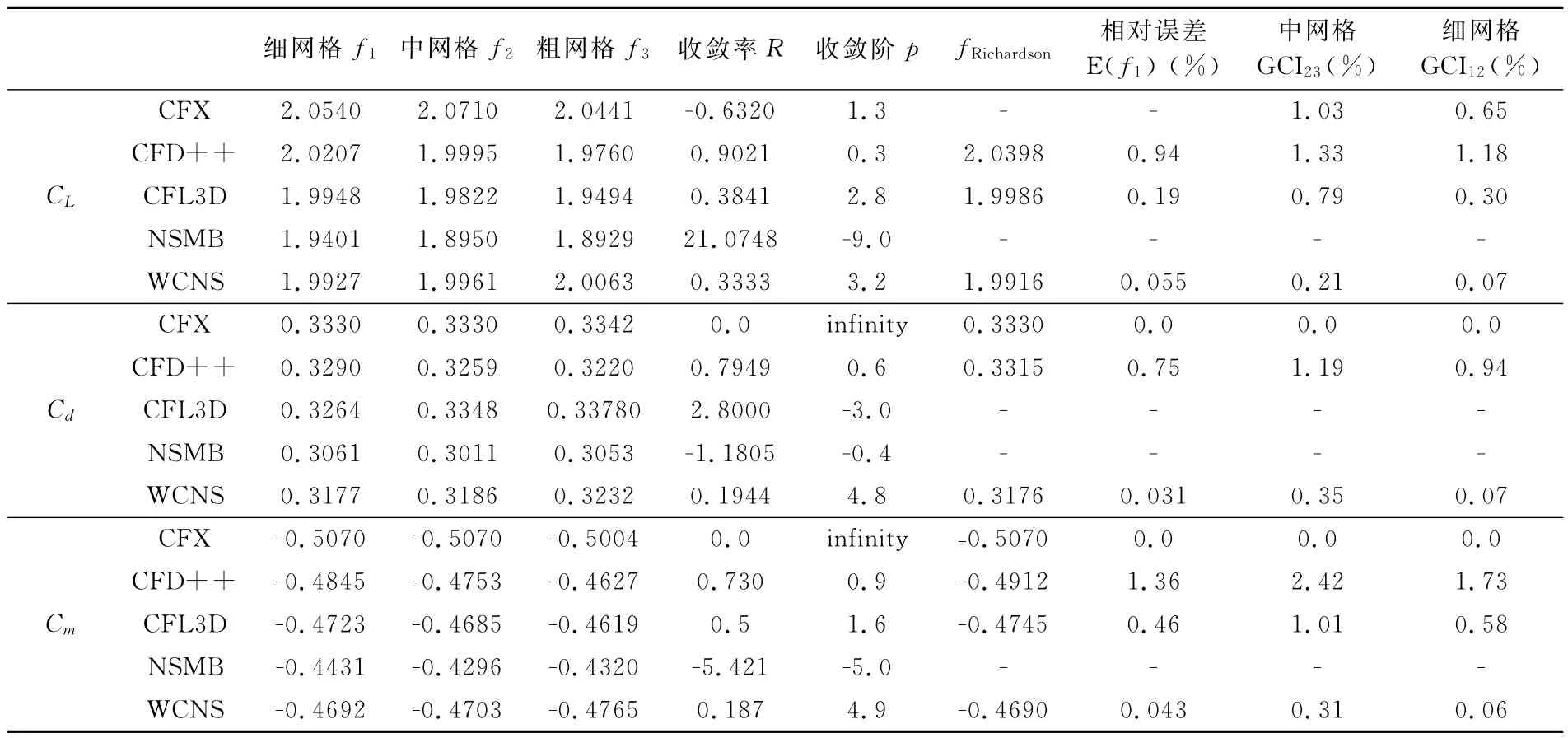
表2 13°迎角的Richardson外插和网格收敛指标Table 2 Richardson extrapolation and grid convergence index atα=13°
3.2 力特性比较
图6是中等网格计算的气动力系数。由图中可见,本文的计算结果与实验一致性很好。相对于其它典型软件的计算结果,更接近实验值,在非线性段特别是失速迎角附近,WCNS格式优势更明显。
相对于实验数据,本文计算的升力系数和阻力系数整体偏小,这与计算中没有使用转捩模型有关。根据文献[22]的结果,使用转捩模型后,边界层厚度减小,升力系数和阻力系数都会增加。图6中易见,使用转捩模型的CFX的计算结果,在线性段更接近实验值。这也表明了开展高升力构型模拟的转捩研究的潜在必要性。
在飞行器/机翼的俯仰振荡、动失速等过程中,其流场特征不仅与特定状态有关还与到达该状态的动态过程(如角速率等)有关,这被称为迟滞现象(hysteresis)。静失速过程中特定状态的流场的特征会依赖于其历史状态[23],迎角增加过程和迎角减小过程得到的同一迎角的(定常)流动的特征不相同,这也被称为迟滞现象。高升力构型的实验中在静失速迎角附近出现了后一种迟滞现象。数值计算中发现,在失速迎角附近,不同的初场或算法可能导致不同的流场演化过程,进而导致不同流态的结果,文献[22]也提到了这种现象。图6中同时给出了 WCNS格式使用自由来流和小迎角解作为初场得到的结果。从图中可见,自由来流初场计算的失速迎角为35°,小迎角解初场计算的失速迎角为37°,分别与T513实验中迎角减小(r106)、迎角增大(r105)过程所测得的失速迎角是一致的。这表明本文的结果对失速迎角的预测更为准确。
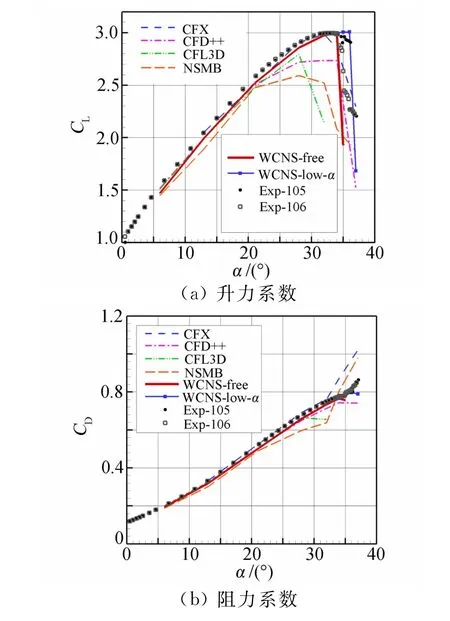
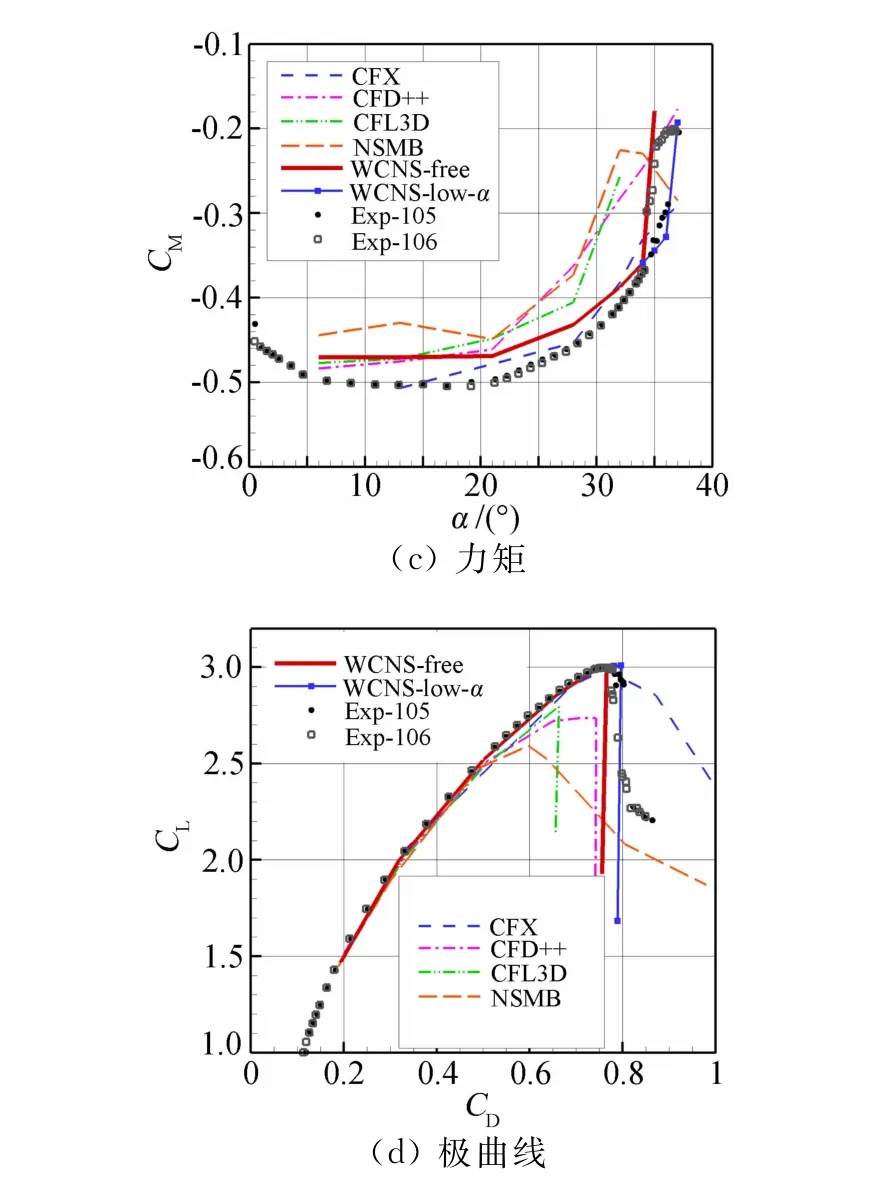
图6 高升力构型的气动系数曲线Fig.6 Aerodynamics characteristic of high-lift configuration
3.3 表面压力分布及空间流场模拟
图7给出了13°、21°、28°和34°四个迎角表面压力分布云图以及表面流线。由图中可见,各迎角下,主翼上弦向流动是最主要的,只在翼梢附近的小范围内出现展向流动;随着迎角的增加,主翼上的吸力峰显著提高,襟翼上表面的分离区则逐渐减小以至完全消失,从而升力增大。由图中还可以看到34°迎角时主机翼和襟翼上都能够维持附着流动的状态,没有大范围的分离。
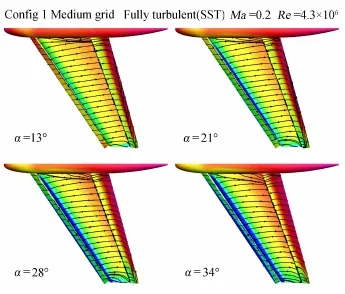
图7 高升力构型的表面压力分布云图及表面流线Fig.7 Surface pressure distribution and streamlines of high-lift configuration
图8给出了34°迎角计算的翼梢涡的形态。图9给出了28°和34°迎角三个典型站位上的压力分布。从压力分布对比来看,在机翼中段站位上,各计算结果的压力分布与实验值都符合得较好。在靠近翼梢的位置,二阶格式的计算结果严重偏离实验值,而高阶的WCNS格式仍能给出与实验值基本相符的预测,包括是接近失速的34°迎角。
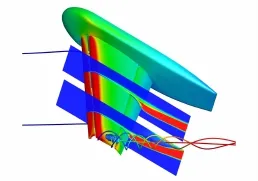
图8 34°迎角计算的翼梢涡Fig.8 Wing-tip vortex under 34°AOA
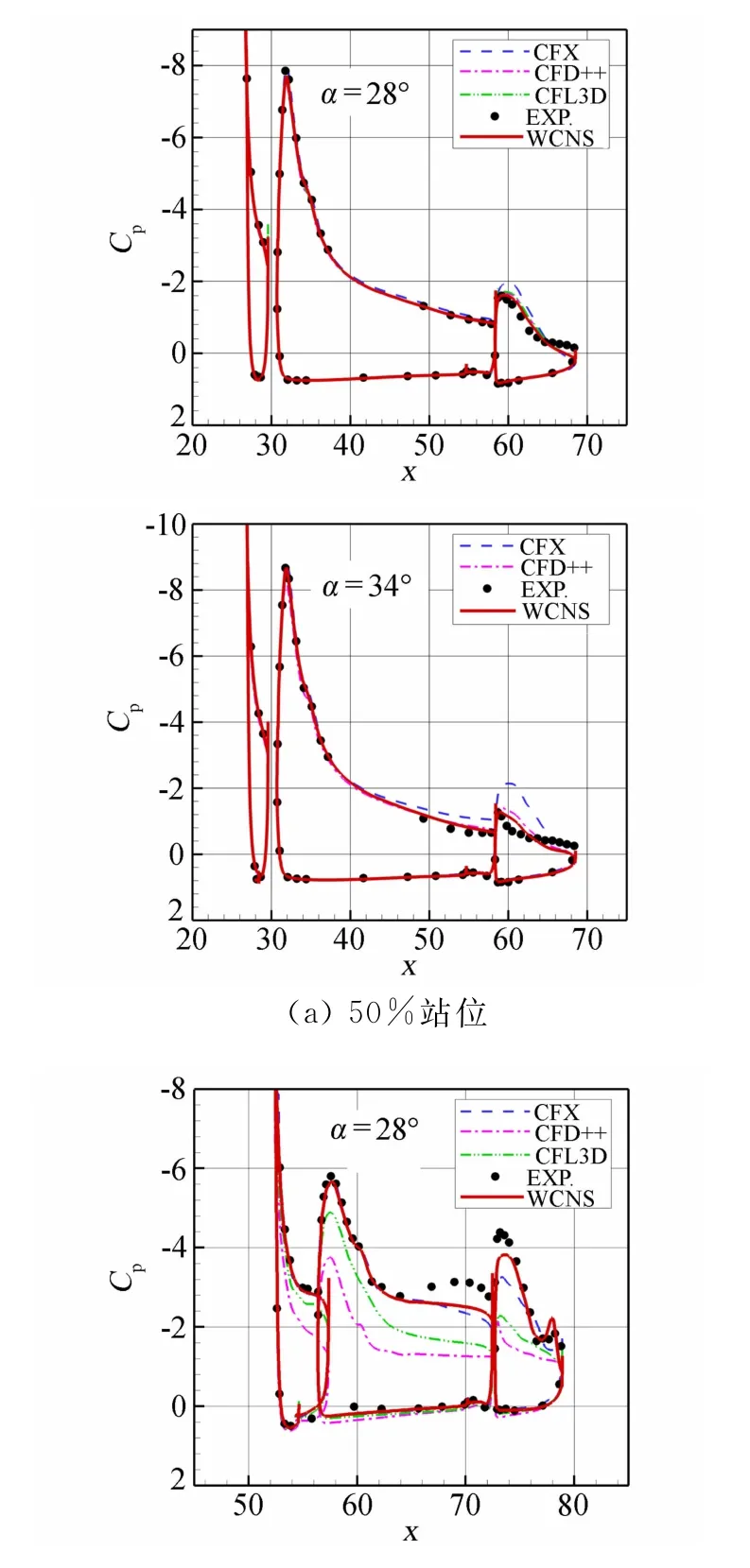
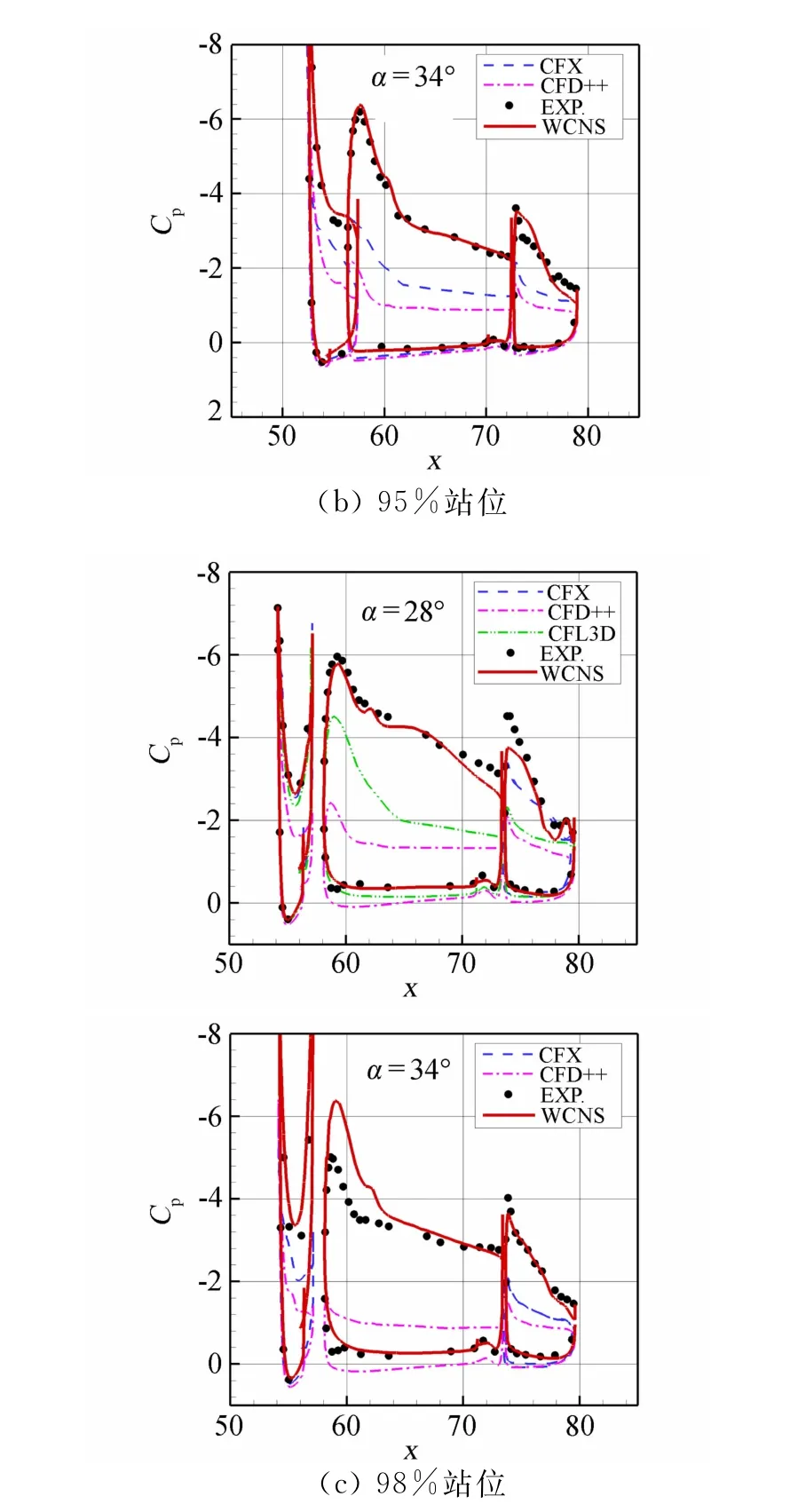
图9 典型站位表面压力系数的比较Fig.9 Cpdistribution for typical wing stations
文献[8]指出,靠近主翼翼梢区域的流场很难预测,而准确、成功地捕捉翼梢涡是预测这些位置的表面压力分布的非常重要的因素。对于翼梢附近的流动,二阶精度格式难以准确捕捉翼梢附近流场的急剧变化。而高阶精度格式的精度更高、数值粘性更小,可以显著地减小二阶精度格式的不足,对翼梢附近流动的模拟更准确,能够准确地捕捉翼梢涡,对这些位置的表面压力分布预测得较好。
4 结 论
本文采用高阶精度WCNS-E-5格式,对梯形翼高升力构型进行了数值模拟,研究了网格收敛性,并对计算结果进行了较为细致的分析。相比二阶精度格式,WCNS格式有以下特点:
(1)得到了网格收敛解的结果;对网格的依赖性更小;
(2)气动特性与实验值具有很好的一致性;模拟大迎角流动更有优势,对失速迎角的预测更准确;
(3)对翼梢附近的流动结构模拟得更准确,表面压力分布与实验值符合得更好;
(4)高阶精度的WCNS格式更适合模拟高升力构型绕流问题;
(5)程序对复杂网格的适应能力比较强,收敛性比较好,比较鲁棒。
[1] MEREDITH P T.Viscous phenomena affecting high-lift systems and suggestions for future CFD development,high-lift systems aerodynamics[R].AGARD CP 315,1993,191-198
[2] TINOCO E N,BOGUE D R.Progress toward CFD for Full flight envelope[J].Aeronautical Journal,2005,109(1100):451-460.
[3] SMITH A M O.High lift aerodynamics[J].Journal of Aircraft,1975,12(6):501-530.
[4] HANSEN H ,THIEDE P,MOENS F,et al.Overview about the Europe high lift research program EUROLIFT[R].AIAA 2004-0767.
[5] SLOTNICK J P,HANNON J A,CHAFFIN M.Overview of the first AIAA CFD high lift prediction workshop (invited)[R].AIAA 2011-862.
[6] RUMSEY C L,YING S X.Prediction of high lift:review of present CFD capability[J].Progress in Aerospace Science,2002,38(2):145-180.
[7] ZHU Z Q,CHEN Y C,WU Z C,et al.Numerical simulation of high lift system configration[J].ACTA Aeronautica et Astronautica Sinica,2005,26(3):257-262.(in Chinese)朱自强,陈迎春,吴宗成,等.高升力系统外形的数值模拟计算[J].航空学报,2005,26(3):257-262.
[8] RUMSEY C L,LONG M,STUEVER R A,et al.Summary of the first AIAA CFD high lift prediction workshop (invited)[R].AIAA 2011-939.
[9] HONG J W,WANG Y T,PANG Y F,et al.Numerical research of high-lift configurations by structured mesh method [J].ACTA Aerodynamica Sinica,2013,31(1):75-81.(in Chinese)洪俊武,王运涛,庞宇飞,等.结构网格方法对高升力构型的应用研究[J].空气动力学学报,2013,31(1):75-81.
[10]WANG Y T,HONG J W,MENG D H.The influence of turbulent models to trapwing simulation[J].ACTA Aerodynamica Sinica,2013,31(1):52-55.(in Chinese)王运涛,洪俊武,孟德虹.湍流模型对梯形翼高升力构型的影响[J].空气动力学学报,2013,31(1):52-55.
[11]DENG X G,MAEKAWA H,SHEN C.A class of high order dissipative compact schemes[R].AIAA 96-1972.
[12]DENG X G,MAO M L.Weighted compact high-order nonlinear schemes for the Euler equations[R].AIAA 97-1941.
[13]DENG X G,ZHANG H X.Developing high-order weighted compact nonlinear schemes[J].Journal of Computational Physics,2000,165:24-44.
[14]DENG X G.High-order accurate dissipative weighted compact nonlinear schemes[J].Science in China (Series A),2002,45 (3):356-370.
[15]DENG X G,MAO M M,TU G H,et al.Extending the fifthorder weighted compact nonlinear scheme to complex grids with characteristic-based interface conditions[J].AIAA Journal,2010,48(12):2840-2851.
[16]DENG X G,MAO M M,et al.Geometric conservation law and applications to high-order finite difference schemes with stationary grids[J].Journal of Computational Physics,2011,230:1100-1115.
[17]HANNON J A,WASHBURN A E,JENKINS L N,et al.Trapezoidal wing experimental repeatability and velocity profiles in the 14-by-22-foot subsonic tunnel(invited)[R].AIAA 2012-0706.
[18]http://hiliftpw.larc.nasa.gov/index-workshop1.html
[19]RICHARDSON L F.The approximate arithmetical solution by finite differences of physical problems involving differential equations with an application to the stresses in a masonry dam [J].Transactions of the royal society of London(Series A),1908,210:307-357.
[20]ROACHE P J.Perspective:a method for uniform reporting of grid refinement studies[J].ASME Journal of Fluids Engineering,1994(116):405-413.
[21]OBERKAMPF W L,ROY C J.Verification and validation in scientific computing[M].Cambridge University Press,2010.
[22]SCLAFANI A J,SLOTNICK J P,VASSBERG J C.Extended OVERFLOW analysis of the NASA trap wing wind tunnel model[R].AIAA 2012-2919.
[23]YANG Z F,IGARASHI H,MARTIN M,et al.An experimental investigation on aerodynamic hysteresis of a low-Reynolds number airfoil[R].AIAA 2008-0315.
Numerical simulation of high lift trapezoidal wing configuration with WCNS-E-5 scheme
LI Song1,2,WANG Guangxue1,2,WANG Yuntao1,2,ZHANG Yulun1,2,DENG Xiaogang2,3
(1.State Key Laboratory of Aerodynamics,Mianyang Sichuan 621000,China;2.China Aerodynamics Research and Development Center,Mianyang Sichuan 621000,China;3.National University of Defense Technology,Changsha Hunan 410073,China)
High order accuracy numerical simulations for flows of high lift trapezoidal wing configuration were performed by solving Navier-Stokes equation together with SST two-equation turbulence model.In the study,WCNS-E-5 scheme was utilized in the discretization of convection terms,while 6thorder central difference scheme for viscous term.Grid convergence result was obtained,which was in good agreement with test data,and WCNS scheme was less dependent on mesh density than 2ndorder scheme.Compared with other computational results obtained by typical CFD solvers,both the force coefficients and the surface pressure distributions given in this paper shown better accordance with the test data,and more reasonable prediction of flow structure near stalling was obtained.As revealed from these results,WCNS scheme took higher accuracy order and was more suitable for simulation of flow around high lift configurations than 2ndorder scheme.The capability and the robustness of the program to simulate complex high lift configurations were confirmed.
high lift configuration;high order scheme;numerical simulation;stalling angle;WCNS
V211.3
Adoi:10.7638/kqdlxxb-2012.0188
0258-1825(2014)04-0439-07
2012-11-12;
2013-09-05
国家重点基础研究发展计划(973计划,2014CB744803.2)
李 松(1982-),男,助理工程师。研究方向:计算空气动力学.E-mail:lisonic@foxmail.com
李松,王光学,王运涛,等.WCNS格式在梯形翼高升力构型模拟中的应用研究[J].空气动力学学报,2014,32(4):439-445.
10.7638/kqdlxxb-2012.0188. LI S,WANG G X,WANG Y T,et al.Numerical simulation of high lift trapezoidal wing configuration with WCNS-E-5 scheme[J].ACTA Aerodynamica Sinica,2014,32(4):439-445.

