基于动网格高空长航时机翼优化
朱雄峰,郭 正,侯中喜
(国防科技大学 航天科学与工程学院,湖南 长沙 410073)
基于动网格高空长航时机翼优化
朱雄峰,郭 正,侯中喜
(国防科技大学 航天科学与工程学院,湖南 长沙 410073)
分析了机翼设计优化的一般策略,针对高空长航时飞行器的气动性能需求和机翼构型特点,提出以机翼剖面翼型沿展向分布的设计优化;针对Hicks-Henne翼型参数化方法后缘不光顺的缺陷,提出了改进Hicks-Henne翼型参数化方法;针对通常基于线性插值的三维动网格生成方式的缺陷,提出采用基于B样条函数的三维动网格生成;通过对商业软件Pointwise和Fluent的二次开发实现数据流和工作流的定制及自动化,并将所有流程在iSIGHT平台下集成;优化算例表明,基于动网格的机翼优化实现提高功率因子的目标,是高空长航时机翼优化中的一种有效方法。
高空长航时飞行器;动网格;机翼优化;CFD;B样条
0 引 言
“飞机设计,气动先行”,航空飞行器机翼无论在结构上还是功能上都是其最重要的部分之一,翼型和机翼的设计始终是飞行器气动设计的热点和核心技术。机翼的设计和优化目标往往是提高升力系数CL、减小阻力系数CD、提高升阻比CL/CD、提高功率因子C1.5L/CD等。论文研究针对高空长航时 飞行器(High Altitude Long Endurance Aircraft,HALE Aircraft),此类飞行器机翼的显著特点是大展弦比平直机翼,如美国全球鹰(Global Hawk)展弦比达25,1/4弦线5°54′小后掠,美国太阳神(Helios)展弦比更达30.9且无后掠。对大展弦比平直机翼常采用的优化策略有:精简控制面保持气动结构的完整性;机翼平面形状优化如椭圆机翼平面、机翼面积、展弦比、根梢比和后掠角的优化;机翼三维形状的优化如剖面翼型、上反角、扭转轴和扭转角、相对厚度分布的优化。国内外对机翼设计优化进行过广泛的研究:文献[1]提出基于Kriging代理模型和改进粒子群算法的机翼优化;文献[2]研究了跨声速自适应机翼的优化方法;文献[3-4]提出以机翼厚度分布和扭转角为设计变量的三维机翼优化;文献[5]提出采用简化后二阶响应面模型进行翼型和机翼的气动优化设计;文献[6]研究了基于多水平Co Kriging代理模型的翼型和机翼多点优化;文献[7]研究了基于并行 Newton-Krylov算法的机翼优化。
在机翼优化方法中基于代理模型的优化,需要在优化流程开始之前采样一定数量的试验设计样本并构造代理模型,代理模型取代真实物理模型进行优化其精度不仅取决于代理模型的选择,更依赖于试验样本集数量的支持,以二阶响应面模型为例其最小样本集为(n+1)(n+2)/2其中n为设计参数数量,上式表明样本集数量随设计参数数量是平方关系增长,对机翼设计优化过程中往往涉及几十上百个参数的多参数优化过程,甚小的试验设计样本集不能准确描述整个高维设计空间从而造成优化结果失真,较大的样本集则需消耗巨大的CFD计算代价以及人工采样时间,为此本文采用基于动网格的机翼设计优化,即将机翼参数化建模、动网格变形、CFD流场计算等复杂过程自动化。众所周知,续航时间长是高空长航时飞行器的主要性能优势和追求目标,为此国内外广泛开展了高燃油经济性能的航空发动机以及采用可再生能源的太阳能飞行器如太阳神(Helios)、微风(Zephyr)、阳光动力号(Solar Impulse)等,特别地,高空长航时飞行器的续航能力还与飞行器的气动性能紧密相关,显然在平飞飞行条件下,平飞功率越小续航时间越长,而飞行器平飞功率消耗与功率因子是反比关系,因此本文以 提 高功率 因子C1.5L/CD为设计目标,以机翼三维参数化布局为设计变量,探寻满足一定飞行工况下的对应最大续航能力的机翼三维布局。
1 总体思路
机翼气动力布局设计是把选定的翼型以适当的方式组合形成三维机翼,即将选定的翼型以适当的最大厚度和几何扭转角沿展向分布而形成三维机翼[3]。对高空长航时HALE飞行器,为减小诱导阻力提高升阻比,机翼平面形状常用大展弦比无后掠平直机翼,在概念设计阶段机翼平面的拓扑形状已经选定,本文选择机翼剖面翼型分布为设计变量:即沿机翼展向0.0、1/3、2/3、1.0倍半展长分别选取控制截面,在原始翼型的基础上对上述截面的翼型进行参数化控制,如图1所示。考虑到现有工程实践中机翼三维几何构型CAD往往由B样条函数产生,为使优化过程中机翼形状符合实际构型,机翼三维网格构型亦由上述4个控制截面按B样条函数生成。
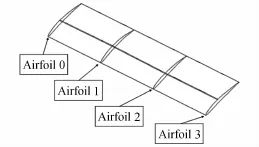
图1 控制截面分布Fig.1 Display of wing control profile
本文基于动网格机翼优化的基本流程主要由三个模块组成:首先是动网格生成模块,该模块由C语言编程实现,模块的输入文件是控制截面翼型Hicks-Henne参数化方法描述文件Hicks.dat,输出文件是依 据Hicks-Henne参数 化方法 变形后 的Plot3D格式网格文件 Out Mesh.x,同时还需要辅助文件:机翼初始网格的Plot3D文件in Mesh.x;第二个模块是边界条件生成模块,该模块通过对商业软件Pointwise二次开发实现,其输入文件是上一模块的输出文件即变形后网格文件,输出文件是加入边界条件可直接用于CFD计算的CAE文件 Wing.cas,同时该模块还需要辅助文件:Pointwise边界条件定义Glyph2脚本文件 Glyph2.glf;第三个模块是流场解算模块,该模块通过对商业软件Fluent的二次开发实现,该模块的输入文件是上一模块的输出文件即Wing.cas文件,输出文件是升力系数和阻力系数的迭代历史文件即cl-history和cd-history;上述三个模块由商业集成平台iSIGHT实现流程定制,以流场解算模块的计算结果形成设计目标,并以控制截面翼型参数化描述文件为设计变量。图2所示是总体流程示意图。
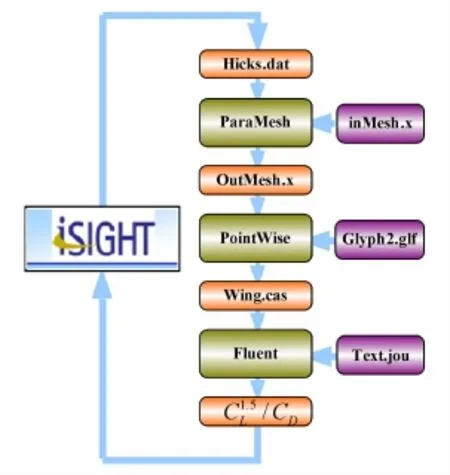
图2 总体流程Fig.2 The overall process
2 动网格过程
2.1 机翼剖面翼型参数化
控制截面翼型参数化过程将翼型的几何外形用连续光滑的数学函数描述,常用的翼型参数化方法有Hicks-Henne形函数方法、正交基函数法、CST 方法、Bezier曲线参数化、PARSEC参数化方法等。上述参数化方法中,Hicks-Henne形函数方法是小扰动方法,即在基准翼型上叠加小扰动函数得到新的翼型,该方法天然适用于本文基于基准翼型的动网格方法[8-11]。
Hicks-Henne翼型的形状由基准翼型和扰动形函数的线性叠加决定。翼型用基准翼型、形函数及其系数定义。一般选用的是Hicks-Henne形函数fk(x)

式中,e(k)=ln0.5/ln xk,0≤xk≤1。取xk(k=1,2,3,4,5,6)分别为0.15,0.3,0.45,0.6,0.75,0.9以形函数的系数作为设计变量,与基准翼型一起确定新翼型形状,并且选用12个设计变量D=[a1,…,a12]表示翼型的坐标如下式
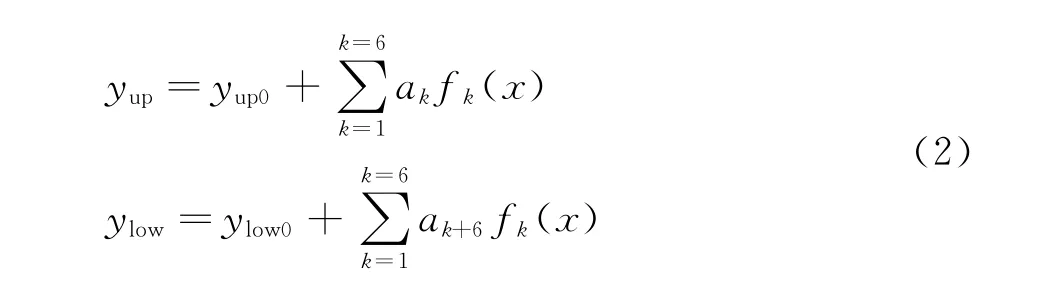
式中:yup,ylow分别为 新 翼 型 的 上、下表面 纵 坐 标;yup0、ylow0分别 为 基 准翼型的上、下 表面纵坐标;k、a分别为控制翼型形状的参数个数和系数。12个设计变量的取值范围不超过±0.01。如图3(a)所示是由拉丁超立方随机生成4组设计变量得到的Hicks-Henne翼型曲线。
由图3(a)中可以看出 Hicks-Henne翼型后缘并不光顺且出现了拐点,这显然不符合翼型设计的物理需求,为解 决该 问 题引 入 扰动函 数φ(x)=xNnose· (1-x)Naft,并附 加 扰 动 增益 函数 得φ(x)=xNnose·其 中N nose为控 制前 沿 的 扰 动量参数,N aft控制翼型后缘扰动量参数,由图3(b)可以看出扰动函数的扰动增益与N nose和N aft负相关,为使该扰动函数对翼型前缘影响较小而对翼型后缘影响较大,选择N nose=0.75,N aft=0.1,将该形函数代替原始 Hicks-Henne形函数中k=6项,得到新的Hicks-Henne形函数如式(3)。采用图3(a)所述相同的4组拉丁超立方设计变量得到新的 Hicks-Henne翼型曲线如图3(c),图中可以看出改进后翼型后缘较原始曲线较为平滑。
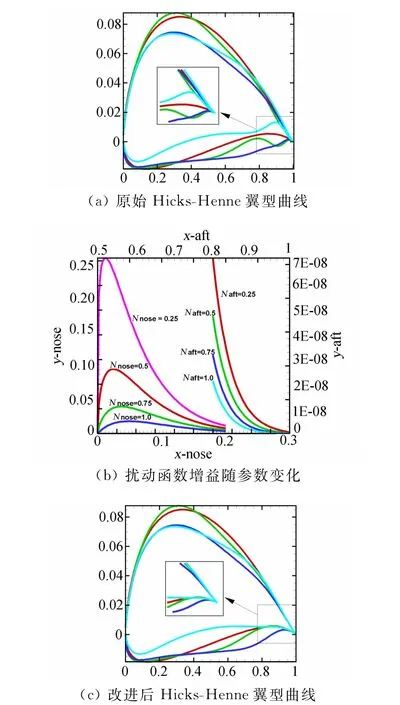
图3 Hicks-Henne改进示意图Fig.3 Improvement of Hicks-Henne parameterization

2.2 机翼三维构型参数化
选定控制截面并参数化翼型后,通常采用线性插值形成三维网格,然而该构型与工程实际CAD构型有较大误差,本文依据B样条函数生成三维机翼沿展向任一截面的形状,由B样条性质:若控制点个数n与B样条基数p满足n=p且节点矢量U={0,…,0,1,…,1},那么C(u)是Bezier曲线,考虑到截面数量往往是一个小量,Bezier曲线代替B样条不致阶数过高且有利于简化计算[12]。
Bezier曲线是由一组折线集,或称之为Bezier特征多边形来定义的。曲线的起点和终点与该多边形的起点、终点重合,且多边形的第一条边和最后一条边表示了曲线在起点和终点的切矢量方向。曲线的形状趋于特征多边形的形状。当给定空间n+1个点的位置矢量Pi,则Bezier曲线上各点坐标的插值公式是
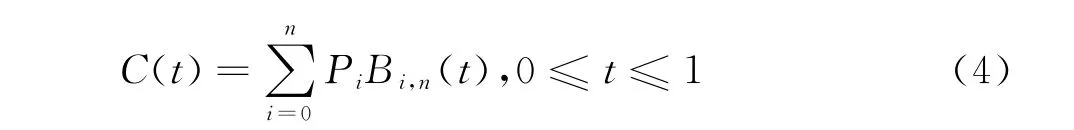
Pi构成该曲线的特征多边形,Bi,n(t)是Bernstein基函数,也是曲线上各点位置矢量的调和函数。
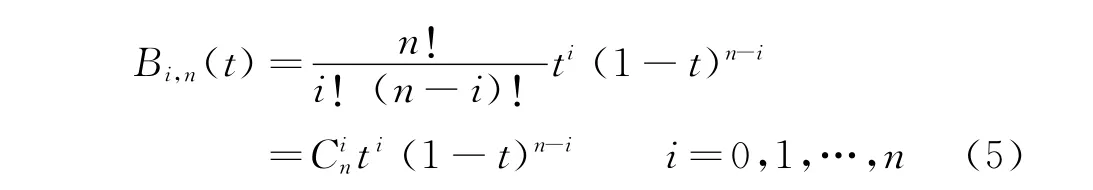
反算Bezier曲线控制点:若给定n+1个型值点Qi(i=0,1,…,n),要求构造一条Bezier曲线通过这些点。通过Qi的Bezier曲线的控制点Pi(i=0,1,…,n)通常可以按如下方式求解:取参数t=i/n与点Qi相对应用以反算Pi。设Qi在曲线C(t)上,且有
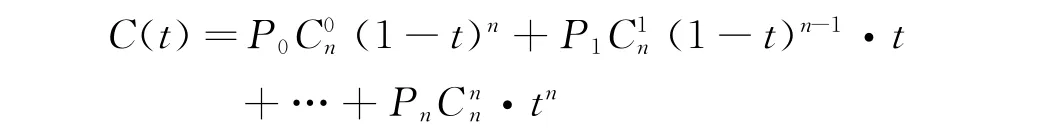

由此式我们可以得到下面关于Pi(i=0,1,…,n)的n +1个方程组构成的线性方程组由这组方程可解出Pi(i=0,1,…,n),这就是过Qi的Bezier曲线的特征多边形的顶点。
2.3 初始网格生成
初始网格是动网格生成的基准,因此初始网格需确保结构简单、鲁棒性强。本文选择机翼剖面翼型展向分布作为设计变量,机翼拓扑形状不发生改变且形变量小,为此采用索引简单易于程序编写的结构化网格,网格形状为拓扑结构简单正交性良好的O 型网格(图4)。本文使用商业软件Pointwise生成初始网格并将其导出成Plot3D格式文件,Plot3D格式是一种结构网格数据格式,它由NASA的CFD可视化软件推出,此格式将网格解析性的保存到文件中,且逻辑上清晰易于阅读,利于后续动网格编程。

图4 网格拓扑结构示意图Fig.4 Diagrams of grid topology
2.4 动网格生成
由于上述机翼优化过程中,网格形变量较小,且网格拓扑结构不发生变化,故采用简单可靠的线性插值实现网格的变形。沿机翼展向的任意截面翼型形状由控制截面依据B样条函数确定,因此机翼三维动网格过程退化为依次沿机翼展向不同位置的二维翼型截面动网格过程,截面数量为沿展向网格节点的数量。具体过程是:对任一截面以初始机翼网格Plot3D文件为基准,由B样条函数得到该截面新的壁面位置,将该壁面位置与初始壁面位置的位移平均分散到 O型网格的径向方向得到该截面新的网格。
设该截面 O型网格计算空间为ξ-η,ξi=const的为一条从截面翼型表面到远场的网格线。Δηj为该网格线上(ξi,ηj)和(ξi,ηj-1)的网格长度,设在截面翼型表面(ξi,η0)产生扰动量δi,则该网格线上新的网格坐标生成为

3 Pointwise自动化
网格Plot3D格式文件不能直接用于CFD流场计算,必须首先添加流场边界条件,对于本文O型网格机翼其边界条件有三个:壁面边界条件设为 wall、远场边界条件设为pressure-far-field、对称边界条件Symmetry。本文采用Pointwise软件给网格加入边界条件,由于机翼优化是一个自动优化过程,不能通过手动添加边界条件,需要编写一段Pointwise脚本语言Glyph2[13]实现边界条件设置过程的自动化。
需要指出的是由 Menu/Script/Begin Journaling可以录制出一段加边界条件的 Glyph2脚本草稿,为实现程序的简洁和脚本执行的可靠性,可将该草稿中冗余的语法删除,得到精炼的脚本程序。同时Pointwise设置边界条件的自动化过程可采用如下的批处理命令:
“$pointwise_home_path\\Pointwise\\Pointwise V16.04R1\\win32\\bin\\tclsh.exe”“$work_ home_path\\*.glf”.
4 Fluent自动化
Fluent是通用流场解算器,将Pointwise的CAE输出文件进行CFD仿真,得到对应变形后机翼的升力系数、阻力系数等。与Pointwise类似,由于优化过程需要流场计算自动化,不能通过手动设置解算条件。为实现商业软件Fluent的自动化,通常可以通过Menu/File/Write/Start Journal或者 Menu/File/Write/Stat Transcript两种方式录制一段脚本,在解算过程中加载该脚本即可自动执行计算。然而上述两种方式在设置过程中均要打开设置GUI界面,一方面运行效率较低,此外可能由于操作人员对Windows操作干预了 GUI使自动化过程中断。本文通过编写FLUENT 6.3 Text Command命令行,执行效率高且设置过程无需辅助 GUI,缺点是不能自动生成该命令行,初始设置需要尝试多次才能设置成功。为提高计算效率本文使用了分布式并行计算,Fluent自动化并行运行过程采用如下的批处理命令[14],其中host.txt为并行主机名称文件,*.jou为Text Command命令行文件。
“$Fluent_home_path\\Fluent.Inc\\ntbin\\ntx86\\fluent.exe”3d-t15-pnet-cnf=hosts.txt-i*.jou
5 iSIGHT集成
本文机翼优化是以控制截面翼型Hicks-Henne参数为优化变量,以功率因子最大为优化目标的单目标优化问题,其优化问题定义如式(8)。该优化是一个典型的基于软件集成的离散优化问题,常用iSIGHT集成软件实现以上各软件的集成优化。
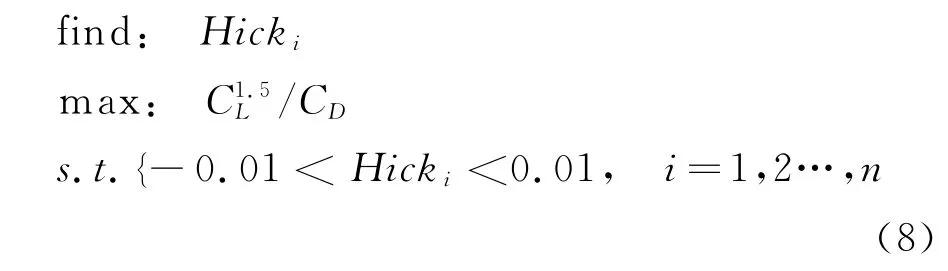
iSIGHT将数字技术、推理技术和设计探索技术有效融合,并把大量的需要人工完成的工作由软件实现自动化处理,从而代替工程设计者进行重复性的、易出错的数字处理和设计处理工作[15]。
优化集成过程如图5所示,其中Para Mesh是动网格模块、Pointwise是加边界条件模块、PreProcess 是Fluent并行计算前处理模块、GoFluent是流场解算模块、Power Factor是计算功率因子、Save History是后处理模块,将CFD计算结果归档保存并调用Tecplot脚本自动执行图形后处理、WingOptimal是优化器模块。
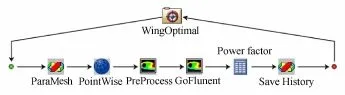
图5 优化集成过程Fig.5 Integration process
6 优化算例
本算例以翼型为 NACA 6409的大展弦比平直机翼为优化基准机翼,机翼弦长1m,展弦比为10,雷诺数为1.3692×106,马赫数为0.05877,网格量为1860236;Fluent求解器为Spalart-Allmaras,迭代步数8000。为减少设计变量规模,翼根处剖面不参与优化,只选取沿机翼展向1/3、2/3、1.0倍半展长作为三个控制截面,每个截面由12个 Hicks-Henne参数控制,故有36个设计变量。为便于叙述将沿机翼展现0.0倍半展长截面记为Original Airfoil,1/3倍半展长控制截面记为Airfoil 1,2/3倍半展长控制截面记为Airfoil 2,1.0倍半展长控制截面记为Airfoil 3。
设置Wing Optimal的优化方法选择为进化算法(Evolutionary Optimization Algorithm),最大进化代数(max Evolutions)为55。本算例总的优化时间约25天。图6所示为功率因子记录,图中可以看出在优化过程中功率因子总的趋势是增大的,且在第45次迭代达到最优。
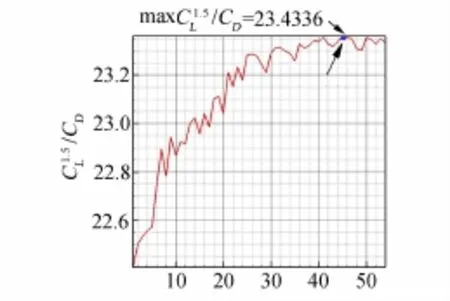
图6 优化历史曲线Fig.6 History of optimization process
表1所示是初始机翼和优化后机翼的升力系数、阻力系数、功率因子的对比,由表格可以看出优化后机翼较初始机翼功率因子提高4.44%,同时在保持阻力系数基本不变情况下,升力系数较初始机翼有所提高,该优化结论在确保高空长航时飞行器高功率因子需求的同时有较高的升力系数,是符合此类飞行器的气动性能需求的。
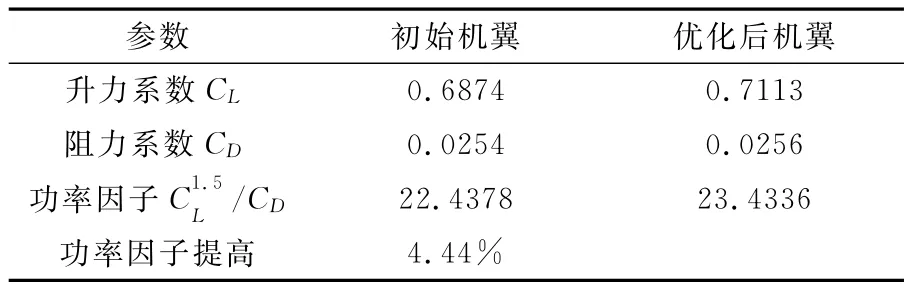
表1 优化结果对比Table 1 Comparison of initial and optimized wing
图7分别展示了三个机翼控制剖面同翼根剖面的压力系数对比,可以看出上述剖面翼型的上下表面压力差沿展向递减。图8(a)为优化后机翼流场的流线及三维效应示意图,图8(b)为优化后机翼表面压力分布图,图8(c)为三个控制剖面翼型同翼根剖面翼型几何对比,图中可以看出优化后机翼在靠近翼根处控制截面翼型弯度更大,由翼型理论可知有利于提高机翼整体的升力系数,而靠近翼尖处截面翼型弯度较小,其主要原因是为减小翼尖处上下翼面压差从而减小诱导阻力。为进一步准确描述该结论,本文以该机翼控制剖面处翼型弯度曲线方程沿弦向积分作为翼型弯度定量表述,并以翼根处截面为基准归一化,结果如表2所示,可以看出三个控制截面翼型弯度沿展向逐渐减小。

表2 控制面弯度对比Table 2 Camber curvature comparison of control profile
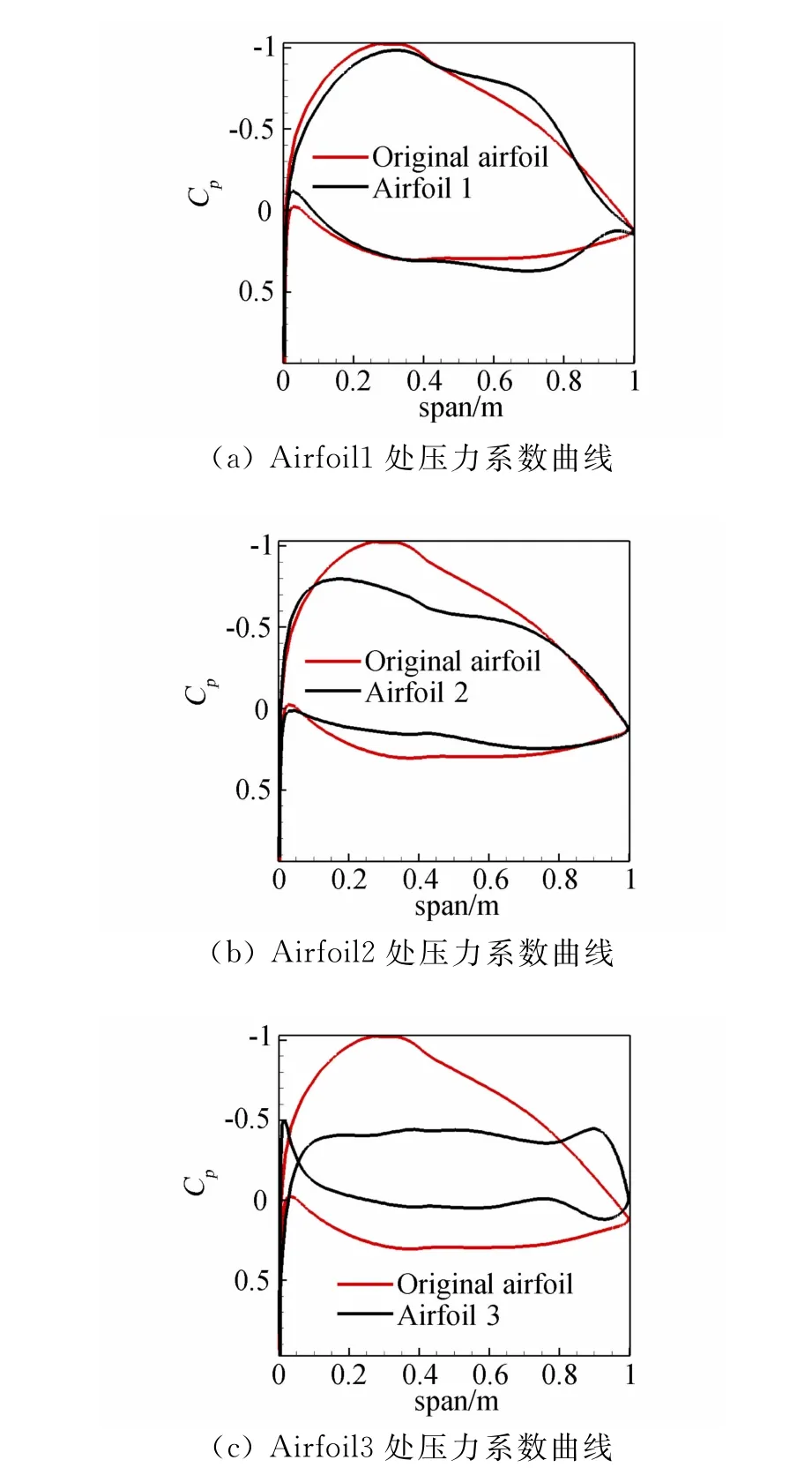
图7 控制面压力系数分布Fig.7 Pressure coefficient of wing control profile
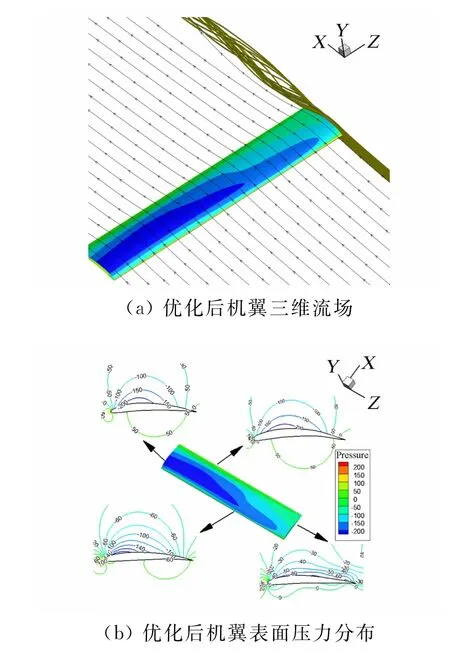
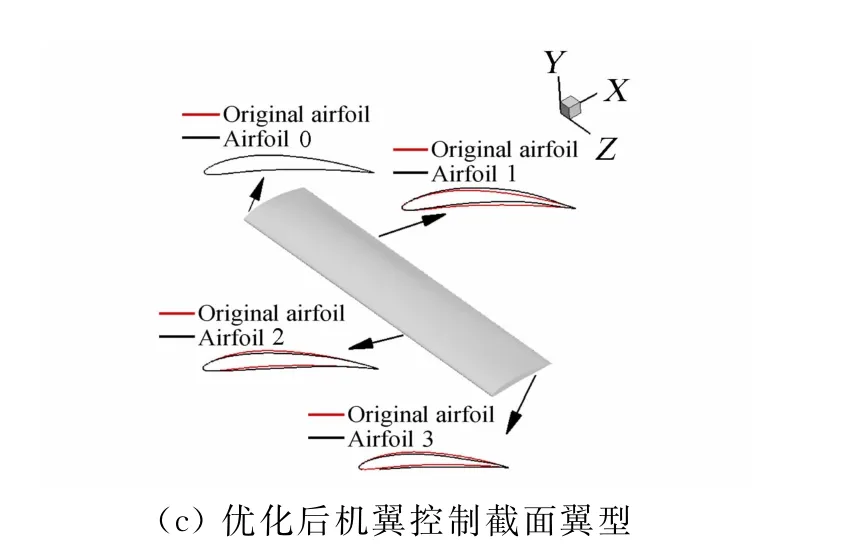
图8 优化后机翼流场分布Fig.8 Flow display of optimized wing
本文机翼优化主要针对该优化方案的可行性探索,由于计算条件有限,虽然采用了全局优化算法但考虑到计算代价太大,只执行了有限步数的优化,显然结果并未达到全局最优,但优化结果在一定程度上说明了高功率因子机翼的翼肋分布特征,对高空长航时飞行器设计具有一定的参考价值。
7 结 论
本文针对高空长航时飞行器大展弦比无后掠平直机翼优化,通过对机翼沿展向剖面翼型分布的优化,实现提高功率因子延长续航时间的目标。论文以标准的基于NACA系列翼型的平直机翼为基准,截取若干控制截面并对控制截面翼型参数化,首先对上述控制截面采用线性插值方法实现二维动网格,并依据B样条函数生成机翼三维动网格;通过对商业软件的二次开发实现Pointwise自动增加边界条件,和Fluent的并行流场解算以及Tecplot后处理,其中涉及自编程序和商业软件的数据流和工作流的交互,全部优化流程在iSIGHT平台下完成。优化算例表明该方法在提高大展弦比平直机翼的功率因子上是可行的,并在一定程度上反映了机翼剖面翼型沿展向分布的规律,该优化过程流程清晰,优化结果可信度高,是机翼优化的一个有效的方法。
[1] SUN M J,ZHAN H.Application of Kriging surrogate model for aerodynamic shape optimization of wing[J].ACTA Aerodynamica Sinica,2011,29(6):759-764.(in Chinese)孙美建,浩詹.Kriging模型在机翼气动外形优化中的应用[J].空气动力学学报,2011,29(6):759-764.
[2] FU H Y,ZHU Z Q,LIU H,et al.The optimization design of a simplified adaptive wing’s aerodynamic shape[J].ACTA Aerodynamica Sinica,2003,21(4):439-445.(in Chinese)付鸿雁,朱自强,刘航,等.简化自适应机翼的气动外形优化设计[J].空气动力学学报,2003,21(4):439-445.
[3] LI Y,ZHU Z Q,WANG X L,et al.Optimization design of wing's thickness and twist angle using Euler equations[J].Jour-nal of Beijing University of Aeronautics and Astronautics,2007,33(3):269-272.(in Chinese)李岩,朱自强,王晓璐,等.基于Euler方程的三维机翼厚度与扭角优化设计[J].北京航空航天大学学报,2007,33(3):269-272.
[4] WEN J H,ZHU Z Q,WU Z C,et al.Wing’s optimization design using serial and parallel computations based on N-S equations[J].Journal of Beijing University of Aeronautics and Astronautics,2008,34(2):127-130.(in Chinese)温建华,朱自强,吴宗成,等.基于N-S方程串并行计算的机翼优化设计[J].北京航空航天大学学报,2008,34(2):127-130.
[5] XIONG J T,QIAO Z D,HAN Z H.Aerodynamic optimization design of transonic airfoil and wing based on Navier-Stokes equation[J].ACTA Aerodynamica Sinica,2007,25(1):29-33.(in Chinese)熊俊涛,乔志德,韩忠华.基于 Navier-Stokes方程跨声速翼型和机翼气动优化设计[J].空气动力学学报,2007,25(1):29-33.
[6] TOAL D J J,KEANE A J.Efficient multipoint aerodynamic design optimization via co Kriging[J].Journal of Aircraft,2011,48(5):1685-1695.
[7] LEUNG T M,ZINGG D W.Aerodynamic shape optimization of wings using a parallel Newton-Krylov approach[J].AIAA Journal,2012,50(3):540-550.
[8] HICKS R,HENNE P A.Wing design by numerical optimization[A].AIAA Aircraft Sysetems&Technology Meeting[C].Seattle,Washington:1-7,1977.
[9] KULFAN B M.Universal parametric geometry representation method[J].Journal of Aircraft,2008,45(1):142-158.
[10]A R W D,B T R.Bezier-PARSEC:an optimized aerofoil parameterization for design[J].Advances in Engineering Software,2010:923-930.
[11]LIAO Y P,LIU L,LONG T.The research on some parameterized methods for airfoil[J].Journal of Projectiles,Rockets,Missiles and Guidance,2011,31(3):160-164.(in Chinese)廖炎平,刘莉,龙腾.几种翼型参数化方法研究[J].弹箭与制导学报,2011,31(3):160-164.
[12]SUN J G.Computer graphics[M].Beijing:Tsinghua University press,2010.(in Chinese)孙家广.计算机图形学[M].北京:清华大学出版社,2000.
[13]Pointwise Iuc.Pointwise User Manual[EB].2010.
[14]Fluent,Inc.FLUENT 6.3 Documentation[EB].2006.
[15]Dassault Systèmes Simulia,Corp.Isigth 5.0 design gateway online help[EB].2011.
Dynamic mesh based wing design optimization of HALE aircraft
ZHU Xiongfeng,GUO Zheng,HOU Zhongxi
(Collage of Aerospace Sciences and Engineering,National University of Defense Technology,Changsha 410073,China)
The commonly used method of wing design optimization is firstly analyzed in this paper.Design optimization method of the wing profile airfoil distribution along the wing span is put forward,according to the requirments of special aerodynamic performance and wing configuration features for a high altitude long endurance aircraft.Hicks-Henne parameterization method is improved against the drawback of unsmooth tailing edge,which is subsequently utilized for the construction of wing dynamic mesh.B-splines function based three-dimensional dynamic mesh generation method is proposed,as a substitute of commonly used linear interpolation based method.The customization and automation of data flow and work flow are realized by means of secondary development of commercial software Pointwise and Fluent,and all of the processes are integrated in iSIGHT platform.Finally,a wing optimization case for high altitude long endurance aircraft is studied using the aforementioned method,the optimization result shows that the endurance factor improves noticeably,indicates that the dynamic mesh based wing optimization method is an effective method.
HALE air vehicles;dynamic mesh;wing optimization;CFD;B-splines
TP391.9
Adoi:10.7638/kqdlxxb-2012.0144
0258-1825(2014)04-0468-06
2012-09-13;
2013-01-04
朱雄峰(1985-),男,博士研究生,研究方向:飞行器总体设计.E-mail:zhuxiongfeng@yeah.net
朱雄峰,郭正,侯中喜.基于动网格高空长航时机翼优化[J].空气动力学学报,2014,32(4):468-474.
10.7638/kqdlxxb-2012.0144. ZHU X F,GUO Z,HOU Z X.Dynamic mesh based wing design optimization of HALE aircraft[J].ACTA Aerodynamica Sinica,2014,32(4):468-474.

