N和硫属元素掺杂及共掺杂TiO2第一性原理计算

李昌盛， 任 君， 郭海燕， 彭 兴， 曹端林， 陈丽珍， 王建龙

（中北大学化工与环境学院，山西 太原 030051）

引 言

2001年，Asahi等［1］发现了 N掺杂锐钛矿型TiO2使其禁带宽度变窄、吸收峰红移，从而具有可见光的催化活性，并采用第一性原理的密度泛函理论（DFT）来研究掺杂TiO2的可见光催化原理。TiO2较广泛地应用于量子电子器件、光降解有机污染物等领域。但由于金红石的禁带宽度较宽（Eg＝3.0eV［2］），光吸收受局限，因此，为了提高催化活性，如何减小金红石的禁带宽度成为研究重点。

N掺杂在实验和理论计算中认为是一种最有用的方法而被广泛地研究。但由于N的2p轨道占据导带顶部［3］，致使N掺杂TiO2的效率并不高。因此，一些研究者对N和硫属元素进行了一些研究。Jenks W S等［4］指出，经Se掺杂TiO2之后，在可见光区域具有更快的降解速率，表现出更好的光催化性能。高洪宝等［5］运用第一性原理计算指出，N和S掺杂TiO2之后，S引入杂质带在价带和导带之间，从而电子从价带向导带的跃迁变得容易。时白成等［6］计算分析了阴离子掺杂TiO2的电子性质，认为，带间能级的出现使阴离子取代型S掺杂后吸收光谱发生红移。迄今为止，还没有人运用第一性原理对N和硫属元素掺杂金红石TiO2的性质进行研究。本文通过第一性原理从不同的角度对N和硫属元素掺杂与共掺杂金红石TiO2的性质进行了研究。

1 计算方法和模型

金红石TiO2结构属于四方晶系，空间群为P42／MNM。本文构造了2×2×2的超晶胞（如第67页图1所示），其晶体结构式为Ti16O32，分别构建N和硫属元素的单掺杂与共掺杂。在掺杂中，O原子被N和硫属元素所代替。

本计算采用基于密度泛函理论的Mede A的VASP［7－8］模块完成。用超软势来描述电子与离子之间的相互作用，电子间相互作用的交换关联能采用广义梯度近似（GGA）［9］中的 PBE［10］。在实意空间中进行计算，平面波截断选取为400eV，第一布里渊区间的积分计算使用 Monkhorst－Pack［11］方案，选择6×6×8的分格。U值选择为5。

图1 N和硫属元素共掺杂金红石TiO2超晶胞的掺杂物质的位置显示

本文分别对纯金红石TiO2进行N掺杂、硫属元素掺杂以及N和硫属元素共掺杂TiO2的晶型模型进行结构优化，收敛的精度是1×10－5eV，每个原子受力不大于0.02eV·（nm）－1。最后，计算得到晶体模型的构型、能带结构、取代能、态密度（DOS）、分态密度（PDOS）及bader电荷分析。参与计算的N和硫属元素的电子结构为N：1s22p3，O：2s22p4，Ti：3s23p63d24s2，S：2s22p63s23p4，Se：3s23p63d104s24p4，Te：3d104s24p64d105s25p4。

2 结果与讨论

2.1 掺杂后金红石TiO2的构型

首先，对纯金红石相TiO2晶胞进行结构优化，计算得到其晶格常数。由于本文采取的是广义梯度近似（GGA）中的PBE方案，该方法优化后的晶胞参数为a＝b＝0.462 7nm、c＝0.3019nm，与实验值a＝b＝0.459 4nm、c＝0.295 9nm及其他理论值［12］很好地相符合，说明该方法适合该计算。

在超晶胞的计算结果中，GGA－PBE方法计算的结果如表1中所示。计算的晶格常数和实验值［13］及其他理论值 相比都很接近。Sea＝0.933 3nmc＝0.5990nm）和Te（a＝0.937 4nm，c＝0.599 8nm）掺杂的超晶胞参数要大于纯的TiO2、N（0.922 7nm，0.596 8nm）和 S（0.918 8nm，0.591 8nm）。

表1 计算纯晶胞和N、S、Se、Te掺杂及（N／S）、（N／Se）、（N／Te）共掺杂的晶格参数a、b、c和V

经过优化后的晶体键长参数列于表2中。对于纯晶胞TiO2，键长是0.198 03nm。经过优化后，与N掺杂的晶胞相比，键长参数没有变化。然而，在共掺杂中，N掺杂的晶胞键长却有所增加。在单掺杂和共掺杂的体系中，与 Ti－N相比，Ti－X（X＝S，Se，Te）的键长较长。这 是因为，Se（0.160nm）、S（0.112nm）和Te（0.170nm）有着很大的原子半径，而N（0.080nm）和 O（0.060nm）却显得很小。从计算结果可看出，N和硫属元素的单掺杂和共掺杂都引起了晶格的畸变和体积的膨胀。

表2 经过结构优化之后单独掺杂和共掺杂二氧化钛的平均键长

2.2 取代能

为了研究N和硫属元素掺杂进金红石TiO2中的难度，进行了取代前、后取代能计算。取代能的计算按照公式（1）进行：

式中：E（codoped）代表N和硫属元素替换氧在金红石超晶胞中的整体能量；E（pure）代表的是纯金红石晶胞的能量；E（O）和E（doped）表示的是氧原子和N与硫属元素的单个原子的能量。

计算的取代能在表3中列出。从结果看，Te与其他元素替换氧原子的能量，其取代能是最大的。从单掺杂和共掺杂的体系取代能来看，共掺杂的取代能小些，这可能是原子半径大小的影响所致。从优化结构的结果中看出，在掺杂元素的周围，掺杂原子的半径决定了N和硫属元素在进行掺杂替换氧原子时需要克服很大的取代能。

表3 对于N、S、Se、Te掺杂和（N／S）、（N／Se）、（N／Te）共掺杂金红石二氧化钛的取代能和带隙能

2.3 掺杂后的金红石相TiO2的能带结构和态密度图

经结构优化后计算的能带结构如图2（a）所示。对于纯金红石TiO2来说，其得到的能带宽度是2.80eV，尽管与实验值3.0eV还有一点差距，但已很接近，证明该方法适合该体系的计算。

基于以上纯金红石相TiO2的计算结果，我们计算了N和硫属元素通过单掺杂和共掺杂的能带结构，并与纯金红石相TiO2进行了比较。图2中都是将费米能级定位能量零点，由于杂质的引入，电子最高占据能级发生了很大的变化，禁带中的费米能级与价带以及导带的相应位置也发生了变化。当掺杂N时［如图2（b）所示］，在费米能级周围，也就是价带顶部，形成了一条杂质能级，致使N掺杂的带隙宽度减小到2.62eV，杂质能带跨越费米能级，电子在该能带是未填满状态。由于导带与价带的禁带宽度变小，致使与价带顶部的距离变得很小，使其变成了受主能级，从而使电子从导带向价带的跃迁变得更容易，更有利于光生电子和空穴的迁移，增强了光催化性能。

对于S掺杂［如图2（c）所示］，TiO2的导带边和费米能级的距离有所减小，其带隙减小到2.48eV但在导带底部出现了一条新的杂质能级，致使电子能级向导带底部移动。

对于Se和 Te掺杂［图2（d）和（e）所示］，费米能级发生了很明显的上移，随之在价带顶部出现了一条新的杂质能级，使其在价带顶部和费米能级发生杂化，杂质能级并未能跨越过费米能级，电子在该能级上处于满填充状态。费米能级在Te的掺杂中很明显地向上移动，在Se的掺杂中则是相对上移趋势较小。

图2的（f）、（g）和（h）是（N／S）、（N／Se）和（N／Te）的共掺杂能带图。掺杂后的金红石相TiO2，费米能级有着明显的上移，其带隙都减小到2.46、2.37和2.42eV，致使费米能级与导带底部相接近，使其空穴和电子的跃迁更加容易。相比于元素的单掺杂能带图来说，在费米能级中间出现了2条杂质能级，靠近导带底部的一条杂质能级距离费米能级较近，而另外一条杂质能级距离费米能级较远，距离价带顶部较近。（N／Se）与（N／S）的情况相似，一条在导带底部，另一条在价带顶部。但（N／Te）却不同，导带底部和价带顶部的2条杂质能级互相靠近，致使杂质的能级趋于结合化。根据公式λ＝hc／E对（N／S）、（N／Se）和（N／Te）进行计算，结果分别为504、523和512nm，已经进入了可见光区域（400 nm～760nm），提高了TiO2对可见光的响应。由于费米能级处于杂质能带处，杂质能带中的电子处于半满状态，电子可能发生从价带到杂质能级或者从杂质能级到导带的跃迁，使（NS NSe 的空穴和电子的结合速率变得缓慢，电子跃迁容易，从而掺杂后的TiO2能提高可见光的利用率。

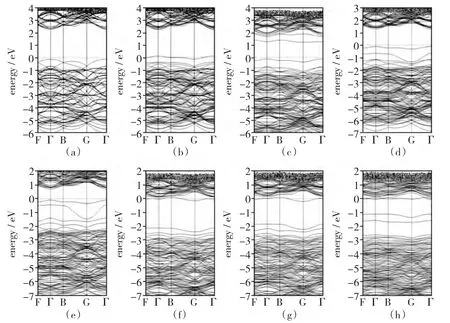
图2 计算（a）纯金红石，N、S、Se、Te掺杂二氧化钛和（N／S）、（N／Se）、（N／Te）共掺杂二氧化钛的能带结构

为了进一步研究经过单掺杂和共掺杂的这些杂质能级的构成，对掺杂前、后的电子态密度图进行研究。纯TiO2、N和硫属元素单掺杂与共掺杂TiO2的总态密度图如图3（a）、（b）、（c）所示。未掺杂的纯态TiO2在费米能级附近的导带和价带主要是由Ti原子的3d轨道和O原子的2p轨道所组成。其中，价带部分主要是O原子2p电子的贡献，而导带部分主要是Ti原子3d电子的贡献。相对于纯TiO2而言，N和硫属元素的掺杂，使TiO2的价带带边能级、导带带边能级以及带隙宽度都有不程度的变化。其中，N掺杂在费米能级附近形成了杂质能级，对导带只有很小的影响；硫属元素掺杂后使费米能级向导带移动，同时在费米能级下形成了杂质能级，杂质能级被电子占据。Te的带隙中有2个杂质能级带，但相对于价带顶部而言，仍有一定的距离。

图3（d）、（e）、（f）是 N 和硫属元素的单掺杂与共掺杂的分态密度图曲线。如图所示，原子的掺杂对导带有一定的影响，费米能级作为能量的零点。因为杂质能级带的引入，致使费米能级作为电子占据的最高占据激发态发生上移，在价带顶部形成了杂质能级，有电子态密度的贡献，导带与费米能级的距离减小。在价带中，主要是O原子的2p轨道占据p电子的态密度的贡献，致使其值发生变化。在N和S共掺杂态密度图中，N原子的2p轨道和S原子的3p轨道组成在价带中，而S原子3p轨道贡献较大一些，与前面的能带分析相一致。在N和Se以及Te的共掺杂中，N原子2p轨道和Se原子4p轨道及Te原子5p轨道互相杂化组成在价带顶部，形成杂质能级。其中，Se原子4p轨道和Te原子5p轨道主要占据价带，对其贡献大些，使电子从价带向导带的跃迁变得容易。在共掺杂的体系中，N、S的共掺杂使得费米能级发生上移，而在价带顶部附近出现了杂质能级，N和S替换了O原子位置，使其成为浅受主能级，从而在TiO2中形成部分空穴。所以，N和S共掺杂在TiO2中起到了p型掺杂剂的作用。在N和Se的共掺杂中，导带底部和价带顶部各出现一条杂质能级，N和Se取代O原子，使得带隙能级减小，费米能级上移，电子从导带跃迁到价带所需能量减小，在导带底部和价带顶部各形成一个空穴，使其变成深受主能级。在N和Te的共掺杂中，带隙能级减小，但N和Te原子替换了O原子位置之后，在禁带中间出现了2个空穴，使得电子从价带跃迁时需要的能量增多，经过掺杂后，起到了p型掺杂剂的作用，使得电子可以很容易地从价带向导带进行跃迁，而且需要很少的光电子能量就可完成，可以作为电子从价带跃迁到杂质能级上，再很容易地吸收光电子能量后直接跃迁至导带上。这种情况下，金红石相TiO2对可见光的吸收有很大的提高。

图3 计算纯晶胞和掺杂二氧化钛的总态密度图和分态密度图

为了分析电子在金红石相中的转移，我们进行了bader电荷［15］的分析，计算的结果如表4所示。其中，对于单掺杂的N、S、Se和Te，包含的电子数是6.18、6.72、6.48和5.95。对于共掺杂，（N／S）为6.19（N）和6.72（S），（N／Se）为6.34（N）和6.18（Se），（N／Te）为6.19（N）和 5.93（Te）。结果指出，在（N／S）和（N／Te）中没有电子转移，（N／Se）中有少量的电子转移。

表4 N、S、Se、Te掺杂和（N／S）、（N／Se）、（N／Te）共掺杂金红石二氧化钛中计算的bader电荷分析

3 结论

本文运用第一性原理计算进行了纯金红石相TiO2经N和硫属元素的单掺杂和共掺杂后优化的晶体模型的构型、能带结构、取代能、态密度（DOS）、分态密度（PDOS）及bader电荷分析。

1）经过优化的晶体构型，由于Se（0.160nm），S（0.112nm）和 Te（0.170nm）有着很大的原子半径，N和硫属元素的单掺杂和共掺杂都引起了晶格的畸变和体积的膨胀。

2）相比较于其他元素而言，Te更难掺杂进TiO2中是由于较大的取代能。

3）共掺杂后的TiO2的能带中出现了2条杂质能级，靠近导带底部的一条杂质能级和靠近价带顶部的杂质能级致使带隙减小，获得更好的光催化效果。杂质能级主要是由N原子的2p轨道和S原子的3p轨道、Se原子的4p轨道以及Te原子的5p轨道相互杂化在一起组成。其中，S原子的3p轨道、Se原子的4p轨道以及Te原子的5p轨道在价带的贡献较大一些。这样掺杂可以提高金红石相TiO2的可见光吸收性，从而减少电子从价带跃迁到导带所需的能量。

4）Bader电荷分析可知，在（N／S）和（N／Se）中无电子转移，而在（N／Te）中有少量的电子转移。

［1］Asahi R，Morikawa T，Ohwaki T，et al.Visible－light photocatalysis in nitrogen－doped titanium oxides［J］.Science，2001，293：269－271.

［2］Tang H，Levy F，Berger H，et al.Urbach tail of anatase TiO2［J］.Phys Rev B，1995，52：7771－7774.

［3］Irie H，Watanabe Y，Hashimoto K J.Nitrogen－concentration dependence on photocatalytic activity of TiO2－XNXpowders［J］.Phys Chem B，2003，107：5483－5486.

［4］Jenks W S，Howk R S，Rockafellow E M，et al.Selenium－modified TiO2and its impact on photocatalysis［J］.Langmuir，2010，26：19052－19059.

［5］Gao H T，Liu Y Y，Ding C H，et al.Synthesis，characterization and theoretical study of N，S－codoped nano－TiO2with photocatalytic activities［J］.Int J Min Met Mater，2011，18：606－615.

［6］Shi B C，Liu Yong，Song C L，et al.First－priciples invetigation of the band structure of S－doped TiO2［J］.Rare Metal Materials and Engineering，2008，37（5）：638－640.

［7］Hafner Kresse G.Ab initio molecular dynamics for open－shell transition metals［J］.Phys Rev B，1993，48：13115－13118.

［8］Hafner，Kresse G.Ab initio molecular－dynamics simulation of the liquid－metal－amorphous－semiconductor transition in germanium［J］.Phys Rev B，1994，49：14251－14269.

［9］Perdew J P，Wang Y.Accurate and simple analytic representation of the electron－gas correlation energy［J］.Phys Rev B，1992，45：13244－13249.

［10］Perdew J P，Burke K，Ernzerhof M.Generalized gradient approximation made simple［J］.Phys Rev Lett，1996，77：3865－3868.

［11］Monkhorst H J，Pack J D.Special points for brillouinzone integrations［J］.Phys Rev B，1976，13：5188－5192.

［12］Thompsom S J，Lewis S P.Revisiting the（110）surface structure of TiO2：a theoretical analysis［J］.Phys Rev B，2006，73：073403－073407.

［13］Burdett J K，Hughbanks T，Miller G J，et al.Structural－electronic relationships in inorganic solids：powder neutron diffraction studies of the retile and anatase polymorphs of titanium dioxide at 15and 295K［J］.J Am Chem Soc，1987，109：3639－3646.

［14］Long R，English N.Energetic and electronic properties of P doping at the rutile TiO2（110）surface from first principles［J］.J Phys Chem C，2009，113：9423－9430.

［15］Tang W，Sanville E，Henkelman G.A grid－based bader analysis algorithm without lattice bias［J］.J Phys Condens Matter，2009，21：084204－084211.