航运下行期的航线配船和航次设计优化

邵俊岗，薛颖霞

(上海海事大学科学研究院，上海 201306)

0 引言

后金融危机时代，全球经济持续低迷，加之欧债危机不断深化、市场融资环境日益恶化和船舶供给压力过大等不利因素的影响，全球航运市场长期在底部振荡徘徊.航运企业由于难以吸纳充足的货源，面临严重的运力过剩，大量新船的陆续交付无疑也使各航运公司的处境更为艰难.合理的航线配船和航次设计可以帮助航运企业充分利用现有的船舶，以最少的投入或消耗换取最大的产出或效益，对航运公司具有重要的意义.

关于航线配船问题，国内外众多学者已经进行广泛的研究，并提出多种解决方案.RONEN［1］根据货运状况提出优化给定航线的航线配船方案.谢新连在文献［2］中建立船队规划线性模型，其目标函数为船队营运和造船总费用最小化，并在文献［3］中对船舶调度、船队规划等问题用线性规划、非线性规划、动态规划等多种方法进行求解.苏绍娟［4］建立不确定动态船队规划的数学模型.杨秋平等［5］建立考虑船舶航速的船队规划非线性数学模型.BRONMO等［6］构造一个航线配船的主问题以及一个基于该主问题的子问题.陈颖［7］尝试将遗传算法与模拟退火算法相结合，引入班轮配船问题.林珈伊等［8］在线性规划的航线配船模型基础上，建立受船闸时间阻抗变动影响的航线非线性配船模型.目前，国内外关于航运周期的研究还相对较少，STOPFORD［9］将航运市场周期分为波谷期、恢复期、高峰期和下滑期等4个阶段，并详细阐述各阶段的特征以及一些影响因素.

上述文献尝试用各种方法解决班轮的配船问题，但是并未将航运业的周期性特征考虑在内.在航运下行期，集装箱船舶的装载率普遍下降，而目前大部分关于航线配船的研究并未考虑航运周期性对装载率的影响.另外，传统模型对同一航线上同一船型的集装箱船舶均设置同样的航次，与现实中班轮公司所采取的措施不符，也使班轮公司的收益难以实现最大化.为弥补传统航线配船的不足，本文根据航运下行期的特点，建立关于航线配船和航次设计的整数规划模型，并尝试用MATLAB编程的遗传算法对该模型进行求解.

1 航线配船和航次设计模型建立

1.1 问题描述以及模型假设

假设某公司现有m种载质量的集装箱班轮运营在n条航线上，在装货港一次装载货出发，航行到卸货港之后，一次性卸完货物.研究阶段处于航运下行期，现对该公司的航线配船和班轮航次进行设计，以较低的运营成本完成运输任务，争取获得最大的收益.

为便于研究，本文以1年为规划期，并假设:①规划期内该公司没有新的集装箱班轮交付;②规划期内该公司没有集装箱班轮退役;③所预测的运量较为准确，且所有运量较为均匀地发生在1年的各个时期;④采取规划期内的平均运价.

1.2 符号说明

假设:某船公司现有的船舶种类集合V={i|i=1，2，…，m};其所经营的航线集合 R={j|j=1，2，…，n};L为1年内航线配船方案的总利润;船型i的装载量为Wi，数量为Si;Hij为i型船在航线j上可以选择的航次种类数，例如H12=4为船型1的船舶在航线2上可以选择4种不同的航次;Pj1为正向航线j上运输1 TEU的收入，定义为正向航线j上承运1 TEU的运费率;Pj2为反向航线j上运输1 TEU的收入，定义为反向航线j上承运1 TEU的运费率;Qj1为正向航线j上当年预测的运量;Qj2为反向航线j上当年预测的运量;Ei为i型船当年的闲置费用(被封存的船虽然不再有运营费，但是仍然存在保养费、看管人员工资等费用);Zi为闲置的i型船的数量;Rj1为正向航线j上最大平均装载率;Rj2为反向航线j上最大平均装载率;tijh为i型船在航线j上选择以第h种航次运营时的年往返航次，例如t111=3为船型为1的船在航线1上以第1种航次运营时的年往返航次为3;Cijh为i型船在航线j上每年完成tijh个往返航次时每个航次的航次成本，包括燃料费、港务费和航次费用等;决策变量xijh为被分配在航线j上每年完成tijh个往返航次的i型船的数量.

1.3 模型构建与解释

1.3.1 模型构建

在航运下行期，由于货运需求下降，大多数航线的装载率普遍下降，班轮公司多采取降低航速、减少年航次等措施降低运营成本，这时在同一航线上同一型号的船舶每年可能会完成不同的航次.本文所建立的模型加入对装载率的考虑，并设定在同一航线上同一船型可以选择不同的航次(此时单位航次成本因航速的变化而发生变化)，更符合航运下行期的特点.其目标函数为

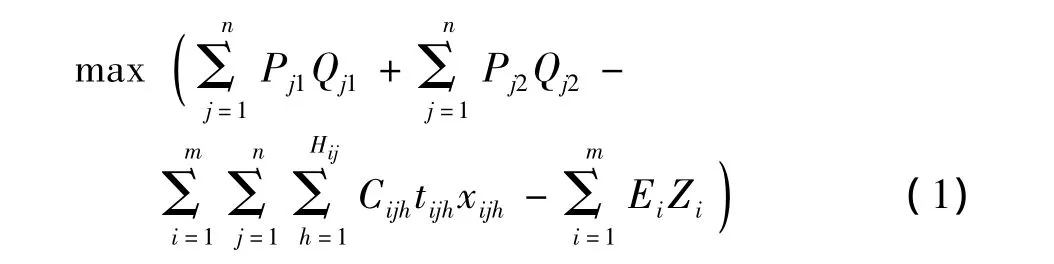
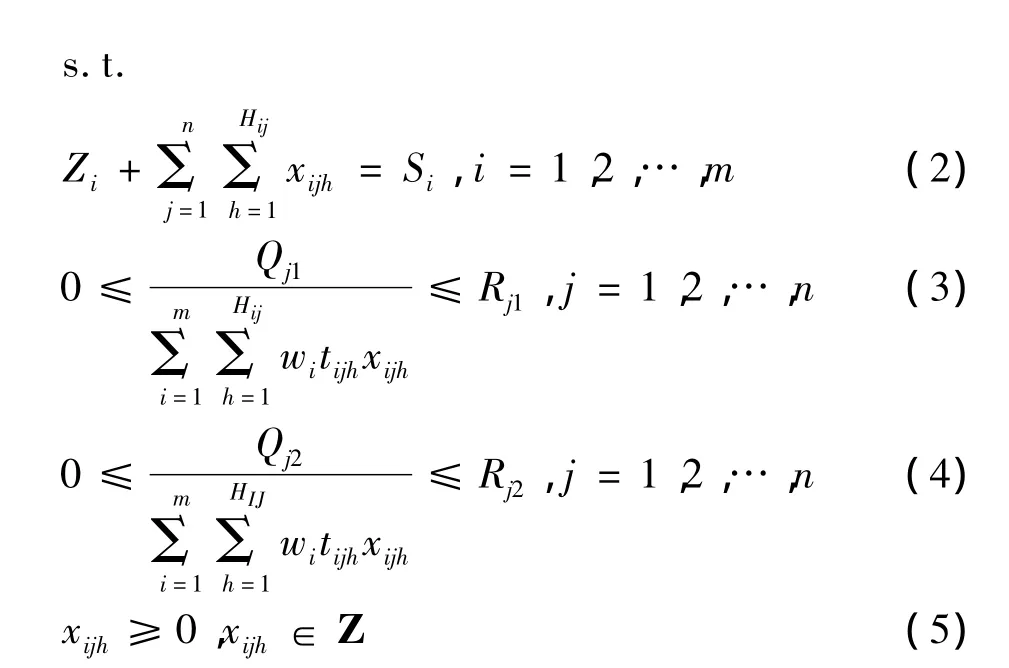
1.3.2 模型解释

该模型对集装箱正向运输和反向运输采用不同的运价和运量，这样的处理更符合实际.式(1)表示在规划期内航线配船方案的总利润最大.式(2)是对船舶数量的约束，即所有航线上某种船型船舶的总数与该船型闲置船舶的数量之和必须等于该船型船舶的总数.式(3)和(4)是对船舶最大平均装载率的约束，即在航运低迷期适度减少航次可以在一定程度上提高船舶的平均装载率，但是船舶的装载率仍会保持在一定的范围内，过高的平均装载率不符合航运下行期的实际情况.式(5)是对决策变量的非负性以及整数约束.

2 算法实现

2.1 遗传算法原理

遗传算法(Genetic Algorithm，GA)是模拟达尔文适者生存、优胜劣汰的生物进化论的自然选择原理和遗传学的生物进化过程而演化出的搜索最优解的方法，是一种新型全局优化搜索算法，由美国密歇根大学的HOLLAND教授于1975年首先提出.GA能有效解决许多由经典数学方法无法解决的复杂的、大规模的难题.GA一般流程见图1.

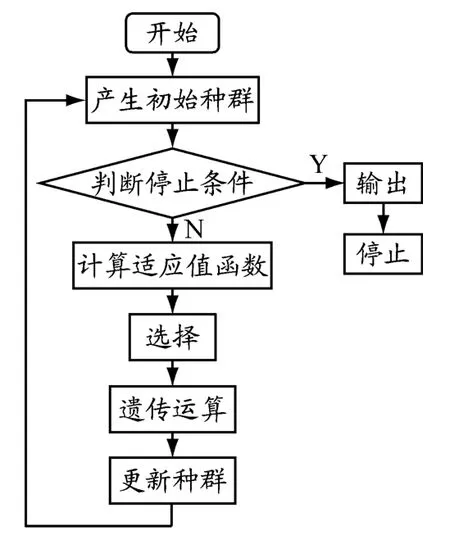
图1 GA流程图

2.2 遗传算法设计

2.2.1 染色体设计

由于航线配船问题所涉及的因素较多(包括航线、航次、船舶数量等)，较为复杂，本文采用浮点数编码方式代替传统的二进制编码.将1年内在某条航线上以某种年往返航次进行运营的某种船型的船舶总数作为一个基因位，见图2.例如:第1个基因位代表在航线1上以第1种年往返航次运营的船型1的船舶数量，第2个基因位代表在航线1上以第2种年往返航次运营的船型1的船舶数量，其余基因位的含义依此类推.

图2 染色体结构示意

为便于对原模型进行GA编程，需要对决策变量的表示方式进行一定的变化，现以船型1的分配为例进行说明.原模型中的x111，x112和x113(在航线1上分别以第1，2，3种年往返航次进行运营的第1种船舶的数量)在编程中分别用x1，x2和x3表示，其他船型船舶数量变化方式依此类推.

2.2.2 产生初始种群

为保持种群的多样性和解的质量，采用随机方式产生初始种群.一般而言，种群规模通常为个体编码长度的一个线性倍数，通常在n与2n之间.本文建议在试验中调整种群数量以便取得较好的计算效果.

2.2.3 适应度函数

采用MATLAB对遗传算法编程，适应度函数为f(x)=cmax－L，其中cmax是根据多次试验的收敛结果确定的.

2.2.4 选择操作

选择过程是根据个体的适应度从种群中选择个体复制到中间代，直至达到种群规模的过程.选择目的是将最优个体直接保留到下一代中，使种群得到进化.GA中有多种选择操作方法，本文采用最常用的轮盘赌方法进行选择操作.

2.2.5 交叉操作

交叉过程是利用随机概率将种群各个体之间的信息进行相互交换从而产生新染色体的过程.交叉的目的是增加种群的多样性.交叉运算是GA不同于其他进化算法的重要特征，它在GA中起关键作用，是产生新个体的主要方法.交叉操作的种类很多，本文采用两点交叉的方式，随机将中间代的染色体两两配对.

2.2.6 变异操作

变异运算是GA中产生新个体的辅助方法，它能决定GA的局部搜索能力，同时能保持种群的多样性.交叉运算和变异运算在GA中相互配合，共同完成对搜索空间的全局搜索和局部搜索.本文采用单点变异的方法进行新的航线配船选择，得到新的染色体.

2.2.7 终止准则

采用最大代终止法，即计算在迭代代数达到所给定的最大遗传代数时停止，输出所得到的最优解.

3 算例验证与分析

为验证所建模型的有效性，用GA对一个算例进行求解.某公司拥有3种装载能力的集装箱船，分别为1686 TEU，1250 TEU，850 TEU，共有4 条集装箱航线，船舶参数及其年闲置费用见表1.根据所预测的运量需求(见表2)，将不同船型的船舶配置在这4条航线上以求获得最大的经济效益.因为可获得数据有限，对于船型相同、在同一航线上年航次不同的船舶采用同样的单位航次成本.各船型在各航线上的单位航次成本，最大、最小年航次和最大平均装载率分别见表3～5.各航线集装箱运价见表6.

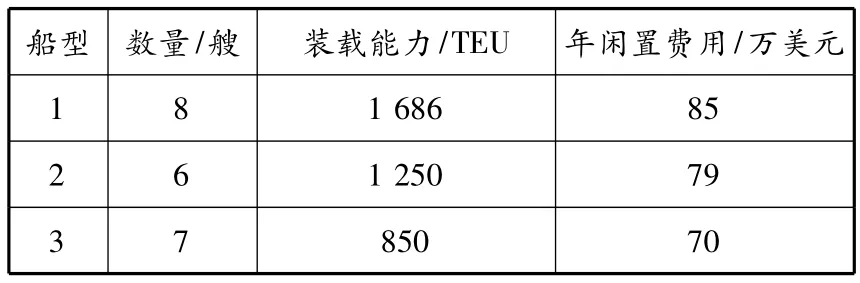
表1 船舶参数及其年闲置费用

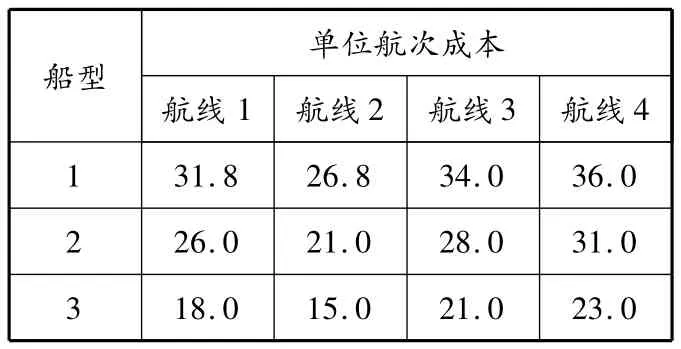
表3 各船型在各航线上的单位航次成本 万美元

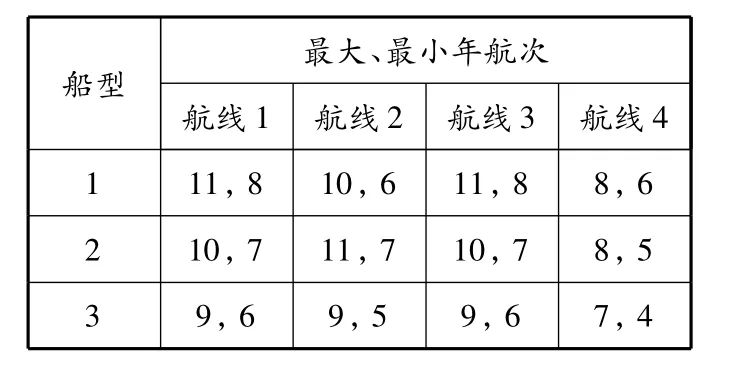
表4 各船型在各航线上的最大、最小年航次 次

经过反复试验，在设定该GA的种群规模为72，最大遗传代数为100，交叉概率为0.7500，变异概率为0.0078时效果较好.该GA可在遗传代数为50左右时给出最优解，所得到的最大利润稳定在1.56亿美元左右.最终用GA所得到的航线配船的最优解见表7，其总利润为15703.20万美元.

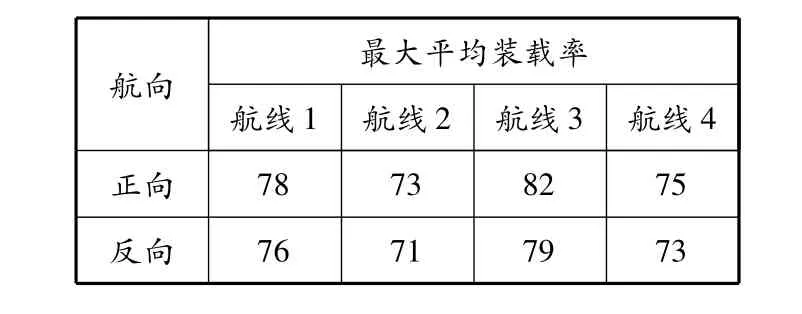
表5 各航线最大平均装载率 %

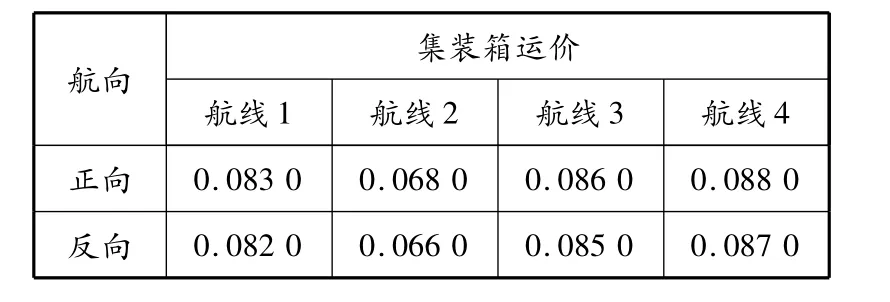
表6 各航线集装箱运价 万美元/TEU

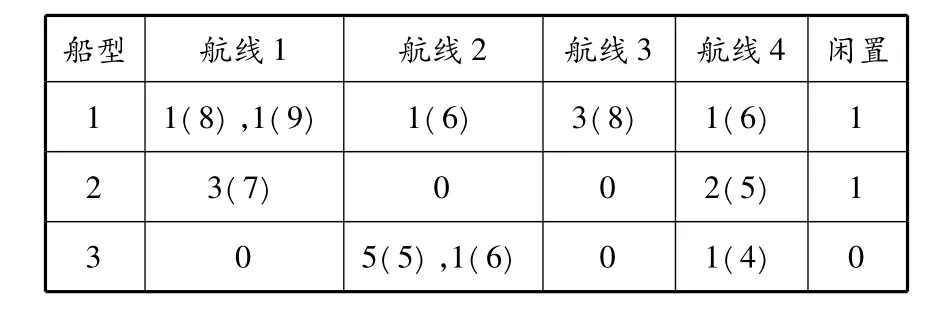
表7 航线配船GA最优解

表7中括号里的数字表示航次，括号前的数字表示在该航线上以括号中的年往返航次运营的该船型船舶的数量.如“1(8)，1(9)”表示航线1上应分配2艘第1种型号的船舶，其中1艘每年运营8个航次，另外1艘每年运营9个航次.最后一列代表各船型闲置船舶的数量.

运用 LINGO求解该模型，得到的最优解是15728.20万美元，GA所得到的最大利润与之仅相差0.159%左右，这证明本文所设计的算法能较好地收敛到近似最优解，且耗时更短.由以上结果可以看出，通过合理优化班轮公司的航线配船和航次设计方案可以实现收益的最大化.

4 结束语

在现有航线配船模型的基础上，结合现阶段航运下行期的特点，建立混合整数规划模型，对航线配船和班轮航次进行优化设计，并运用GA对该模型进行求解，最后将其结果与LINGO计算结果进行比较，验证该模型的可行性和该算法的有效性.因此，本文对班轮公司根据航运下行期的特点设计航线配船方案具有重要的参考意义.

［1］RONEN D.Cargo ships routing and scheduling:survey of models and problems［J］.Eur J Operational Res，1983，78(5):46-49.

［2］谢新连.船队规划的线性模型研究与应用［J］.中国造船，1989(3):59-66.

［3］谢新连.船舶调度与船队规划方法［M］.北京:人民交通出版社，1997:75-86.

［4］苏绍娟.不确定动态船队规划的数学模型研究［J］.中国航海，2008，31(2):158-161.

［5］杨秋平，谢新连，裴光石.考虑船舶航速的船队规划非线性模型［J］.华南理工大学学报:自然科学版，2011，39(10):119-126.

［6］BRONMO G，NYGREEN B，LYSGAARD J.Column generation approaches to ship scheduling with flexible cargo sizes［J］.Eur J Operational Res，2010，200(1):139-150.

［7］陈颖.基于混合遗传-模拟退火算法的集装箱班轮配船模型［J］.集装箱化，2011，32(7):18-20.

［8］林珈伊，陶桂兰.船闸阻抗影响下的内河航线非线性配船模型［J］.上海海事大学学报，2012，33(2):14-17.

［9］STOPFORD M.Maritime economics［M］.3rd ed.Taylor＆ Francis，2008:93-103.