画图解重叠问题

◎浙江 杨国义

重叠问题是指两个(或几个)数量之间存在着重叠(即交叉)关系的问题。解重叠问题一般采用图示法，就是根据题意画出示意图，再借助图形分析解答。

【例1】三(1)班共有19人参加书法和绘画兴趣小组，其中参加书法组的有12人，参加绘画组的有9人，两组都参加的有多少人？

【分析与解】这是一个重叠问题，可以通过画图来帮助解题。根据题意画出图1，其中整个图形表示一共参加的19人，A圈表示参加书法组的人数，B圈表示参加绘画组的人数，两圈的重叠部分表示两组都参加的人数。

从图中可以看出，涂色部分表示只参加书法组，不参加绘画组的人数。很明显，整个图形的人数减去B圈的人数等于涂色部分的人数，也就是只参加书法组的人数，所以，只参加书法组的有19－9=10(人)。同时，因为A圈减去涂色部分就是中间的重叠部分，即两组都参加的人数，因为A圈是12人，所以两组都参加的学生有12－10=2(人)。

也可以这样想：如果把A圈与B圈的人数加起来，重叠部分的人数就算了两次，也就是A圈与B圈的和比整个图形多了一个重叠部分，所以重叠部分，即两组都参加的人数是12+9－19=2(人)。

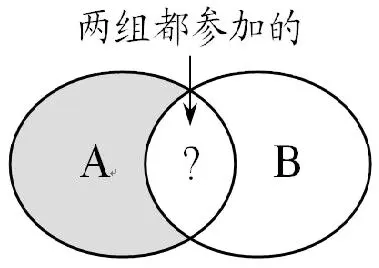
图1

【例2】三(2)班有44人，喜欢跳绳的有28人，喜欢踢毽子的有17人，这两项活动都喜欢的有9人。请问：

(1)只喜欢跳绳的有多少人？

(2)喜欢跳绳和踢毽子的一共有多少人？

(3)这两项活动都不喜欢的有多少人？

【分析与解】这道题也可以通过画图来帮助解答。根据题意画出图2，其中长方形表示全班人数，A圈表示喜欢跳绳的人数，B圈表示喜欢踢毽子的人数，两圈的重叠部分表示两项活动都喜欢的人数，涂色部分表示两项活动都不喜欢的人数。

(1)从图中可以看出，只喜欢跳绳的人数，就是A圈的人数减去重叠部分的人数，所以只喜欢跳绳的有28－9=19(人)。

想一想：只喜欢踢毽子的有多少人？

(2)从图中可以看出，喜欢跳绳和踢毽子的总人数，就是图中空白部分所表示的人数，即只喜欢跳绳的19人加B圈的人数，所以一共有19+17=36(人)。想一想：还可以怎样算？

(3)因为喜欢跳绳、踢毽子的一共有36人，全班共有44人，所以两项活动都不喜欢的学生有44－36=8(人)。

【小试身手】三(3)班同学喜欢打乒乓球的有18人，喜欢打羽毛球的有15人，两种活动都喜欢的有5人，都不喜欢的有14人。

(1)喜欢打乒乓球、羽毛球的共有多少人？

(2)三(3)班一共有多少人？

图2