利用线性规划进行金工实习中心资源优化配置的探讨

◆叶钟辉

作者：叶钟辉，南京工业大学实习教师（210009）。

1 引言

随着高校的不断扩招，高校学生人数不断增加。紧随而来的是各高校在师资、设备、仪器等软、硬件方面投入也在不断增长，如何能在有限的资源投入情况下，尽可能地合理分配好资源，使其尽可能地发挥其作用，成为现在急需解决的一个问题。

2 研究内容

学生参加金工实习是大学高等教育的一个重要组成部分，通过各个工种的实习，一个学生最终完成金工实习的学业。通常，不同的机床、设备所能承担的实习学生数是不相同的。例如，一台车床最多能承担1名学生参加实习，而一台铣床却能承担4名学生参加实习。另外，由于学生在实习过程中要分成多个小组，在不同的实习工种中同时进行，不同小组的学生虽然都要实习同样的所有工种，但他们实习的顺序不同，这就如同产品生产中工艺不同一样。因此，不同小组的学生参加实习的实习流程是不一样的。每一批学生实习，都是由不同的几个实习流程组成。本文研究的，就是通过资源优化，使得有限的投入在金工实习中发挥最大作用，尽可能地多承担一些学生参加金工实习。

3 模型的提出

为完成学生的实习任务，金工实习各实习工种内需配置各种资源，包括人力资源——实习教师，物力资源——机床设备、各种材料、机物料等。实习中心应如何配置这些资源，才能使金工实习中心以尽可能少的资源满足每年实习学生的需要？原有的资源是否能够满足？需要添置多少资源？哪些资源？这些问题都要通过线性规划来解决。

对于资源优化配置，目前有许多种方法，而线性规划是应用最为广泛的一种系统优化的方法。下面要建立线性规划的数学模型[1-3]，首先做如下假设：

金工实习中心实习过程中共经历i个工种，各个工种内每批学生所需要的实习教师成本为a1,a2,…,ai，各个工种所配备机床设备的成本为b1,b2,…,bi，材料、机物料消耗的成本为c1,c2,…,ci，各工种每批所能承担的学生数为n1,n2,…,ni，各工种承担学生的批次为x1,x2,…,xi，各个工种实习成本为Mi=ai+bi+ci，所承担的实习学生总数为Zmax=x1n1+x2n2+…+xini。将Zmax作为目标函数，求其最大值。金工实习中心全年的实习学生总数为Q，Q≤Z成为约束条件之一，各工种每年学生成本的投入也是约束条件之一。考虑到x1,x2,…,xm的实际意义，要求x1,x2,…,x8为整数。

综合以上的条件构成如下线性规划：

目标函数：Zmax=x1n1+x2n2+…+xini

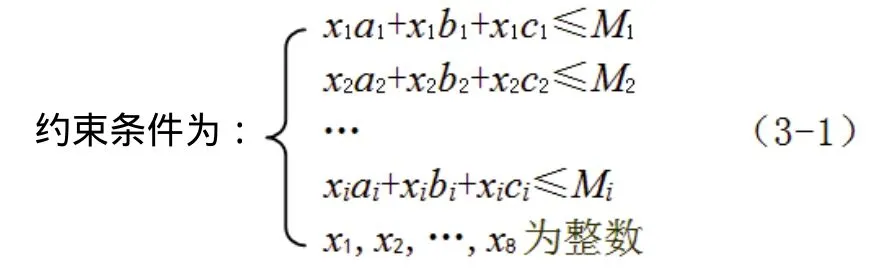
4 算法实例

南京工业大学金工实习中心资源数据 南京工业大学金工实习中心是南京工业大学内为学生提供实习培训的部门。学生参加金工实习，需经历车工、钳工、铸工、焊工、普铣磨、数控铣、数控车、线切割等八个工种的实习。

1）机床设备主要用于学生的金工实习，无法作为他用。因此，每年的设备折旧成为其消耗的成本之一。

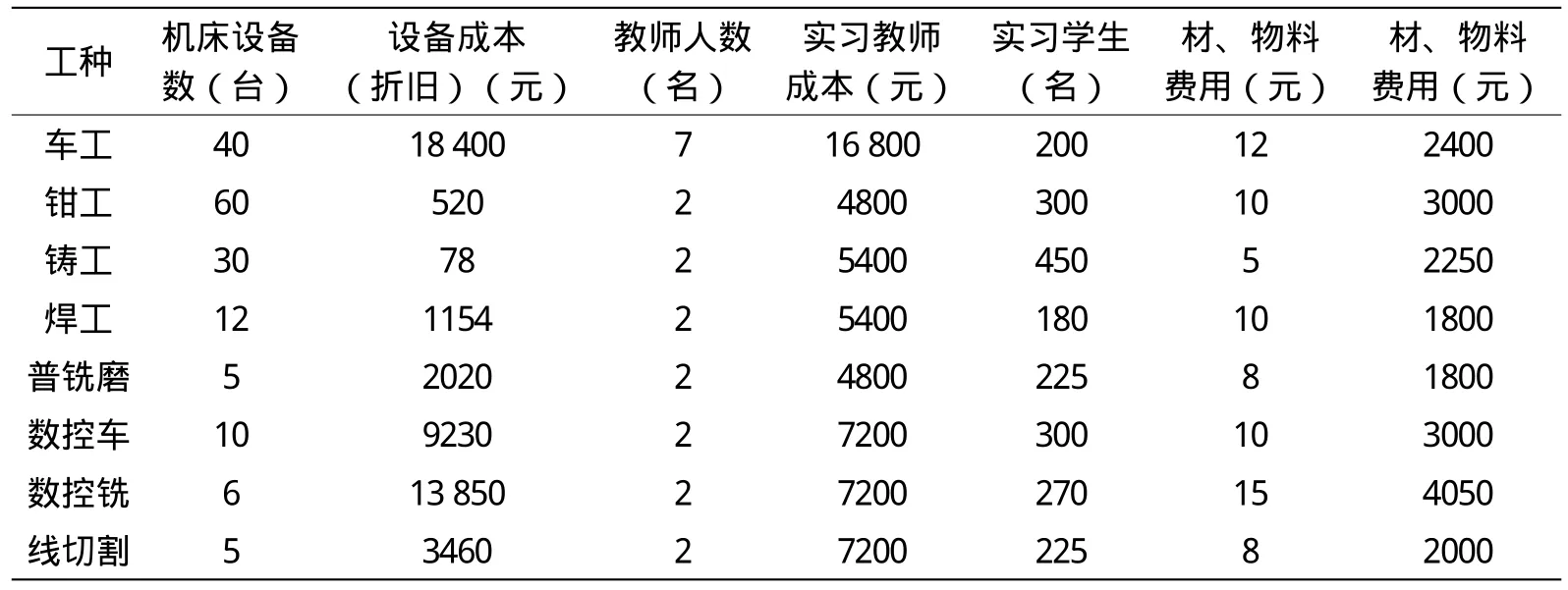
表1 金工实习现阶段资源数据表（15天／批）

2）教师指导金工实习，要有工资收入，这也构成学生参加实习的成本消耗。金工实习中心现有金工实习教师21人，各工种教师工资成本也不尽相同。

3）材料、物料等资源消耗也有一定的成本。

这三部分就基本构成学生参加金工实习的主要资源消耗，如表1所示。

另外，在南京工业大学金工实习中心2012学年的金工实习中，机械类学生的实习时间为四周，非机类学生的实习时间为三周，而全年一共实习40周，因此，全年最多实习14批次学生。由于学生是分成四个大组循环实习，车工、钳工各一个大组，三个数控工种组成一个大组，铸、焊、铣磨为一大组；又由于这次学校投入资金主要用于机床设备的购买，而且先进的数控设备占据多数，而教育部最新规定，在现代数控设备投入上，比例不得低于25%，高可达到50%，每组分担的学生数应基本相同，因此，应有如下约束条件：

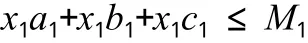
考虑到x1,x2,…,xm的实际意义，要求14≤

x1,x2,…,x8≤28，并且为整数。综合以上条件构成如下线性规划：

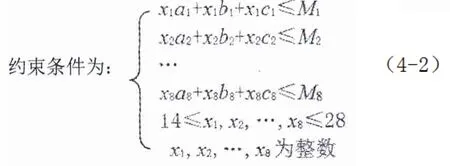
南京工业大学金工实习中心现有车床、铣床、数控铣、数控车、线切割机床等多种设备，总体价值约750万元；现学校决定投入250万元用于购置设备，则机床设备预计价值1000万元，按10年折旧期计算，每年的设备成本约为100万元；学校核定实习教师人数为25人，则工资成本每年约为120万元；另外，学校每年核定35万元机、物料成本费，如表2所示。

表2 金工实习资源限量表

金工实习中心所能容纳实习学生人数最大的线性规划模型为：

约束条件为：

对原问题模型，加入松弛变量转化为标准形式。列出其初始单纯形表如表3所示。

通过数次迭代计算，得出最优解如表4所示。

由于金工实习中心每学年有40周，每周5个工作日，因此，每学期，学生实习接待批次为40×5÷15≈14批，如表5所示。现有金工实习教师必须保证工作量的饱满，14批 要安排的，至于超过14批的学生，需设备、引进新的金工实习教师，投入更多的实习用机、物料来完成。通过上述线性规划的最优解求解，得出结果如表6所示。比较表5、表6，可得表7。

表3 初始单纯形表

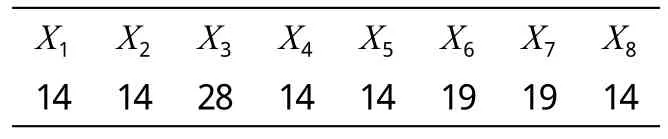
表4 金工实习资源配置最优解

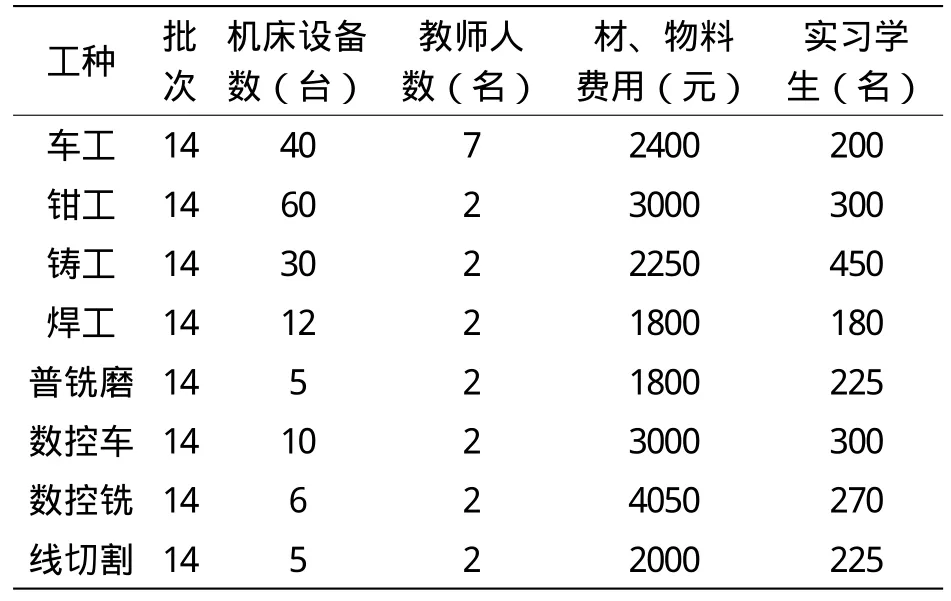
表5 金工实习资源配置表（规划前）

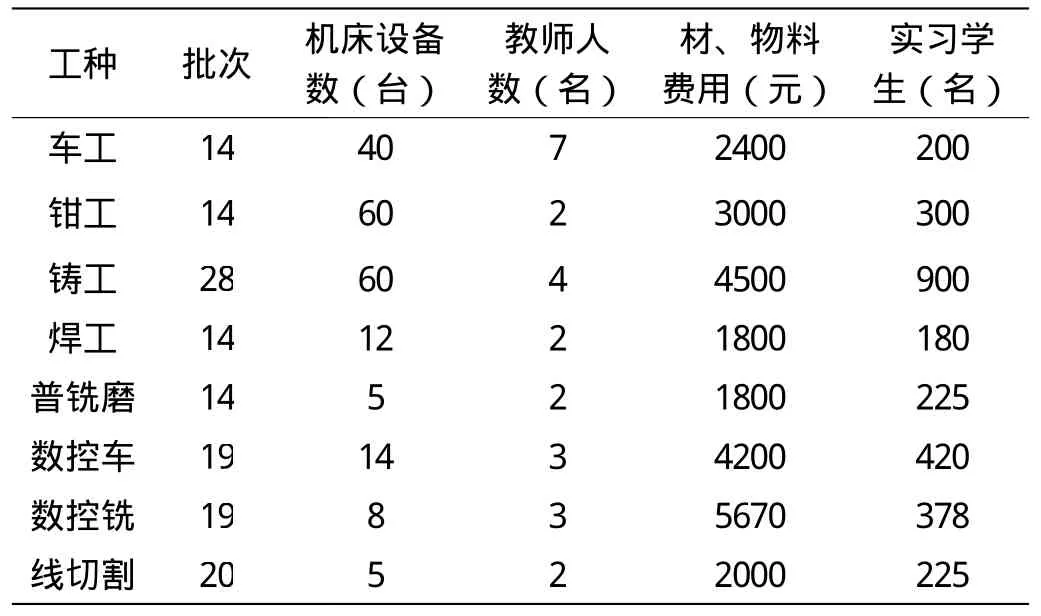
表6 金工实习资源配置表（规划后）

通过表7可以看出，经过对金工实习中心实习资源的线性规划，发现在这次投资中需要在铸工增加60个工位，增加4台数控车床，增加2台数控铣床。另外还需要增加4名金工实习教师，其中铸工两名，数控车、数控铣各一名。在材料、物料的消耗上，每批学生需增加5070元，全年共需增加70 980元。通过这样的投入，铸工每批可承担学生将增加450人，数控车每批可承担学生将增加120人，数控铣每批可承担学生将增加108人，按全年14批计算，共可增加9492人次参加金工实习。

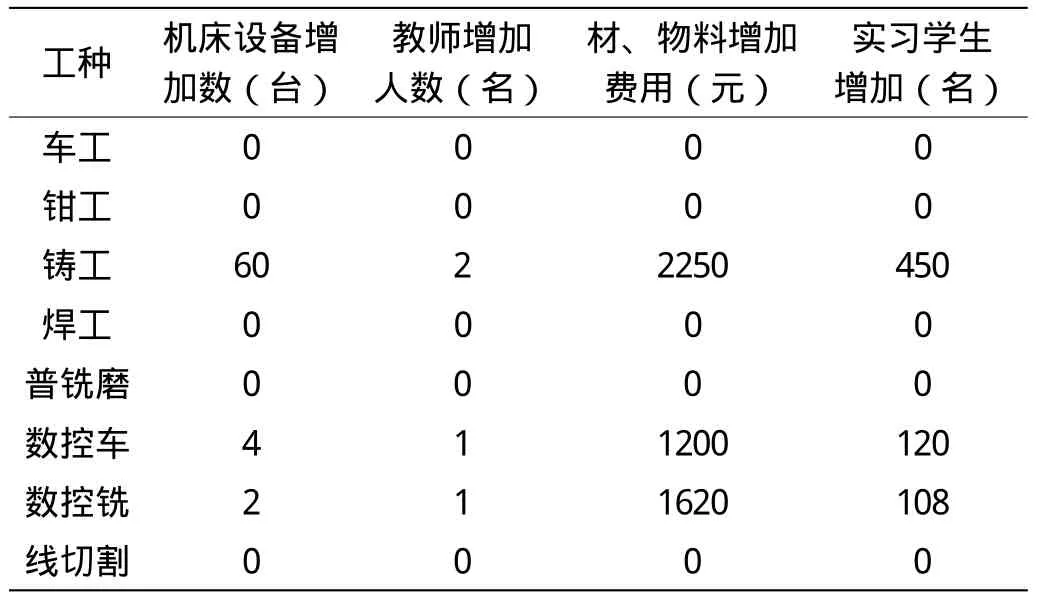
表7 金工实习资源配置变化表（规划后）

结论 通过求解线性规划模型，获得南京工业大学金工实习资源优化的最佳结果。并依据此结果，可以得出，在此次对金工实习中心的投资中，应对铸工、数控车、数控铣这三个工种进行设备、实习教师、材料费用等方面的加大投入，这样，金工实习中心就能够尽可能多地容纳实习学生。

5 结束语

本文将理论和实际结合起来，通过建立金工实习中心实习资源线性规划模型，运用线性规划求解法中的单纯形法求解，对实习设备、实习教师和实习所用机物料三种资源在各工种之间作了优化配置，并利用此结果，用新投入的资金购买资源对各工种进行合理配置。但是，由于单位机物料消耗成本，单位人工成本、设备成本、设备折旧都是根据以往的数据和经验假设的，随着物价水平等一系列因素的影响，其数值将不可避免地产生偏差，这也将会影响到线性规划求解的准确性。

[1]钱颂迪.运筹学[M].北京:清华大学出版社,1995.

[2]吴清烈,等.运筹学[M].江苏:东南大学出版社,2004.

[3]唐大超.应用线性规划提高材料利用率[J].十堰职业技术学院学报,2007(12):100-104.

[4]钟仪华.利用多约束水平线性规划方法建立油田开发产量分配优化模型[J].石油规划设计,2007(11):5-8.

[5]张学鲛.线性规划在工期资源优化中的应用模型[J].建造技术,2009(1):49-51.