三维结构水中刚弹耦合运动附加质量特性分析

刘 莹,杨 衡,王毅娜,王庆周,张阿漫

(哈尔滨工程大学船舶工程学院，黑龙江 哈尔滨 150001)

三维结构水中刚弹耦合运动附加质量特性分析

刘 莹,杨 衡,王毅娜,王庆周,张阿漫

(哈尔滨工程大学船舶工程学院，黑龙江 哈尔滨 150001)

三维结构在水中做非定常运动时伴随着附加质量力的影响，从而其运动特性会发生一定的变化，附加质量是表征水下航行体的水动力性能的一个重要参量。基于有限元软件，根据势流理论，采用格林函数方法分别计算刚体、弹性体及结构刚弹耦合的附加质量，同时考虑各影响因素对附加质量的影响程度，对其各方面特性进行研究分析， 最终得到对结构水动力研究有重要影响的结论。

附加质量；格林函数；影响因素；刚弹耦合

0 引言

水下航行体在水中做非定常运动时，会产生附加质量的作用从而改变其运动特性，附加质量是表征水下航行体的水动力性能的一个重要参量，因此附加质量特性的研究对于研究水下航行体水动力具有十分重要的意义。影响附加质量的因素有很多，如物体运动状态、物面形状、弹性体的振动模态等，这些影响因素都是研究的重点所在。

人们对于附加质量特性的研究已有多年的历史，在通过实验发现了附加质量现象以后，对附加质量特性的进一步研究也逐渐展开。21世纪，David Clarke推导出了浅水中圆柱体的附加质量系数公式，林超友、朱军[1]采用Hess-Smith方法计算了物体近边界运动时附加质量，对于结构刚性和弹性运动的附加质量研究人们已取得了一定的成果。但对于高速运动的水下航行体，由于受到高频砰击作用，其弹性运动十分剧烈，因此，刚弹耦合效应将变得更加明显，对于结构刚弹耦合附加质量的研究也成为了重点。本文在研究刚体弹性体附加质量特性的同时，进一步计算了结构刚弹耦合的附加质量，在验证方法有效性的基础上计算附加质量的变化，并进行分析比较得出相应结论。

1 刚弹耦合附加质量的计算

根据势流理论[2]，水下非定常运动结构附加质量的计算公式为：

(1)

式中：λ为附加质量；φ为单位速度势；ρ为流体密度。

因此求得φ即可得到结构的附加质量，采用频域格林函数方法可得总的速度势，便可利用相关理论编写频域格林函数的程序并进行数值计算。频域格林函数G满足拉普拉斯方程以及除去自由面条件以外的下面各条件：

(2)

式中：v为结构运动速度，k为波数。

可得到无限水深三维频域无航速格林函数为：

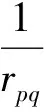
J0(kR)dk+i2πvev(z+ζ)J0(vR)

(3)

式中：p为域内的静点；q为动点；rpq为点p到q的距离；J0为从直角坐标系到局部坐标系上的雅克比转换。

下面计算弹性体的附加质量[3]。由结构动力学可知，将结构视为连续弹性体，连续弹性体在水中运动的方程式可化为：

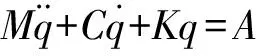
(4)

(5)

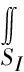
(6)

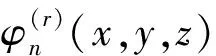
(7)

式中：g为重力加速度；ωz为流固交界面上的轴向位移分量。

在规则波的作用下，结构做微幅简谐运动，根据线性叠加原理，满足Laplace 方程和边界条件的速度势为：

Φ=Re((ΦI+ΦD+ΦM)eiωt]

(8)

式中：ΦI为入射波速度势；ΦD为绕射速度势；ΦM为辐射速度势。

设稳态解qr为：

qr=Re(Qreiωt),r=1,2,…,n

(9)

式中：Qr为复数。

并设由于结构运动产生的速度势为:

(10)

式中：Φr为对应于第r干模态的速度势。

(11)

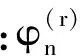
故由式(11)可得第r干模态的广义力为：

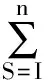
(12)

式中：Fr为广义波浪激励矢量F的元，且

F=(F1,F2,…,Fn)T

(13)

2 刚体附加质量分析

2.1数值方法有效性验证

取半径为1 m的不同长度圆柱体，以圆柱体扰流为计算模型，用频域格林函数的数值解法计算圆柱体刚体运动的附加质量[4,5]，如图1所示。

图1 圆柱体边界元模型

圆柱水下绕流单位长度附加质量的理论解为πR2，R为圆柱体半径。图2为不同长度圆柱体计算所得附加质量与理论值的对比情况，最大误差不超过4.96%，因此，本文数值解有较高的精度，验证了用此方法计算刚体附加质量的正确性和有效性。

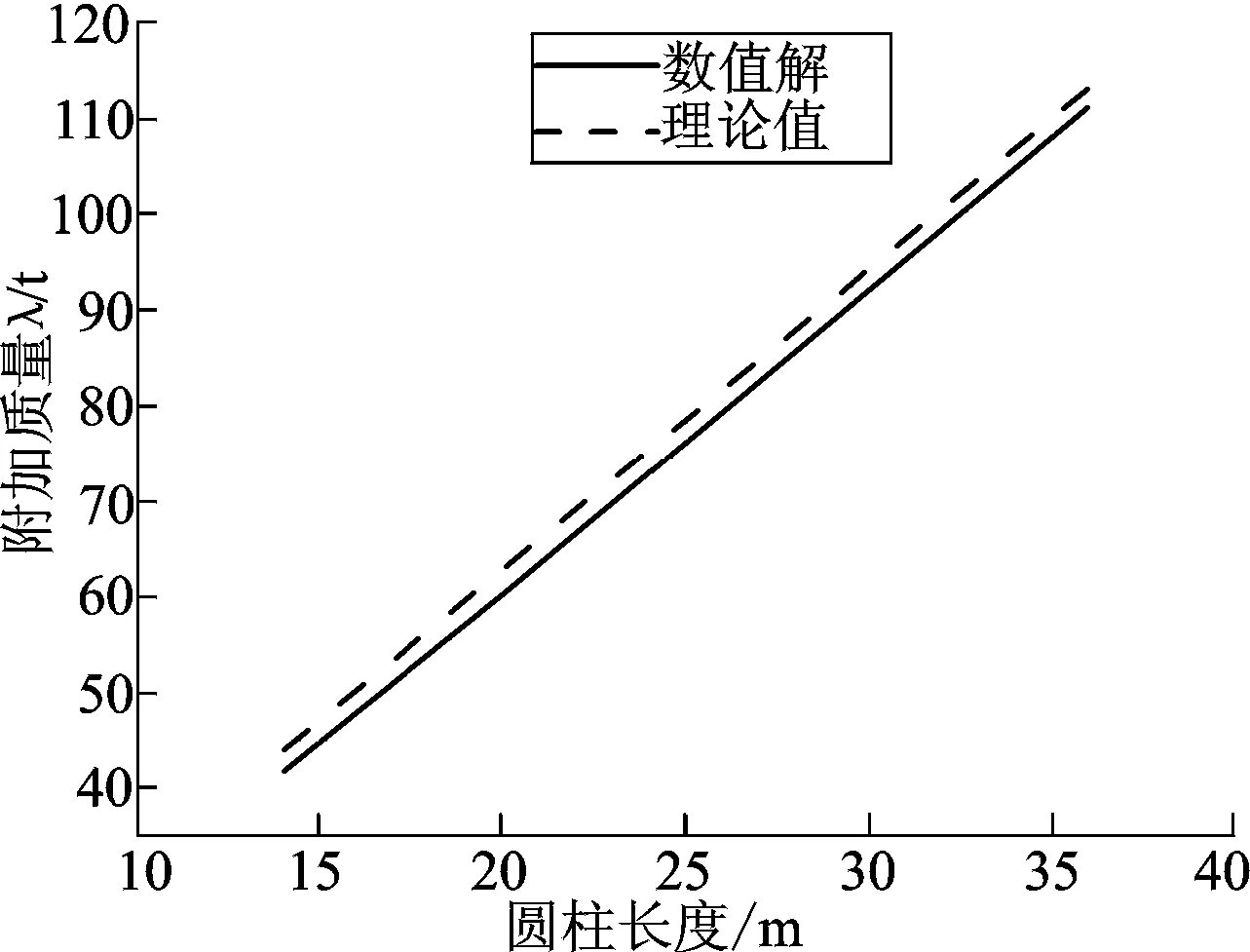
图2 圆柱体刚体运动附加质量与理论值对比

2.2刚体附加质量的影响因素

2.2.1圆柱壳出水过程附加质量的变化分析

圆柱壳出水时，其湿表面积随着出水过程逐渐减小，会对附加质量产生影响。圆柱壳出水示意图如图3所示，H为出水高度。

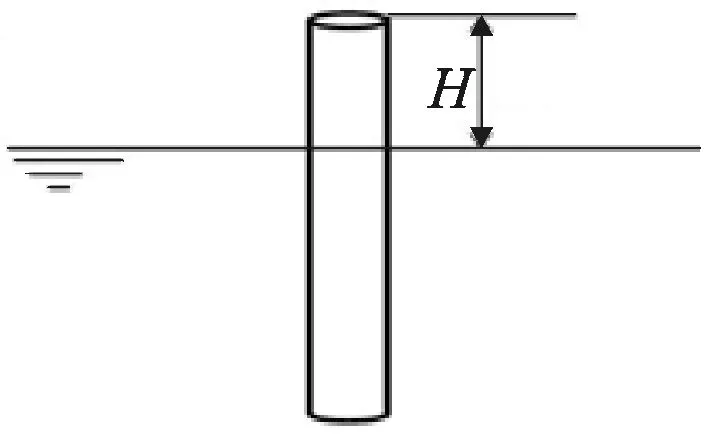
图3 圆柱壳出水示意图

以直径1 m、长10 m、壁厚10 mm两端自由的圆柱壳体为例，利用频域格林函数的数值解法研究其x方向刚体运动附加质量随出水高度的变化，结果如图4所示。从图4可以看到，附加质量随出水高度的减小而减小，与圆柱壳体湿表面积成反比例的关系。

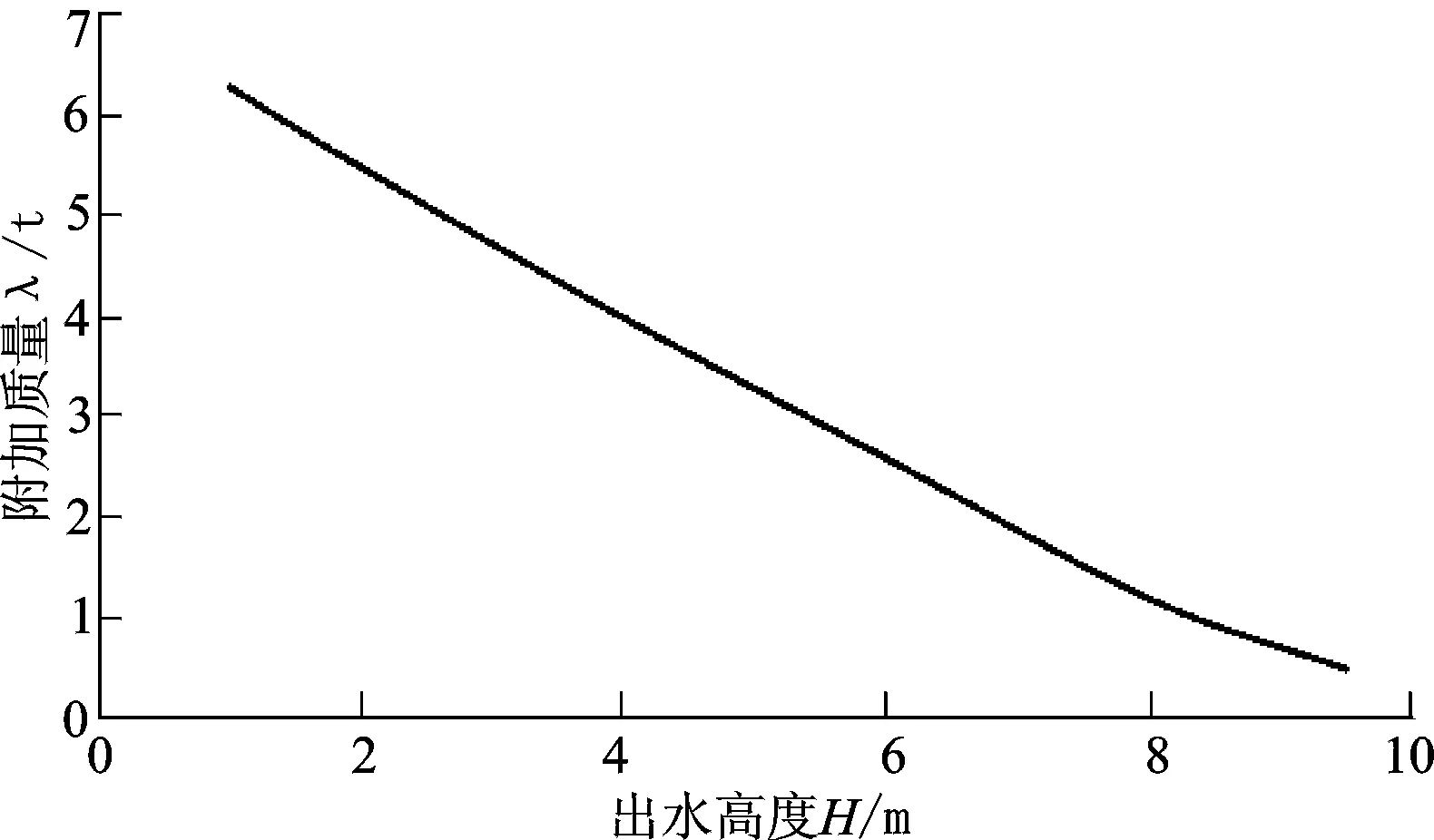
图4 附加质量随出水高度的变化

2.2.2空泡发生对三维圆柱壳附加质量的影响

部分航行体在水下运动时会有空泡的产生。空泡发生时会使湿表面积减小，同样会对附加质量产生影响。空泡长度示意图如图5所示。

同样以直径1 m、长10 m、壁厚10 mm两端自由的圆柱壳体为例，以同样的数值方法计算其x方向刚体运动附加质量随空泡长度的变化。计算速度势时将空泡作为柱体的一部分，计算附加质量时将这部分扣除，得到圆柱体x方向附加质量随空泡长度变化关系如图6所示。

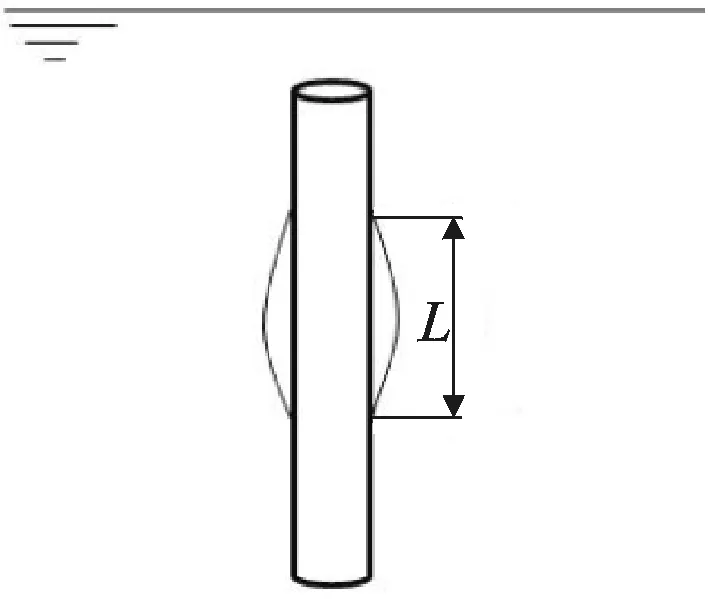
图5 空泡长度L示意图

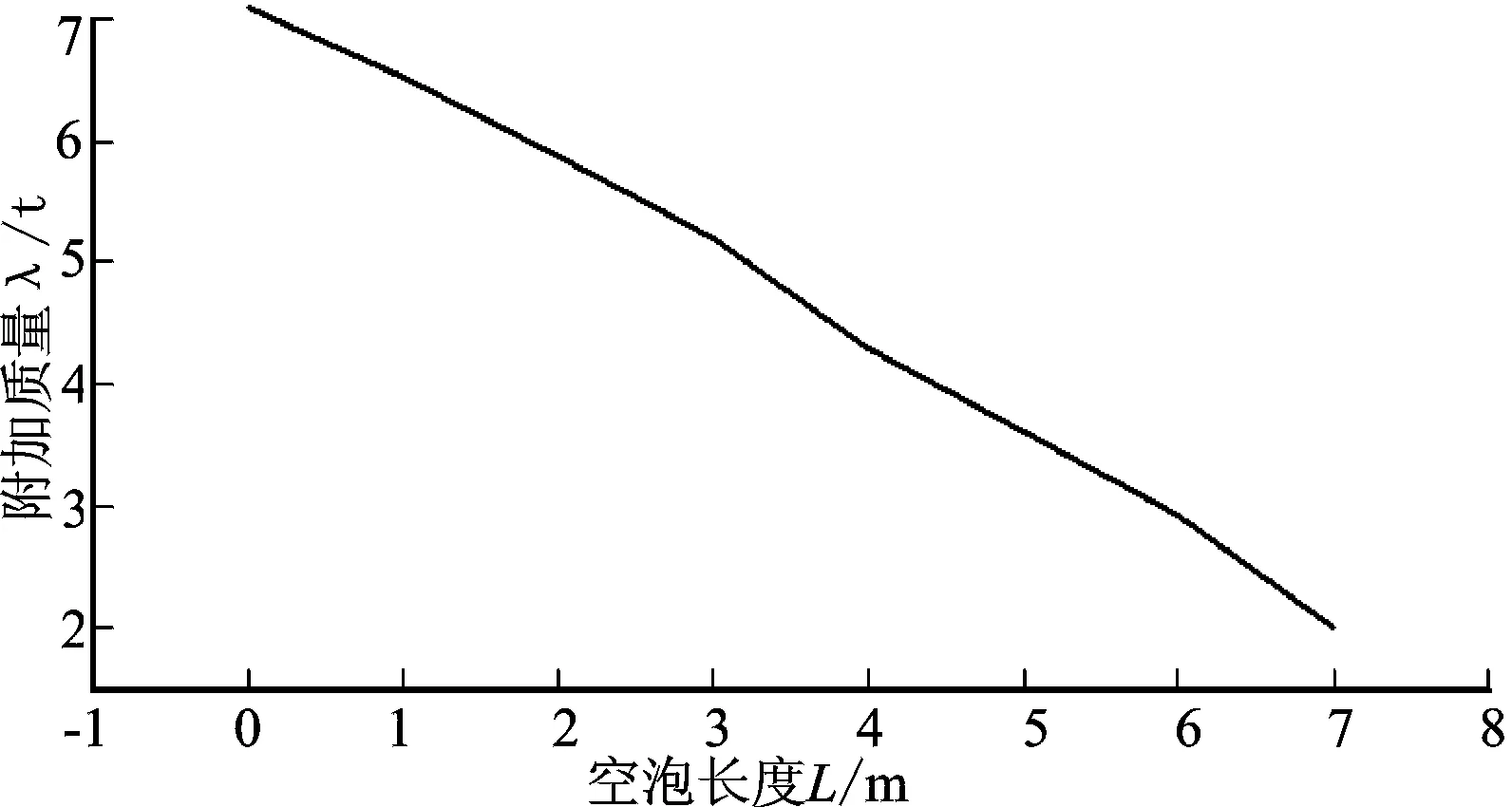
图6 附加质量随空泡长度变化

综合以上分析结果可以看出，在未发生空泡时，无论是圆柱壳出水还是发生空泡，均为减小了湿表面积从而引起附加质量的变化，圆柱壳刚体运动的附加质量随湿表面积的减小而减小。

3 弹性振动附加质量

3.1程序有效性的验证

为了对弹性体附加质量数值解进行验证，取某一柱体在水中做弹性振动为计算模型。根据《中华人民共和国国家军用标准》[6]对附加质量的计算，潜艇在水下潜航状态附连水质量的估算公式：

mv=Kiμv(α,β)πρB2

mh=Kiμh(α,β)πρC2

(14)

式中：mv是轴向振动引起的附加质量；μv(α,β)为水下轴向二维附加质量修正系数；α、β为参数。

以半径1 m、长13 m的柱体水中绕流模型为例计算弹性体振动附加质量的数值解，并与式(14)的估算结果相比较，从而验证弹性体振动附加质量数值计算方法的正确性。

在一阶振动模态时，经验解为26.726，本文数值解为24.642，相对误差为7.8%。

2种方法计算的附加质量结果存在一定的差异，但在10%以内，说明本文的计算方法是可行的。

3.2弹性体附加质量的影响因素

建立4个不同的圆柱壳模型，模型的长度都为10 m，半径都为0.5 m，只是边界条件和壁厚不同。模型的材质为钢材，密度为7 850 kg/m3，弹性模量为2.1×1011Pa，钢材泊松比为0.3，设水深为10 m。对4种模型进行模态分析[7]，4种圆柱壳模态分析结果见表1。

3.2.1模态对弹性体附加质量的影响

分别计算4种模型在不同振动模态下的附加质量，通过对比每个模型不同振动模态下的附加质量的值而得出模态对弹性体附加质量的影响规律，如图7～10所示。

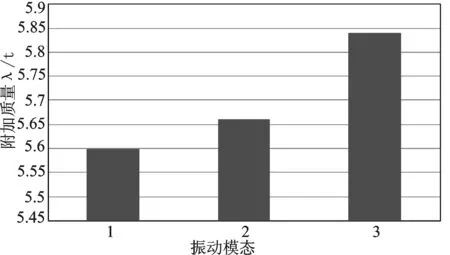
图7 模型1的弹性振动附加质量

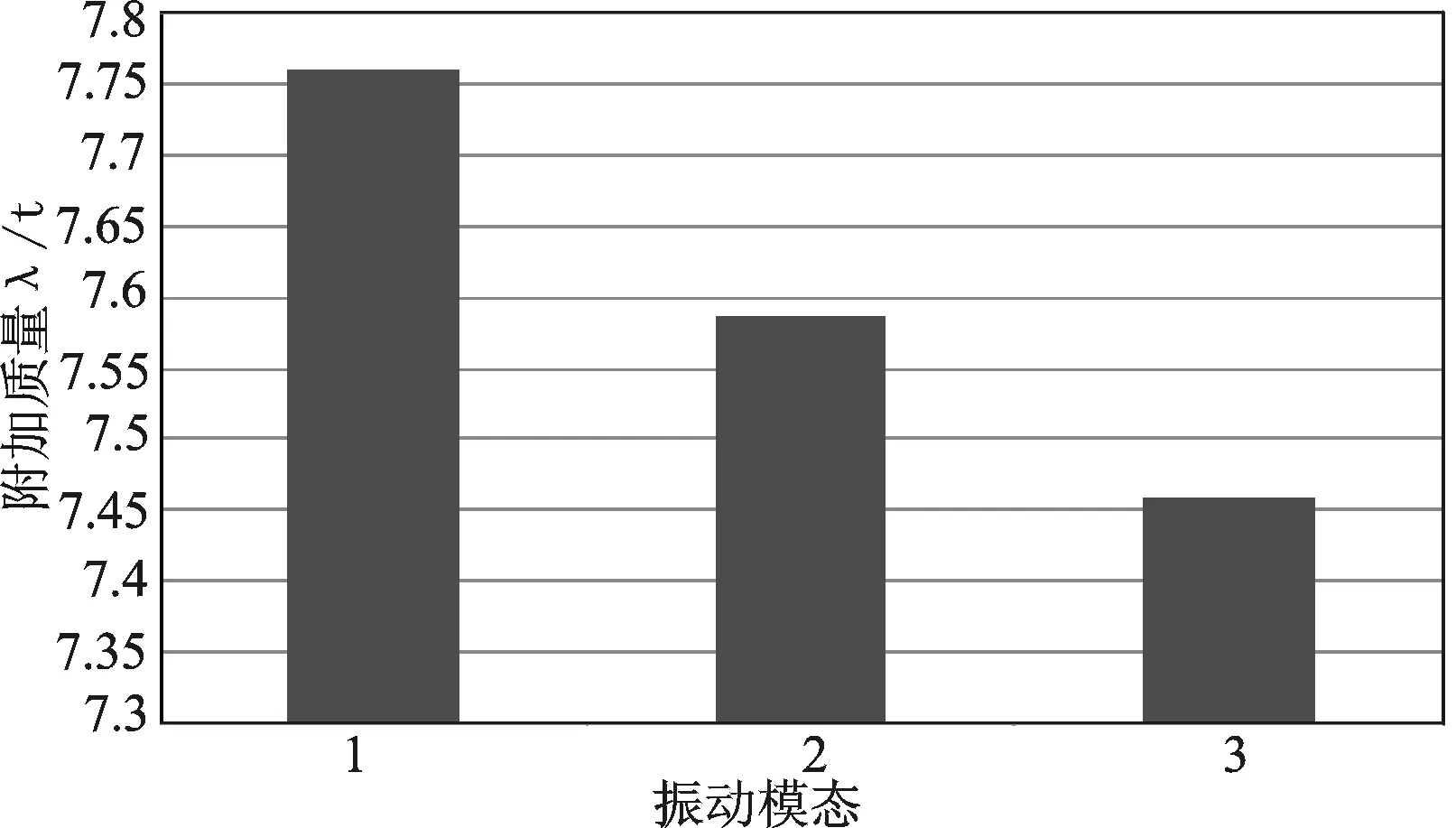
图8 模型2的弹性振动附加质量

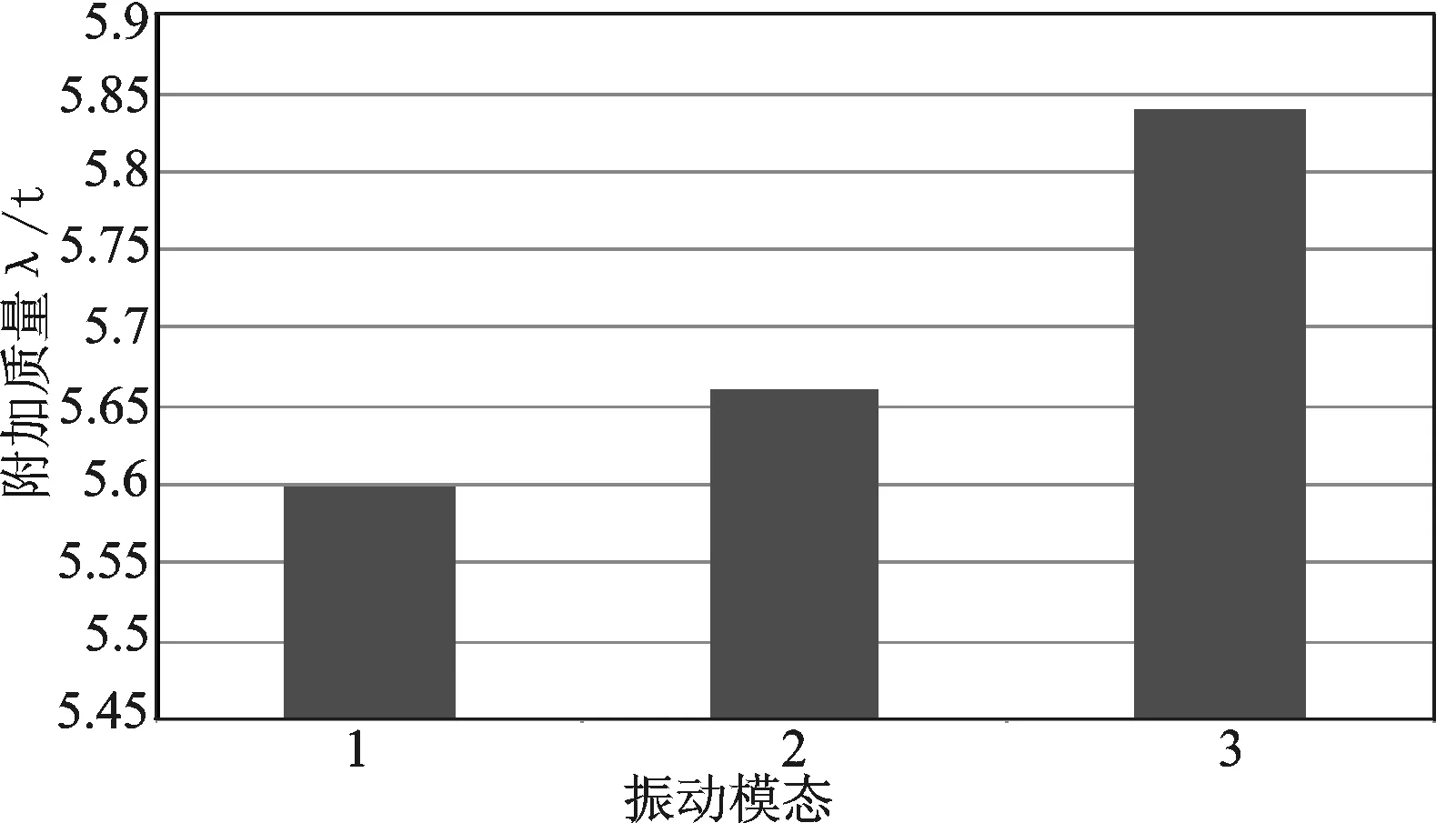
图9 模型3的弹性振动附加质量

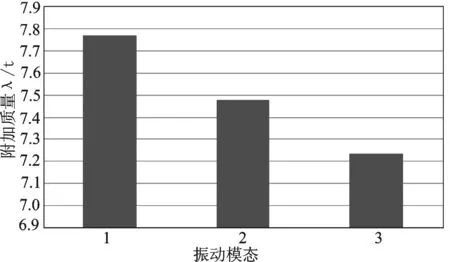
图10 模型4的弹性振动附加质量

由以上图表可以看出，振动模态会对弹性振动附加质量产生影响。对于两端自由的水下三维圆柱壳结构，振动模态越高其水下振动附加质量越大；而对于两端刚性固定的水下三维圆柱壳结构，振动模态越高其水下振动附加质量越小。这是因为边界条件影响了三维圆柱壳的阵型，因此需进一步讨论边界条件对弹性体附加质量的影响。

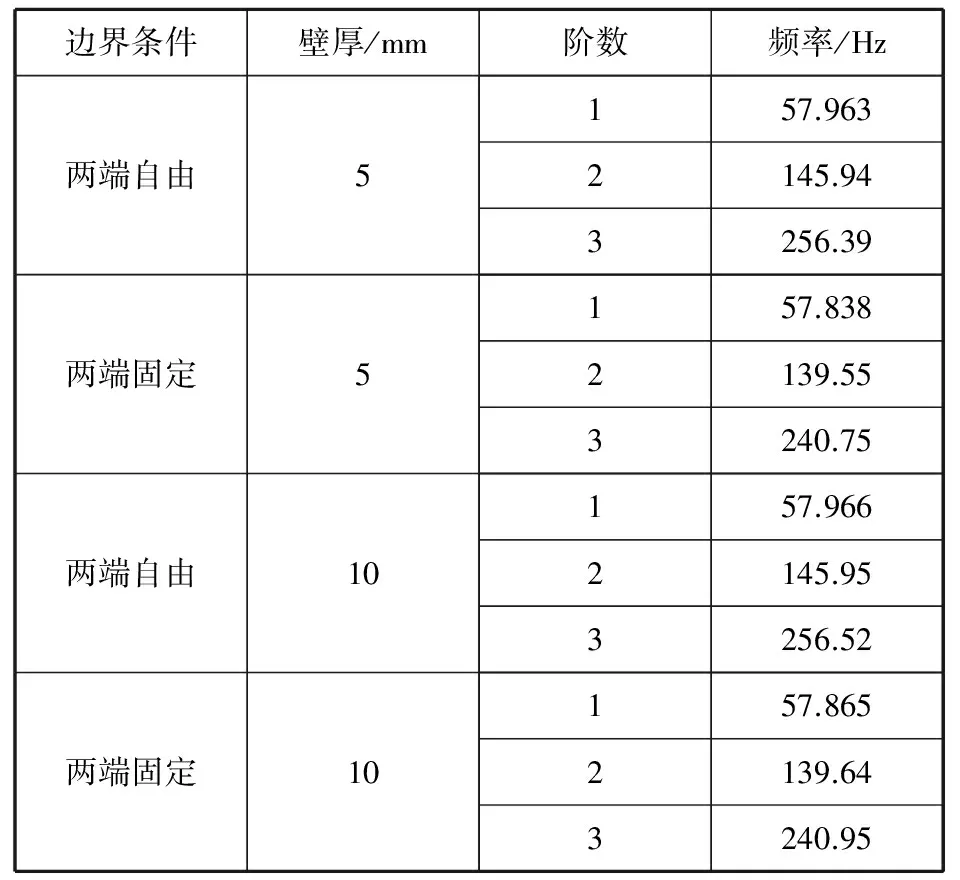
表1 圆柱壳模态分析结果

3.2.2边界条件对弹性体附加质量的影响

将以5 mm壁厚的圆柱壳为例，讨论边界条件对同一尺寸的模型弹性振动附加质量的影响。分别计算三维圆柱壳结构在一阶、二阶、三阶振动模态时，不同边界条件下的附加质量，结果如图11～13所示。

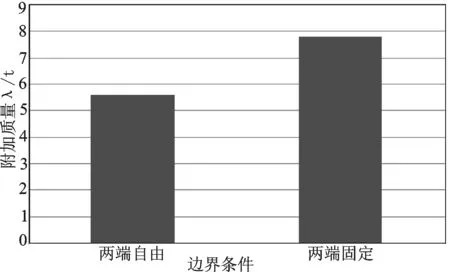
图11边界条件对一阶振动附加质量的影响

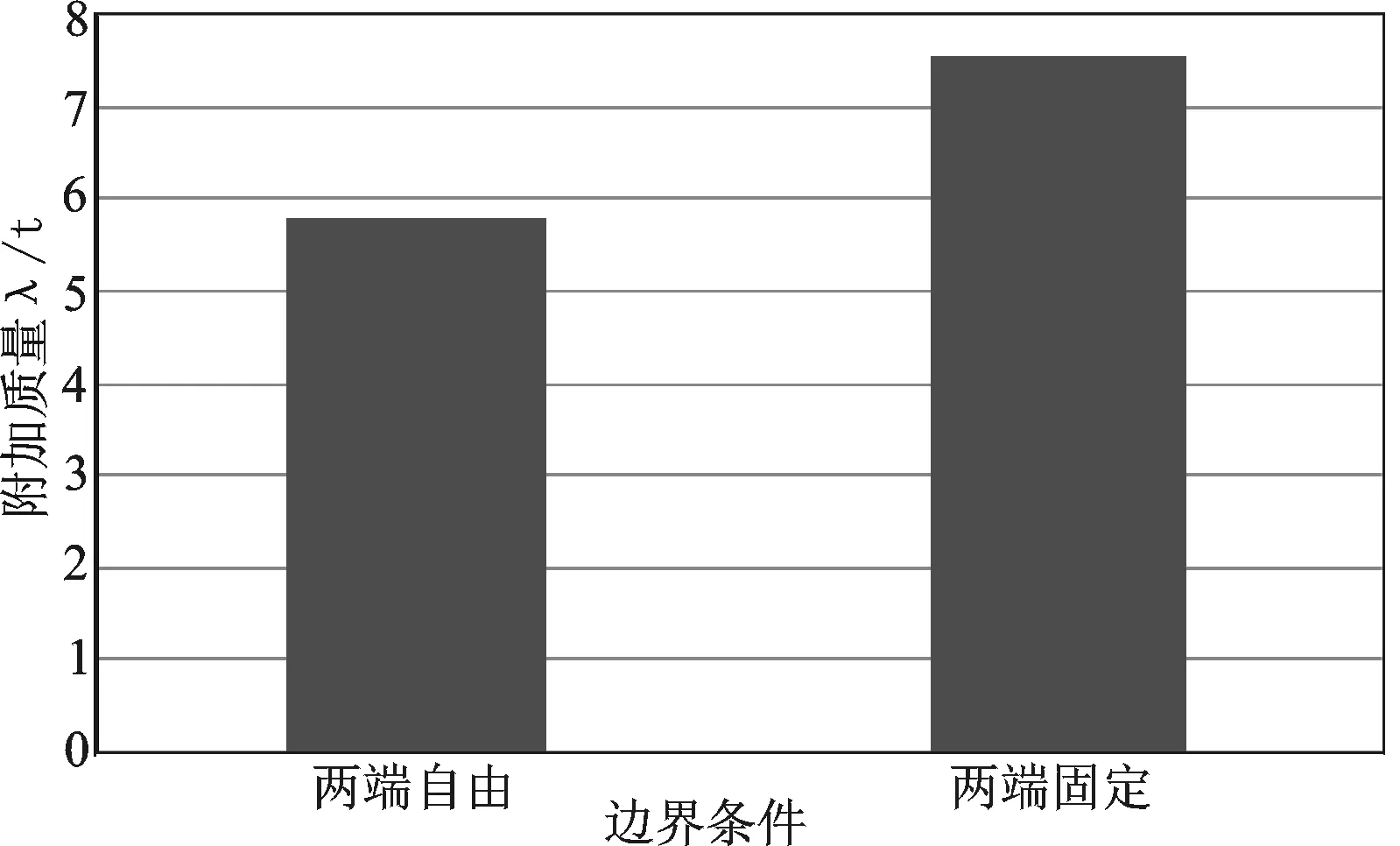
图12 边界条件对二阶振动附加质量的影响

由图11～图13可以看出,其他条件相同时，三维圆柱壳结构两端刚性固定的弹性振动附加质量要大于两端自由的弹性振动附加质量。这是因为边界条件的不同导致三维圆柱壳的阵型不同，阵型不同而引起附加质量的不同。

3.2.3壁厚对弹性体振动附加质量的影响

以一阶弹性振动为例，研究壁厚对弹性振动附加质量的影响。分别计算边界条件为两端自由时和刚性固定时壁厚对弹性振动附加质量的影响，结果如图14、图15所示。

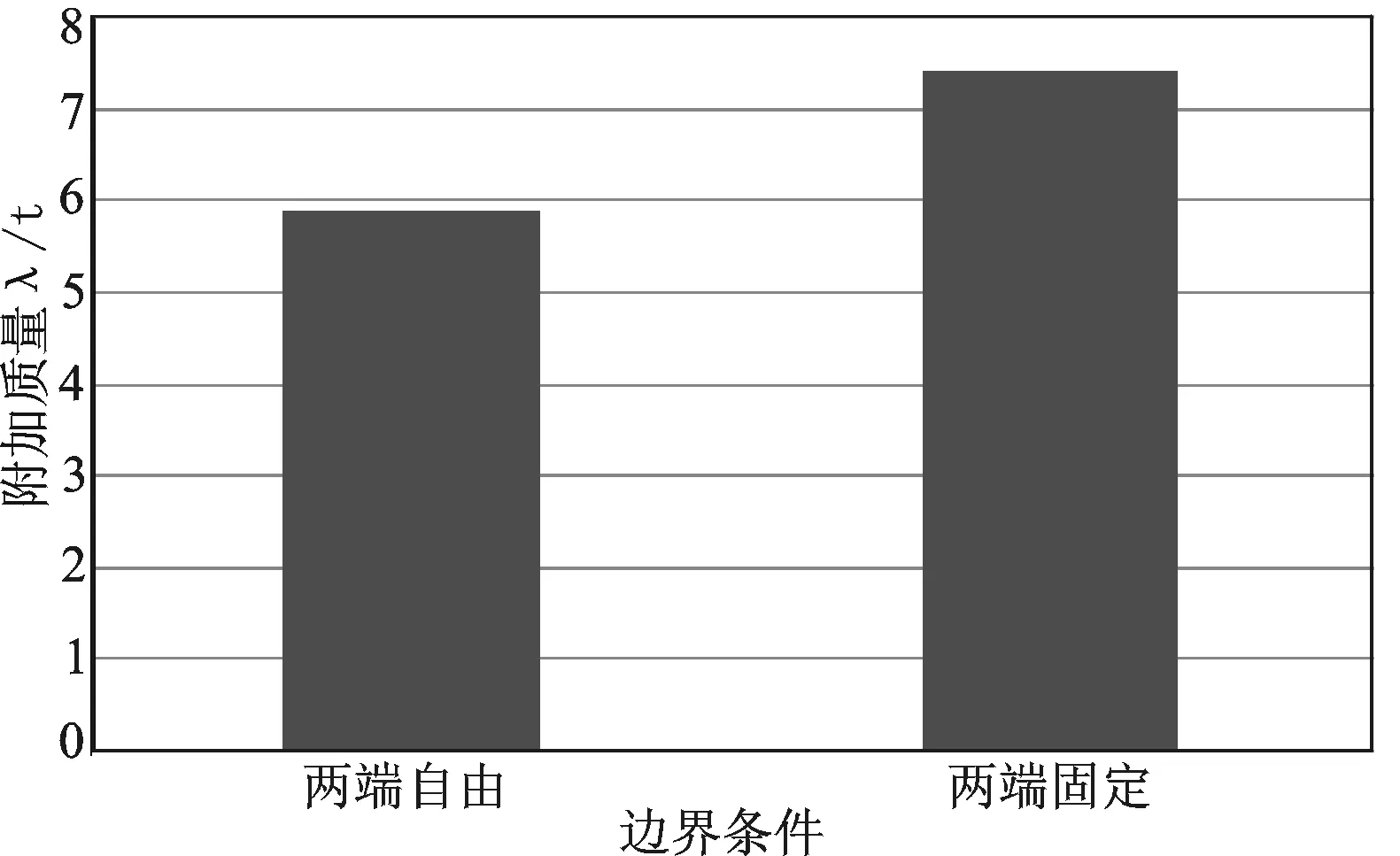
图13 边界条件对三阶振动附加质量的影响

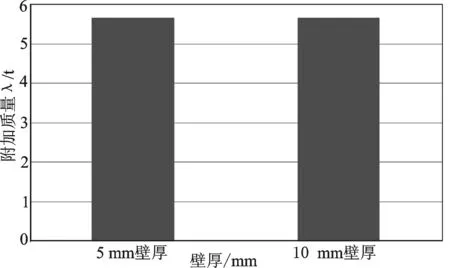
图14 壁厚对两端自由圆柱壳附加质量的影响

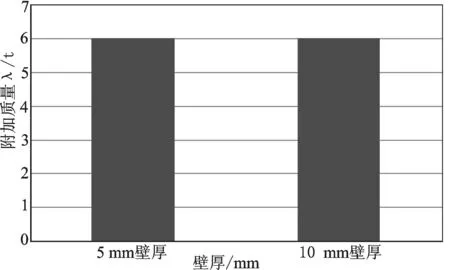
图15 壁厚对两端刚性固定圆柱壳附加质量的影响

从以上图表可以看出，在结构和其他条件相同时，壁厚对附加质量没有显著的影响，这一点可以从附加质量的定义中看出来。由于壁厚对速度势没有很大影响，因此不会影响附加质量的大小。

3.3附加质量的对比

选取5 mm壁厚两端自由的三维圆柱壳模型，水深设为10 m，比较其不同方向上的刚体运动附加质量、弹性振动附加质量、刚弹耦合附加质量[8]。

对比结果如图16所示：x、y、z分别为3个方向的刚体运动附加质量，1、2、3分别为3个方向弹性振动附加质量，其余各量代表刚体、弹性体附加质量在各个方向上的耦合值。

从图16中可以看出，x、y方向上的附加质量远大于z方向上的附加质量，这与圆柱壳的形状有关。z方向上的截面积较小，所以附加质量较小。三维圆柱壳的弹性振动附加质量大于刚体运动附加质量。三维圆柱壳耦合附加质量最小且与y方向的耦合附加质量最大，这与圆柱壳的振动方向有关，弹性振动与其他方向基本没有耦合。

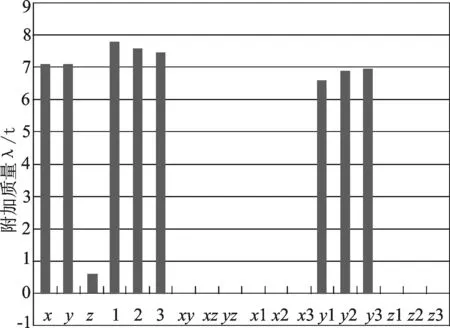
图16 刚体运动附加质量、弹性振动附加质量、刚弹耦合附加质量的对比

4 结论

本文通过分别计算刚体、弹性体和结构刚弹耦合的附加质量并进行分析，得出了以下结论：

(1)结构刚体运动附加质量与水深无关，与结构的湿表面积有关，并成正比例的关系。

(2)振动模态会对弹性振动附加质量产生影响，但是不是唯一的，会因边界条件的不同而产生相反的影响。对于两端自由的水下三维圆柱壳结构，振动模态越高其水下振动附加质量越大；而对于两端刚性固定的水下三维圆柱壳结构，振动模态越高其水下振动附加质量越小。

(3)三维圆柱壳水下振动的耦合附加质量与其振动方向有关。与其振动方向相同的方向上的耦合附加质量比较大，而其他方向上的耦合附加质量比较小。

[1]林超有，朱军. 潜艇近海底航行附加质量数值计算[J].船舶工程,2003，25(1)：26-29.

[2]戴遗山，段文洋. 船舶在波浪中运动的势流理论[M]. 北京：国防工业出版社, 2008.

[3]刘成刚.潜艇附加质量计算及其水中振动特性研究[D].哈尔滨：哈尔滨工程大学,2011.

[4]倪宝玉，孙士丽，孙龙泉，张成.弹体落水过程中附加质量变化影响研究[J].振动与冲击,2012，31(14)：171-176.

[5]Hulme A.The wave acting on a floating hemisphere undergoing forced periodi oscillations[J].J FluidMech,1982,121：443-463.

[6]GJB 4000-2000，舰船通用规范[S].

[7]姚熊亮.船体振动[M].哈尔滨：哈尔滨工程大学出版社，2004.

[8]Zhang Y L， Yeo K S，Khoo B C, Wang C. 3D jet impact and toroidal bubbles[J]. Comput. Phys., 2001,166(2)：336-360.

2013-09-12

刘莹(1990-),女,硕士，研究方向为流固耦合动力学；杨衡(1986-),男,博士，研究方向为流固耦合动力学；王毅娜(1991-),女,硕士，研究方向为流固耦合动力学；王庆周(1988-)，男，硕士，研究方向为流耦合动力学；张阿漫(1981-),男,博士生导师，研究方向为流固耦合动力学。

U661.4

A