基于零值补偿和EMD的加速度积分误差消除方法

冯 锟,冯建兰

(1武汉大学 电气工程学院,湖北 武汉 430072;2湖北理工学院,湖北 黄石 435003)

基于零值补偿和EMD的加速度积分误差消除方法

冯 锟1,冯建兰2*

(1武汉大学 电气工程学院,湖北 武汉 430072;2湖北理工学院,湖北 黄石 435003)

为探求加速度积分误差的消除方法，利用频谱对实测加速度数据进行分析,以误差频率和理想的加速度变化曲线来评价误差。采用基于零值补偿和经验模态分解(Empirical Mode Decomposition，EMD)的方法，对实测数据进行了误差校正与评价，实践证明该方法能有效消除积分算法中的误差。

加速度传感器；频谱分析；误差评价；经验模态分解

工程振动量值的物理参数常用位移、速度和加速度表示。由于用加速度传感器测量加速度信号具有测量操作方便、处理速度快等优点,所以，常用于动态测量振动位移量的大小。然而在实际工作中，由于物理原因，加速度传感器测量信号通常存在误差，一般的消除方法有：基于通频带扩展的动态补偿法[1]、基于消除趋势项的低频衰减算法[2]、基于噪声去除的移动平滑滤波算法[3]等。

文中提出了一种新的方法：基于零值补偿和EMD的加速度积分算法的误差补偿。此法从系统误差和随机干扰2个方面，对误差信号进行了消除。同时，还应用了零值补偿运算的快速性和经验模态分解对非平稳信号的适应性，显著地消除了加速度信号的误差。

1 实测加速度直接积分法的误差及其评价

1.1采集电机振动的加速度数据

电机的运行状态对电力系统的稳定与安全有着重要作用。当电机处于异常状态时，若不能及时处理，就会发生故障。因而，对电机振动的分析与测量就显得很重要。在实际工作中振动量的大小一般用加速度的值来度量，电机振动检测的原理图如图1所示。

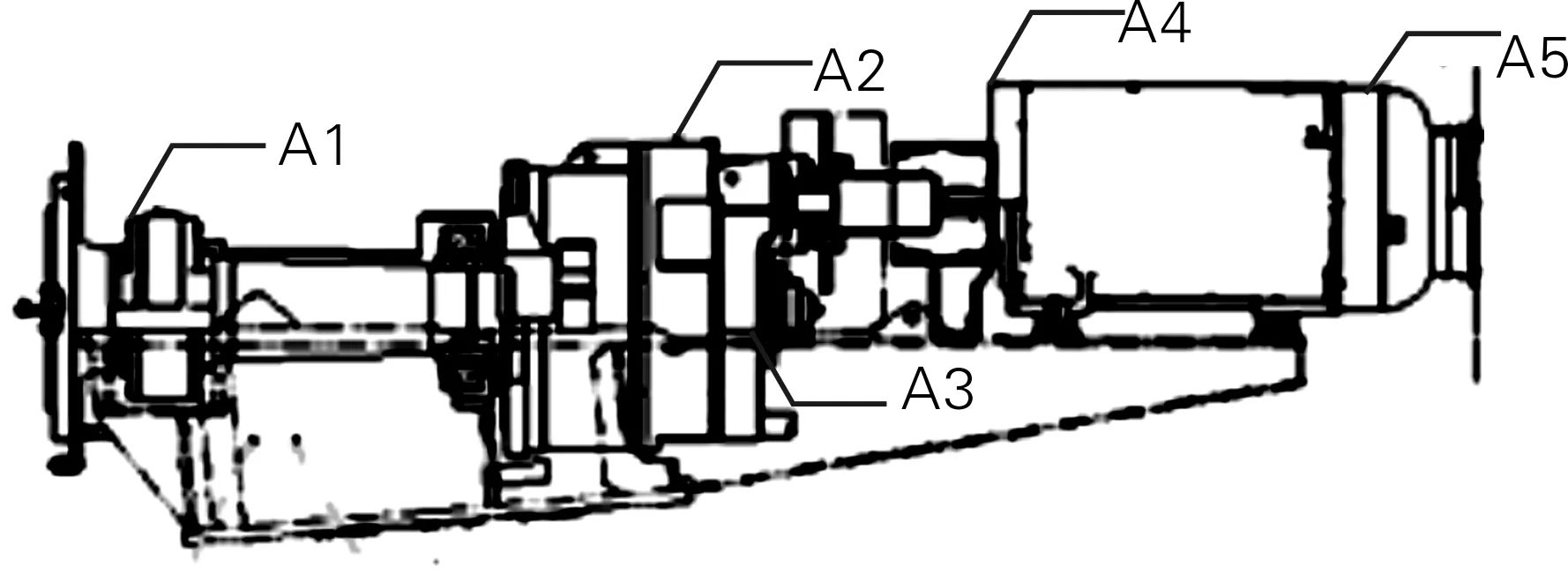
图1 电机振动检测的原理图

在图1中，A1～A5表示电机主轴和定子等部位，安装有加速度传感器来测量振动加速度，对实测数据进行积分，就可得到振幅、位移。用不同方法采集到3组加速度传感器的数据：

1)单方向从A点运动至B点；

2)从C到D后再返回到C；

3)从E点到F点，再由F到E，并再重复一次，电机振动示意图如图2所示,其初速度皆为0。将这3组运动状况所测量的结果分别标记为A、B、C组。

图2 电机振动示意图

1.2加速度实测数据变化的误差分析

1.2.1实测数据变化的频谱分析

统计测量得到的A、B、C 3组原始数据在时域中的分布，发现有些时刻加速度数据趋于零，要将它们作为无效值剔除来分析主要频谱和干扰频率[4]。用matlab对原始加速度数据进行傅里叶变换，得到的加速度频谱图如图3所示。

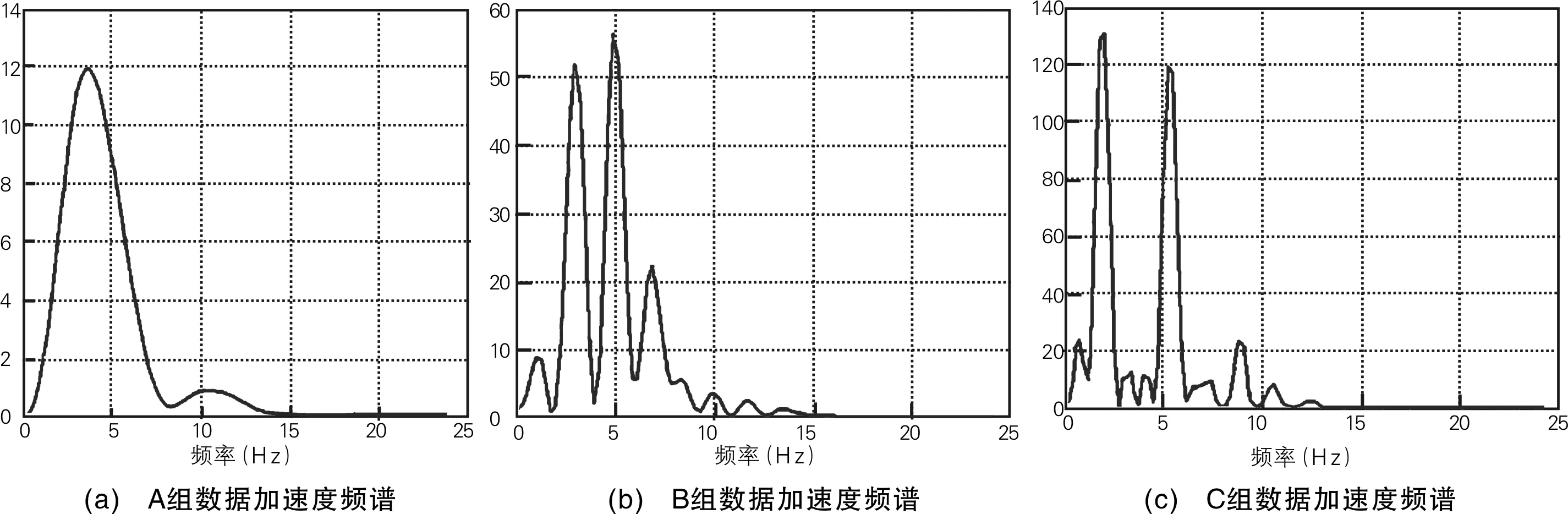
图3 加速度频谱图

比较图3中各组的频谱可知，3组加速度对应的频谱有显著特征，对幅度较高的频率进行数据分析，各组加速度主要频率如表1所示。

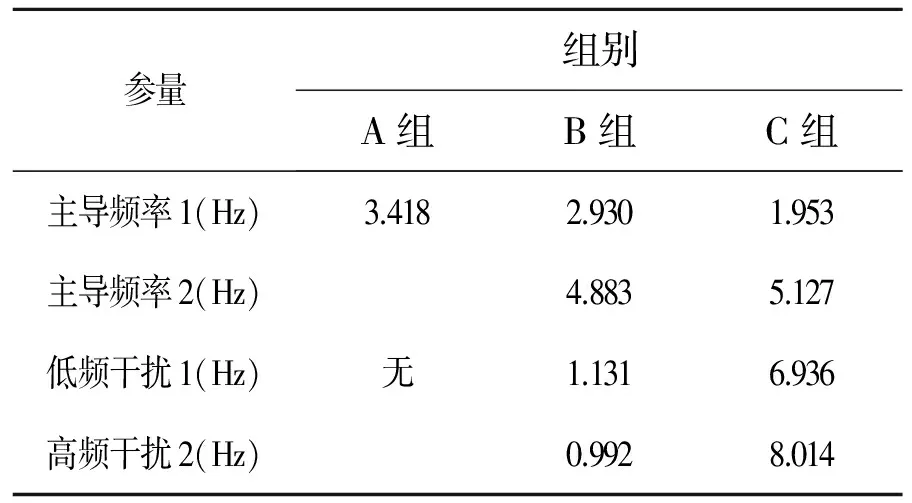
表1 各组加速度主要频率

发现A组运动的加速度频率单一，但频谱主瓣较大；而B、C 2组存在2个主导频率，有一定的频率分裂，运动过程的复杂程度对加速度测量数据有显著影响。测量信号存在系统误差，1Hz左右的低频干扰使得信号总偏向于时间轴的一侧；同时存在随机误差，产生不同频率的高频干扰使得加速度信号在时域变化上有噪声干扰。

1.2.2加速度变化的理想方程

利用主导频率的幅频、相频特性构造理想加速度方程如下：

at=A1sin(ω1t+φ1)+A2sin(ω2t+φ2)+…+Aisin(ωit+φi)

(1)

式(1)中，ωi为理想运动频率的频率，Ai和φi分别为分解之后的理想运动频率对应的幅值和相值。将各组的主导频率标记为理想情况下的运动频率，求得各自在主导频率下的幅频、相频特性，A、B、C组加速度理想方程分别为：

at=12.03sin(2π×3.418t+2.637)

(2)

at=51.83sin(2π×2.930t+2.352)+

56.24sin(2π×4.883t-1.345)

(3)

at=131sin(2π×1.953t+2.718)+119.2×sin(2π×5.127t+2.441)

(4)

1.2.3参考理想方程的误差评价

由式(2)～(4)建立的运动方程，以理想加速度方程at为基准，对测量数据进行误差分析[5],用理想加速度方程和经过剔除无效值之后的3组测量数据分别进行拟合，得到:

(5)

2)平均相对误差：

(6)

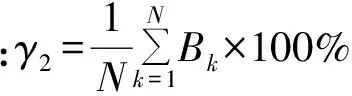
(7)

合格率表示以相对偏差在25%内为合格点，采样时段内的合格点数占总采样点数的比重,其中:

4)加速度总面积：S=∑ai

(8)

式(8)中，S为加速度总面积，ai为提出无效值之后各采样时刻的加速度测量数据，由于时域上3组采样间隔等值，故将时间简化为标幺值1。加速度总面积物理意义为一个运动过程结束后的摆动速度，根据运动结束后停止摆动的情景分析，理想情况下S=0。通过对式(5)～(8)的计算，得到误差评价表如表2所示。

从表2中可看出，A组数据与理想加速度偏差较小，B组、C组数据与理想加速度偏差较大，且存在明显的误差。

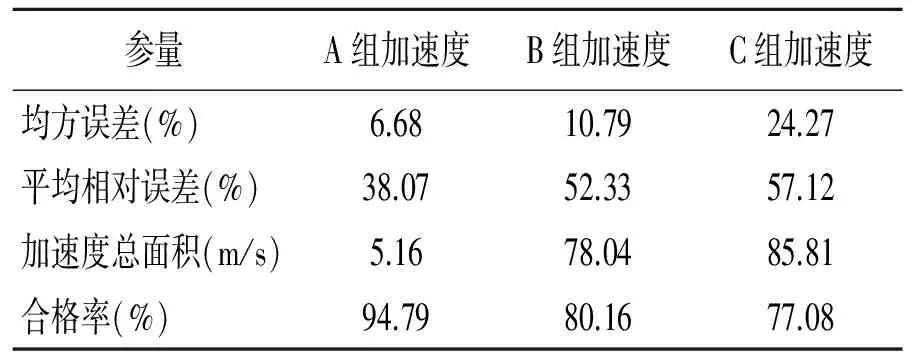
表2 误差评价表

2 基于加速度零补偿和经验模态分解对误差的消除

2.1零加速度补偿法消除系统误差

2.1.1零加速度补偿法的基本原理

零加速度补偿法是对每一个数据进行补偿，促使误差在积分中的累积效应得到减弱。零加速度补偿原理图如图4所示，从图4中可以看出，由于误差的存在，发现加速面积不等于减速面积，通过进行补偿，使坐标轴上移(变为虚线段部分)。

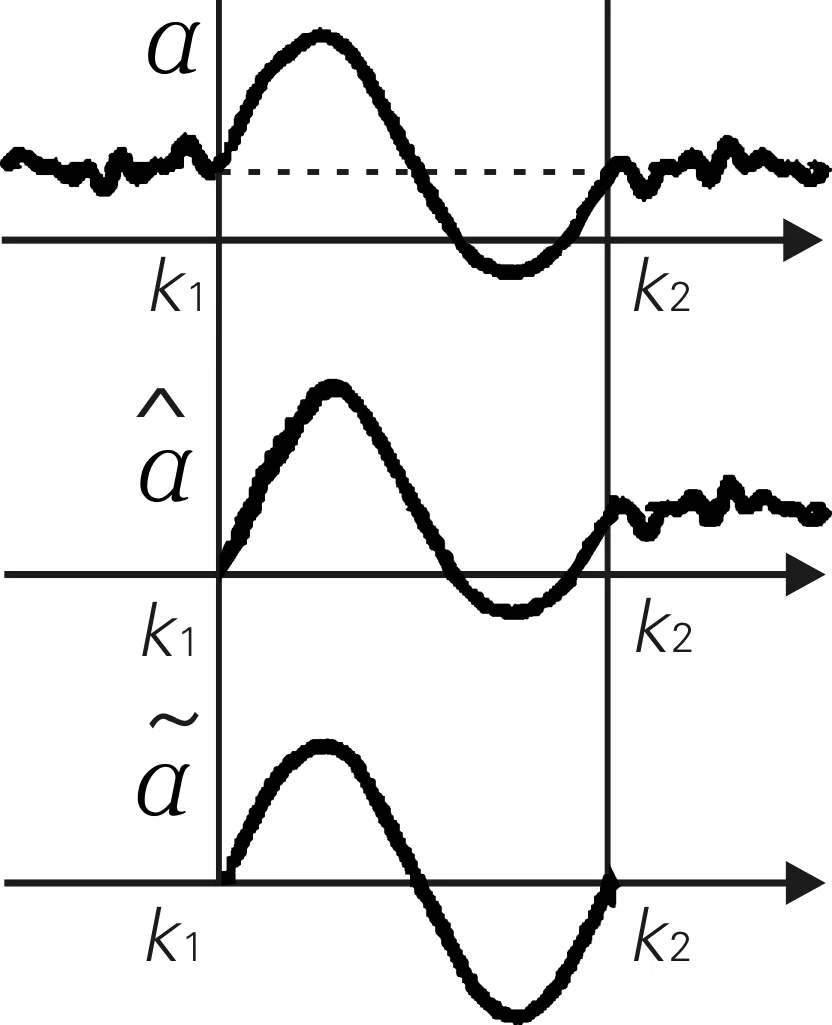
图4 零加速度补偿原理图

具体过程如下：

(9)

(10)

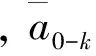
单方向运动(A组)过程简单、误差较小，所以不用补偿；而对B、C组过程，由于系统误差的存在，经过加速和减速过程后，速度并没有变为零，为了消除系统误差，采取零加速度补偿，使加速面积等于减速面积，以符合基本物理规律。

2.1.2零加速度补偿法的处理效果

用matlab编程后得到B组和C组的速度、位移修正前和修正后的波形,分别如图5～8所示。

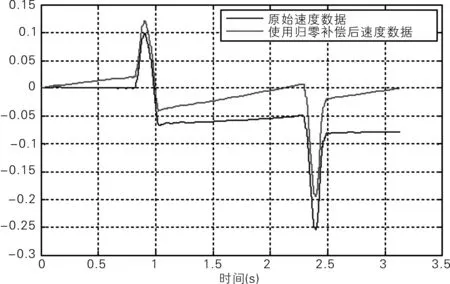
图5 B组速度对比

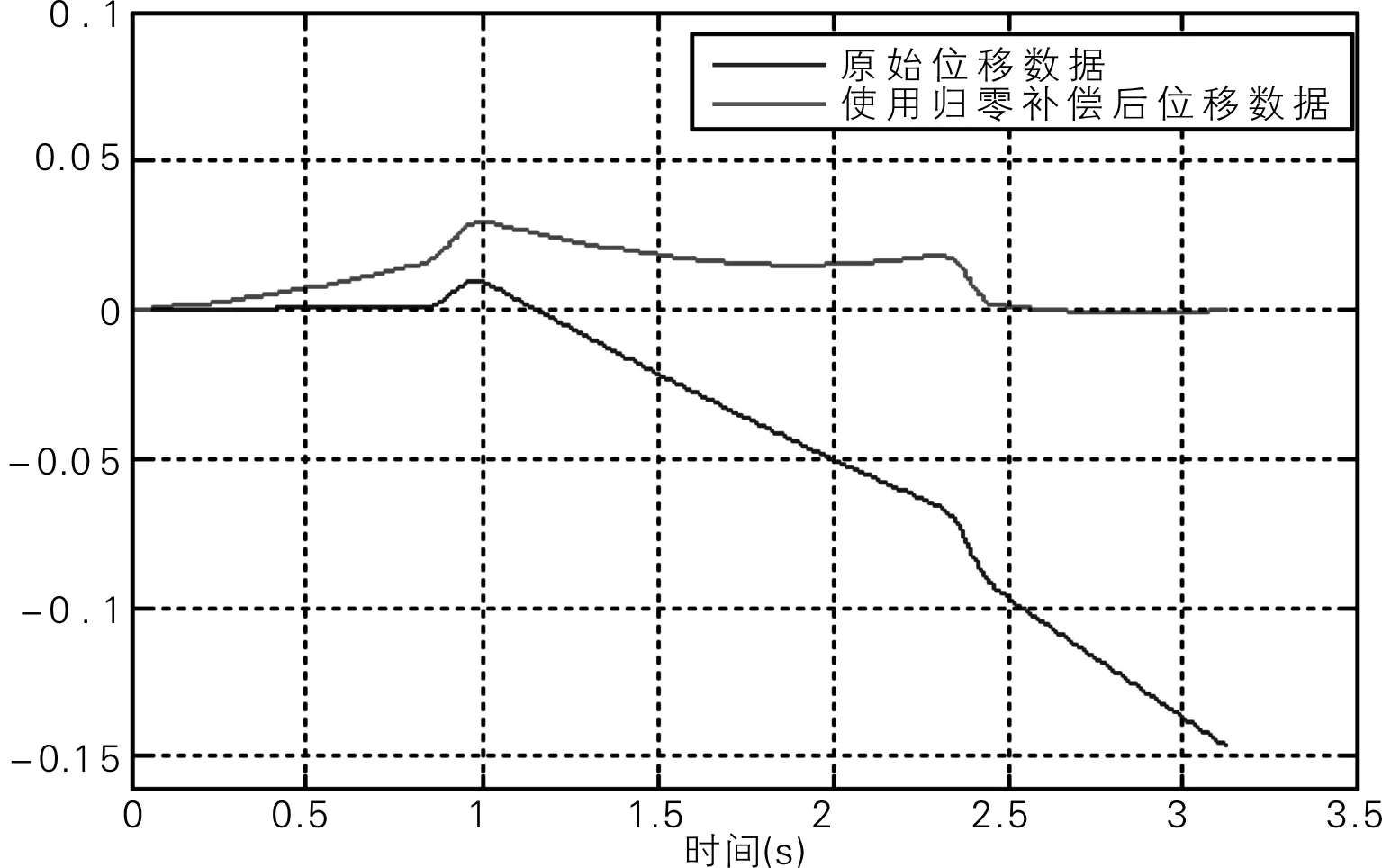
图6 B组位移对比

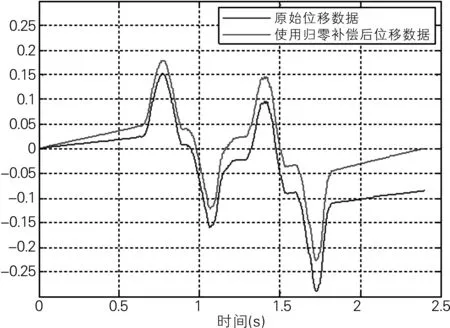
图7 C组速度对比

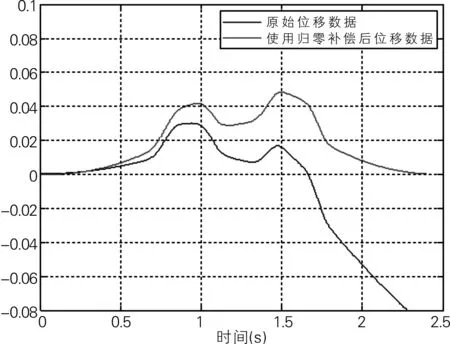
图8 C组位移对比

通过对图5～8归零补偿前后速度、位移的比较可知：通过零值补偿能够明显消除系统误差，得到的波形与实际吻合。以B组的速度为例，在未补偿前，经过一个加速、减速周期后，速度都会偏离零值，而采用归零补偿后，速度的偏移得到极大的削减。

2.2 EMD消除随机误差

2.2.1 EMD滤波的原理

EMD算法是近年来发展起来的一种新型的自适应信号时频分析方法，它依据信号自身的特点，自主地抽取信号内在的固有模态函数，是一种适用于分析非线性、非平稳信号的方法。该方法被认为是对以线性平稳假设为基础的傅立叶分析和小波变换等传统时频分析方法的重大突破[7]。EMD滤波具体方法如下：

找出信号x(t)全部极大点和极小点, 将它们分别拟合为原序列的上、下包络线,将原数据序列减去包络线对应坐标均值m1可得到一个新数据序列c。一般c1不是平稳数据序列,需判定并重复以上过程n次,得到的m趋向零。

用x(t) 减去c1得到的新序列去掉高频成分,重复上段,得到一系列cn和最后一个不可分解的序列rn,rn就代表x(t) 的均值或趋势项。这样,原序列x(t) 可表示为固有模态函数分量和一个残余项的和,即:

(11)

假若信号x(t)是一个含噪声的一维信号, 可用如下形式表示:

x(t)=f(t)+εe(t) (t=0,1,2,…,n-1)

(12)

式(12)中 ,x(t)为含噪信号，f(t) 为有用信号，e(t) 为噪声信号。e(t) 通常表现为高频信号, 而实际工程中f(t) 通常为低频信号。对于电机振动加速度信号，随机误差主要表现为高频噪声，滤除随机误差即对信号x(t) 消噪，也就是要去除e(t)[8]。

2.2.2滤除随机误差后的加速度波形

滤波后的加速度波形如图9所示。观察图9可以发现，滤除随机误差后的加速度波形清晰，接近理论情况。通过比较滤波后和滤波前加速度的波形，很清楚地看到滤波后波形上的噪音部分已被消除，波形的包络线十分清晰，且波形与理论情况十分接近，因此，认为用EMD消除随机误差是可行的，且可靠性较高。

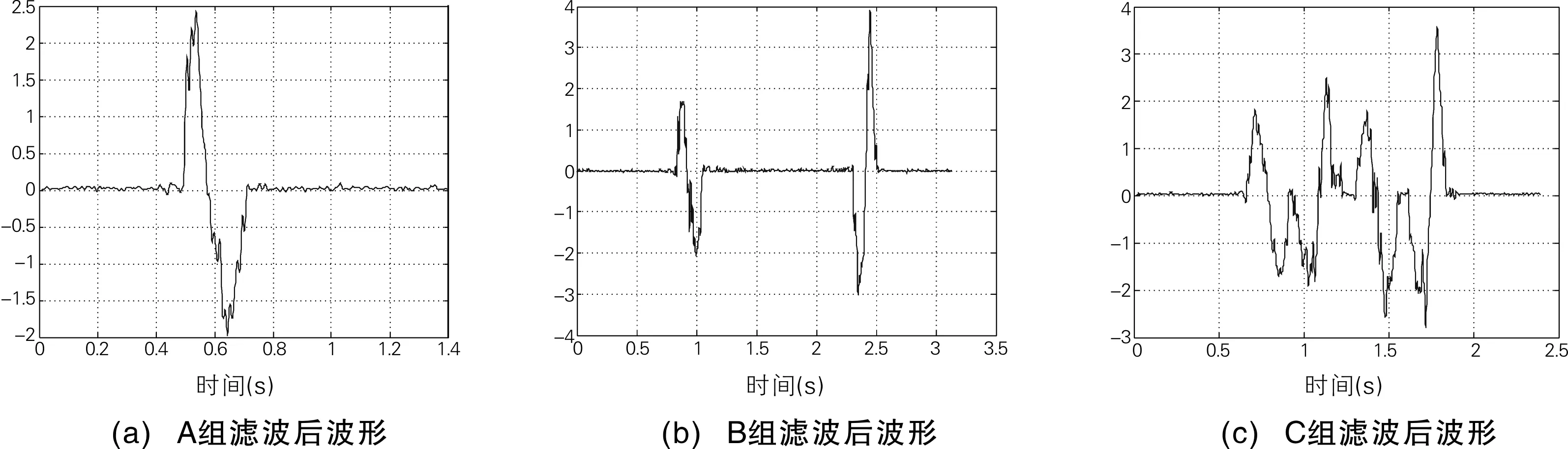
图9 滤波后的加速度波形

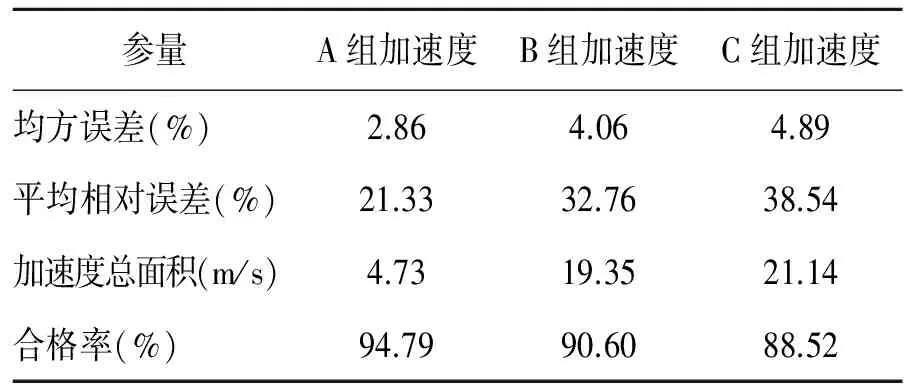
表3 改进算法后的误差评价

2.3改进算法得到结果的误差评价

用基于零补偿和EMD的改进算法得到的结果，重新剔除无效值并再次进行误差评价，改进算法后的误差评价如表3所示。

对比表2、表3可知，A组的误差指标变化不大，但是B、C组发生极大的变化，误差被较好地消除。因此基于零补偿和EMD的改进算法能够有效地消除误差，提高了测量数值和积分结果的准确性。

3 结论

本文通过误差分析，剔除了测量加速度数据的无效值，对剔除后的数据进行了频谱分析，得到系统误差和随机误差，求出了理想变化曲线。针对这2种误差，采用基于零补偿和EMD去噪的算法改进，展示了改进后得到的速度和位移波形，并对采取误差消除前后的加速度波形进行了比较与评价，证明该改进算法能够有效地降低测量中的误差。

[1] 李广军，金炜东.列车横向加速度传感器的误差补偿[J].计算机工程与应用，2012，48(5)：15-17.

[2] 周英杰.加速度测试积分位移算法及其应用研究[D].重庆:重庆大学，2013.

[3] 李晓龙，张志洲，佘龙华，等.高速磁悬浮列车悬浮控制中加速度信号数字滤波算法研究[J].机车电传动，2009(1):39-42.

[4] 刘牮，张辉，雷龙,等.加速度数据的采集及分析[J].信息技术，2013(12)：110-116.

[5] 宋薇.大规模风电场超短期风电功率预测的误差分析与评价[D].吉林:东北电力大学，2013.

[6] 徐时伟.用于空中手写的加速度传感器积累误差消除技术研究[D].杭州:浙江大学，2012.

[7] 陈隽,徐幼麟.经验模式分解在信号趋势项提取中的应用[J].振动、测试与诊断，2005,25(2):101-104.

[8] 赵宝新，张保成,赵鹏飞,等.EMD在非平稳随机信号消除趋势项中的研究与应用[J].机械制造与自动化，2009,38(5)：85-87.

(责任编辑吴鸿霞)

Method of Eliminating Integral Error Based on Zero Compensation and EMD

FengKun1,FengJianlan2*

(1School of Electrical Engineering,Wuhan University,Wuhan Hubei 430072;2Hubei Polytechnic University,Huangshi Hubei 435003)

For seeking the method of eliminating the acceleration integral error,this paper uses the frequency analysis on the measured data and get the error frequency and ideal acceleration curve, then process measured data based on the zero compensation and Empirical Mode Decomposition(EMD),correct and evaluate the error.The conclusion proves that this method can eliminate the error in integral.

acceleration sensor;spectral analysis;error evaluation;EMD

2014-03-31

冯锟(1993— ),男,武汉大学2011级电气工程与自动化专业本科生。

*通讯作者：冯建兰(1959— ),女，教授，硕士，研究方向：自动控制。

10.3969/j.issn.2095-4565.2014.04.006

TM301.4

A

2095-4565(2014)04-0020-05