Hierarchical Combination Reliability Modeling Method for Fault Tolerant Sensor System*

YUAN Liaoyuan，ZHANG Weiguo，LIU Zhijun

(School of Automation，Northwestern Polytechnical University，Xi’an 710072，China)

Hierarchical Combination Reliability Modeling Method for Fault Tolerant Sensor System*

YUAN Liaoyuan，ZHANG Weiguo*，LIU Zhijun

(School of Automation，Northwestern Polytechnical University，Xi’an 710072，China)

According to the architecture feature of the fault tolerant sensor system，a hierarchical combination reliability modeling method based on the dynamic fault tree analysis and the Markov process was proposed with the combination of the advantages of multiple modeling approaches.Temporal operators were applied to represent the sequential logic，and the analytic formula for the failure probability of the top event was derived.The failure detection and isolation behavior was modeled by the Markov process.The resultant model was compared to the perfect fault coverage model.The impact of the parameters on the system reliability was evaluated.The simulation results demonstrate the modeling method is feasible，efficient and more accurate.

sensor application;reliability modeling;hierarchical combination method;dynamic fault tree;Markov process;FDI parameters

传感器系统是飞行控制系统的重要组成部分。传感器系统可靠性对整个飞控系统的可靠性有着重要的影响。通常，民机飞行关键信息(姿态、速度以及高度)测量功能的最大失效概率要求小于10－9每飞行小时。为了满足高可靠性要求，传感器系统设计采用多余度容错体系结构。复杂余度结构的引入以及故障诊断与隔离容错算法的应用，为可靠性建模分析带来了挑战［1－2］。

研究人员对于余度容错系统的可靠性进行了深入的研究:文献［3］针对非相似容错飞控计算机系统，采用动态故障树建立可靠性模型，使用动态故障树转换为马尔可夫模型的方法进行可靠度计算;文献［4］讨论了应用马尔可夫模型方法分析容错导航系统可靠性的化简问题，依据马尔可夫模型求解得到的组件可靠性模型，采用组合分析的方法求解得到系统可靠性模型，简化了分析过程并减少了计算量;而文献［5］中则采用广义随机Petri网方法对Boeing 777飞机的主飞行计算机系统进行了可靠性建模。

综合国内外相关文献，高可靠性要求的容错系统的分析通常基于某种单独的可靠性建模方法，主要存在的问题包括以下两点:(1)系统模型的状态数量较多，计算求解较为困难，如基于状态的Petri网模型以及马尔可夫模型均会受到状态空间爆炸问题的制约;(2)建模中失效概率分布为指数的通用假设不能成立，这一点制约了经典时间齐次马尔可夫方法的应用［6－7］。

基于以上的介绍与分析，本文以民机中广泛应用的容错传感器系统为研究对象，采用分层组合建模的方法解决状态量较多带来的计算求解困难，同时引入基于代数模型的动态故障树建模方法，适用于任意寿命分布类型的元件建模。

1 容错传感器系统的架构［8］

霍尼韦尔研发的大气数据惯性基准系统(ADIRS)是空中客车系列、波音系列等大型运输机的标准惯性基准系统，是传感器系统的主要组成部分。ADIRS主要包括大气数据惯性基准单元ADIRU(Air Data Inertial Reference Unit)、辅助姿态大气数据基准单元SAARU(Secondary Attitude and Air Data Reference Unit)。

ADIRU是一个六余度斜置配置，容错捷联惯性基准单元，采用了六余度激光陀螺，六余度加速度计、四余度处理器以及相应的输入/输出组件和电源组件，提供FO/FO/FS等级的容错能力。表1为ADIRU中各容错组件的监控方法和实现监控的所需的最小余度数。

表1 ADIRU中余度管理方法与余度数关系

SAARU采用了与ADIRU非相似的设计方法。陀螺和加速度计采用了四余度设计，处理器为两余度，I/O模块为三余度设计。SAARU的容错能力为故障安全。在ADIRU正常工作的情况下，飞行控制计算机系统以及主飞行显示系统的飞行信息均由ADIRU提供。而当ADIRU失效时，SAARU负责提供相应备用的飞行信息。

2 分层组合可靠性建模分析

2.1 方法概述

系统分析的分层/组合方法在以下两种情况下具有高效率的分析与计算能力:(1)如果系统各部分间的动态过程相互独立，不存在相互作用，可以研究各部分内部的相互作用;(2)在不涉及各部分内部的相互作用的前提下，对各部分间的相互作用进行分析。

基于上述的两点有效性准则，结合系统结构以及表1所示的系统各组件的余度管理方法，容错传感器系统的分层组合建模如图1所示。

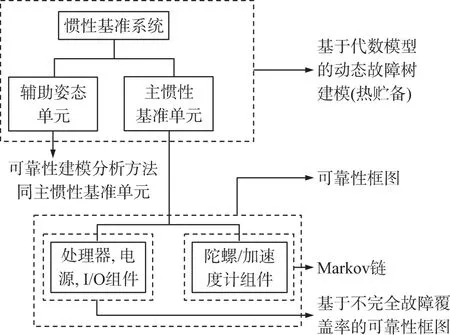
图1 分层组合建模可靠性建模示意图

具体的分析如下:

(1)陀螺和加速度计组件余度等级较高，采用广义似然比检验的方法进行故障检测隔离以及系统重构。为了描述组件的复杂动态行为，采用基于状态的马尔可夫模型进行建模分析。

(2)处理器、电源以及I/O组件的可靠性建模则考虑故障监控覆盖率因素的影响，采用了不完全故障覆盖率的可靠性框图方法［9－10］。而主惯性基准单元与辅助姿态单元中各容错组件间故障相互独立，不存在相互作用，因此采用可靠性框图方法，所建立的模型简单，求解效率高。

(3)主惯性基准单元ADIRU与辅助姿态单元SAARU故障逻辑关系满足热贮备关系，而两单元失效概率分布函数不满足指数分布的条件，因而无法采用将动态故障树等价转化为马尔可夫链的常规求解方法。针对此问题，本文引入基于代数模型的建模分析方法进行解决。

2.2 基于代数模型动态故障树的可靠性建模

动态故障树方法通过引入动态逻辑门，如优先与门、功能依赖门、贮备门，反映系统故障发生时序关系等动态相关特性。动态逻辑门的建模与分析是动态故障树方法的关键，常见的处理方法包括马尔可夫法、计数过程法、代数模型法等。

相对于马尔可夫法以及计数过程法，代数模型法的应用限制更少，适用于所有故障——时间分布类型的元件建模与分析，且表述计算更为精简［11～14］。因而，本文采用该方法对系统两测量单元组件进行建模与分析。

2.2.1 基于时间算子的定性分析

代数模型方法中引入时间算子描述时序顺序。考虑两输入事件温储备门，热储备门可以视为温储备门的一种特殊情况进行推导。温储备门的代数模型表达式为:

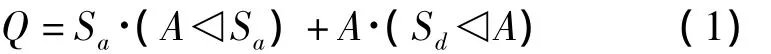
其中，时间算子◁表示“在……之前发生但并不包含”。Q为代表顶事件发生的逻辑变量。A为代表主要元件失效的逻辑变量。Sa为代表贮备事件S在活跃状态下失效的逻辑变量，Sd为代表贮备事件S在休眠状态下失效的逻辑变量。

由式(1)可见，顶事件Q发生包括两种模式:A在S之前发生——Sa·(A◁Sa)，储备元件故障前处于活跃状态;或者S在A之前发生——A·(Sd◁A)，储备元件故障前处于休眠状态。由于储备元件不可能同时处于活跃或休眠两种状态，可知两种故障模式相互独立，即事件Sa·(A◁Sa)与A·(Sd◁A)的交集为空。

2.2.2 定量概率计算公式的推导

本小节基于文献［12］中的方法对上一小节所建立的代数模型进行定量概率公式的推导。顶事件Q的两种故障模式相互独立，所以有

分别考虑两种故障模式的定量概率计算如下:

首先考虑A·(Sd◁A)所代表的故障模式——贮备元件先于主要元件故障。由于贮备元件在休眠状态下的故障与主要元件工作状态下的故障相互独立，所以故障概率计算如下:

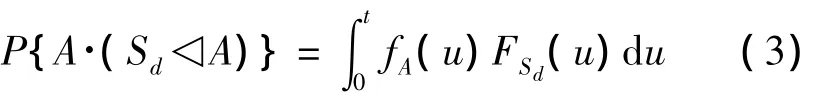
其中，fA(·)代表主要元件失效概率密度函数，FSd(·)代表贮备元件在休眠状态下的累积失效概率。

考虑Sa·(A◁Sa)所代表的故障模式——主要元件先于贮备元件故障。由于故障时序的约束，贮备元件在工作状态下的失效累积分布函数FBa(·)和概率密度函数fBa(·)均与主要元件的失效累积分布函数相关，因此该模式下的故障概率计算不能使用式(3)的形式。具体的推导过程如下所示。

设TA和TSa分别为主要元件A和工作状态下储备元件S的故障时间。

其中，I为指示函数，满足

由全期望公式E［X］=E［E［X|Y］］可得，

其中，RSd(·)为贮备元件休眠状态下的可靠度函数，满足RSd(x)=1－FSd(x)。

将式(3)和式(6)代入式(2)即可得到温储备门的定量概率计算公式:

当贮备元件在工作状态和储备状态下的失效率相同时，即贮备元件失效累积概率密度和累积分布函数相同(fSd(x)=fSa(x)=fS(x))时，即可由式(7)可以推导得到热储备门的概率计算公式:

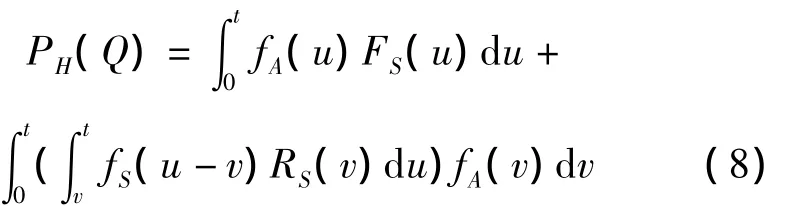
2.3 陀螺/加速度计组件的建模

容错系统的可靠性与系统所采用的故障检测与隔离方法是相关的。广义似然比检验中的相关概率包括:误检概率PF、漏检概率PM、正确检测概率PD、正确隔离概率PI。

综合考虑了故障漏检概率和误检概率对可靠性的影响，忽略同一检测周期内两次或两次以上故障的概率，采用Markov链描述主惯性基准单元中陀螺/加速度计组件余度结构和容错动态过程。陀螺/加速度组件对应的Markov链如图2所示。状态定义以及状态转移如表2所示。由于广义似然比检测需要至少四元素实现一致性监测，因此当陀螺/加速度组件中少于4个元件正常工作时，即解除测量单元的连接，从而实现故障安全的容错能力。

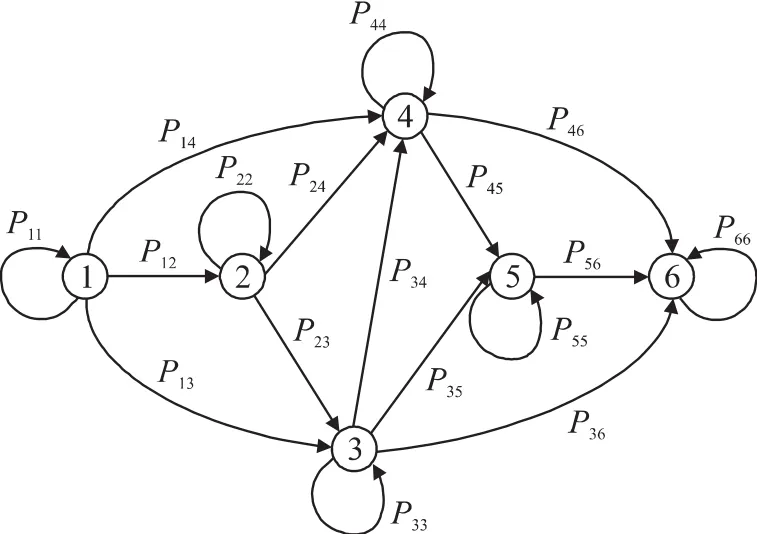
图2 陀螺/加速度组件对应的Markov链

表2 陀螺/加速度组件工作状态以及状态转移的定义

状态转移概率状态变量用X表示，第k时刻的状态用X(k)表示，Pij=P(X(k)=j|X(k－1)=i)表示状态i到状态j一步转移概率，由表2中的状态转移定义即可计算得到。

Pij=0，对于其他的i，j

由离散时间离散状态齐次马尔可夫过程的状态转移可知:

其中，π(k)=π1(k)，…，πm(k))T为系统第k步的m个状态概率向量，系统初始时刻的状态概率向量π(0)通常给定为已知。则t时刻系统可靠度为:

其中，W为系统正常工作状态集合，W={1，3，5}。Δt为容错系统故障检测周期。由故障检测频率为50 Hz可得Δt=0.02 s。

2.4 处理器、电源、输入/输出组件的可靠性建模

由表1可知，处理器、电源、I/O组件均可由表决系统进行描述。而考虑余度管理方法对可靠度的影响，采用不完全故障覆盖率模型进行可靠性的建模。

表决系统的可靠度计算公式为:

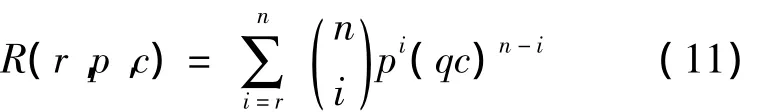
其中，n为各组件中的余度元件数，r为组件正常工作所要求的最小元件数，p、q分别为余度元件的可靠度和不可靠度，c为故障覆盖率。由式(11)即可计算得到处理器、电源、I/O组件的可靠度。

由以上可靠性建模分析方法，分别可以计算得到主惯性基准单元的陀螺组件、加速度计组件、电源组件、处理器组件以及I/O组件的可靠度分别为。各组件之间满足串联逻辑关

系。主惯性基准系统可靠度计算公式如下:

可能为流量计内进入脏污，导致浮子抖动或卡顿，此时需对流量计进行清洗。对于金属材质的浮子，可按顺序将水、无水乙醇、丙酮、乙醚注入流量计内将赃物洗净，对于塑料材质浮子，则可用洗洁精、水、无水乙醚进行清洗。待管内溶剂干燥后再装回原来位置。

辅助姿态单元在余度数上采用了非相似的设计方法，而余度管理方法与主惯性基准单元相同。可靠性建模与分析不再赘述，辅助姿态单元可靠度函数为RS。

2.5 系统可靠性的融合计算

系统可靠性的融合计算［15－16］的关键在于代数模型方法的运用，将动态逻辑门的定量概率计算与Markov链的求解结果结合在一起。图3所示为顶事件所包括的动态逻辑门。动态逻辑门的两输入事件——“主惯性基准单元失效”和“辅助姿态单元失效”对应的可靠度函数RA、RS即通过基于Markov链的建模方法求解得到。

图3 顶事件动态逻辑门

而由于Markov链是对离散时间离散状态转移的描述。可靠度函数RA、RS的具体数学表达式表明，输入事件对应的失效分布为不符合指数分布的离散分布形式，常用的马尔可夫过程法不再适用于动态逻辑门的分析处理。而代数模型方法通过对式(6)的离散形式进行推导，不受分布的限制，最终得到系统可靠度的表达式，求解过程如下:

主惯性基准单元与辅助姿态单元的分布律为:

系统的可靠度函数为:

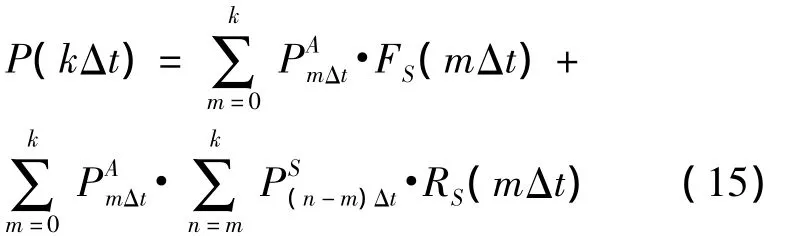
其中，kΔt为系统工作时间，Δt为故障检测隔离周期。F(t)=1－R(t)为两单元的累积失效概率。

3 仿真与分析

陀螺和加速度计组件具有复杂的余度结构以及余度管理方法，作为系统底层元件寿命分布满足指数分布的条件，符合Markov链动态描述性能较好同时对元件分布有限制的特性。基于各个组件计算得到的两单元具有故障时序性的特点，同时不满足特定的指数分布，采用基于代数模型的动态故障树方法，最终推导得到系统的分层组合可靠性模型。通过与传统完全故障覆盖模型进行仿真计算比较，分析容错系统的设计参数对系统可靠性的影响，分层组合模型的准确性与合理性得到体现。

3.1 组合建模模型与完全故障覆盖模型的比较

图4两类模型的可靠性仿真计算结果比较

图4 所示为两种模型可靠度的对比。由图可知，两种模型计算得到的失效概率均小于10－9/飞行小时，满足可靠度定量概率要求。分层组合模型的计算结果比完全故障覆盖模型高出约3个数量级。由仿真条件设置可知，可靠度数量级上的差距是由故障检测相关概率所引起的。此外，在工程实际的可靠性评估中，要求被评估对象的失效概率小于某一给定指标时，通常采用失效概率较高的保守模型，因此分层组合模型在这点上优于完全故障覆盖模型。3.2小节中将对容错系统设计参数的影响进行进一步的分析，体现分层组合模型的准确合理。

3.2 相关概率对系统可靠度的影响分析

本节通过分析系统设计参数——虚警概率、漏检概率以及元件失效率对系统可靠性的影响，体现分层组合模型的准确与合理。在分析一种参数的作用时，其他参数均固定不变。

图5所示为陀螺元件失效率对系统故障概率的影响。系统元件的失效率是完全故障覆盖模型所主要考虑的因素。由图可知，与完全故障覆盖模型相比，分层组合模型同样能够反映元件失效率的影响，并得出关于元件失效率影响的结论:当一类元件的失效率远远大于其他元件时，该元件对系统可靠性起决定性的影响。而失效率较低的元件可靠性的提高对系统可靠性的影响较小。

图5 陀螺失效率与系统故障概率的关系

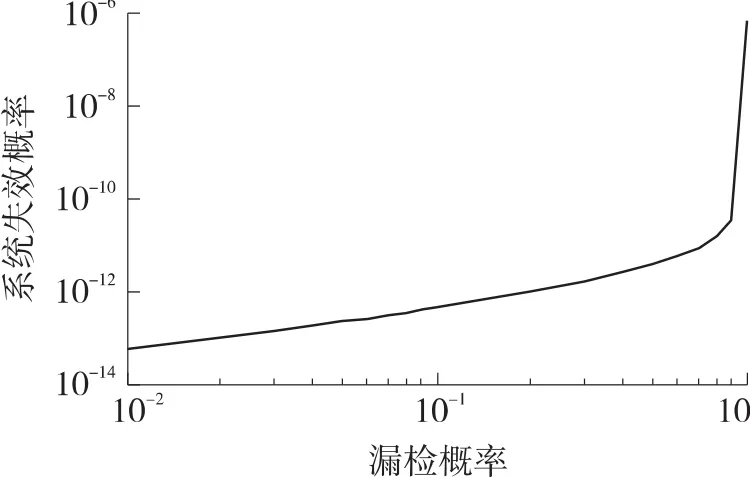
图6漏检概率与系统故障概率的关系

图6 给出了系统故障概率与漏检概率的关系。漏检概率描述了系统故障后未得到正确检测的概率。漏检概率直接影响系统的安全可靠性。实际飞行控制系统中不同故障监控方法的漏检概率相差很大，如基于表决的比较监控方法与自监控方法的漏检概率相差近1个数量级。通常故障诊断方法的漏检概率的变化范围为0.01～0.20，由图可得，当漏检概率由0.01增大到0.20时，系统失效概率增大了约2个数量级，由此可见，故障诊断中的漏检概率在可靠性建模分析中不能忽略。而在系统可靠性设计中，相对于提升元器件可靠度所带来的巨大成本代价，采用检测概率更高的故障检测与隔离算法对系统可靠度的提升效果更为明显。

图7所示为误检概率对系统可靠性的影响。误检概率定义为系统未发生故障，诊断方法进行检测隔离的概率。系统失效概率在误检概率10－8～10－5的变化范围内快速增大，表明误检概率与漏检概率同样是可靠性建模中不可忽略的重要因素。

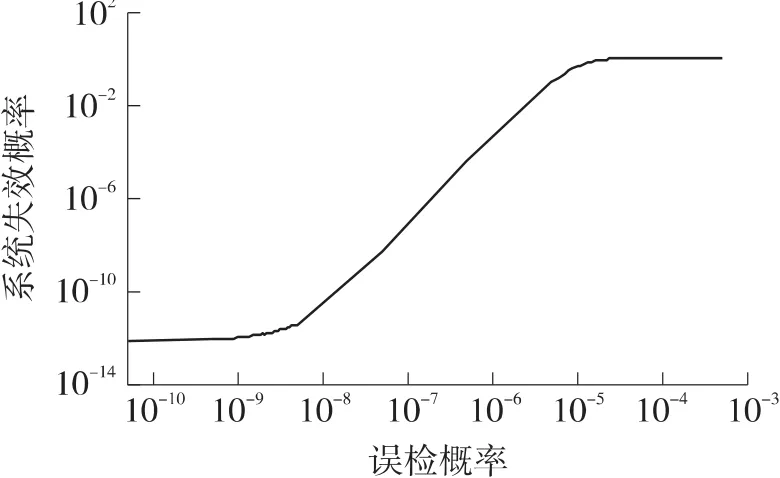
图7 误检概率与系统故障概率的关系

值得注意的是，误检概率与故障检测阈值的设置直接相关。例如第1节中所给Honeywell容错传感器系统可靠性设计指标规定:故障检测阈值设置需要保证飞行控制输出信号的误检概率不大于10－5/h，导航输出信号的误检概率不大于10－3/h。根据给定指标，故障检测周期Δt内的误检概率可以根据公式PfΔT=1－(1－Pf)Δt/3600计算得到。而系统误检概率与故障检测阈值之间满足公式:

其中TD即为故障检测阈值。由此可见，误检概率是联系可靠性设计与诊断方法设计的重要品质因数。

综上所述，分层组合模型合理准确地考虑了容错系统可靠性相关的多个因素，优于完全故障覆盖模型，同时与诊断方法设计相联系，有助于容错系统的综合设计。

4 结论

本文运用代数模型动态故障树不局限于部件寿命分布类型的特性，利用马尔可夫过程对动态过程较强的表述能力，对容错传感器系统进行了可靠性的建模与分析。仿真结果表明系统可靠度是各设计参数的函数。因此，文中所提出的方法不但可以应用于不同余度结构设计方案的比较，而且可以对容错系统设计参数的确定进行优化，对当前大型民机飞行控制系统设计［17－18］具有一定的参考借鉴意义。

［1］姚一平，李沛琼.可靠性及余度技术［M］.航空工业出版社，1991:181－218.

［2］Li H，Zhao Q，Yang Z.Reliability Modeling of Fault Tolerant Control Systems［J］.International Journal of Applied Mathematics and Computer Science，2007，17(4):491－504.

［3］安金霞，朱纪洪，王国庆，等.多余度飞控计算机系统分级组合可靠性建模方法［J］.航空学报，2010，31(2):301－309.

［4］王社伟，张洪钺.容错导航系统可靠性评估的一种简化方法［J］.系统工程与电子技术，2000，22(10):82－85.

［5］秦旭东，陈宗基.基于Petri网的非相似余度飞控计算机可靠性分析［J］.控制与决策，2005，20(10):1173－1176.

［6］孙晓哲，李卫琪，陈宗基.飞控计算机系统分层混合可靠性建模方法［J］.上海交通大学学报，2011，45(2):277－283.

［7］张竞凯，章卫国，刘小雄，等.基于贮备门DFT的飞控系统可靠性分析方法［J］.计算机测量与控制，2013，21(001):142－145.

［8］McClary C R，Walborn J R.Fault-Tolerant Air Data Inertial Reference System Development Results［C］//IEEE Position Location and Navigation Symposium，1994:31－36.

［9］Xiong X，Zhang P.Reliability Analysis of Flight Control System for Large Civil Aircraft with Imperfect Fault Coverage Model［C］// IEEE Conference on Prognostics and System Health Management (PHM)，2012:1－5.

［10］Myers A，Rauzy A.Efficient Reliability Assessment of Redundant Systems Subject to Imperfect Fault Coverage Using Binary Decision Diagrams［J］.IEEE Transactions on Reliability，2008，57(2): 336－348.

［11］Merle G，Roussel J M，Lesage J J，et al.Algebraic Expression of the Structure Function of a Subclass of Dynamic Fault Trees［C］//Proceedings of the 2nd IFAC Workshop on Dependable Control of Discrete Systems(DCDS’09)，2009:129－134.

［12］张竞凯，章卫国，刘小雄，等.基于代数模型的飞控计算机可靠性分析方法［J］.北京航空航天大学学报，2014(2):262－267.

［13］Merle G，Roussel J M，Lesage J J，et al.Analytical Calculation of Failure Probabilities in Dynamic Fault Trees Including Spare Gates［C］//European Safety and Reliability Conference，2010.

［14］Tannous O，Xing L，Bechta Dugan J.Reliability Analysis of Warm Standby Systems Using Sequential BDD［C］//Reliability and Maintainability Symposium(RAMS)2011 Proceedings-Annual IEEE，2011:1－7.

［15］杨佳，宫峰勋.基于贴近度的多传感器一致可靠性融合方法［J］.传感技术学报，2010，23(7):984－988.

［16］赵乃卓，孙威.基于冗余方案电磁式漏磁传感器管壁测厚的研究［J］.传感技术学报，2011，24(6):934－936.

［17］秦旭东，陈宗基，李卫琪.大型民机的非相似余度飞控计算机研究［J］.航空学报，2008，29(3):686－694.

［18］Rehage D，Carl U B，Vahl A.Redundancy Management of Fault Tolerant Aircraft System Architectures-Reliability Synthesis and A-nalysis of Degraded System States［J］.Aerospace Science and Technology，2005，9(4):337－347.

袁燎原(1988－)，男，安徽省亳州人，博士，研究方向为飞行控制系统传感器容错方法与信息融合，yuanliaoyuan @163.com;

章卫国(1956－)，男，安徽南陵人，教授，博导，研究方向为先进飞行控制和智能控制。

容错传感器系统分层组合可靠性建模方法*

袁燎原，章卫国*，刘志君
(西北工业大学自动化学院，西安710072)

根据容错传感器系统的结构特点，结合不同可靠性建模方法的优点，提出了基于动态故障树和马尔可夫过程的分层组合可靠性建模方法。针对系统中包含的贮备事件，引入时间算子定性描述事件的时序特性，并推导了顶事件故障概率的定量计算公式。采用马尔可夫过程对传感器故障检测隔离进行动态建模。通过仿真比较所得模型与传统完全故障覆盖模型，分析了元件失效率、误检率等参数对系统可靠性的影响。由结果可得，该建模方法可行且更为精确。

传感器应用;可靠性建模;分层组合方法;动态故障树;马尔可夫过程;FDI参数

TP212.9

A

1004－1699(2014)04－0529－07

2013－11－28修改日期:2014－03－19

C:0240J;0250

10.3969/j.issn.1004－1699.2014.04.020

项目来源:国家973计划项目(20126131890302);陕西省自然科学基金项目(2013JQ8026)