Planar Electromagnetic Positioning System*

BAO Jianmeng，HU Chao，LIN Weixing，WANG Wenhu，WANG Tao

(1.Ningbo University，Ningbo 315211，China;2.Ningbo Institute of Technology，Zhejiang University，Ningbo Zhejiang 315100，China)

Planar Electromagnetic Positioning System*

BAO Jianmeng1，2，HU Chao2*，LIN Weixing1，WANG Wenhu1，2，WANG Tao1

(1.Ningbo University，Ningbo 315211，China;2.Ningbo Institute of Technology，Zhejiang University，Ningbo Zhejiang 315100，China)

The coil carrying on current is often used as electromagnetic positioning instrument.It can be used to track moving robot or other objects in real-time.In the system，the magnetic field model around the emitting coil，the signal generating and acquisition circuits，and the localization algorithm directly affects the positioning accuracy of the system.The magnetic dipole model is adopted for positioning calculations.In the case for its moving in the plane，a positioning system was designed based on embedded system ARM(STM32).To get the exact position，it solves the equation with an analytic algorithm for the system with a single transmitting coil and three receiving coils.The moving objects can be located precisely within the range of several meters between the transmitter and the receivers.From the simulation and experimental results，we can observe that the average error is lower than 10 cm.This accuracy is satisfactory for most application.

electromagnetic positioning;planar tracking;magnetic dipole;analytic algorithm;embedded system

磁定位技术主要包括静磁跟踪技术［1－4］和电磁跟踪技术［5－6］。两者都是通过计算磁场强度的方法来得到位置与姿态信息。要得到磁场强度的大小首先要确定磁场的分布状况。磁场分布模型用精确的数学表达式表示是比较复杂的，通常采用简化了的磁偶极子模型来表示磁场的分布，也有采用方形线圈模型［7］。电磁定位系统中常使用缠绕成圆形的线圈。在这种系统中，作为发射器的源线圈被放置在特定的位置上，这些位置的空间坐标已知。通过交流电的激励，源线圈在其自身周围产生磁场。此时，周围的接收线圈中会相应地产生电压信号。电压信号与接收线圈的空间位置与姿态相关，可以用空间位置的函数表示。如果能够得到接收线圈的电压信号，利用源线圈产生的磁场分布模型，我们就可以计算出接收线圈的空间位置参数。因此，磁场分布模型与电压信号的提取［8］对接收线圈空间信息的取得至关重要。

接收线圈可以做成正交的三轴线圈［9］，将接收线圈固定于移动目标(刚体)上，解得接收线圈的空间位置信息也就得到了移动目标的具体位置。移动目标的位置信息除了三维空间的位置参数外，还包括3个姿态参数。确定关于位置信息的方程后，需要采用非线性算法对方程求解，如LM算法［10］。电磁定位技术一般应用在较小空间内的精确定位，如骨科手术机器人［11］。本文针对平面定位，设计一种较大范围内的平面移动目标跟踪定位系统。此系统基于嵌入式系统ARM(STM32)实现，采用解析法来定位离信号源数米范围内的移动目标。

1 检测原理

令O(a，b，c)为磁偶极子(发射线圈)的圆心位置，H0=(m，n，p)为磁偶极子［12］的单位方向向量，则离磁偶极子圆心距离r处的待测目标点P(x，y，z)磁感应强度B表示为如下式子［13］:

其中，BT=μairIR2/4为常量，μair为空气的磁导率。I为电流大小，R为发射线圈半径，r=(x－a，y－b，z－c)且m2+n2+p2=1。

由式(1)可分解得到目标点P(x，y，z)处磁感应强度B在源坐标系x轴、y轴和z轴上的3个正交磁感应强度分量Bx、By和Bz为［14］:

在求得Bx、By与Bz后可联立多组方程解得目标点的位置参数。

待测目标(接收线圈)经过旋转后，3个互相正交的线圈在旋转后感应到的3个磁感应强度为Bu、Bv和Bw。Bx、By、Bz与Bu、Bv、Bw的关系可通过四元素法［15］或者欧拉角［16］法得到。如文献［13］中所设定，定义旋转角度(α，β，γ)为欧拉角。定义Rot(z，γ)为绕z轴逆时针旋转γ角，Rot(y，β)和Rot(x，α)同理。因此有:

其中R=Rot(z，γ)Rot(y，β)Rot(x，α)。

假设发射信号为正弦信号，那么磁感应强度为B=Bmaxsin(ωt+φ)。在远场情况下，各个接收线圈面积比较小，可认为磁感应强度是相同的。由法拉电磁感应定律得:

E为感应电动势，Φ为磁通量。接收信号与发射信号是频率相同的信号，用接收线圈感应信号的幅值来建立方程，其各个分量为:

其中，Su、Sv和Sw分别为接收线圈的面积，Eumax、Evmax和Ewmax分别为3个正交接收线圈上产生的电压幅值，ω为信号的角频率。由式(2)、式(3)、式(4)、式(5)和式(7)便得到了接收线圈感应电磁信号与目标六自由度信息的方程。实际应用中，测出Eu、Ev和Ew后，一个信标(单轴信号发射器)与一个信号接收器(三轴线圈)可确定3个方程，方程中有6个未知数，需要至少6个方程联立解出。因此，至少要2个发射线圈，才能解出位置与姿态信息。

2 平面定位算法

电磁定位系统在跟踪空间目标时需要至少6个方程才能解出具体位置参数。若使用单轴发射线圈、三轴接收线圈，至少要使用2个发射线圈。实际生活中(如室内)，常将移动目标置于某个平面(如地面)，此时目标的活动范围就局限在一个平面范围内。在平面内跟踪移动目标物体要比在空间进行跟踪简单的多，只需要一个发射线圈就可以进行定位工作。此时定位算法可以化为简单的线性计算。

假设发射线圈中心处于点O(0，0，0)，单位方向向量H0=(0，1，0)，使接收线圈的旋转角度α、β和γ都为0度。此时式(7)可化为:

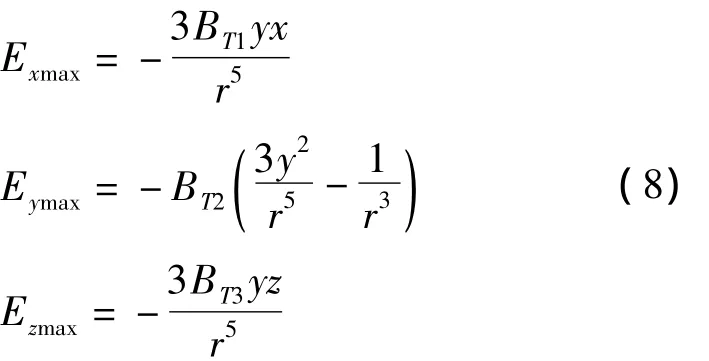
其中，BT1、BT2和BT3大小分别为ωSuBT、ωSvBT和ωSwBT。

假设移动目标(接收线圈)在平面z=C(C≠0)上运动，由式(8)可以化简得到:

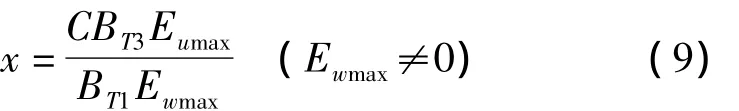
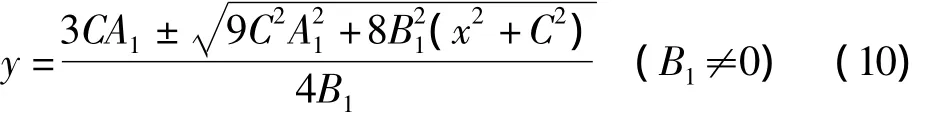
其中，A1=BT3Evmax，B1=BT2Ewmax。由此，便得到了移动目标在平面z=C上的定位方法。

同理，当发射线圈中心处于点O(0，0，0)，单位方向向量H0=(0，0，1)时，可以得到:

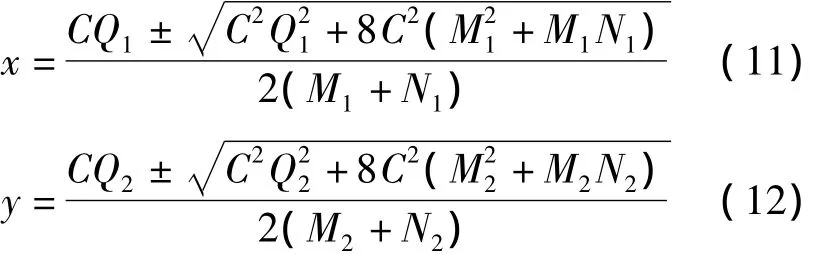
同理，当发射线圈中心处于点O(0，0，0)，单位方向向量H0=(1，0，0)时，可以得到:

其中，A2=BT2Eumax，B2=BT1Ewmax。

3 仿真与实验

3.1 仿真计算

仿真时，取一个圆形信号发射线圈，将其中心置于点O(0，0，0)，使其单位方向向量H0=(0，1，0)。选取平面z=－0.12 m做为运动平面。接收线圈(目标待测点)在平面上做圆周运动，将圆周上101个位置点设为已知定点。首先将已设定点的位置坐标代入式(8)，计算得到3个电压信号Eumax、Evmax和Ewmax。仿真时，此3个电压信号设为已知信号，代入式(9)和式(10)进行反向计算位置参数。真实环境中电压信号会受到噪声信号的干扰。因此，在Matlab中仿真时人为地给电压值加入噪声信号，经过计算，得到不同信噪比(信号与随机噪声幅值之比)下的定位结果如图1所示。取相同点数的曲线形与折线形运动轨迹点，进行仿真跟踪，得到结果如图2与图3所示。

随着噪声的增长，计算得到的位置与设定位置误差增大，且离散性也增大。可以看出，在信噪比为20时，3种形状下已有部分位置误差达到10 cm左右。为此，应该将信噪比控制在20以上。

定义位置平均误差Eaver为:

图2 不同信噪比下曲线设定位置与计算位置对比(单位:m)

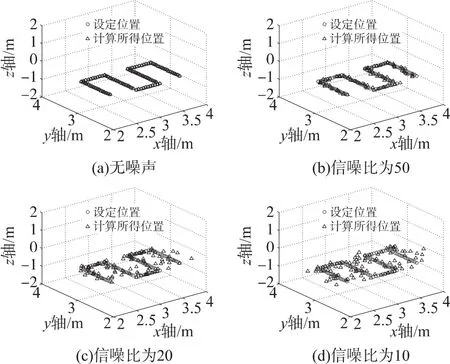
图3 不同信噪比下折线设定位置与计算位置对比(单位:m)

在不同信噪比的仿真情况下，计算得到不同形状位置跟踪的平均误差的大小如表1所示。

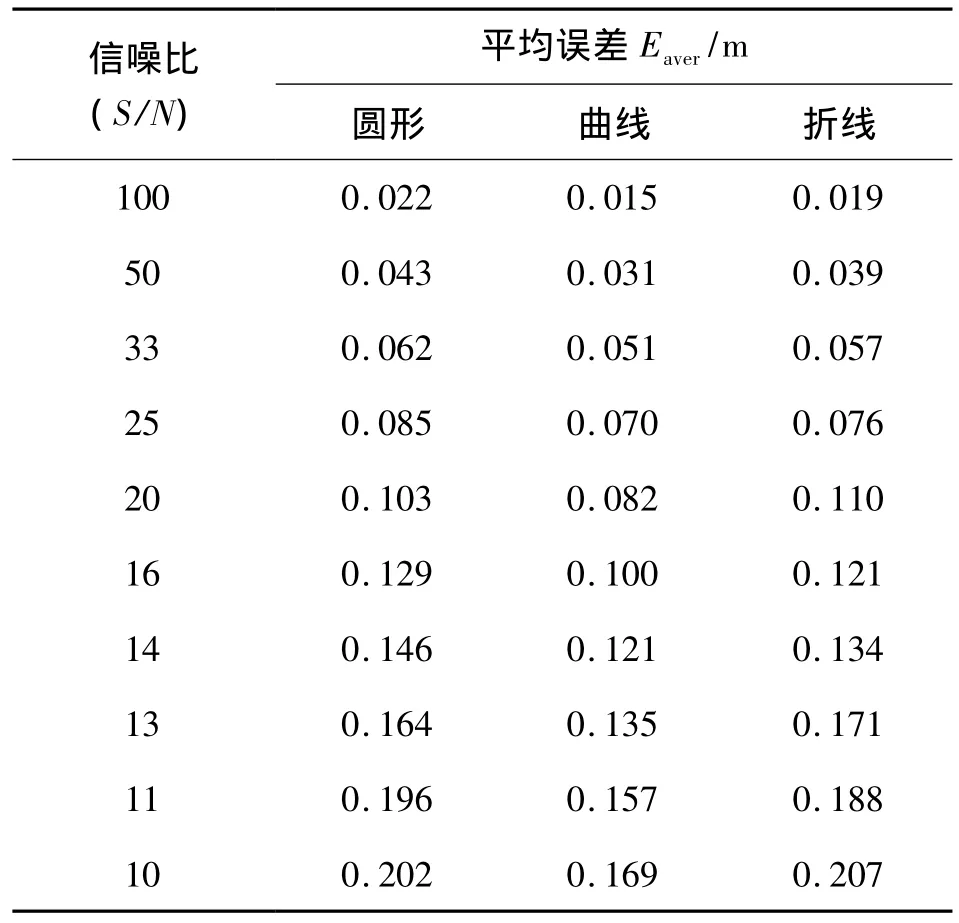
表1 不同信噪比下的多种形状位置跟踪平均误差Eaver

3.2 系统与实验

整个电磁定位系统包括发射线圈、信号控制处理电路、接收线圈。正弦波信号经功率放大后驱动发射线圈产生交变磁场。传感线圈上接收到的电压信号经过放大与滤波处理。最后微控制器STM32F103自带ADC采集电压信号并处理，进一步计算得到目标的位置参数。系统电路框图如图4所示。

图4 系统电路框图

发射线圈与接收线圈设计:考虑到大范围的跟踪，信号发射线圈必须有大的激励电流和较大的尺寸。发射线圈的尺寸较大，若采用3个互相正交的线圈作为发射源，则整个发射源的体积会相当大，比较占空间，此时可以将发射源做成单个线圈或互成一定角度的双轴线圈。本实验采用单个发射线圈作为信号发射器。而接收线圈的尺寸相对小很多，可以做成3个互相正交的线圈接收器。发射线圈和接收线圈设计与布局如图5所示。

选用芯片MAX038来产生正弦波信号，将发射信号频率设置为2 kHz左右。发射线圈选用直径为0.35 mm的漆包线。线圈的半径缠为32 cm，绕制约300匝。测得绕制发射线圈的电阻大小为107.4 Ω。由于磁场信号随着距离的增加衰减快(与距离的三次方成反比)，要在较远的地方感应到磁场信号的变化，需要对发射线圈施加较大的激励信号。因此选用NS公司的大功率音频放大集成电路芯片LM3886TF放大信号。传感线圈选用直径为0.08 mm的漆包线。将三轴接收线圈的半径缠为0.5 cm，分别绕制约1 600匝左右。实际测得三轴线圈上的电阻分别为96.2 Ω、96.7 Ω和99.8 Ω。为增大磁导率，线圈内放有磁芯。变化的磁场信号在三轴接收线圈上分别产生3个电压信号。这时的电压信号非常微弱，需要经过放大处理。此处选用放大器AD620。

图5 发射线圈和接收线圈设计与布局

接收线圈上的3路电压信号最终通过微控制器STM32F103的ADC进行采集。微控制器STM32F103的ADC是12位的逐次逼近型模拟数字转换器。它有18个通道，可测量16个外部和2个内部信号源。将3路电压与其3个ADC通道相连，按顺序对3个通道的电压信号依次进行转换。为避免寄存器中的数据丢失，使用STM32微控制器的DMA(直接存储器存取)功能。通过配置，单个通道的电压采样周期为7 μs，则3个通道的总采样周期为21 μs。因为正弦波发射信号频率为2 kHz，所以一个正弦波周期内每个通道可以采样约23个样本点。电压幅值可以通过系统软件进行拟合计算得出。空间位置则可以由得到的电压幅值进一步推理得到。

在电磁定位的系统实验中，整体组成与布置如图6所示。我们将发射线圈固定方法与上述仿真方法一致，使接收传感器在平面z=－0.12上做定点运动。事先通过标定反推计算得出BT1=12.740 6，BT2=9.433 3，BT3=7.251 9。系统在测得3个正交接收线圈上的电压后，可计算得到接收线圈所在位置，且界面显示功能可以在液晶屏上显示实时位置，如图6(c)所示。在平面上选取多点进行定位实验，得到的实验数据如表2及相应图7所示。

图6 电磁定位系统

表2 系统所测数据

图7 真实位置与系统所测位置对比

4 结果分析

在表2与图7中，可以看到多数系统测得点与接收线圈实际所处位置的平均误差为7.16 cm。这处于仿真情况下的信噪比为25与33之间的情况，表明实际实验中受到一定程度的噪声影响，且这是不可避免的。有部分点与实际位置偏差较大，最大的甚至达到9.44 cm，这不仅是受到噪声的影响，还与人为的操作有着一定的关系。前面提到过接收线圈的旋转角度α、β和γ都为0°，而实验中接收线圈的位置不可能被摆成精确的无旋转角度，总会有些角度偏差，这就产生了人为的误差。设置硬件一端口在定位程序开始时为高电平，程序结束时为低电平。在整个程序的循环运行中，可以从示波器上读到系统定位的响应时间约0.3 s。总体上看，系统定位的准确度和时效在可以接受的范围内。

5 讨论

本文所研究的内容为电磁定位在平面上的简化应用。此应用为一套基于嵌入式系统ARM (STM32)实现的定位跟踪系统。其利用解析法求解位置，可以解决实际生活中平面上的定位需求。本系统平面上的定位精确度在10 cm内，但还需要在一定程度上提高。移动目标在实际中也存在着角度旋转的情况，而本文没有考虑角度问题，怎样将角度求解引入平面定位中是下一步急需解决的问题。生活中也存在着不少空间定位的需求。因此，寻求一种高效的空间定位算法，将电磁定位系统在大范围平面上的应用拓展至较大空间上，也是需要进一步研究的地方。

［1］Hu Chao，Meng M Q H，Mandal M.Efficient Magnetic Localization and Orientation Technique for Capsule Endoscopy［J］.International Journal of Information Acquisition，2005，2(1):23－36.

［2］Hu Chao，Meng M Q H，Mandal M.A Linear Algorithm for Tracing Magnet Position and Orientation by Using Three-Axis Magnetic Sensors［C］//IEEE Transactions on Magnetics，2007，43(12): 4096－4101.

［3］Yang W，Hu Chao，Meng M Q H，et al.A New 6D Magnetic Localization Technique for Wireless Capsule Endoscope Based on a Rectangle Magnet［J］.Chinese Journal of Electronics，2010，19(2): 360－364.

［4］李金，郑小林，侯文生，等.一种用于消化道内微型装置磁定位的非线性方法［J］.仪器仪表学报，2009，30(3):895－897.

［5］徐彤，王涌天.虚拟现实系统中六自由度电磁跟踪算法的改进［J］.传感技术学报，2000(3):204－210.

［6］Anderson P T.Electromagnetic Tracking System and Method Using a Single-Coil Transmitter［P］.US Patent，7158754B2，2007.

［7］Schneider M.Measuring Position and Orientation Using Magnetic Fields［P］.US Patent，6073043，2000.

［8］Wang X，Song Shuang，Hu Chao.The Extraction Technology of Weak Coupling AC Signal in an Electromagnetic Localization System［C］//Proceedings of the 2010 IEEE International Conference on Robotics and Biomimetics，2010:1170－1175.

［9］Li M，Song Shuang，Hu Chao，et al.A Novel Method of 6-DoF E-lectromagnetic Navigation System for Surgical Robot［C］//Proceeding of the 8th World Congress on Intelligent Control and Automation，2010:2163－2167.

［10］Wilamowski B M.Improved Computation for Levenberg-Marquardt Training［C］//IEEE Transactions on Neural Netwoks，2010，21 (6):930－937.

［11］师晓宙，胡超，向望华，等.用于骨科手术机器人的电磁定位方法［J］.传感技术学报，2011，24(11):1569－1573.

［12］吴旭东，侯文生，郑小林，等.磁偶极子的定位模型及实验验证［J］.仪器仪表学报，2008，29(2):895－897.

［13］Hu Chao，Song Shuang，Wang X，et al.A Novel Positioning and O-rientation System Based on 3-Axis Magnetic Coils［C］//IEEE Transactions on Magnetics，2012，48(7):2211－2219.

［14］Yang W，Hu Chao，Li Mao，et al.A New Tracking System for Three Magnetic Objectives［C］//IEEE Transactions on Magnetics，2010，46(12):4023－4029.

［15］Mukundan R.Quaternions:From Classical Mechanics to Computer Graphics，and Beyond［C］//Proceedings of the 7th Asian Technology Conference in Mathematics，2002，97－106.

［16］Shuster M D.A Survey of Attitude Representations［J］.The Journal of The Astronautical Sciences，1993，41(4):439－517.

包建孟(1987－)，男，浙江乐清人，宁波大学计算机应用技术专业硕士研究生，研究方向为信息集成技术与智能控制;

胡超(1960－)，男，浙江宁海人，浙大宁波理工学院三江学者特聘教授，博士生导师，从事传感器技术研究。

平面电磁定位跟踪系统*

包建孟1，2，胡超2*，林卫星1，王文虎1，2，王涛1
(1.宁波大学，宁波315211;2.浙江大学宁波理工学院，浙江宁波315100)

通电线圈常被用作电磁定位装置收发器，应用在移动目标或机器人的实时位置跟踪任务中。系统的激励线圈磁场分布模型、信号发生提取电路和定位算法软件都影响系统定位的精度。本文采用磁偶极子模型，针对平面移动目标跟踪定位的特殊情况，设计基于嵌入式系统ARM(STM32)的大范围平面运动的定位系统。系统采用单发射线圈三接收线圈方案，及一种解析法求解目标位置的算法，可以定位离信号源数米范围内的移动目标。从仿真与实验中验证其可以很好的求解平面一类移动目标位置，平均误差在10 cm内。系统的定位精度满足大部分定位需要。

电磁定位;平面跟踪;磁偶极子;线性求解;嵌入式系统

TP212.9

A

1004－1699(2014)04－0518－06

2014－01－09修改日期:2014－04－02

C:3120J

10.3969/j.issn.1004－1699.2014.04.018

项目来源:国家自然科学基金项目(61273332);宁波市自然科学基金项目(2012A610005)