Investigation of the Acoustic Performance of Piezoelectric Composites Based on Yamada Model*

YANG Dan，WANG Tao，XIAO Han，ZHAO Sanxing

(College of Mechanical Automation，Wuhan University of Science and Technology，Wuhan 430081，China)

Investigation of the Acoustic Performance of Piezoelectric Composites Based on Yamada Model*

YANG Dan*，WANG Tao，XIAO Han，ZHAO Sanxing

(College of Mechanical Automation，Wuhan University of Science and Technology，Wuhan 430081，China)

A method of analyzing acoustic performance of piezoelectric composites based on Yamada model is proposed.First，a passive acoustic model of 0－3 piezoelectric ceramic/rubber composites is established.Then，the equivalent parameters of 0－3 piezoelectric ceramic/rubber composites is obtained by Yamada model and embedded into the acoustic model.Finally，theoretical calculation and comparative analysis of the absorption coefficient of the piezoelectric composites with different parameters is carried out.Conclusions show that when piezoelectric composites passively absorb，the polymer plays a major role on the attenuation of acoustic energy.

piezoelectric composites;Yamada model;acoustic absorption;acoustic energy

压电复合材料是由压电陶瓷相和聚合物相按照一定的连通方式、体积比例和空间几何分布复合而成的一类重要的力电耦合功能材料，这种复合方式可以大幅地提高压电材料的某些压电性能［1－2］。压电复合材料兼具压电陶瓷和聚合物的长处，具有很好的柔韧性和加工性能，特别是由于其具有较低的密度，因而与普通压电陶瓷相比更容易与空气、水、生物组织实现声阻抗匹配，现已广泛的应用于水听器、阻尼器、作动器、换能器和传感器［3－8］等方面。压电复合材料的性能不仅与材料的组成成分及各组分所占的比例有关，而且还与两相的连通形式密切相关。按照两相材料不同的连通方式，压电复合材料共可分为10种类型，其中第1个数字代表压电陶瓷的连通维数，第2个数字代表聚合物的连通维数，而0－3型压电复合材料就是由压电陶瓷颗粒均匀分散(在三向都不连通即为0维)在三维连通的聚合物基体中形成的［9］。

近年来，对于压电复合材料的研究主要集中在有限元法确定其电荷分布，串并联外接电路以进行减振吸声和采用实验法确定其损耗因子等方面，而对其自身吸声机理的研究则非常少［10－12］。Yamada模型是Yamada于1985利用Maxwell-Garner方程推出的0－3型压电复合材料的压电常数估算式，相比Furukawa模型、Cubes模型和Dilute等模型而言，它具有估算结果精确、计算方便快捷等优点，这一估算式现已获得广泛的认可［13－14］。本文首先建立了0－3型压电陶瓷/橡胶复合材料的被动吸声模型，然后运用Yamada微观模型获得0－3型压电陶瓷/橡胶复合材料的等效参数，并将此等效参数嵌入到吸声模型，对压电复合材料的吸声性能进行了数值仿真分析。

1 声学覆盖层模型

声学覆盖层的结构如图1所示，模型为圆片形压电复合材料层，其厚度为d，半径为a，并且d≥a。x3为压电复合材料的厚度方向，也是其极化方向，假设压电复合材料在径向是同性的，当声波垂直入射到压电复合材料时，只有x3方向的扰动，因此也只与压电复合材料在这个方向上的相关常数有关。

图1 声学覆盖层结构图

根据以上的假设，压电复合材料前后表面受力和质点速度与电压、电流之间的关系式为［15］:

压电复合材料前后接触均匀紧密，因此其质点受力及速度满足以下连续条件:

其中R1和R2分别为前后媒质的特性阻抗，Pi，Pr，Pt分别为入射声压、反射声压及投射声压。

将连续条件式(2)代入式(1)可得［16］:

33d/ω)，θ=kd。

考虑压电复合材料被动吸声，J=0，因此，当压电复合材料前后媒质确定并且已知入射声压时，可由式(3)求得其他未知量，进而求得压电复合材料的表面吸声系数:

2 Yamada模型

Yamada模型假设压电陶瓷颗粒为分散相，聚合物为连续相，压电陶瓷均匀分布在聚合物中。在大量实验的基础上，得到了压电复合材料的宏观压电性能与其组分几何、物理性质及组成比例之间的关系:

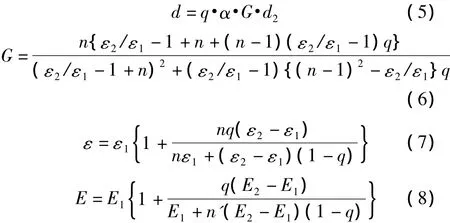
其中d，ε和E分别为压电复合材料的压电常数、介电常数和弹性常数，ε1和E1分别为聚合物的介电常数和弹性常数，d2，ε2和E2分别压电陶瓷颗粒的压电常数、介电常数和弹性常数。α为极化率，q为压电陶瓷与压电复合材料的体积比。

n'为:

其中σ为聚合物的泊松比。

将由式(5)～式(8)得到的不同体积比、厚度和形状参数的压电复合材料的等效参数代入到原吸声模型，就可得到压电复合材料的吸声系数。

3 数值仿真及分析

通过对相关资料的查阅，确定数值计算所采用压电复合材料的参数分别为:E1=0.79×109N/m2，ε1=0.76×10－9F/m，ρ1=956 kg/m3，E2=6.32×109N/m2，ε2=16.4×10－9F/m，d2=184×10－12C/ N，ρ2=4 786 kg/m3，α=0.85，n'=0.67。

理论计算所得的不同体积比、厚度和形状参数的压电复合材料的吸声系数如图2～图4所示。

图2 不同体积比下压电复合材料的吸声系数

图3 不同厚度压电复合材料的吸声系数

图4 不同形状参数压电复合材料的吸声系数

通过对图2～图4的分析可以看出:(1)压电复合材料的被动吸声系数随着频率的增加都呈增加的趋势，但随着压电陶瓷颗粒体积比的增加而产生一定的下降，这说明在压电复合材料被动吸声时，对声能量的衰减起主要作用的为聚合物相。这是由于压电复合材料此时处于断路状态，使得压电陶瓷相中因压电效应由声能转化而成的电能并不能在电路中进行有效耗散，所以对声能的吸收非常有限。因此要想使得压电复合材料在低频段具有较好的吸声性能，就必须加入控制电路，引入主动控制模型。(2)随着压电复合材料厚度的增加，其吸声系数有一定的上升，特别是中频带的吸声系数增加较快。也就是当厚度增加时，其吸声频带有向中频带移动的趋势，与聚合物吸声性能的特性比较相似。(3)随着陶瓷相形状参数的改变，压电复合材料的吸声系数也有一定的改变。形状参数与陶瓷相颗粒的尺寸关系比较复杂，总体上形状参数与颗粒尺寸同向变化。随着形状参数的减少，中低频带的吸声系数有一定的下降，但是高频带有了一定的增加。

4 结论

本文运用压电复合材料的Yamada微观模型获得0－3型压电陶瓷/橡胶复合材料的等效参数，并将此等效参数嵌入到建立的吸声模型中，对不同体积比、厚度和形状参数的压电复合材料进行了数值仿真分析，计算结果表明:压电复合材料被动吸声时，聚合物对声能量起主要衰减作用;随着压电复合材料厚度的增加，吸声系数(特别是中频带)有较大增加;随着压电复合材料形状参数的减少，中低频带的吸声系数有一定的下降，但是高频带有一定的增加。下一步，将对加入被动振荡电路或者主动压电控制的压电复合材料的吸声性能进行研究，进而来改善低频段的吸声效果。

［1］Klicker K A，Bigger J V，New R E.Composites of PZT and Epoxy for Hydrostatic Transducer Applications［J］.J Am Ceram Soc，1981，64(1):5－9.

［2］Guruaja T R，Schulze W A，Shrout T R，et al.High Frequency Applications of PZT/Polymer Composite Matericals［J］.Ferroelectrics，1981，39:1245－1248.

［3］Lum Paul，Greenstein Michael，Grossman Charles，et al.High Frequency Membrane Hydrophone［J］.IEEE Transactions on Ultrasonics，and Frequency Control，1996，43(4):536－544.

［4］张志甜，张超，冯冠平.基于横向场激励的高频压电超声换能器［J］.传感技术学报，2010，23(4):461－464.

［5］高恒垣，王莹，李书.压电复合材料机翼振动控制研究［J］.振动、测试与诊断，2013，33(1):107－110.

［6］王涛，罗毅，刘绍鹏.基于压电主动传感方式的螺栓松动检测实验研究［J］.传感技术学报，2013，26(8):1059－1063.

［7］Thorp O，Ruzzene M，Baz A.Attenuation and Localization of Wave Propagation in Rods with Periodic Shunted Piezoelectric Patches［J］.Smart Mater Struct，2001，10:979－989.

［8］Bin Lin.PVDF and PZT Piezoelectric Wafer Active Sensors for Structural Health Monitoring［J］.ASME，2005，IMECE2005－80400:69－76.

［9］游达，董玉林，张联盟.陶瓷/聚合物压电复合材料的国内外概况和应用展望［J］.新材料产业，2002，106(9):25－29.

［10］代螺，黄志雄，石敏先.基于ANSYS的0－3型压电复合材料电荷分布［J］.复合材料学报，2013(3):220－224.

［11］安占营，陈雨，黄润.耗散因子的压电等效电路参数确定法［J］.传感技术学报，2009，22(7):965－972.

［12］于利刚，李朝晖，马黎黎.0－3型压电复合材料覆盖层水下吸声性能的理论研究［J］.物理学报，2012，61(2):74－78.

［13］罗大兵，张玉.0－3型压电复合材料Yamada模型改善［J］.江汉大学学报(自然科学版)，2008，36(3):48－50.

［14］Yamada T，Ueda T，Kitayama T.Piezoelectricity of a High Content Lead Zirconate Titanante/Polymer Composite［J］.Journal of Applied Physics，1982，53(4):4328－4332.

［15］Berlincourt D A，Currant D R，Jaffe H.Piezoelectric Piezomagnetic Materials and Their Function Intransducers［J］.Physical Acoustics:Principles and Methods，Edited by W P Mason，New York， 1964:169－270.

［16］Shields F D，Hendrix J E，Lafleur L D.Smart Acoustically Active Surfaces［J］.J Acoust Soc Am Suppl，1989，185:S62.

杨丹(1982)，男，博士，讲师。主要研究方向为智能材料与结构的主动减振降噪、故障诊断，yang－dan2000@ 163.com。

基于Yamada模型的压电复合材料吸声性能的研究*

杨丹*，王涛，肖涵，赵三星
(武汉科技大学机械自动化学院，武汉430081)

提出了一种运用Yamada微观模型来分析压电复合材料吸声性能的方法.首先，建立了0－3型压电陶瓷/橡胶复合材料的被动吸声模型;然后，运用Yamada微观模型获得0－3型压电陶瓷/橡胶复合材料的等效参数，并将此等效参数嵌入到吸声模型;最后，对不同参数下的压电复合材料的吸声系数进行了理论计算和对比分析.结论表明:压电复合材料被动吸声时，聚合物对声能量的衰减起主要作用。

压电复合材料;Yamada模型;吸声;声能量

TN911.4

A

1004－1699(2014)04－0452－04

2014－01－16修改日期:2014－04－01

C:0585

10.3969/j.issn.1004－1699.2014.04.006

项目来源:武汉科技大学校基金项目(2012XZ005);国家自然科学基金面上项目(51375354);国家自然科学基金青年基金项目(51105284)