动荷载作用下预测玻璃板破坏强度和破坏时间的一种改进模型——Ⅱ.参数确定及验证

柳锦春，于润清，唐德利

(1.解放军理工大学 国防工程学院，南京 210007;2.爆炸冲击防灾减灾国家重点实验室，南京 210007)

裂纹的开裂直接导致玻璃的破碎，文献[1]采用蒙特卡洛法并结合有限元分析，建立一种修正的单层玻璃板动态裂纹破坏模型。本文结合试验确定该修正模型中的未知量，即裂纹分布密度、最大裂纹长度和裂纹长度的分布，最后用此模型计算了爆炸荷载下玻璃板的破坏时间。

1 确定改进模型中的未知量

1.1 网格和材料参数的确定

选用ABAQUS进行玻璃板的动力分析，在模拟前有必要确定网格尺寸和材料参数。取弹性模量E=73 GPa，泊松比v=0.25，密度ρ=2 450 kg/m3，板的尺寸为1 m×1 m×0.004 m，边界条件为四边简支，荷载为均布荷载2.2 kPa，为准确模拟准静态加载[2]，荷载步选用光滑缓慢加载步，加载时间设为2 s，经过网格尺寸分析取网格为50 mm，分别用几何线性和几何非线性进行计算，并将计算结果与其他文献[3,4]的计算结果作对比，见表1。

表1 应力和挠度的对比

由表1可以看出，运用ABAQUS软件及上述参数可以很好地模拟玻璃的变形(本文如无特殊说明玻璃板的材料参数均为1.1节确定的参数)。此外，从表中还可以看出，运用几何非线性计算的结果要小于用几何线性计算的结果，由于玻璃薄板在动荷载作用下几何非线性特征明显[5]，因此本文选用几何非线性进行计算。

1.2 时间增量步Δt的确定

裂纹长度随时间变化而增大，可表示为[1]

(1)

式中:aj、aj-1分别是第j时刻、j-1时刻的裂纹长度，σj、σj-1分别是j时刻、j-1时刻的裂纹法向拉应力，Δt为时间增量，v0和n均为材料参数，KIC是应力强度因子，Y是裂纹的形状参数。

由式(1)可知，Δt的值直接影响计算结果。取Δt分别为0.02 s，0.05 s，0.1 s，板的尺寸、材料参数、荷载形式和边界条件与1.1节相同，玻璃板内的裂纹分布取对数正态分布(参数见表2)，裂纹密度与裂纹最大长度见表3，样本取100，计算破坏时间t的累计概率(CPD)，如图1所示。观察图1，比较三组数据，综合考虑计算精度和计算效率，可取Δt=0.05 s。

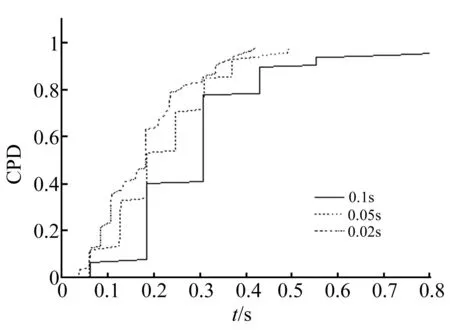
图1 不同增量步破坏时间的对比

1.3 裂纹长度分布函数的参数取值

设定最大裂纹长度amax，将任意裂纹长度aj除以最大裂纹长度，得长度归一化系数rj。对rj取不同的分布即可代表裂纹不同的长度分布。Nurhuda采用的概率密度函数[6]使rj在某一区间过于集中，如图2所示，在取对数正态分布时长度在较小值区间过于集中。为更好的覆盖整个取值范围，本文采用图3所示的概率密度函数，详细参数见表2。

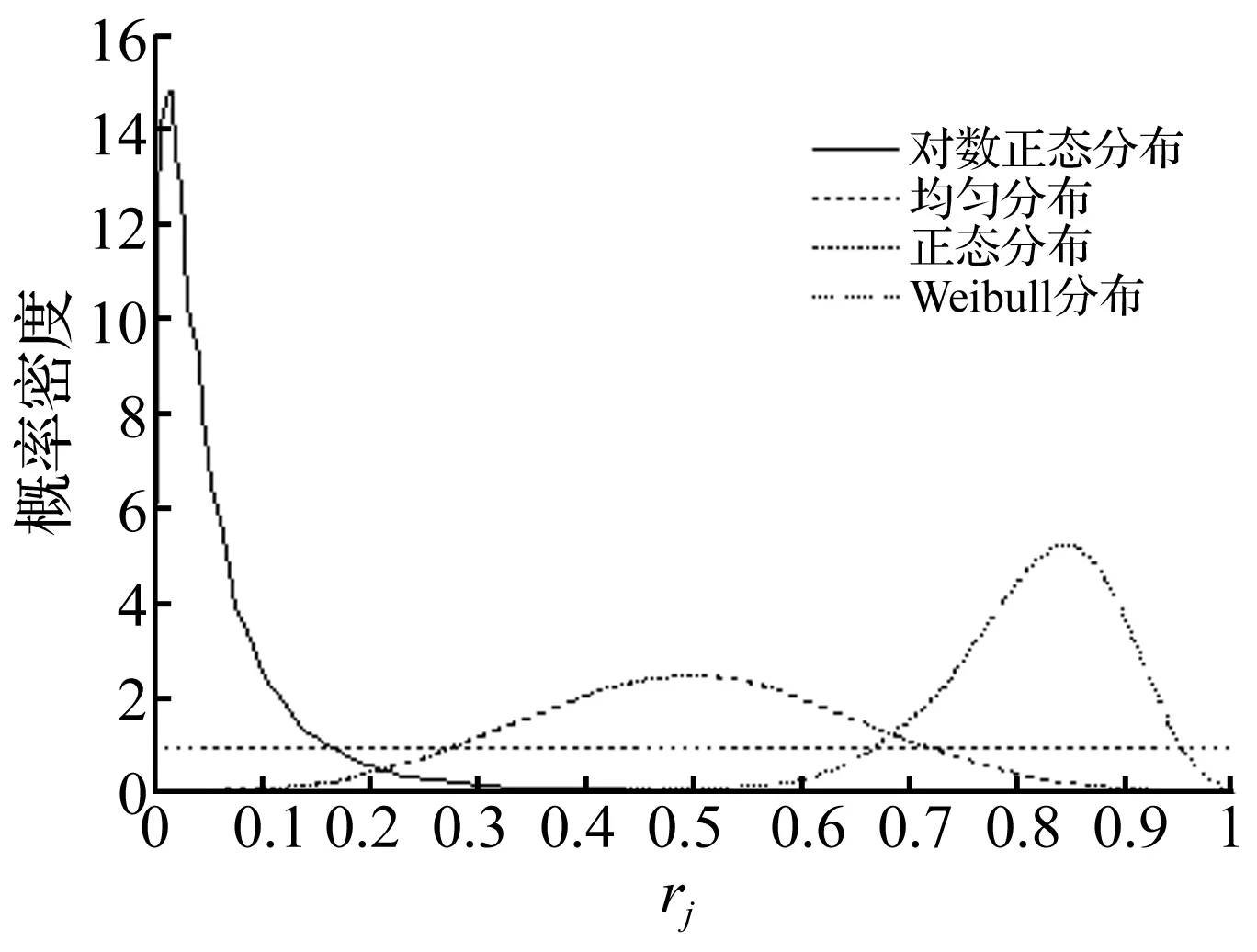
图2 Nurhuda 采用的概率密度函数

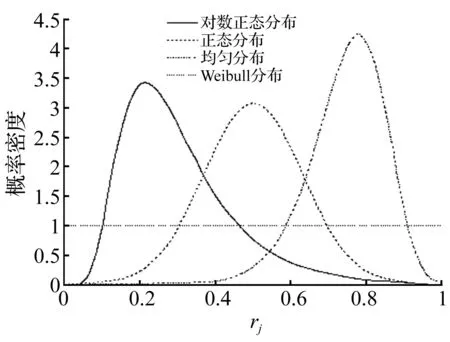
图3 本文采用的概率密度函数

表2 不同分布参数取值

1.4 确定裂纹长度分布、裂纹密度和裂纹最大长度

Gavanski等[4]研究了浮法玻璃板的破坏时间，通过试验统计了破坏时间的累计概率，Nurhuda等[6]对浮法玻璃板的破坏应力做了试验研究，统计了破坏应力的累计率，本节参照这两个试验进行参数确定和模型的验证。具体做法如下：

(1) 确定每种裂纹长度分布对应的裂纹密度和最大裂纹长度。Gavanski等[4]统计了三种加载形式(如图4所示)下玻璃板破坏时间的累计概率，选用其中一个加载速率的试验结果，用四种不同的裂纹长度分布进行模拟，得到四种裂纹长度分布对应的裂纹密度和最大裂纹长度。

(2) 对比破坏应力。仍用(1)中具体确定四组参数，对Nurhuda的一组试验中的其中一个进行模拟，对比模拟结果与试验值，判断参数的优劣。

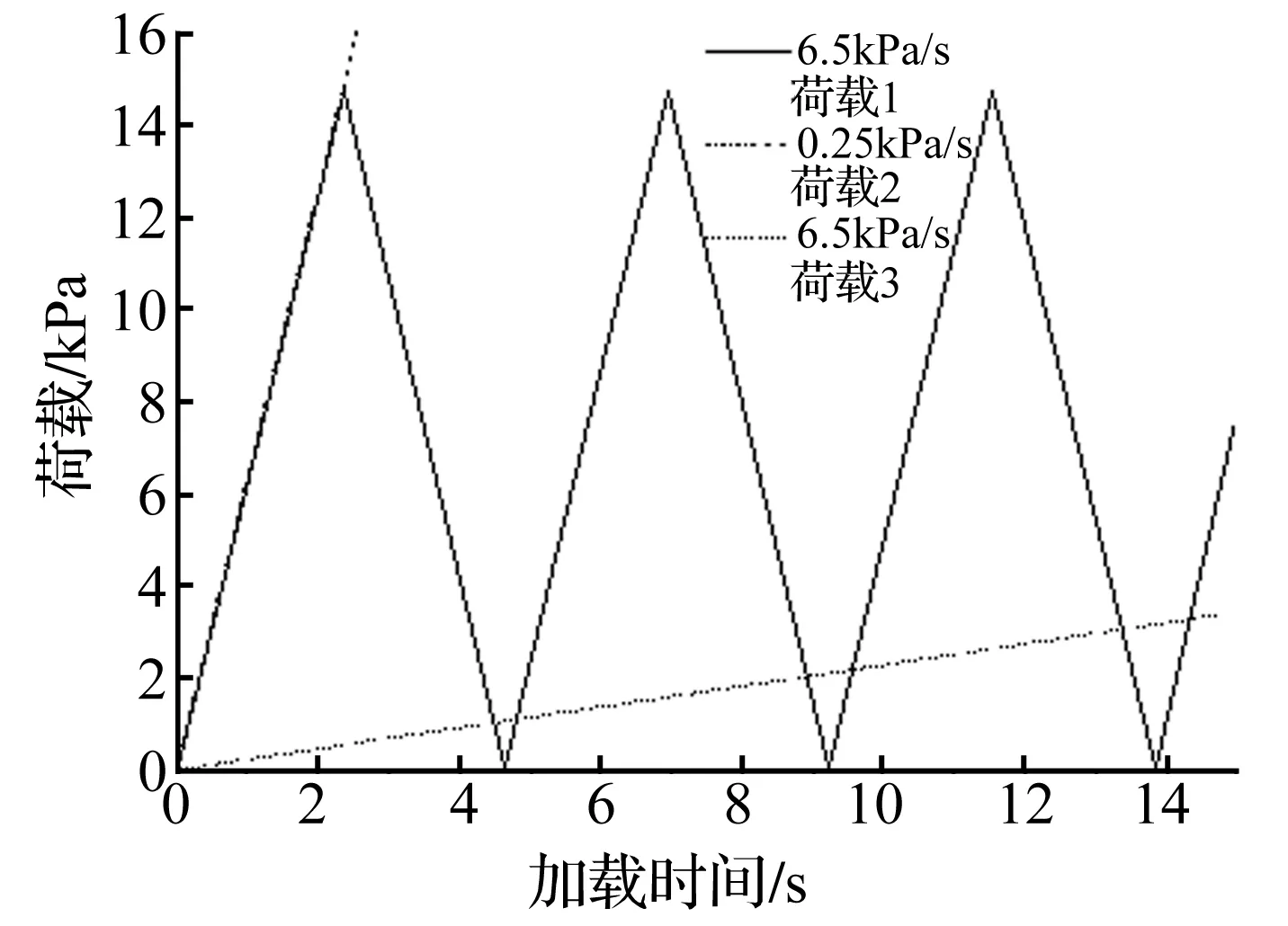
图4 不同的荷载形式

1.4.1 确定四种裂纹长度分布对应的裂纹密度和最大裂纹长度

取加载速率为6.5 kPa/s(图4中的荷载3)，玻璃板尺寸为1 m×1 m×0.006 m，对四种长度分布函数，确定出对应的最佳裂纹密度和裂纹最大长度。

由于Gavanski等[4]对不同的荷载形式只取了20个试件，因此在模拟计算时每组的试件数取为20，共模拟15组。选取不同的裂纹密度值和最大长度值，取模拟结果的平均值与实验结果最近似的参数为最佳参数。

以对数正态分布为例，对每组玻璃板进行模拟，统计出累计概率，如图5。然后计算出15组玻璃板的模拟结果，如图6所示。最后求出15组模拟结果的平均值，见图7。

由式(2)计算平均值与实验值的距离[8]，取距离最小的参数为最优参数。

(2)

其中:t1k为破坏时间的试验值，t2k为破坏时间的模拟值。

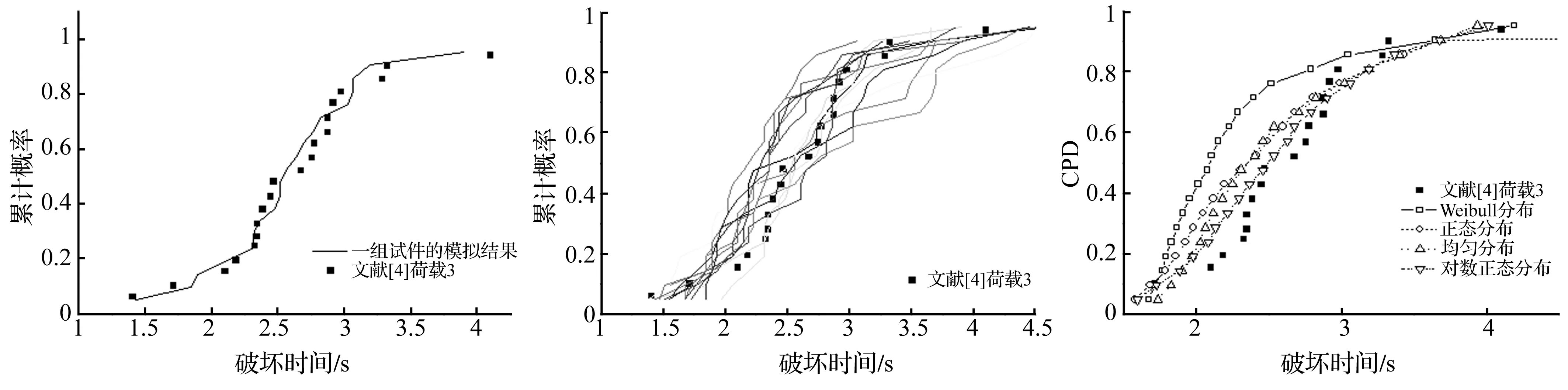
图5 对数正态分布1组模拟结果(荷载3)

用同样的方法确定出其他长度分布所对应的最佳裂纹分布密度和最大长度，计算结果见表3。

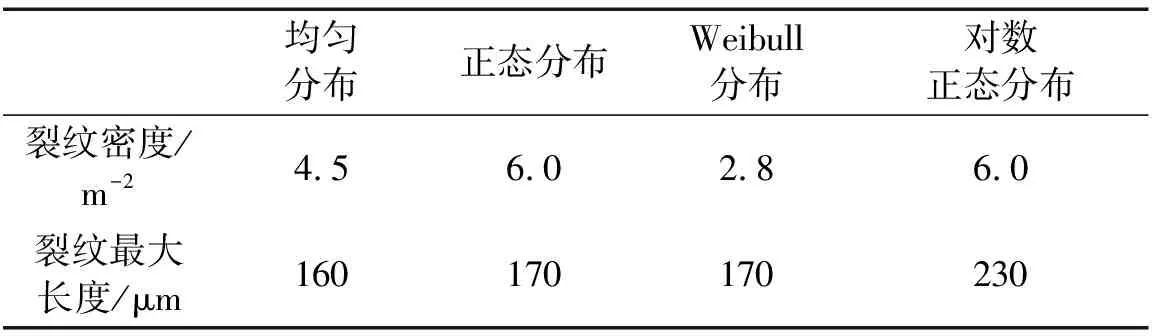
表3 裂纹尺寸分布的统计参数

1.4.2 对比破坏应力，确定参数

取Nurhuda的一组试验[6]中的一个工况计算玻璃板破坏应力的累计概率。加载速率取为10 kPa/s，玻璃尺寸分别为2 m×0.67 m×0.008 m，玻璃板为四边简支，计算结果如图8。

图8 模拟结果与试验结果的对比

图8表明，采用对数正态分布计算的破坏应力与试验结果更加接近。

由此确定玻璃板内裂纹长度大致符合对数正态分布。

2 与其他模型的对比

在确定参数后，将该改进模型与其他模型相比较，并与试验值进行对比，以确定模型的优劣性。由于同时给出破坏时间和破坏应力的实验数据较少，因此在计算破坏时间时与Evans的模型[4]和Simu&Reed的模型[4]进行对比，在计算破坏应力时与Nurhuda模型[6]和Beason的玻璃破坏模型[7]进行对比。

取Gavanski等[4]的试验，针对荷载1、荷载2(图4)计算玻璃板的破坏时间，并与Evans的模型和Simu&Reed的模型进行对比，如图9、图10。由图9可知，在6.5 kPa/s的锯齿形荷载下，改进模型结果与试验值吻合较好，Simu&Reed模型结果偏差小一点，但当累计概率(CPD)越来越大时偏差也越来越大，而Evans模型结果始终与试验值偏差均较大。由图10可知，在0.25 kPa/s的直线型荷载下，当累计概率(CPD)小于0.7时，改进模型与Simu&Reed的模型结果与试验值吻合均较好，而Evans的模型与试验值偏差较大，当累计概率(CPD)大于0.7时，只有改进模型与试验值吻合较好，而其他两种模型与试验值吻合都较差，尤其是Evans模型偏差较大。

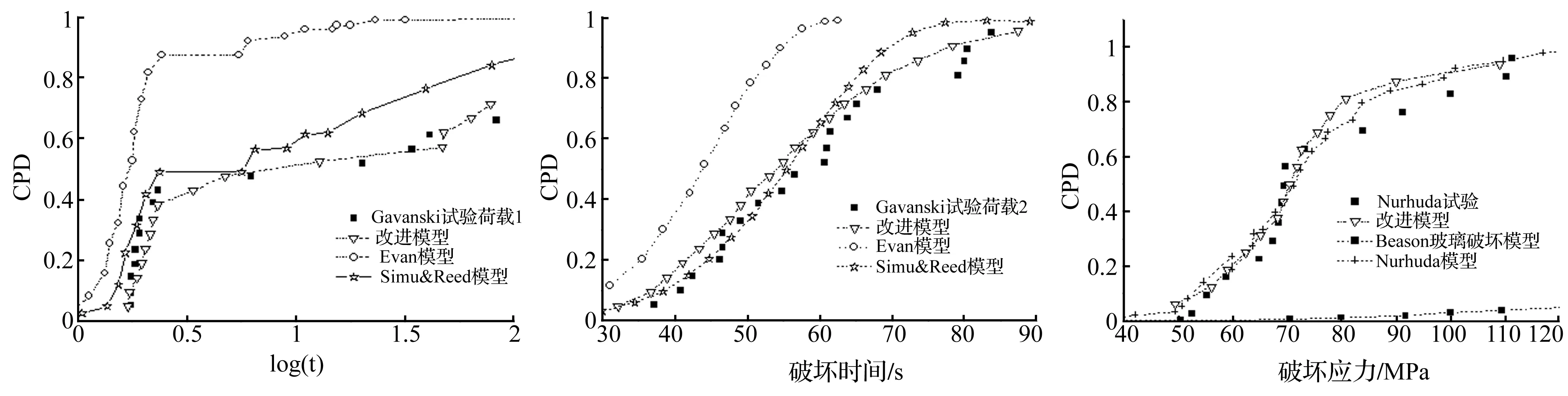
图9 模型对比(荷载1)

取Nurhuda的试验[6]计算玻璃板破坏应力的累计概率。加载速率取为10 kPa/s，玻璃尺寸为2 m×0.4 m×0.008 m，玻璃板为四边简支，运用改进模型和Nurhuda模型[6]以及Beason模型计算破坏应力并与试验值进行对比，如图11。由图11可以看出，Beason模型预测的破坏应力过大，而改进模型与Nurhuda模型值与试验值误差较小。但相对于Nurhuda模型，改进模型不仅可以分析预测玻璃板的破坏应力，还可以分析预测玻璃板的破坏时间，且不受玻璃板形状和边界条件的限制。

3 爆炸荷载条件下破坏模型的适用性验证

葛杰[9]对不同爆炸荷载作用下玻璃板的动力响应进行了试验研究，如表4，本节根据前文确定的裂纹密度、裂纹长度分布和最大裂纹长度，对表4中的三种工况进行模拟。

爆炸荷载的时程曲线可由修正的Friedlander方程确定，

(3)

其中:pmax是冲击波超压峰值，td是正压作用时间，b是波形参数，均可由Conwep[10]计算得出。

表4 不同工况 [9]

图12 模拟的破坏时间分布

玻璃材料参数根据文献[9]取值，玻璃的弹性模量E=67 GPa，泊松比v=0.25，选取5组样本，每组900个，根据改进模型，采用前文确定的最优的裂纹长度分布和相应的裂纹密度、最大裂纹长度，计算爆炸荷载作

用下玻璃板的破坏时间，结果如图12所示。对比三种工况可知，随着比例爆距的减少，破坏时间的主要分布区间前移，工况1和工况2玻璃板的破坏时间集中在2～4 ms，工况3集中在0～2 ms，这与实验结果是基本相符的，说明该破坏模型可以用于单层玻璃板的抗爆分析。

4 结 论

本文以浮法玻璃为例确定了文献[1]中修正模型的未知量。首先假定四种不同的裂纹长度分布，分别对其中某一种长度分布选用不同裂纹密度值和裂纹最大长度值，基于所选的裂纹密度和裂纹最大长度对玻璃的破坏时间进行模拟，通过计算模拟结果与试验结果的对比确定出四种裂纹长度分布对应的最优裂纹密度和裂纹最大长度。根据确定的四种长度分布及最优裂纹密度和裂纹最大长度，计算玻璃板的破坏应力，将计算结果与试验结果对比，确定出最优的裂纹长度分布，由此，最优裂纹长度分布对应的一组参数即为该改进模型的参数。运用确定参数后的改进模型计算了玻璃板的破坏时间和破坏应力，分别与Evans的模型、Simu&Reed的模型、Nurhuda模型和Beason模型的计算结果进行对比，对比表明，该改进模型可以同时较准确地计算出玻璃板的破坏应力和破坏时间。最后应用改进模型，采用最优的裂纹长度分布和相应的裂纹密度和最大裂纹长度对不同爆炸荷载下玻璃板的破坏时间进行了模拟，模拟结果与试验值吻合较好。

[1] 柳锦春, 于润清, 唐德利. 动荷载作用下预测玻璃板破坏强度和破坏时间的一种改进模型——Ⅰ.理论[J]. 振动与冲击, 2014,33(13):77-81.

LIU Jin-chun, YU Run-qing, TANG De-li. Improved prediction model for failure strength and failure time of glass panels under dynamic loading-Ⅰ. Theory [J]. Journal of Vibration and Shock, 2014,33(13):77-81.

[2] Analysis user’s manual of ABAQUS 6.6 Volume III：Prescribed Conditions[P]. American: ABAQUS Inc., 2007.

[3] Fischer-Cripps A C, Collins R E. Architectural glazing: Design standards and failure models [J]. Build. Environ, 1995, 30(1): 29-40.

[4] Gavanski E, Gregory A K, ASCE M. Glass breakage tests under fluctuating wind loads [J]. American Society of Civil Engineers, 2011, 3: 34-41.

[5] Mehmet Z A. Laminated glass plates: revealing of nonlinear behavior [J]. Computers and Structures, 2003, 81: 2659-2671.

[6] Nurhuda I, Lam N T K, Gad E F, et al. Estimation of strength in large annealed glass panels [J]. Int. J. Solids Struct., 2010,47(18 19): 2591-2599.

[7] Beason. W L, Morgan. Glass failure prediction model [J]. J. Struct. Eng., 1984, 110(2): 197-212.

[8] 姚泽清, 苏晓冰, 郑琴, 等. 应用泛函分析[M]. 北京：科学出版社, 2007.

[9] 葛杰. 爆炸荷载作用下建筑玻璃板的破碎理论与实验研究[D]. 上海：同济大学, 2012.

[10] Hyde D. Conventional weapons program (Conwep)[R]. US Army Waterways Experimental Station, Vicksburg. USA, 1991.