考虑基底层阻尼的自由阻尼结构损耗因子修正公式

吴晴晴，王敏庆

(西北工业大学 航海学院，西安 710072)

自由阻尼结构通常是在金属类刚性较大的结构上敷设一层起到阻尼作用的材料(粘弹材料为主)，这类结构被广泛应用在机舱壁、艇壳以及汽车薄壁和管道等结构中，用以提高结构的阻尼性能。自由阻尼结构是最简单的附加阻尼结构，由基底层和阻尼层两层结构构成。

经典的附加阻尼理论包括复刚度法及变形能法[1-5]。Oberst等[1]首先提出当自由阻尼结构简谐振动时，其弯曲刚度可被视为复数，虚部与实部之比就是结构的损耗因子。Kerwin和Ungar等[2-5]将复刚度理论推广到夹芯阻尼结构并提出能量概念，在振动为无衰减的简谐振动假设下，利用复刚度法和应变能法得到夹芯阻尼结构的损耗因子公式。遗憾的是，经典阻尼理论的损耗因子公式中都忽略了基底层的阻尼。而后，臧献国等[6,11]将应变能法应用到自由阻尼结构的厚度优化上，Sainsbury等[7]应用变形能法计算自由阻尼圆柱壳的阻尼，Lepoittevin等[8]则利用变形能与模态数据对约束阻尼结构进行优化设计。基于复刚度法的复模量测试及理论研究也在不断深入。

随着阻尼技术的发展，金属基阻尼合金、纤维增强型复合材料等新型材料被研制开发出来，这类材料不仅能具有良好的力学特性，本身也具有一定的阻尼减振能力。如阻尼合金BaTiO3/Al[9]、Mg-10Gd-6Y-xZn-0.6Zr[12]在低频时的损耗因子能达到0.02以上，武海鹏等[13]研究的玻璃纤维复合材料的损耗因子在0.01以上，洪暄清等[14]研究的纤维增强改性阻尼材料其损耗因子则可以高达0.1以上。若在此类新型复合材料上敷设粘弹阻尼材料，作为基底层的新型材料本身的阻尼特性不可忽略，经典的自由阻尼结构损耗因子公式不再适用。因此有必要针对基底阻尼较大的自由阻尼结构开展阻尼理论研究，对以往的结构损耗因子公式进行修正。

1 理论模型

1.1 变形能法损耗因子修正公式

根据变形能理论，自由阻尼结构的结构损耗因子为:

(1)

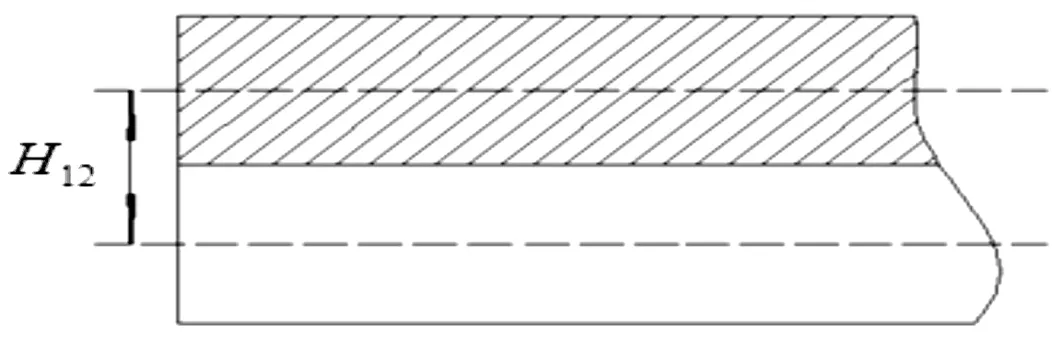
图1 自由阻尼结构截面图

图2 自由阻尼结构受力分析

(2)

设x处的角位移θ*(x)简谐变化，即

θ*(x)=θ*coskx

(3)

(4)

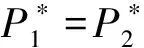
(5)

(6)

用αn表示各耗能子结构的拉伸损耗因子，βn表示各耗能子结构的剪切损耗因子，则

(7)

(8)

(9)

只考虑弯曲振动，结构单位长度的变形能包括三部分：拉伸变形能、弯曲变形能、剪切变形能。由于应变是关于位置x的函数，所以沿着轴向方向的变形能是不相等的，在全波长上的能量也是不同的。通常计算损耗因子需要在一定尺度内平均，将单位长度的能量在全波长λ=2π/k上积分并除以波长，就得到能量密度平均值，继而根据能量表达式求得损耗因子。

简谐振动情形下，拉伸变形能的能量密度可表示成

(10)

弯曲变形能的能量密度为

(11)

剪切变形能的能量密度为

(12)

根据损耗因子应变能公式，任意附加结构的结构损耗因子就可以用如下公式表示

(13)

式中:N表示系统有N个子结构，l表示有l个子结构耗损拉伸、弯曲变形能，m表示有m个子结构耗损剪切变形能。

进一步有

(15)

由力学关系可知弯曲刚度的实部与拉伸刚度的实部有如下

(16)

其中:rn是子结构n的中性面到原点的距离。

对于均匀梁板类结构，有如下几何关系

(17)

(18)

将上述几何关系代入式(15)可得:

(19)

经过化简并略去高阶小量，可最终得到考虑基底阻尼的自由阻尼结构损耗因子公式

(20)

式中:α1为基底层材料的拉伸损耗因子；α2为阻尼层材料的拉伸损耗因子。

实践中阻尼材料的拉伸损耗因子和剪切损耗因子非常接近，即阻尼层α2≈β，若忽略基底层阻尼，即α1=0，此时就能得到著名的自由阻尼结构损耗因子公式[4, 10]

(21)

1.2 复刚度法损耗因子修正公式

根据复刚度定义，将结构的复弯曲刚度表示为B*=B(1+iη)，η为结构损耗因子。

考虑自由阻尼结构的拉伸变形，根据经典复刚度法可得自由阻尼结构总的复弯曲刚度与基底层复弯曲刚度有如下比值关系[10]

(22)

从上式可以看出，复刚度比值与阻尼层、基底层的厚度比h及复杨氏模量比e*有关。

定义α1为基底层的材料损耗因子，α2为阻尼层的材料损耗因子，则式(22)变为

(23)

为方便计算，将复杨氏模量比e*表示为

(24)

将式(24)代入式(23)，取左右两边的实部和虚部分别相等，可得

(25)

(26)

由上式可得结构损耗因子修正公式

(27)

(28)

求出结构损耗因子η后，代入式(25)就能求得自由阻尼结构总的弯曲刚度。

2 分析讨论

2.1 两种修正公式对比

上述自由阻尼结构的两种理论都只考虑结构的弯曲振动，且假设角位移、轴向位移、剪切变形等均为简谐变化。在分析中均忽略了振动中的剪切变形，复刚度法只考虑了阻尼层和基底层的拉伸变形，而变形能法除此之外还考虑了各层结构的弯曲变形。比较变形能法的损耗因子修正公式(20)和复刚度法的损耗因子修正公式(27)，可以看出变形能法的修正公式更为简洁，更方便工程应用，而计算组合结构的总弯曲刚度时则可以利用复刚度法得到的修正公式(25)。

取自由阻尼结构基底层和阻尼层的材料损耗因子分别为α1=0.01,α2=0.5，阻尼层与基底层的杨氏模量比为e=10-3，利用复刚度法与变形能法的修正公式计算结构损耗因子，随厚度比变化的曲线如图3所示。

由仿真结果可见，复刚度法和变形能法修正公式所得的结构损耗因子曲线几乎重合，这说明在自由阻尼结构振动中，起耗能主导作用的是拉伸变形，弯曲变形和剪切变形均可忽略不计。分析二者的求解公式也知，复刚度法只比变形能法多出一些高阶小项，仿真结果说明这些高阶项影响不大，可忽略不计，所以两种方法的求解结果始终一致。

2.2 修正公式适用范围

取自由阻尼结构阻尼层的材料损耗因子为α2=0.5，阻尼层与基底层的杨氏模量比分别为e=10-3、e=10-4、e=10-5，利用变形能法修正公式(20)求解考虑基底阻尼情况下的结构损耗因子，利用经典公式(21)求解忽略基底阻尼情形下的结构损耗因子，当基底阻尼分别取为α1=0.001、α1=0.01时，对应的结构损耗因子仿真曲线分别如图4(a)、(b)所示，修正前后损耗因子的相对误差如图5(a)、(b)所示。

由仿真可以看出，当基底层阻尼较小时(α1<0.01)，对于厚度比大于1的自由阻尼结构，基底层阻尼可以忽略不计。但若基底层的材料阻尼很大(α1≥0.01)，在阻尼层与基底层的厚度比h较小时，忽略基底层阻尼将导致自由阻尼结构的损耗因子计算值偏小，引起很大的误差，且模量比e越小，基底层阻尼的影响越显著。此时应考虑基底层阻尼，必须应用损耗因子修正公式，修正公式对于一般的自由阻尼结构阻尼计算均适用。

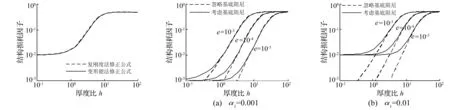
图3 两种修正公式得到的结构损耗因子曲线对比

图5 修正前后结构损耗因子的相对误差

3 仿真验证

利用ANSYS软件建立1.2 m×1.0 m自由阻尼矩形板的实体模型，各层的具体材料参数见表1，其中基底层材料有两种设置：钢材质和玻璃钢材质。阻尼层材料的阻尼参数有两种设置：损耗因子为定值0.5；动态阻尼特性如图6所示。进行谐响应分析后，提取输入功率以及自由阻尼结构各层的变形能，利用输入功率法和变形能法得到的计算结果对损耗因子修正公式进行仿真验证。修正公式解析解与有限元数值解的仿真对比如图7、8所示。

表1 自由阻尼结构各层材料参数

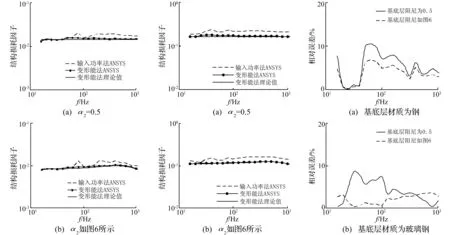
图7 基底层材质为钢的自由阻尼结构损耗因子曲线(α1=0.005)

由仿真与理论公式计算结果对比可以看出，无论是基底阻尼较小的钢还是基底阻尼较大的玻璃钢材料，变形能法修正公式的解析解均与有限元变形能法的数值解相吻合，相对误差不超过10%。由于输入点的振动响应随频率变化且略高于平均速度，输入功率法求得的有限元数值解高于变形能法的数值解，且随频率波动，但两种方法得到的损耗因子曲线趋势完全相同。

4 结 论

本文针对基底层阻尼较大的自由阻尼结构开展了阻尼理论研究。不同于经典阻尼公式，在应力分析中考虑了基底层的应变，而后分别利用变形能理论和复刚度理论推导得到修正的损耗因子公式。为了验证修正公式的正确性，利用ANSYS软件建立自由阻尼矩形板的实体模型并进行谐响应分析，分别利用变形能法和输入率法求得结构损耗因子的数值解。

通过两种修正公式的解析解与有限元数值解的对比，得出以下结论：

(1) 对于基底层材料损耗因子大于0.01的自由阻尼结构，在阻尼层与基层厚度比较小时忽略基底阻尼会导致组合结构的阻尼计算偏小，需要利用修正公式进行阻尼计算。

(2) 分析自由阻尼结构振动时，变形能法同时考虑了两层结构的拉伸变形和弯曲变形，复刚度法只考虑了拉伸变形，但两种损耗因子修正公式的解析解完全吻合，这说明自由阻尼结构的弯曲振动中起耗能主导作用的是拉伸变形，弯曲变形和剪切变形均可忽略不计。变形能法的损耗因子修正公式更为简洁明了，更方便工程应用。

(3) 无论阻尼层材料的阻尼为常值或呈现动态特性，对于基底材料不同的自由阻尼结构，修正公式的解析解与两种有限元数值解均一致，这证明了变形能法损耗因子修正公式是正确的，可用于一般基底层的自由阻尼结构计算。

[1] Oberst H, Frankenfeld K. Überdie dämpfung derbiegeschwingunge dünner bleche durch festhaftende bläge[J]. Akustische Beihefte, 1952, 2(4): 181-194.

[2] Kerwin E M. Damping of flexural waves by a constrained visco-elastic layer [J]. Journal of the Acoustical Society of America, 1959, 31: 952-962.

[3] Ross D, Ungar E E, Kerwin E M. Damping of plate flexural vibrations by means of visco-elastic laminae structural damping [J]. American Society of Mechanical Engineers, 1959: 49-87.

[4] Ungar E E. Loss factors of viscoelastically damped beam structures [J]. Journal of the Acoustical Society of Amenrica, 1962, 34(8): 1082-1089.

[5] Ungar E E, Kervwin E M. Loss factors of viscoelastic systems in terms of energy concept [J]. Journal of the Acoustical Society of Amenrica, 1962, 34(7): 954-958.

[6] Zang Xian-guo, Yu De-jie, Yao Ling-yun, et al. Optimaization of thickness distribution of unconstrained damping layer based on mode shapes [J]. Composite Structures, 2006, 74:63-69.

[7] Sainsbury M G, Masti R S. Vibration damping of cylindrical shells using strain energy based distribution of an add-on viscoelastic treatment [J]. Finite Elements in Analysis and Design, 2007, 43: 175-193.

[8] Lepoittevin G, Kress G. Optimization of segmented constrained layer damping with mathematical programming using strain energy analysis and modal data [J]. Materials and Design, 2010, 21:14-24.

[9] Fan Gen-lian, Li Zhu-qiang, Zhang Di, et al. Damping capacity of BaTiO3/Al composites fabricated by hot extrusion [J]. Transactions of Nonferrous Metals Society of China, 2012, 22:2512-2516.

[10] 戴德沛. 阻尼减振降噪技术[M]. 西安: 西安交通大学出版社, 1986.

[11] 臧献国,于德介,姚凌云,等. 基于模态振型的自由阻尼层厚度分布优化[J]. 中国机械工程, 2010, 21(5): 515-518.

ZANG Xian-guo, YU De-jie, YAO Ling-yun, et al. Optimization of thickness distribution of unconstrained damping layer based on mode shape [J]. China Mechanical Engineering, 2010, 21(5): 515-518.

[12] 宋鹏飞,王敬丰,周小蒽,等. Zn 含量对Mg-10Gd-6Y-xZn-0.6Zr合金显微组织、力学和阻尼性能的影响[J]. 中国有色金属学报, 2012, 22(9): 2430-2438.

SONG Peng-fei, WANG Jing-feng, SONG Xiao-en, et al. Effects of Zn content microstructure, mechanical properties anddamping capacities of Mg-10Gd-6Y-xZn-0.6Zr alloys [J]. The Chinese Journal of Nonferrous Metals, 2012, 22(9): 2430-2438.

[13] 武海鹏,侯涤洋,孙立娜,等. 玻璃纤维、碳纤维复合材料的阻尼性能分析[J]. 应用力学学报, 2012, 29(1): 65-69.

WU Hai-peng, HOU Di-yang, SUN Li-na, et al. Damping analysis of glass and carbon fiber composites [J]. Chinese Journal of Applied Mechanics, 2012, 29(1): 65-69.

[14] 洪暄清,王旭升,姚熹,等. 纤维增强改性阻尼材料研究[J]. 材料导报: 研究篇, 2012, 22(9):125-128.

HONG Xuan-qing, WANG Xu-sheng, YAO Xi, et al. Investigation on the damping properties of fiber-reinforced composites [J]. Materials Review: Research, 2012, 22(9): 125-128.