希尔伯特振动分解在滚动轴承故障诊断中应用

朱可恒，宋希庚，薛冬新

(大连理工大学 能源与动力学院,辽宁 大连 116023)

滚动轴承作为旋转机械常用部件，其运行状态可决定整台机器性能，故滚动轴承状态监测与故障诊断均为研究热点[1-3]。机械故障诊断方法之一为对机械设备振动信号进行分析。滚动轴承出现故障时，振动信号呈非平稳、非线性特征，传统傅里叶变换对此类信号分析存在较大局限性。小波变换具有的多分辨率特性非常适合处理非稳态信号，广泛应用于旋转机械故障诊断[4]。小波基一旦选定，在整个分析过程中无法更换，不同基函数会对分析结果产生较大影响[5]。经验模式分解(Empirical Mode Decomposition, EMD)[6]为非平稳信号处理方法，可据信号局部时变特征进行自适应分解，因而获得广泛应用[7-8]。EMD方法缺限在于分解过程中拟合上下包络线引起的端点效应[9]及由于异常事件引起的模态混叠[10]。

机械振动非平稳信号处理方法由Feldman[11]提出，并取名希尔伯特振动分解(Hilbert Vibration Decom-position, HVD)。刘慧等[12-13]将HVD方法用于电压闪变检测及非整数次谐波检测，取得较好效果，即利用希尔伯特变换获得解析信号，通过低通滤波及同步检波获得幅值最大分量，通过迭代运算按幅值大小自适应分解出相应分量。HVD较EMD，既保留分解自适应性又避免样条拟合，运算效率及分辨率更高[14-15]。本文将HVD方法用于滚动轴承故障诊断。用HVD方法对EMD因异常事件引起的模态混叠现象仿真分析，发现HVD能分解出不同模态，采用波形匹配方法[9]消除希尔伯特变换与低通滤波引起的端点效应；将HVD用于滚动轴承故障信号分解，结合包络解调分析轴承故障特征频率，识别故障发生位置。仿真分析及实验结果验证HVD方法的有效性。

1 HVD方法[11]

该方法为将复杂非稳态信号分解为幅值大小不同的分量之和，对信号x(t) 具体分解步骤为：

(1) 估计幅值最大分量瞬时频率。以两分量信号为例，即

(1)

通过希尔伯特变换求得瞬时频率为

ω(t)=ω1+

(2)

式(2)含两部分，即瞬时频率ω1与快速变化不对称振荡频率。可以证明[11]，a1大于a2时，对后者在区间[0T=2π/(ω2-ω1)] 上定积分结果为0。即幅值最大分量瞬时频率ω1可通过ω(t) 估计获得。实际中可用低通滤波去除不对称振荡部分获得ω1。考虑一般情况，x(t) 由更多分量组成，瞬时频率ω表达会更复杂，但用低通滤波仍能提取幅值最大分量的瞬时频率[11]。

(2) 利用同步检波求出相应瞬时幅值及相位。同步检波即通过初始信号与两参考正交信号相乘提取频率已知分量幅值。以估计的瞬时频率为参考频率ωr，获得同相输出为

xl=r(t)=

cos(∫(ωl(t)+ωr(t))dt+φl(t))]

(3)

正交相输出为

sin(∫[ωl(t)+ωr(t)]dt+φl(t))]

(4)

式(3)、(4)均含两部分，与参考频率不相同分量与第一部分产生无关。通过低通滤波去掉后半部分，得相应表达式为

(5)

(6)

由式(5)、(6)可得瞬时幅值

(7)

瞬时频率为

(8)

(3) 通过上两步可提取幅值最大分量(x1(t))，用初始信号减去x1(t)，得

xl-1(t)=x(t)-x1(t)

(9)

将xl-1(t)作为新初始信号，重复以上两步依次获得不同幅值分量。两连续迭代结果标准差满足一定条件时停止迭代。低通滤波为HVD算法关键，截止频率选择决定HVD 频率分辨率。考虑波形失真及滤波器稳定前提下，为分解出频率相近分量，截止频率应小于相邻分量频率差值；为让分解的每个分量瞬时频率有本质变化(不为常数)，截止频率不能无限小[14]。

2 仿真分析

用HVD方法分析分量频率相近及由异常事件引起EMD模态混叠的仿真信号发现，HVD方法能将信号有效分解开。其中异常事件主要包括间断信号及脉冲干扰[10]。

2.1 基于波形匹配的端点延拓

HVD算法中希尔伯特变换与低通滤波器对截断数据进行处理均会产生端点效应，影响分解精度，且误差通过迭代运算累积不断增大[12]。考虑滚动轴承故障信号的近似周期性，本文采用基于波形匹配的自适应端点延拓方法[9]消除端点效应。该方法通过计算波形匹配度寻找信号内部与边缘处变化趋势最相似子波，利用该子波对原始信号进行延拓，具有自适应性。

为显示端点延拓后效果，以仿真信号为例说明：

x(t)=2sin(2πt)+10sin(3πt)

(10)

未经端点延拓处理的HVD分解结果(为方便，只选前两分量)见图1，图中c1，c2分别代表分解出的前两个分量，可见在端点处均出现严重失真。经延拓处理后HVD分解结果见图2。由图2看出，端点效应已消除，能真实反映信号中所含两分量。

2.2 分量频率相近信号HVD分解

EMD不能有效分解频率比值在[0.5 2]间分量，而将其作为单个调制信号[16]。仍采用式(10)仿真信号，EMD分解只能获得一个分量，见图3，图中x(t)为被分解信号，IMF为EMD分解结果。与图2对比看出，HVD较EMD频率分辨率更高。

2.3 含间断信号的HVD分解

仿真信号为在幅值1的低频正弦中加入两相同频率的高频正弦，间断成分幅值为0.2，见图4、图5中x(t)，其中c1，c2及IMF1，IMF2分别为HVD与EMD分解的前两分量。由两图看出，HVD能成功分解出包含在信号中的间断分量c1，而IMF1不仅含部分低频正弦信号，亦含高频间断信号，出现频率混叠。

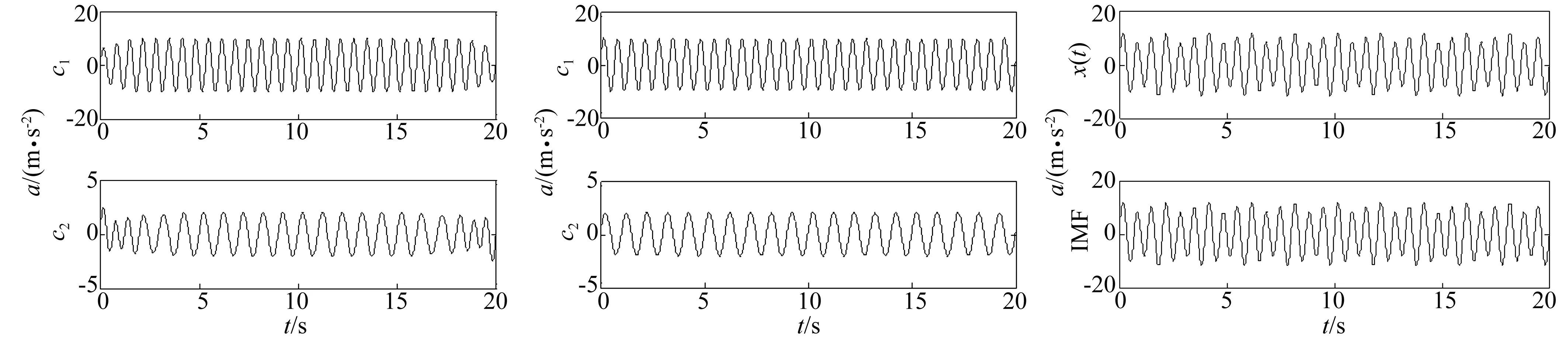
图1 端点无延拓HVD分解结果

图4 含间断信号的HVD分解结果

2.4 含脉冲信号的HVD分解

仿真信号为在幅值1的低频正弦中加入正负各0.5脉冲，见图6、图7中x(t)，其中c1，c2及IMF1，IMF2分别为HVD及EMD分解的前两分量。由两图看出，EMD分解结果模态混叠明显，HVD虽未分解出脉冲信号，但分解获得低频正弦分量，亦未现混叠现象。

综合以上分析，对分量频率相近信号、含间断信号或脉冲信号的信号，HVD具有较EMD更好的分解效果，反映系统本质更准确。

3 基于HVD方法的滚动轴承故障诊断步骤

鉴于HVD较EMD频率分辨率更高，且能有效分解出EMD方法中易引起模态混叠信号，本文将HVD引入滚动轴承振动信号分解，结合包络分析进行故障诊断，具体故障诊断步骤为：① 获取滚动轴承正常及内外圈故障状态振动信号；② 对每种状态振动信号进行HVD分解；③ 考虑滚动轴承出现故障时振动冲击所致幅值较大，故障信息主要包含在HVD分解的第一分量中，因此选第一分量进行包络谱分析；④ 据包络谱识别轴承故障特征频率并诊断。

4 实验信号分析

4.1 实验数据

据实验数据[17]，以驱动端轴承型号为例，SKF6205型号轴承基本参数见表1、表2。选转速1 797 r/min、负荷为零的内、外圈故障数据进行分析。采样频率12 kHz，旋转频率为fr=29.95 Hz。由表2计算内圈故障频率为finner= 162.1 Hz，外圈故障频率为fouter=107.4 Hz。

表2 SKF6205通过特征频率

4.2 内圈故障信号分析

x(t)，c1分别为内圈故障时时域波形及HVD分解的第一分量见图8。由图8看出，虽内圈故障表面与其它零件撞击造成的冲击明显，但不能由此确定轴承故障发生位置；且内圈故障点离振动信号测量点较远，相对位置不固定，传递路径更复杂，因此滚动轴承内圈故障诊断相对较难。

图8 内圈故障信号与HVD分解第一分量

对内圈故障信号进行HVD分解，取含丰富故障信息的第一分量c1作希尔伯特变换获得包络信号后再作谱分析获得包络谱(频率大于600 Hz幅值均较小，为显示清楚，只取600 Hz以内谱图)，见图9。由图9可清晰看出内圈故障特征频率(finner= 161.1 Hz,接近理论计算值162.1 Hz)、转频及高倍转频。

图9 内圈故障HVD分解第一分量包络谱

4.3 外圈故障信号分析

图10 外圈故障信号与HVD分解第一分量

滚动轴承外圈一般固定在轴承座上，与振动信号测点间位置相对固定，故滚动轴承外圈故障诊断相对较易。外圈故障信号x(t) 与其对应的HVD分解第一分量c1时域波形见图10。对外圈故障信号进行HVD分解，取含丰富故障信息的第一分量c1作希尔伯特变换，获得包络谱(取600 Hz以内谱图)见图11。由图11可清晰看出外圈故障特征频率(fouter= 108.4 Hz，接近理论计算值107.4 Hz)、高倍频及转频。

图11 外圈故障HVD分解第一分量包络谱

5 结 论

(1) 本文提出的基于希尔伯特振动分解(HVD)的滚动轴承故障诊断新方法，先通过希尔伯特变换求出信号瞬时频率，再利用低通滤波及同步检波获得初始信号中幅值最大分量，通过迭代运算逐步分解出剩余分量，具有自适应性。

(2) 与EMD相比，HVD方法能避免样条拟合及复杂的分解过程，运算效率更高。仿真分析表明HVD方法能有效分解引起EMD模态混叠的含异常事件信号，且频率分辨率更高。实验信号分析表明，本文所提方法对轴承故障诊断具有效性，能准确识别滚动轴承内、外圈故障。

[1] 赵志宏，杨绍普.一种基于样本熵的轴承故障诊断方法[J].振动与冲击，2012，31(6): 136:141.

ZHAO Zhi-hong, YANG Shao-pu.Sample entropy-based roller bearing fault diagnosis method[J].Journal of Vibration and Shock, 2012, 31(6): 136-141.

[2] 李辉，郑海起，杨绍普.基于EMD和Teager能量算子的轴承故障诊断研究[J].振动与冲击，2008, 27(10):15-17.

LI Hui, ZHENG Hai-qi, YANG Shao-pu.Bearing fault diagnosis based on EMD and Teager-Kaiser energy operator[J].Journal ofVibration and Shock, 2008, 27(10): 15-17.

[3] 李常有,徐敏强,高晶波,等.基于独立分量分析的滚动轴承故障诊断[J].哈尔滨工业大学学报,2008,40(9): 1363-1365.

LI Chang-you, XU Min-qiang, GAO Jing-bo, et al.Fault diagnosis for rolling element bearings based on independent component analysis[J].Journal of Harbin Institute of Technology, 2008,40(9): 1363-1365.

[4] 赵志宏,杨绍普.基于小波包变换与样本熵的滚动轴承故障诊断抗[J].振动、测试与诊断,2010, 29(4): 640-644.

ZHAO Zhi-hong, YANG Shao-pu.Roller bearing fault diagnosis based on wavelet packet transform and sample entropy[J].Journal ofVibration,Measurement & Diagnosis, 2010, 29(4): 640-644.

[5] 于德介,程军圣,杨宇.机械故障诊断的Hilbert-Huang变换方法[M].北京：科学出版社,2006.

[6] Huang N E, Shen Z, Long S R, et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceeding of Royal Society London, 1998,454 (1971): 903-995.

[7] 张琳，黄敏.基于EMD与切片双谱的轴承故障诊断方法[J].北京航空航天大学学报,2010, 36(3): 287-290.

ZHANG Lin, HUANG Min.Fault diagnosis approach for bearing based on EMD and bi-spectrum[J].Journal of Beijing University of Aeronautics and Astronautics,2010,36(3):287-290.

[8] 苏文胜,王奉涛,张志新,等.EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J].振动与冲击,2010,29(3):18-21.

SU Wen-sheng, WANG Feng-tao, ZHANG Zhi-xin, et al.Application of EMD denoising and spectral kurtosis in early fault diagnosis of rolling element bearings[J].Journal of Vibration and Shock, 2010, 29(3):18-21.

[9] 邵晨曦,王剑,范金锋,等.一种自适应的EMD端点延拓方法[J].电子学,2007,35(10): 1944-1948.

SHAO Chen-xi, WANG Jian, FAN Jin-feng, et al.A self- adaptive method dealing with the end issue of EMD[J].Acta Electronic Sinica, 2007, 35(10):1944-1948.

[10] 胡爱军，孙敬敬，向玲.经验模态分解中的模态混叠问题[J].振动、测试与诊断,2011,31(4): 429-436.

HU Ai-jun, SUN Jing-jing, XIANG Ling.Mode fixing in empirical mode decomposition[J].Journal of Vibration, Measurement &Diagnosis, 2011, 31(4): 429-436.

[11] Feldman M.Time-varying vibration decomposition and analysis based on the Hilbert transform[J].Journal of Sound and Vibration, 2006, 295(3/5): 518-530.

[12] 刘慧,刘国海,沈跃.采用希尔伯特振动分解的非整数次谐波检测新方法[J].高压电技术，2009, 35(7): 1758-1764.

LIU Hui, LIU Guo-hai, SHEN Yue.Novel method for Non- integer harmonics measuremet using hilbert vibration decomposition[J].High Voltage Engineering, 2009, 35(7): 1758-1764.

[13] 刘慧，刘国海，沈跃.基于希尔伯特振动分解的电压闪变检测新方法[J].仪器仪表学报,2009,30(9): 2001-2006.

LIU Hui, LIU Guo-hai, SHEN Yue.Novel method for detection of voltage flicker based on hilbert vibration decomposition[J].Chinese Journal of Scientific Instrument, 2009, 30(9): 2001-2006.

[14] Feldman M.Theoretical analysis and comparison of the Hilbert transform decomposition methods[J].Mechanical Systems and Signal Processing, 2008, 22(3): 509-519.

[15] Braun S, Feldman M.Decomposition of non-stationary signals into varying time scales: Some aspects of EMD and HVD methods[J].Mechanical Systems and Signal Processing, 2011, 25(7): 2608-2630.

[16] Deering R, Kaiser J F.The use of a masking signal to improve empirical mode decomposition[J].IEEE International Conference on Acoustics, Speech, and Signal Processing, 2005, 4: 485-488.

[17] The case western reser ve univer sity bearing data center[EB/OL].[2012-11-01].http://csegroups.case.edu/ Bearing Data Center/pages/download-data-file.