钢筋混凝土粘结-滑移率敏感性研究进展

张 艳 波

(同济大学土木工程学院，上海 200092)

钢筋混凝土粘结-滑移率敏感性研究进展

张 艳 波

(同济大学土木工程学院，上海 200092)

总结了国内外大量有关钢筋混凝土粘结应力-滑移性能率敏感性研究的文献，系统地介绍和分析了试验研究领域内钢筋混凝土粘结性能率敏感性研究的成果。在此基础上，针对钢筋混凝土粘结应力-滑移性能率敏感性研究中的一些基本问题，提出了开展进一步研究工作的方向，以求更好的理解和掌握粘结应力-滑移性能。此外，还介绍了目前用于动力试验研究的3种试验装置。

加载速率；粘结应力-滑移；粘结性能；率敏感性；试验装置

0 引言

粘结应力-滑移本构方程是钢筋混凝土结构理论基本方程之一。通过粘结作用，可以实现钢筋和混凝土之间的荷载传递和协调变形。粘结性能的退化和丧失必然导致结构力学性能的降低甚至破坏[1]。粘结应力-滑移性能对结构或构件的承载能力、钢筋锚固或搭接、裂缝宽度和间距、节点的转动等计算有重要影响[2]。我国《混凝土结构设计规范》GB50010[3]也明确规定：某些变形较大的构件或节点进行局部精细分析时，宜考虑钢筋和混凝土之间的粘结-滑移本构关系，并给出了钢筋与混凝土的粘结应力-滑移本构关系的分段式方程，为结构大变形时进行更精确的分析提供了界面粘结-滑移参数。

钢筋混凝土结构在其服役期内，除承受静荷载外，不可避免地遭遇地震荷载、爆炸、冲击等动力作用，特别是核电站、海岸工程、公路栅栏等结构。此时，结构往往在很短的时间内就进入非线性阶段，结构或构件的应变率很大，结构的力学响应与静荷载下有很大不同。传统的线弹性设计分析方法受到严峻挑战，这促使了结构非线性分析理论的发展。

钢筋混凝土结构非线性分析的核心问题是本构的研究。混凝土的多轴动力本构关系及其破坏准则和动力荷载下钢筋与混凝土之间粘结应力-滑移本构关系是结构非线性分析的两大难点。在用有限元软件进行精细的结构非线性分析时，也需要确定钢筋与混凝土界面粘结-滑移参数，因为非线性分析中钢筋混凝土单元刚度矩阵与粘结性能密切相关[4]。可见，动力粘结-滑移本构方程的研究是进行结构非线性分析的重要环节之一。

动力荷载下粘结性能的研究主要可以划分为2个方面：(1)单调荷载下，加载速率对粘结性能的影响；(2)反复和重复荷载下，粘结性能的损伤退化研究。国内外学者已经对后者进行了大量的试验研究和理论分析，并取得了丰硕的成果，但是关于粘结性能加载速率敏感性研究的文献，相对来说还比较少[1]。由于试验条件的不同、影响因素的多样性、粘结机理的复杂性等原因，粘结滑移性能的率相关性研究至今仍没有一个公认的研究成果。

随着钢筋混凝土结构非线性分析和结构设计软件的发展，对结构分析的要求越来越高，特别是进行结构抗震设计时，粘结应力-滑移力学参数已经成为结构设计中的瓶颈，制约了结构分析和设计理论的发展[5]。因此，充分认识粘结应力-滑移性能的率敏感性，建立动力粘结强度和粘结-滑移本构方程，对结构分析和设计具有重要意义。

1 动力粘结-滑移试验装置

由于粘结机理的复杂性、影响因素的多样性等，从理论上进行粘结-滑移性能的分析难度较大，所以粘结性能的研究主要集中在试验研究领域，特别是粘结性能的率敏感性研究。高加载速率主要通过以下3种试验装置获得[6]。

1.1MTS万能试验机

MTS万能试验机一般用于岩石和混凝土的材性试验，见图1。通过合理设计，同样可以用于动力粘结试验。万能试验机虽然测量精度比较高，但能够获得的加载速率一般比较小，以同济大学的MTS815万能试验机为例，能够获得的加载速率最高为30 mm/s，基本可以实现地震荷载对应的材料应变速率。

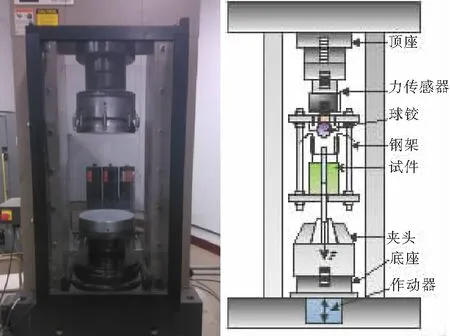
图1 万能试验机装置

1.2落锤试验

试验时通过安装在锤头的力传感器测量打击力，位移则通过安装在锤头的加速度传感器和安装在底座上的位移传感器测量，见图2。应当指出，落锤试验虽然是一种高速加载试验方法，但是锤头打击试件时，由于应力波传播弥散效应，试件中的应变分布不均匀，试验中位移或应变的测量也会有较大的误差。这种试验方法可以定性地比较动静荷载下的粘结应力-滑移性能，系统地研究加载速率对粘结滑移性能的影响时，不容易控制和测量加载速率。

图2 落锤试验装置

1.3分离式霍普金森压杆(SHPB)试验

分离式霍普金森压杆是一种在动力试验中广泛应用的试验装置，见图3。这种装置利用应力波使试件在高应变率条件下受力，并采用一维波动理论分析混凝土试件的受力状态。很多学者已经将这种试验装置应用于动力粘结性能的研究。利用这种装置可以获得高速加载下拉拔力-滑移关系全曲线，可以有效地消除应力波的弥散效应，但是受试验设备的限制，试件的尺寸一般比较小。

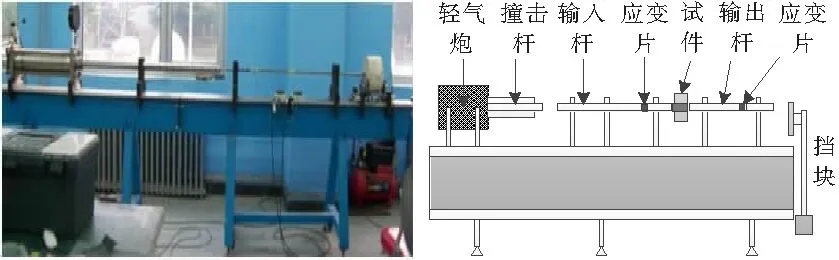
图3 分离式霍普金森压杆试验装置

2 试验研究成果

1962年美国学者Robert J Hansen[7]等对动荷载下钢筋与混凝土的粘结性能进行了拉拔试验研究。试验采用圆柱体短锚拉拔试件，螺纹变形钢筋直径为12.5 mm，钢筋位于试件中心，粘结长度为50 mm。此外混凝土圆柱体中绑扎了螺旋钢筋，这其实对混凝土提供了附加的横向约束，使得粘结锚固性能比真实情况提高了。试验结果表明：光圆钢筋与混凝土之间的粘结性能对加载速率不敏感，且试件多为钢筋刮出式破坏；变形钢筋与混凝土之间的粘结强度在动力荷载下则有明显提高，并且混凝土的强度越低、钢筋直径越小，粘结强度在动力荷载下提高的幅度越大。

虽然Robert J Hansen得到了变形钢筋与混凝土之间粘结强度随加载速率提高而提高的定性结论，但是对于提高的程度并没有给出量化的分析，难以在实际结构分析和设计中应用。

1982年E Vos和Reinhardt[2,8]通过采用分离式霍普金森压杆技术，试验研究了加载速率对钢筋、预应力绞线与混凝土之间粘结性能的影响。试验采用短锚拉拔试件，分别取加载速率、混凝土强度和钢筋类型为研究变量。作者采用了多种加载速率：0.3 MPa/s、80 MPa/s、(2～4)×104MPa/s、(1～1.6)×105MPa/s。这里的加载速率指平均粘结应力的加载速率，由试验数据反算得到。试验得到了与Hansen类似的结论：光圆钢筋、预应力绞线与混凝土之间的粘结强度对加载速率不敏感；随着加载速率的提高，变形钢筋与混凝土之间的粘结强度明显提高，且混凝土强度越低，粘结强度随加载速率提高的幅度越大。

通过对试验数据进行回归分析，E Vos给出了考虑加载速率影响的粘结强度表达式：

(1)

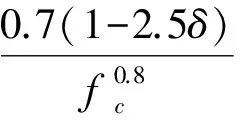
(2)

1992、1994年Cheng Yan[9,10]等通过落锤试验研究了冲击荷载下钢筋与混凝土之间的粘结性能。试件尺寸为152.4 mm×152.4 mm×63.5 mm，直径为11.3 mm的钢筋位于试件中心，粘结长度为63.5 mm。为了防止发生劈裂破坏，粘结区段内设置了2个螺旋箍筋，直径分别为63.5 mm和127 mm。为了更加精确的分析钢筋受力与粘结应力，在粘结区段的钢筋上开槽贴应变片。在给定的3种加载速率下，粘结强度随着加载速率的提高而提高，提高的幅度为30%～50%；加载速率提高时，粘结区段的粘结应力分布变得越不均匀。

与以往很多研究者得到的结论不同，本试验结果表明，较普通混凝土而言，高强混凝土对粘结性能的率敏感性影响更大。

2001年洪小健[11,12]等进行了加载速率对锈蚀钢筋与混凝土粘结强度影响的试验研究。试验采用半梁式构件，构件长320 mm，截面宽度150 mm、截面高度250 mm，内部实际粘结锚固区长度为120 mm，钢筋内部贴片处理。采用3种不同加载速率：10 kN/min、50 kN/s、500 kN/s。动荷载作用下，粘结破坏具有瞬时性，一般在0.1-1 s，破坏形态的一个显著特点是构件表面裂缝宽度较静载细窄，且加载速率越大裂缝越窄。试验结果表明，粘结强度随加载速率提高而提高，洪小健将这一现象归因于以下两点：(1)混凝土材料的动力特性；(2)应变滞后效应。

洪小健在对试验数据回归分析的基础上，给出了考虑锈蚀率、加载速率影响的极限粘结强度表达式：

(3)

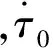
2003年Weathersby[13]试验研究了加载速率、横向约束、钢筋直径和外形对钢筋混凝土粘结性能的影响。试验采用圆柱体拉拔试件，粘结长度为254 mm，保护层厚度为127 mm和254 mm。钢筋直径为16 mm和20 mm。试验表明，对于所有的试件，破坏荷载均随加载速率的提高而提高，钢筋直径、外形及保护层等条件的不同，动峰值荷载较静力荷载提高的幅度也不同，从70%到100%不等。

2010年George[14]等采用分离式霍普金森压杆技术，进行了加载速率对钢筋与混凝土粘结性能的试验研究。试件的尺寸符合RILEM规范，圆柱体试件的直径为D=100 mm，钢筋直径为d=20 mm，屈服强度和极限强度分别为885 MPa和1 080 MPa。混凝土强度等级为C30/50。粘结长度分别为100 mm和200 mm。为了消除端部效应，两端各用50 mm长的PVC套管将钢筋和混凝土隔离开来，形成无粘结区。加载速率估计在100～250 MN/s。

试验得到了静力及动力荷载下拉拔力-滑移关系全曲线。试件主要有2种破坏形态：混凝土劈裂破坏和钢筋拔出破坏。由全曲线可以看出：动力拉拔荷载-位移曲线均位于对应的静力曲线之上，这说明粘结性能随着加载速率的提高而有所提高，在给定试验条件下，对于无约束试件，动力粘结强度可以提高90%以上，且混凝土强度越低，粘结强度提高的幅度越大。

河海大学的郑晓燕[15～17]等通过不同频率的三角波加载，试验研究了加载速率、锈蚀程度、锚固长度等对钢筋与混凝土之间动态粘结滑移性能的影响，初步探究了动荷载下锈蚀钢筋与混凝土的粘结机理，同样得到粘结应力随加载速率提高而提高的结论，另外还指出粘结刚度也有所提高，粘结应力分布变得更不均匀。

2012年Dongming Yan[18]等通过拉拔试验专门研究了加载速率对钢筋与普通混凝土之间粘结性能的影响。试件采用32.5R级波特兰水泥，混凝土抗压强度为35.9 MPa，标准差为1.52 MPa。采用圆柱体短锚试件，直径为203 mm，高165 mm，真正的粘结长度为63.5 mm。钢筋直径为15.9 mm。受试验机加载能力的限制，试验采用了4种位移加载速率：0.254 mm/min、2.54 mm/min、25.4mm/min和99.1 mm/min。数据采集频率为250 Hz。

试验得到了不同加载速率下粘结应力-滑移关系全曲线和峰值荷载-加载速率曲线，如图4、图5所示。

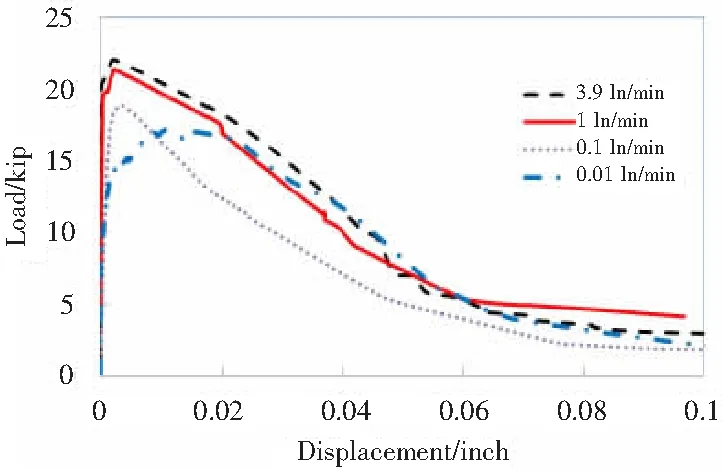
图4 不同加载速率下粘结-滑移曲线

图5 峰值荷载-位移对数关系曲线

由全曲线可以看出，不同加载速率下曲线的上升段非常接近；峰值拉拔荷载随着加载速率的提高而有所增大；峰值荷载所对应的位移随加载速率的增大而减小；粘结能，即力-荷载曲线与横轴所围面积，也随着加载速率的提高而提高，这说明结构或构件的耗能性能有所改善。

通过对试验数据进行回归分析，提出了一个峰值荷载-位移对数的关系式:

fbond=0.86ln(ε)+21.0

(4)

2013年Wei Yao[19]等采用改进的分离式霍普金森压杆技术，通过推出试验研究了加载速率和有效粘结长度对钢筋与混凝土之间粘结滑移性能的影响，试验结果如图6所示。

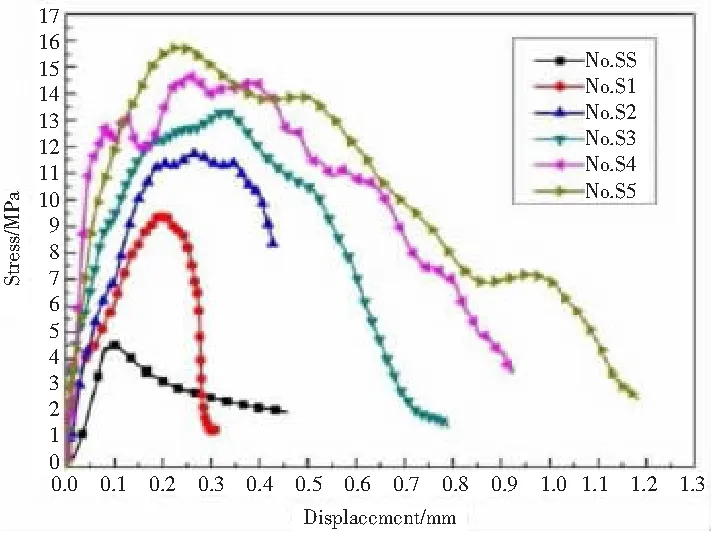
图6 粘结应力-滑移关系曲线

显而易见，随着加载速率的提高，峰值推出力和粘结强度均有所提高；峰值荷载所对应的滑移也随加载速率的提高而增大。

2004年M Alavi-Fard[20]等通过一些系列拉拔试验研究了加载速率对钢筋与高强混凝土间粘结性能的影响。钢筋直径为35 mm，保护层厚度为105 mm，粘结长度为100 mm。采用的加载速率分别为0.015 1 mm/min、1.51 mm/min、75 mm/min。试验所得的拉力-滑移荷载全曲线如图7所示。

图7 不同加载速率下的粘结应力-滑移曲线

可以看出，不同加载速率下峰值粘结强度和粘结应力-滑移关系曲线形状基本相同；不同加载速率下钢筋与高强混凝土之间的粘结强度基本不变，这与大部分的研究成果相左。笔者认为，本试验所用混凝土为高强混凝土，而高强混凝土强度和刚度的率敏感性不如普通混凝土，高强混凝土对粘结性能影响的率敏感性也不如普通混凝土，所以可能导致在加载速率也不是很大的情况下，粘结强度提高的幅度不明显。

此外，一些学者研究了加载速率对各种纤维与混凝土基体之间粘结性能的影响。比如，1995年Pacios[21]通过拉拔试验研究了加载速率对纤维和混凝土界面粘结性能的影响，位移控制加载速率为0.000 13～1 360 mm/s。试验得到了拉拔荷载-滑移关系全曲线。容易看出，动力荷载下力-滑移曲线均位于静力曲线之上，峰值拉拔荷载及对应的滑移随加载速率的提高而提高。Dong[22]等、Bindiganavile[23]和Taher[24]等分别通过试验研究了钢纤维与混凝土之间粘结性能的率相关性。三者均采用万能试验机位移控制加载，虽然在钢纤维类型、混凝土强度以及加载速率上不尽相同，但三者均得到了类似的结论：钢纤维与混凝土之间的粘结性能具有明显的率敏感性，特别是带肋和扭曲形钢纤维。Dong还引入了拉拔能的概念来描述加载速率对钢纤维和混凝土粘结性能的影响。Bindiganavile特别指出加载速率提高时，峰值荷载对应的裂缝宽度有所减小，即粘结刚度强化。

2006年George[25]等采用霍普金森压杆技术，试验研究了动力荷载下植筋与混凝土之间的粘结性能。结果表明，动力荷载下钢筋的锚固力随着加载速率的提高而提高，在该试验条件下提高约67%。作者将这一现象归因于钢筋与混凝土材料的动力特性。另外，国内的李艳茹[26～28]等分别通过动力粘结试验和有限元分析，也同样得到动力荷载下钢筋锚固力提高的结论。

纤维、植筋与混凝土之间动力粘结性能的研究对于钢筋混凝土粘结性能的率敏感性研究具有一定的借鉴意义。

3 粘结-滑移性能率敏感性研究基本

问题

3.1粘结强度

粘结强度是粘结滑移理论的一个重要概念。粘结强度直接影响着结构或构件能够传递的最大荷载。上述文献基本都集中在粘结强度的研究。由于试验条件的不同，粘结强度率敏感性程度的离散性很大，但研究者普遍认为：对于变形钢筋，粘结强度随着加载速率的提高而提高；混凝土的强度越低，粘结强度的率敏感性越明显。个别研究者却得到了相反的结论，如M Alavi- Fard[20]等在研究高强混凝土与钢筋粘结性能的率敏感性时，就得到加载速率对钢筋与高强混凝土间粘结强度影响不大的结论，Cheng Yan[9,10]等通过试验得到了高强混凝土越高，粘结性能率敏感性越明显的结论等。对此矛盾，需要开展进一步深入的研究。

3.2粘结-滑移本构关系

粘结滑移本构关系是粘结滑移理论核心问题。在进行结构非线性分析、大变形计算以及有限元分析时，都需要知道钢筋与混凝土界面动力粘结-滑移参数。

静力粘结-滑移本构方程的研究，在试验研究和理论分析方面都取得了很大进展。比较典型的如Nilson[29]、Mirza和Houde[30]、Eligehausen[31]等、徐有邻[32]等在试验研究的基础上，提出了局部粘结-滑移本构方程；Tepfers[33]、高向玲[34]等、Huanzi Wang[35]等从理论分析的角度给出了局部粘结-滑移本构方程。但是对于粘结应力-滑移率本构方程的研究至今仍然空白。虽然很多研究者都通过动力粘结试验得到了粘结应力-滑移关系全曲线，但很少看到研究者对粘结-滑移率本构方程进行研究。

混凝土强度是影响粘结性能的主要因素，进行粘结-滑移率敏感性研究必须考虑混凝土的动力特性。另外，混凝土的率本构研究方法对粘结-滑移率本构的研究有一定的借鉴意义。

3.3拉拔能

拉拔能，也称粘结能，是描述粘结性能好坏的一个重要指标。拉拔能指拉拔荷载-滑移全曲线与横轴所围的面积。Dongming Yan[18]、Dong Joo Kim[22]等都提到了拉拔能的概念。粘结能的大小，标志着结构或构件粘结耗能的大小，粘结能越大，说明结构或构件可以传递更大的荷载，或可以发生较大的变形，提高了结构或构件的延性。一般认为，加载速率提高时，粘结刚度增大，粘结-滑移曲线位于对应静力曲线之上，粘结能增大，而且幅度远大于粘结强度的提高幅度。

影响拉拔能大小的特征值是粘结强度、粘结强度对应的峰值位移以及粘结破坏时的滑移值等。大多数研究者认为峰值粘结应力对应的滑移随加载速率的提高而减小，个别研究者却持相反的观点[19]，对此也应开展进一步深入研究。

4 结论

本文总结和讨论了加载速率对钢筋与混凝土粘结性能影响的研究成果，主要得到以下结论。

(1)目前用于动力粘结应力-滑移性能研究的试验装置有：伺服万能试验机(MTS)、落锤试验机(Drop Weight Test)以及分离式霍普金森压杆(SHPB)试验装置。

(2)钢筋混凝土粘结应力-滑移性能具有明显的率敏感性：粘结强度随加载速率提高而提高，混凝土强度越低，粘结性能的率敏感性越强。

(3)为了更好的研究粘结-滑移率敏感性，建议考虑钢筋和混凝土材料的率本构关系，并开展进一步的试验研究和理论分析。

(4)可以尝试从损伤力学、断裂力学等力学知识和粘结能等能量观点从理论上研究粘结机理和粘结-滑移率敏感性本构关系。

[1] 江见鲸.高等混凝土结构理论[M].北京:中国建筑工业出版社,2010.

[2]Vos E,Reinhardt H W.Influence of loading rate on bond behavior of reinforcing steel and prestressing strands[J].Material and Construction,1982,15(1):3-10.

[3]GB50010-2010.混凝土结构设计规范[S].

[4]何 政,欧进萍.钢筋混凝土结构非线性分析[M].哈尔滨:哈尔滨工业大学出版社,2007.

[5]蔡传国,杨绪普,韦忠瑄.钢筋混凝土粘结滑移静动态比较试验分析[J].工业建筑,2002,42(S):529-534.

[6]易伟建.混凝土结构试验和理论研究[M].北京:科学出版社,2012:38-46.

[7]Shah,indravadan K.Behavior of bond under dynamic loading[J].ACI Journal Proceedings,1962,19(4):563-584.

[8]Vos E.Influence of loading rate and radial pressure on bond in reinforced concrete-A numerical and experimental approach[M].Delft:Delft University Press,1983.

[9]Cheng Yan.Bond between reinforcing bars and concrete under impact loading[D].The University of British Columbia,1992.

[10]Cheng Y,Sidney M.Bond between epoxy-coated reinforcing bars and concrete under impact loading[J].Canadian Journal of Civil Engineering,1994,21(1):89-100.

[11]洪小健.不同加载速度下锈蚀钢筋与混凝土粘结滑移试验研究[D].上海:同济大学,2001.

[12]洪小健,赵 鸣.加载速率对锈蚀钢筋与混凝土粘结性能的影响[J].同济大学学报,2001,30(7):792-796.

[13]John Henry Weathersby.Investigation of bond slip between concrete and steel reinforcement under dynamic loading conditions[D].Louisiana:Louisiana State University,2003.

[14]Solomos G,Berra M.Rebar pullout testing under dynamic Hopkinson bar induced impulsive loading[J].Materials and Structures,2010,43:247-260.

[15]郑晓燕,吴胜兴.动荷载下锈蚀钢筋混凝土粘结滑移特性的试验研究[J].土木工程学报,2006,39(6):42-46,65.

[16]郑晓燕.锈蚀钢筋与混凝土动态粘结性能研究[D].南京:河海大学,2004.

[17]郑晓燕,吴胜兴,刘龙强.动荷载作用下钢筋与混凝土粘结锚固试验研究[J].混凝土与水泥制品,2001,(6):27-30.

[18]Yan D M,Chen G D.Effect of loading rate on the bonding strength between rebar and concrete[J].Advanced Materials Research,2012,450-451:122-125.

[19]Wei Y,Wu H J,Huang F L.Experimental investigation about dynamic bond-slip between reinforcing steel bar and concrete[J].Applied Mechanics and Materials,2013,249-250:1073-1081.

[20]Alavi-Fard M,Marzouk H.Bond of high strength concrete under monotonic pull-out loading[J].Magazine of Concrete Research,2004,56(9):545-557.

[21]Pacios A,Ouyang C,Shah S P.Rate effect on interfacial response between fibres and matrix[J].Materials and Structures,1995,28:83-91.

[22]Kim D J,El-Tawil S,Naaman,A E.Loading rate effect on pullout behavior of deformed steel fibers[J].ACI Materials Journal (Technical Paper),2008,11/12:576-584.

[23]Bindiganavile V,Banthia N.Impact response of the fiber-matrix bond in concrete[J].Canadian Journal of Civil Engineering,2005,32(5):924-933.

[24]Taher A L,Sameer H,Brian Z.Rate effect on pullout behavior of steel fibers embedded in very-high strength concrete[J].American Journal of Engineering & Applied Sciences,2010,3(2):454-463.

[25]Solomos G,Berra M.Testing of anchorages in concrete under dynamic tensile loading[J].Materials and Structures,2006,39(7):695-706.

[26]李艳茹,刘新宇,汪忠新.爆炸荷载作用下种植钢筋动粘结应力研究[J].防护工程,2004,26(5):9-13.

[27]李艳茹,刘新宇,张 川.爆炸荷载作用下植筋粘结应力有限元分析[J].解放军理工大学学报(自然科学版),2004,5(6):45-48.

[28]刘新宇,李艳茹,王 丹,等.爆炸荷载作用下混合粘结剂植筋的锚固性能试验[J].解放军理工大学学报(自然科学版),2002,3(6):39-42.

[29]Arthur H.Nilson.Internal measurement of bond slip[J].ACI,1972,69(7):439-441.

[30]Mirza S M,Houde J.Study of bond stress-slip relationships in reinforced concrete[J].ACI Structural Journal,1979,76(1):19-46.

[31]Eligehausen R,Popov E P,Bertero V V.Local bond stress-slip relationship of deformed bars under generalized excitations[C].Proceedings of the 7th European Conference on Earthquake Engineering,1982,4:69-80.

[32]徐有邻.变形钢筋-混凝土粘结锚固性能的试验研究[D].北京:清华大学,1990.

[33]Tepfers.Cracking of concrete cover along anchored deformed reinforcing bars[J].Magazine of Concrete Research,1979,31(106):3-12.

[34]高向玲,李 杰.钢筋与混凝土粘结强度的理论计算与试验研究[J].建筑结构,2005,35(4):10-12.

[35]Wang H Z.An analytical study of bond strength associated with splitting of concrete cover[J].Engineering Structures,2009,31(4):968-975.

OverviewofLoadingRateSensitivityoftheBondStress-slipbetweenReinforcingSteelBarsandConcrete

ZHANG Yan-bo

(College of Civil Engineering,Tongji University,Shanghai 200092 PRC)

This article provides a brief summary of a large number of research literature of domestic and foreign about the loading rate sensitivity of bond behavior,systematically introduces and analyzes the research achievements in the field of experimental investigations about dynamic bond behavior.On this basis,with respect to some essential problems in the field of the research of the rate sensitivity of bond behavior,the author puts forward some suggestions on further research and some critical problems that should be paid much more attention to in order to get a better understanding of the effect of loading rate on the bond stress-slip behavior.In addition,this article also introduces three test devices which are widely used in dynamic test to get relatively higher loading rates.

Loading rate,Bond stress-slip,Bond behavior (performance),Rate sensitivity,Test device

2014-02-24;

2014-03-21

张艳波(1987-)，男，河北邯郸人，硕士研究生，研究方向：钢筋混凝土粘结-滑移率敏感性试验研究。

国家自然科学基金项目，国家十二五科技支撑计划项目(2011BAJ09B03-02)。

1001-3679(2014)02-0215-07

TU313

A